tarjan—算法的神(一)
本篇包含 tarjan 求强连通分量、边双连通分量、割点 部分,
tarjan 求点双连通分量、桥(割边)在下一篇。
伟大的 Robert Tarjan 创造了众多被人们所熟知的算法及数据结构,最著名的如:(本文的)连通性相关的 tarjan 算法,Splay-Tree,Toptree,tarjan 求 lca 等等。
注:有向图的强连通分量、无向图的双连通分量、tarjan 求最近公共祖先 被称为 tarjan 三大算法。
所以在本篇博客开篇,%%% Tarjan Dalao.
基础概念:
强连通分量
:
对于一个
有向图
G,存在一个子图使得从该子图中每个点出发都可以到达该子图中任意一点,则称此子图为 G 的强连通分量。特别的,一个点也是一个强连通分量。
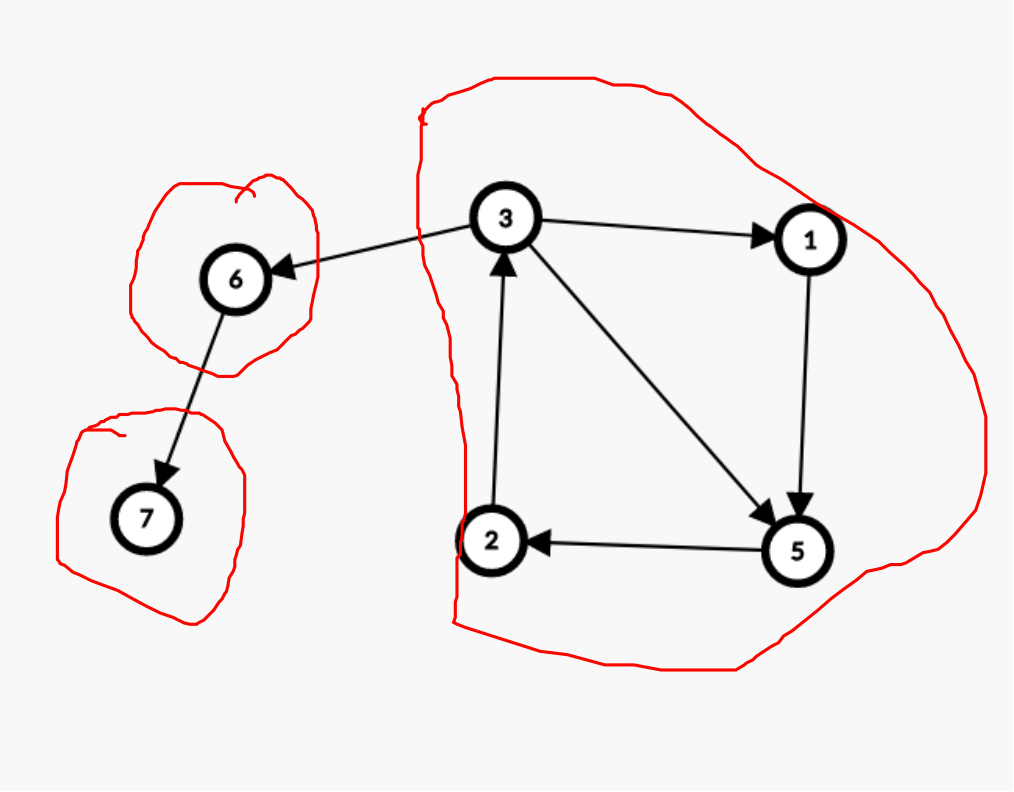
如下图红框部分都是强连通分量:(显然,红框中的点 1、2、3、5 可以互相到达)
割点
:
对于一个
无向连通图
G,若去除 G 中的一个节点 u,并删去与该节点相连的所有边后,G 变得不再连通,则称该点 u 为割点。
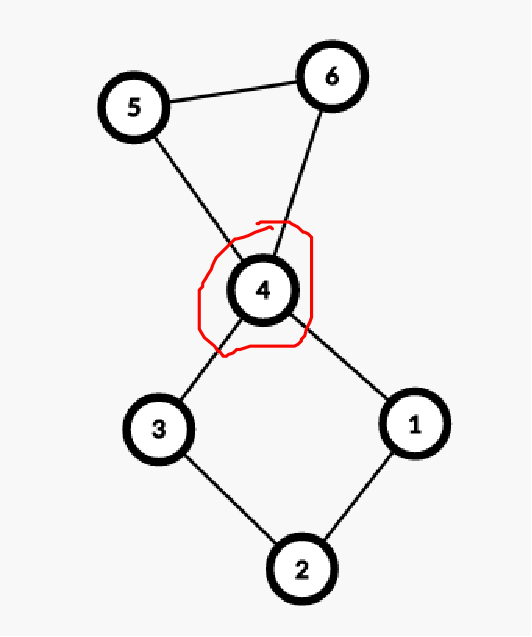
如下图标红的 4 号点就是割点:
割边(桥):
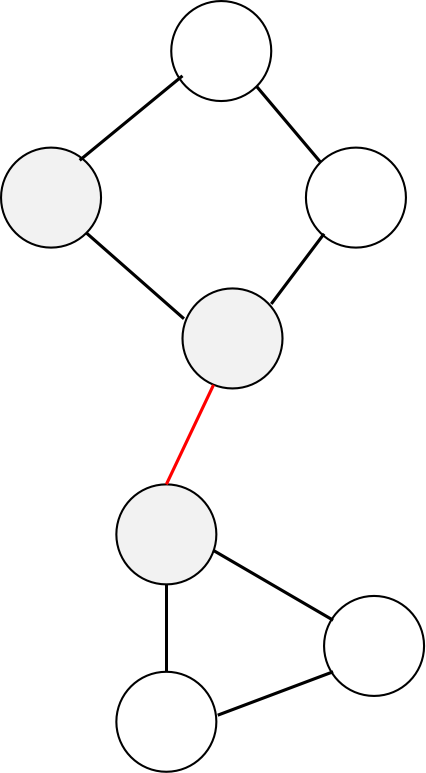
在一个连通分量中,如果删除某一条边,会把这个连通分量分成两个连通分量,那么这个边称为割边(桥)。
如此图中的红边
点/边双连通分量:
若一个
无向图
中的去掉任意一个节点(一条边)都不会改变此图的连通性,即不存在割点(桥),则称作点(边)双连通图。分别简称点双、边双。
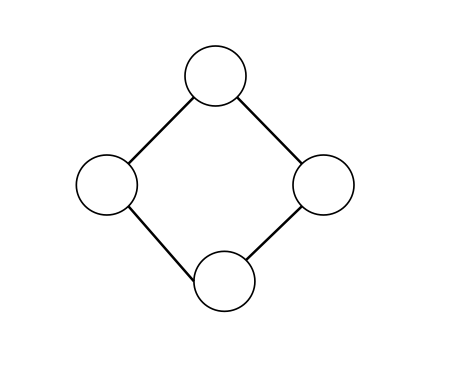
此图既是一个点双又是边双(显然它不含割点也不含桥):
前置知识:
建议先自行了解
dfs 生成树
图片摘自
oi-wiki

邻接链表
存边方式,自行学习(
tarjan 求强连通分量(必看):
需要维护两个数组:
\(dfn_i\)
:表示
\(i\)
这个点的 dfs 序(即深度优先搜索遍历时点
\(i\)
被搜索的次序)
\(low_i\)
:表示从以点
\(i\)
为根节点的子树中任意一点通过一条返祖边能到达的节点的最小值
算法思路:
维护一个栈,存目前正在找的强连通分量的节点。
对图的每个节点进行深度优先搜索,同时维护每个点的
\(low、dfn\)
值,每次搜索到一个点将其加入到栈中。每当找到一个强连通元素(如果一个点的
\(low\)
值和
\(dfn\)
值相等,我们称这个点为强连通元素)时,其实便找全了一个强连通分量。
思路分析(难懂疑问):
- 如何更新
\(low\)
值?
对于搜索过程中搜到的的点
\(u\)
和它连向的点
\(v\)
,有以下三种情况:
1 . 点
\(v\)
还未被访问:此时我们继续对
\(v\)
进行搜索。在回溯过程中用
\(low_v\)
更新
\(low_u\)
。 因为
\(v\)
的子树中的点其实也就是
\(u\)
的子树中点,那么
\(v\)
子树中一个点能到达
\(x\)
点,即为
\(u\)
子树中的点到达了
\(x\)
点。
2 . 点
\(v\)
被访问过并且已经在栈中:(即在当前强连通分量中),被访问过说明
\(v\)
在搜索树中是
\(u\)
的祖先节点,那么从
\(u\)
走到
\(v\)
的边便是我们更新
\(low\)
要用的那条返祖边,所以用
\(dfn_v\)
值更新
\(low_u\)
;
3 . 点
\(v\)
被访问过但不在栈中:说明该点所在强连通分量已经被找到了,且该点不在现在正找的强连通分量里,那么不用进行操作。
- 为什么找到强联通元素的时候当前的就找全了一个强连通分量呢?
我们知道强联通元素
\(x\)
有
\(low_x = dfn_x\)
,说明以
\(x\)
为根的子树中所有点都到达不了
\(x\)
之前的(同一强连通分量中的)点,那么
\(x\)
便是该强连通分量的“起点”。
根据栈先进后出的性质,可以知道栈中从
\(x\)
到栈顶的点都是
\(x\)
子树内的点,并且是和
\(x\)
属于同一个强连通分量的。那么找到
\(x\)
这个强连通元素后,栈中从
\(x\)
到栈顶所有点(这些点是当前的强连通分量中的点)取出即可。
伪代码:
tarjan(点 x){
low[x] = dfn[x] = ++th; // 更新 dfs 序
把 x 入栈;
for(枚举 x 相邻的点 y){
if(y 未被搜索过){
tarjan(y);
low[x] = min(low[x], low[y]);
}
if(y 被搜索过且已在栈中){
low[x] = min(low[x], dfn[y]);
}
}
if(x 为强连通元素){
scc++; //scc 为强连通分量个数
将栈中元素从 x 到栈顶依次取出;
}
}
算法演示:
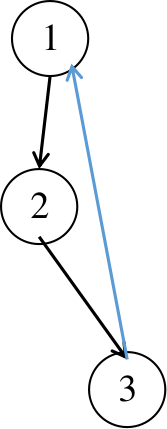
黑边为
树边
,蓝边为
返祖边
;
在此连通图中,我们以 1 号点为根进行 dfs,所有点的标号即为它们的 dfs 序:
我们从 1 开始 dfs,把 1 加进栈中,找到 1 相邻的点 2,发现 2 还未被搜索过,那么递归 dfs 2;
把 2 加进栈中,找到与 2 相邻的点 3,3 同样未被搜索,再递归搜索 3;
同样把 3 加进栈中,发现 3 相邻的点 1 已经被搜索过且在已在栈中,那么从 3 到 1 这条边就是一条返祖边,用
\(dfn_1\)
更新
\(low_3\)
,回溯;
回溯过程中,分别用
\(low_3\)
更新
\(low_2\)
,
\(low_2\)
更新
\(low_1\)
。
回溯到 1 号节点时,有
\(low_1 = dfn_1\)
,所以 1 号节点为强连通元素,那么栈中从 1 到栈顶所有元素即为一个强连通分量。
算法代码:
int th, top, scc; //分别表示 dfs 的时间戳、栈顶、强连通分量个数
int s[N], ins[N]; //s 为手写栈,ins[i] 表示 i 这个点是否在栈中
int low[N], dfn[N], belong[N]; //belong[i] 表示 i 这个点所属的强连通分量的标号
void tarjan(int x){
low[x] = dfn[x] = ++th;
s[++top] = x, ins[x] = true;
for(int i=head[x]; i; i=nxt[i]){ //链式前向星存边
int y = to[i];
if(!dfn[y]){ //若 y 还没被搜索过
tarjan(y); // 搜索 y
low[x] = min(low[x], low[y]);
}
else if(ins[y]){ // y 在栈中
low[x] = min(low[x], dfn[y]);
}
}
if(low[x] == dfn[x]){
++scc;
do{ //将栈中从 x 到栈顶所有元素取出
belong[s[top]] = scc;
ins[s[top]] = false;
}while(s[top--] != y);
}
}
但是,大多数题目并不是给定一张联通图,所以一张图可能会分成多个强连通分量,所以主函数中应这样写(来保证每个强连通分量都被跑过 tarjan):
for(int i=1; i<=n; i++)
if(!dfn[i]) tarjan(i);
例题:
不要着急看下面的内容,建议做一两道例题熟悉算法原理和代码后再继续学习。
The Cow Prom S[USACO06JAN]
(绝对的板子)
板!
信息传递[NOIP2015 提高组]
特殊的最小环问题,因为这个题保证每个点的出度为 1,所以这个题可以用 tarjan 求强连通分量来做,具体可以去看其他题解(
比如这个
)。
受欢迎的牛[USACO03FALL / HAOI2006]
缩点的思想,但很好理解,求出强联通分量,把每个强连通分量看做一个大点,计算每个大点的出度,若有一个出度为 0 的大点,则这个大点包含的所有奶牛都为明星牛;若有两个及以上出度为 0 的大点(则这些大点里的爱慕都无法传播出去)就 G 了,便不存在明星牛。
具体实现看代码吧
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m, out[N];
int low[N], dfn[N], ins[N], th;
int s[N], belong[N], top, scc, size[N];
int head[N], to[N], nxt[N], tot;
void addedge(int x, int y){
to[++tot] = y;
nxt[tot] = head[x];
head[x] = tot;
}
void tarjan(int x){
low[x] = dfn[x] = ++th;
s[++top] = x, ins[x] = true;
for(int i=head[x]; i; i=nxt[i]){
int y = to[i];
if(!dfn[y]){
tarjan(y);
low[x] = min(low[x], low[y]);
}
else if(ins[y]){
low[x] = min(low[x], dfn[y]);
}
}
if(low[x] == dfn[x]){
++scc;
do{
size[scc]++;
belong[s[top]] = scc;
ins[s[top]] = false;
}while(s[top--] != x);
}
}
int main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin>>n>>m;
for(int i=1; i<=m; i++){
int x, y; cin>>x>>y;
addedge(x, y);
}
for(int i=1; i<=n; i++){
if(!dfn[i]) tarjan(i);
}
for(int i=1; i<=n; i++){
for(int j=head[i]; j; j=nxt[j]){
int y = to[j];
if(belong[i] != belong[y]) out[belong[i]]++;
}
}
int cnt = 0, ans = 0;
for(int i=1; i<=scc; i++){
if(out[i]) continue;
cnt++;
if(cnt > 1){cout<<0; return 0;}
ans = size[i];
}
cout<<ans;
return 0;
}
tarjan 求边双连通分量
有一种实现是先跑出割桥再找边双,本篇不对此方法进行介绍。
其实我们可以发现边双连通分量就是强连通分量搞到无向图中,求边双的思路也和强连通分量一样。(看代码理解即可,非常简单)
和强连通分量的不同之处在代码中标出了。
算法代码:
void tarjan(int x, int p){
low[x] = dfn[x] = ++th;
s[++top] = x, ins[x] = true;
for(int i=head[x]; i; i=nxt[i]){
int y = to[i];
if(y == p) continue;//因为双向边所以搜索时加个判父亲节点
if(!dfn[y]){
tarjan(y, x);
low[x] = min(low[x], low[y]);
}
else low[x] = min(low[x], dfn[y]);
//因为在无向图中,所以若 y 已经被搜索过则一定是 x 的祖先,不用再判 ins
}
if(dfn[x] == low[x]){
++scc;
do{
belong[s[top]] = scc;
SCC[scc].emplace_back(s[top]); //将边双存起来,可根据题目需要选择写这句话
}while(s[top--] != x);
}
}
但注意题目要求,有时题目可能会有重边时,搜索过程中就不能只特判父亲节点,而是应该记一下边的编号判边。因为有重边的话是可以回到父亲节点的。
例题:
【模板】边双联通分量
板子题,但注意题目可能会有重边,所以需要记一下边防止走“回头路”。
看代码就知道了
#include <bits/stdc++.h>
using namespace std;
const int N = 5e6 + 10;
int n, m, top, th, cnt;
int s[N], low[N], dfn[N], id[N];
int tot, head[N], to[N], nxt[N];
vector<vector<int> >ans;
inline void addedge(int x, int y){
to[++tot] = y;
nxt[tot] = head[x];
head[x] = tot;
id[tot] = cnt; //id 来记一下边的编号
}
inline void tarjan(int x, int p){
low[x] = dfn[x] = ++th;
s[++top] = x;
for(int i=head[x]; i; i=nxt[i]){
int y(to[i]), edge = id[i];
if(edge == p) continue; //解决重边问题
if(!dfn[y]){
tarjan(y, edge);
low[x] = min(low[x], low[y]);
}
else low[x] = min(low[x], dfn[y]);
}
if(low[x] == dfn[x]){
vector<int>scc;
do scc.emplace_back(s[top]);
while(s[top--] != x);
ans.emplace_back(scc);
}
}
int main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin>>n>>m;
for(int i=1; i<=m; i++){
int x, y; cin>>x>>y;
if(x == y) continue; ++cnt;
addedge(x, y), addedge(y, x);
}
for(int i=1; i<=n; i++)
if(!dfn[i]) tarjan(i, 0);
cout<<ans.size()<<"\n";
for(auto x : ans){
cout<<x.size()<<" ";
for(auto i : x){
cout<<i<<" ";
}
cout<<"\n";
}
return 0;
}