2023年3月

屎上最全vue-pdf+Springboot与aspose-words整合，开箱即用

作者: wenmo8
时间: 2023-03-21
分类: 其它
评论

前言

⏲️本文阅读时长：约10分钟

刷爆 LeetCode 双周赛 100，单方面宣布第一题最难

作者: wenmo8
时间: 2023-03-21
分类: 其它
评论

本文已收录到
AndroidFamily
，技术和职场问题，请关注公众号 [彭旭锐] 提问。

大家好，我是小彭。

上周末是 LeetCode 第 100 场双周赛，你参加了吗？这场周赛整体没有 Hard 题，但是也没有 Easy 题。第一题国服前百名里超过一半人 wa，很少见。

小彭的技术交流群 02 群来了，公众号回复 “加群” 加入我们~

周赛概览

2591. 将钱分给最多的儿童（Easy）
- 题解一：模拟 $O(1)$
- 题解二：完全背包 $O(children·money^2)$
2592. 最大化数组的伟大值（Medium）
- 题解一：贪心 / 田忌赛马 $O(nlgn)$
- 题解二：最大重复计数 $O(n)$
2593. 标记所有元素后数组的分数（Medium）
- 题解一：排序 O$(nlgn)$
- 题解二：按照严格递减字段分组 $O(n)$
2594. 修车的最少时间（Medium)
- 题解一：二分查找 $O(n + U·log(mc^2))$
- 题解二：二分查找 + 计数优化 $O(n·log(mc^2))$

2591. 将钱分给最多的儿童（Easy）

题目地址

https://leetcode.cn/problems/distribute-money-to-maximum-children/description/

题目描述

给你一个整数
money
，表示你总共有的钱数（单位为美元）和另一个整数
children
，表示你要将钱分配给多少个儿童。

你需要按照如下规则分配：

所有的钱都必须被分配。
每个儿童至少获得
1
美元。
没有人获得
4
美元。

请你按照上述规则分配金钱，并返回
最多
有多少个儿童获得
恰好
**
8
美元。如果没有任何分配方案，返回
-1
。

题解一（模拟）

这道题搞数字迷信？发发发 888？

简单模拟题，但是错误率很高，提交通过率仅 19%。

class Solution {
    fun distMoney(money: Int, children: Int): Int {
        var left = money
        // 每人至少分配 1 元
        left -= children
        // 违反规则 2
        if (left < 0) return -1
        // 1、完美：正好所有人可以分配 8 元
        if (left == children * 7) return children
        // 2、溢出：所有人可以分配 8 元有结余，需要选择 1 个人分配结余的金额
        if (left > children * 7) return children - 1
        // 3、不足：尽可能分配 8 元
        var sum = left / 7
        // 结余金额
        left -= sum * 7
        // 如果结余 3 元，并且剩下 1 人分配了 1 元，需要破坏一个 8 元避免出现分配 4 美元
        if (left == 3 && children - sum == 1) return sum - 1
        return sum
    }
}

复杂度分析：

时间复杂度：$O(1)$
空间复杂度：$O(1)$

题解二（完全背包问题）

竞赛中脑海闪现过背包问题的思路，但第一题暴力才是王道，赛后验证可行。

包裹：最多有
children
人；
物品：每个金币价值为 1 且不可分割，最多物品数为
money
个；
目标：包裹价值恰好为 8 的最大个数；
限制条件：不允许包裹价值为 4，每个包裹至少装 1 枚金币。

令
dp[i][j]
表示分配到
i
个人为止，且分配总金额为
j
元时的最大价值，则有：

递推关系：

$$
dp[i][j]=\sum_{k=1}^{j,k!=4} dp[i-1][j-k] + I(k==8)
$$

初始状态
dp[0][0] = 0
终止状态
dp[children][money]

class Solution {
    fun distMoney(money: Int, children: Int): Int {
        var left = money
        // 每人至少分配 1 元
        left -= children
        // 违反规则 2
        if (left < 0) return -1
        val dp = Array(children + 1) { IntArray(left + 1) { -1 } }
        dp[0][0] = 0
        // i：枚举包裹
        for (i in 1..children) {
            // j：枚举金额
            for (j in 0..left) {
                // k：枚举选项
                for (k in 0..j) {
                    // 不允许选择 3
                    if (k == 3) continue
                    // 子状态违反规则
                    if (-1 == dp[i - 1][j - k]) continue
                    // 子状态 + 当前包裹状态
                    val cnt = dp[i - 1][j - k] + if (k == 7) 1 else 0
                    dp[i][j] = Math.max(dp[i][j], cnt)
                }
            }
        }
        return dp[children][left]
    }
}

滚动数组优化：

class Solution {
    fun distMoney(money: Int, children: Int): Int {
        var left = money
        // 每人至少分配 1 元
        left -= children
        // 违反规则 2
        if (left < 0) return -1
        val dp = IntArray(left + 1) { -1 }
        dp[0] = 0
        // i：枚举包裹
        for (i in 1..children) {
            // j：枚举金额
            for (j in left downTo 0) {
                // k：枚举选项
                for (k in 0..j) {
                    // 不允许选择 3
                    if (k == 3) continue
                    // 子状态违反规则
                    if (-1 == dp[j - k]) continue
                    // 子状态 + 当前包裹状态
                    val cnt = dp[j - k] + if (k == 7) 1 else 0
                    dp[j] = Math.max(dp[j], cnt)
                }
            }
        }
        return dp[left]
    }

复杂度分析：

时间复杂度：$O(children·money^2)$
空间复杂度：$O(money)$

近期周赛背包问题：

2592. 最大化数组的伟大值（Medium）

题目地址

https://leetcode.cn/problems/maximize-greatness-of-an-array/

题目描述

给你一个下标从 0 开始的整数数组
nums
。你需要将
nums
重新排列成一个新的数组
perm
。

定义
nums
的
伟大值
为满足
0 <= i < nums.length
且
perm[i] > nums[i]
的下标数目。

请你返回重新排列
nums
后的
最大
伟大值。

题解一（贪心 / 田忌赛马）

贪心思路：田忌赛马，以下赛马策略最优：

田忌的中等马对齐威王的下等马，田忌胜；
田忌的上等马对齐威王的中等马，田忌胜；
田忌的下等马对齐威王的下等马，齐威王胜。

回到本题，考虑一组贡献伟大值的配对 $(p, q)$，其中 $p < q$。由于越小的值越匹配到更大值，为了让结果最优，应该让 p 尽可能小，即优先匹配 nums 数组的较小值。那么 $q$ 如何选择呢？有 2 种策略：

策略 1 - 优先匹配最大值：无法得到最优解，因为会消耗了较大的 q 值，可能导致部分 p 值无法匹配（如果田忌用上等马对齐威王的下等马，最终将是齐威王生出）；
策略 2- 优先匹配最接近的更大值：最优解，即田忌赛马策略，以 [1,1,1,2,3,3,5] 为例：
- 初始状态 i = 0，j = 0；
- i = 0，j = 0，无法贡献伟大值，j 自增 1（寻找最接近的更大值）；
- i = 0，j = 1，无法贡献伟大值，j 自增 1；
- i = 0，j = 2，无法贡献伟大值，j 自增 1；
- i = 0，j = 3，贡献伟大值，j 自增 1，i 自增 1；
- i = 1，j = 4，贡献伟大值，j 自增 1，i 自增 1；
- i = 2，j = 5，贡献伟大值，j 自增 1，i 自增 1；
- i = 3，j = 6，贡献伟大值，j 自增 1，i 自增 1；
- 退出循环，i = 4；正好等于伟大值 4。

class Solution {
    fun maximizeGreatness(nums: IntArray): Int {
        nums.sort()
        // i：参与匹配的指针
        var i = 0
        for (num in nums) {
            // 贡献伟大值
            if (num > nums[i]) i++
        }
        return i
    }
}

复杂度分析：

时间复杂度：$O(nlgn + n)$ 排序 + 线性遍历，其中 $n$ 是 $nums$ 数组长度；
空间复杂度：$O(lgn)$ 排序递归栈空间。

题解二（最大重复计数）

竞赛中从测试用例中观察到题解与最大重复数存在关系，例如：

用例 [1,1,1,2,3,3,5]：最大重复数为 3，一个最优方案为 [2,3,3,5,x,x,x]，最大伟大值为 7 - 3 = 4，其中 7 是数组长度；
用例 [1,2,2,2,2,3,5]：最大重复数为 4，一个最优方案为 [2,3,5,x,x,x,x]，最大伟大值为 7 - 4 = 3，其中 7 是数组长度；
用例 [1,1,2,2,2,2,3,3,5]，最大重复数为 4，一个最优方案为 [2,2,3,3,5,x,x,x,x]，最大伟大值为 9 - 4 = 5，其中 9 是数组长度。

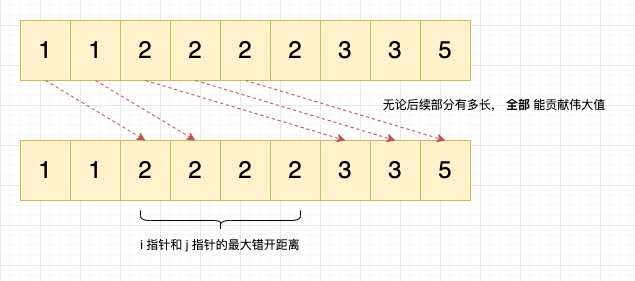
我们发现题目的瓶颈在于数字最大重复出现计数。最大伟大值正好等于
数组长度 - 最大重复计数。

如何证明？关键在于 i 指针和 j 指针的最大距离：

当 i 指针指向重复元素的首个元素时（例如下标为 0、2、6 的位置），j 指针必须移动到最接近的较大元素（例如下标为 2，6，8 的位置）。而 i 指针和 j 指针的最大错开距离取决于数组重复出现次数最多的元素，只要错开这个距离，无论数组后续部分有多长，都能够匹配上。

class Solution {
    fun maximizeGreatness(nums: IntArray): Int {
        var maxCnt = 0
        val cnts = HashMap<Int, Int>()
        for (num in nums) {
            cnts[num] = cnts.getOrDefault(num, 0) + 1
            maxCnt = Math.max(maxCnt, cnts[num]!!)
        }
        return nums.size - maxCnt
    }
}

复杂度分析：

时间复杂度：$O(n)$ 其中 $n$ 是 $nums$ 数组的长度；
空间复杂度：$O(n)$ 其中 $n$ 是 $cnts$ 散列表空间。

2593. 标记所有元素后数组的分数（Medium）

题目地址

https://leetcode.cn/problems/find-score-of-an-array-after-marking-all-elements/

题目描述

给你一个数组
nums
，它包含若干正整数。

一开始分数
score = 0
，请你按照下面算法求出最后分数：

从数组中选择最小且没有被标记的整数。如果有相等元素，选择下标最小的一个。
将选中的整数加到
score
中。
标记
被选中元素
，如果有相邻元素，则同时标记
与它相邻的两个元素
。
重复此过程直到数组中所有元素都被标记。

请你返回执行上述算法后最后的分数。

题解一（排序）

这道题犯了大忌，没有正确理解题意。一开始以为 “相邻的元素” 是指未标记的最相邻元素，花了很多时间思考如何快速找到左右未标记的数。其实题目没有这么复杂，就是标记数组上的相邻元素。

如此这道题只能算 Medium 偏 Easy 难度。

class Solution {
    fun findScore(nums: IntArray): Long {
        // 小顶堆（索引）
        val heap = PriorityQueue<Int>() { i1, i2 ->
            if (nums[i1] != nums[i2]) nums[i1] - nums[i2] else i1 - i2
        }.apply {
            for (index in nums.indices) {
                offer(index)
            }
        }
        var sum = 0L
        while (!heap.isEmpty()) {
            val index = heap.poll()
            if (nums[index] == 0) continue
            // 标记
            sum += nums[index]
            nums[index] = 0
            // 标记相邻元素
            if (index > 0) nums[index - 1] = 0
            if (index < nums.size - 1) nums[index + 1] = 0
        }
        return sum
    }
}

复杂度分析：

时间复杂度：$O(nlgn)$ 堆排序时间，其中 $n$ 是 $nums$ 数组长度；
空间复杂度：$O(n)$ 堆空间。

题解二（按照严格递减字段分组）

思路参考：
灵茶山艾府的题解

按照严格递减字段分组，在找到坡底后间隔累加 nums[i]，nums[i - 2]，nums[i - 4]，并从 i + 2 开始继续寻找坡底。

class Solution {
    fun findScore(nums: IntArray): Long {
        val n = nums.size
        var sum = 0L
        var i = 0
        while (i < nums.size) {
            val i0 = i // 坡顶
            while (i + 1 < n && nums[i] > nums[i + 1]) i++ // 寻找坡底
            for (j in i downTo i0 step 2) { // 间隔累加
                sum += nums[j]
            }
            i += 2 // i + 1 不能选
        }
        return sum
    }
}

复杂度分析：

时间复杂度：$O(n)$ 其中 $n$ 是 $nums$ 数组的长度，每个元素最多访问 2 次；
空间复杂度：$O(1)$ 只使用常数空间。

2594. 修车的最少时间（Medium)

题目地址

https://leetcode.cn/problems/minimum-time-to-repair-cars/

题目描述

给你一个整数数组
ranks
，表示一些机械工的
能力值
。
ranksi
是第
i
位机械工的能力值。能力值为
r
的机械工可以在
r * n2
分钟内修好
n
辆车。

同时给你一个整数
cars
，表示总共需要修理的汽车数目。

请你返回修理所有汽车
最少
需要多少时间。

注意：
所有机械工可以同时修理汽车。

题解（二分查找）

我们发现问题在时间 t 上存在单调性：

假设可以在 t 时间内修完所有车，那么大于 t 的时间都能修完；
如果不能在 t 时间内修完所有车，那么小于 t 的时间都无法修完。

因此，我们可以用二分查找寻找 “可以修完的最小时间”：

二分的下界：1；
二分的上界：将所有的车交给能力值排序最高的工人，因为他的效率最高。

class Solution {
    fun repairCars(ranks: IntArray, cars: Int): Long {
        // 寻找能力值排序最高的工人
        var minRank = Integer.MAX_VALUE
        for (rank in ranks) {
            minRank = Math.min(minRank, rank)
        }
        var left = 1L
        var right = 1L * minRank * cars * cars
        // 二分查找
        while (left < right) {
            val mid = (left + right) ushr 1
            if (check(ranks, cars, mid)) {
                right = mid
            } else {
                left = mid + 1
            }
        }
        return left
    }

    // return 能否在 t 时间内修完所有车
    private fun check(ranks: IntArray, cars: Int, t: Long): Boolean {
        // 计算并行修车 t 时间能修完的车（由于 t 的上界较大，carSum 会溢出 Int）
        var carSum = 0L
        for (rank in ranks) {
            carSum += Math.sqrt(1.0 * t / rank).toLong()
        }
        return carSum >= cars
    }
}

复杂度分析：

时间复杂度：$O(n·log(mc^2))$ 其中 $n$ 是 $ranks$ 数组长度，$m$ 是 $ranks$ 数组的最小值，$c$ 是车辆数量，二分的次数是 $O(log(mc^2))$，每次 $check$ 操作花费 $O(n)$ 时间；
空间复杂度：$O(1)$ 仅使用常量级别空间。

题解二（二分查找 + 计数优化）

我们发现 $ranks$ 的取值范围很小，所有可以用计数优化每次 $check$ 操作的时间复杂度：

class Solution {
    fun repairCars(ranks: IntArray, cars: Int): Long {
        // 寻找能力值排序最高的工人
        val cnts = IntArray(101)
        var minRank = Integer.MAX_VALUE
        for (rank in ranks) {
            minRank = Math.min(minRank, rank)
            cnts[rank]++
        }
        var left = 1L
        var right = 1L * minRank * cars * cars
        // 二分查找
        while (left < right) {
            val mid = (left + right) ushr 1
            if (check(ranks, cars, cnts, minRank, mid)) {
                right = mid
            } else {
                left = mid + 1
            }
        }
        return left
    }

    // return 能否在 t 时间内修完所有车
    private fun check(ranks: IntArray, cars: Int, cnts: IntArray, minRank: Int, t: Long): Boolean {
        // 计算并行修车 t 时间能修完的车（由于 t 的上界较大，carSum 会溢出 Int）
        var carSum = 0L
        for (rank in minRank..100) {
            if (cnts[rank] == 0) continue
            carSum += cnts[rank] * Math.sqrt(1.0 * t / rank).toLong()
        }
        return carSum >= cars
    }
}

复杂度分析：

时间复杂度：$O(n + U·log(mc^2))$ 其中 $n$ 是 $ranks$ 数组长度，$m$ 是 $ranks$ 数组的最小值，$U$ 是 $ranks$ 数组的取值范围，$c$ 是车辆数量，二分的次数是 $O(log(mc^2))$，每次 $check$ 操作花费 $O(U)$ 时间；
空间复杂度：$O(U)$ $cnts$ 计数数组空间。

近期周赛二分查找题目：

这场周赛就这么多，我们下周见。

【单元测试】Junit 4（八）--junit4 内置Rule

作者: wenmo8
时间: 2023-03-21
分类: 其它
评论

1.0 Rules

Rules允许非常灵活地添加或重新定义一个测试类中每个测试方法的行为。测试人员可以重复使用或扩展下面提供的Rules之一，或编写自己的Rules。

1.1 TestName

TestName Rule使当前的测试名称在测试方法中可用。用于在测试执行过程中获取测试方法名称。在starting()中记录测试方法名，在getMethodName()中返回

例如：

import static org.junit.Assert.*;

import org.junit.Rule;
import org.junit.Test;
import org.junit.rules.TestName;

public class NameRuleTest {
  @Rule
  public final TestName name = new TestName();
  
  @Test
  public void testA() {
    assertEquals("testA", name.getMethodName());
  }
  
  @Test
  public void testB() {
    assertEquals("testB", name.getMethodName());
  }
}

1.2 TemporaryFolder

TemporaryFolder Rule允许创建文件和文件夹，这些文件和文件夹在
测试方法结束时被删除
（无论通过还是失败）。默认情况下，如果资源不能被删除，则不会抛出异常。

import java.io.*;

import org.junit.Rule;
import org.junit.Test;
import org.junit.rules.TemporaryFolder;

public class HasTempFolder {
        @Rule
        public TemporaryFolder folder= new TemporaryFolder();

        @Test
        public void testUsingTempFolder() throws IOException {
                File createdFile = folder.newFile("myfile.txt");
                File createdFolder = folder.newFolder("subfolder");
                // ...
        }
 }

TemporaryFolder#newFolder(String... folderNames)可以根据输入的参数创建目录。如果是多级目录，可以递归创建。
TemporaryFolder#newFile()可以创建一个随机名字的临时文件；
TemporaryFolder##newFolder() 可以创建一个随机名字的临时目录。

1.3
ExternalResource

ExternalResource是一个规则（如TemporaryFolder）的基类，它在测试前设置了一个外部资源（一个文件、套接字、服务器、数据库连接等），并保证在测试后将其拆除。

可以设置测试前后需要做的事情（比如：文件、socket、服务、数据库的连接与关闭）。

 public static class UsesExternalResource {
   Server myServer = new Server();
 
   @Rule
   public ExternalResource resource = new ExternalResource() {
     @Override
     protected void before() throws Throwable {
       myServer.connect();
     };
 
     @Override
     protected void after() {
       myServer.disconnect();
     };
   };
 
   @Test
   public void testFoo() {
     new Client().run(myServer);
   }
 }

ExternalResource#before会在每个测试之前处理；#after会在每个测试之后处理；
关于ExternalResource与@Before已经@After等标记步骤的执行顺序，我们会在本文后面部分介绍。

1.4
ErrorCollector

ErrorCollector这个Rule，在出现一个错误后，还可以让测试继续进行下去。

他提供三个方法：

checkThat(final T value, Matcher
matcher)
checkSucceeds(Callable
addError(Throwable error)

前面两个是用来处理断言的，最后一个是添加错误至错误列表中。

看下面例子：

 package mytest;
 
 import static org.hamcrest.CoreMatchers.is;
 import static org.junit.Assert.assertThat;
 
 import java.util.concurrent.Callable;
 
 import org.junit.Rule;
 import org.junit.Test;
 import org.junit.rules.ErrorCollector;
 
 public class JUnitCoreErrorControllerRuleTest {
 
   private final int multiplesOf2[] = { 0, 2, 4, 7, 8, 11, 12 };
 
   @Rule
   public ErrorCollector errorCollector = new ErrorCollector();
 
   /*
    * 下面这个测试，会报告两个failures。这一点和下面的checkSucceeds测试不同
    */
   @Test
   public void testMultiplesOf2() {
     int multiple = 0;
     for (int multipleOf2 : multiplesOf2) {
       // Will count the number of issues in this list
       // - 3*2 = 6 not 7, 5*2 = 10 not 11 : 2 Failures
       errorCollector.checkThat(2 * multiple, is(multipleOf2));
       multiple++;
     }
   }
 
   /*
    * 下面代码中有两个断言会失败，但每次运行JUnit框架只会报告一个。这一点和上面的checkThat测试不同，可以对比一下。
    */
   @Test
   public void testCallableMultiples() {
     errorCollector.checkSucceeds(new Callable<Object>() {
       public Object call() throws Exception {
         assertThat(2 * 2, is(5));
         assertThat(2 * 3, is(6));
         assertThat(2 * 4, is(8));
         assertThat(2 * 5, is(9));
         return null;
       }
     });
   }
 
   /*
    * 下面运行时，会报告2个错误
    */
   @Test
   public void testAddingAnError() {
     assertThat(2 * 2, is(4));
     errorCollector.addError(new Throwable("Error Collector added an error"));
     assertThat(2 * 3, is(6));
     errorCollector.addError(new Throwable(
         "Error Collector added a second error"));
   }
 
 }

运行结果：

 Failed tests: 
 
 testCallableMultiples(mytest.JUnitCoreErrorControllerRuleTest): 
 Expected: is <5>
     but: was <4>
 
 testMultiplesOf2(mytest.JUnitCoreErrorControllerRuleTest): 
 Expected: is <7>
     but: was <6>
 
 testMultiplesOf2(mytest.JUnitCoreErrorControllerRuleTest): 
 Expected: is <11>
     but: was <10>
 
 Tests in error: 
 testAddingAnError(tangzhi.mytest.JUnitCoreErrorControllerRuleTest): Error Collector added an error
 
 testAddingAnError(tangzhi.mytest.JUnitCoreErrorControllerRuleTest): Error Collector added a second error

从这个例子，可以看出：

ErrorCollector#checkThat 会报告测试中的每一个failures
ErrorCollector#checkSucceeds 只会检查是否成功，如果不成功，只报告第一个导致不成功的failure
ErrorCollector#addError 是添加一个错误(error)。

1.5
Verifier

如果，你想在每个测试之后，甚至是在@After之后，想检查些什么，就可以使用Verifier这个Rule.

看例子：

 private static String sequence;
 
 public static class UsesVerifier {
   @Rule
   public Verifier collector = new Verifier() {
       @Override
       protected void verify() {
           sequence += " verify ";
       }
   };
 
   @Test
   public void example() {
       sequence += "test";
   }
 
   @Test
   public void example2() {
       sequence += "test2";
   }
 
   @After
   public void after() {
       sequence += " after";
   }
 }
 
 @Test
 public void verifierRunsAfterTest() {
   sequence = "";
   assertThat(testResult(UsesVerifier.class), isSuccessful());
   assertEquals("test after verify test2 after verify ", sequence);
 }

从上面例子可以看出:Verifier#verify针对每个测试都会运行一次，并且运行在@After步骤之后。

需要说明：如果某测试出现失败(fail)，那么这个测试之后就不会做verify,这一点，可以结合下面的例子看出

1.6
TestWatcher

对测试的每个步骤进行监控。

看例子：

 package tangzhi.mytest;
 
 import static org.junit.Assert.*;  
 import static org.hamcrest.CoreMatchers.*;
 
 import org.junit.After;
 import org.junit.Rule;
 import org.junit.Test;
 import org.junit.rules.TestRule;
 import org.junit.rules.TestWatcher;
 import org.junit.rules.Verifier;
 import org.junit.runner.Description;
 import org.junit.runners.model.Statement;
 
 public class WatchmanTest {
     private static String watchedLog;
 
       @Rule
       public TestRule watchman = new TestWatcher() {
         @Override
         public Statement apply(Statement base, Description description) {
             Statement s = super.apply(base, description);
             watchedLog="";
             System.out.println("watch apply.");
             return s;
         }
 
         @Override
         protected void succeeded(Description description) {
             watchedLog += description.getDisplayName() + " " + "success!";
             System.out.println("watch succeed:"+watchedLog);
 
         }
 
         @Override
         protected void failed(Throwable e, Description description) {
             watchedLog += description.getDisplayName() + " " + e.getClass().getSimpleName();
             System.out.println("watch failed:"+watchedLog);
 
         }
 
         @Override
         protected void starting(Description description) {
           super.starting(description);
           System.out.println("watch starting.");
         }
 
         @Override
         protected void finished(Description description) {
           super.finished(description);
           System.out.println("watch finished.");
         }
       };
 
       @Rule
       public Verifier collector = new Verifier() {
           @Override
           protected void verify() {
               System.out.println("@Verify:"+watchedLog);
           }
       };
 
       @Test
       public void fails() {
           System.out.println("in fails");
           assertThat("ssss", is("sss"));
       }
 
       @Test
       public void succeeds() {
           System.out.println("in succeeds");
       }
 
       @After
       public void after() {
           System.out.println("@After");
       }
 }

1.7
Timeout

对于添加了TimeoutRule 的测试类，当测试类中的测试方法执行超过TimeoutRule 配置的时间时，测试方法执行就会被标记为失败

public class TimeoutRuleTest {
	@Rule
	public Timeout globalTimeout = Timeout.seconds(5);
	 
	@Test
	public void timeout() throws InterruptedException {
	    TimeUnit.SECONDS.sleep(10);
	}

	@Test
	public void onTime() throws InterruptedException {
		TimeUnit.SECONDS.sleep(2);
	}
	
}

执行上面测试用例，onTime方法执行通过，timeout()方法则抛出TestTimedOutException：

org.junit.runners.model.TestTimedOutException: test timed out after 5 seconds

还有很多Rule就不一一介绍了

【开源】最近写了一个简单的网址导航网站

作者: wenmo8
时间: 2023-03-21
分类: 其它
评论

前言

随着团队的成长，要管理的项目或使用的内部系统越来越多，很多内部系统都没有域名，使用IP+端口，很难记。

为了解决这个痛点，我抽空写了个导航网站~ 目前用下来效果还不错，可以基本完美的解决这个问题。

项目名称是
SiteDirectory
，代码在 Github 开源了:
https://github.com/Deali-Axy/SiteDirectory

SiteDirectory 网站导航