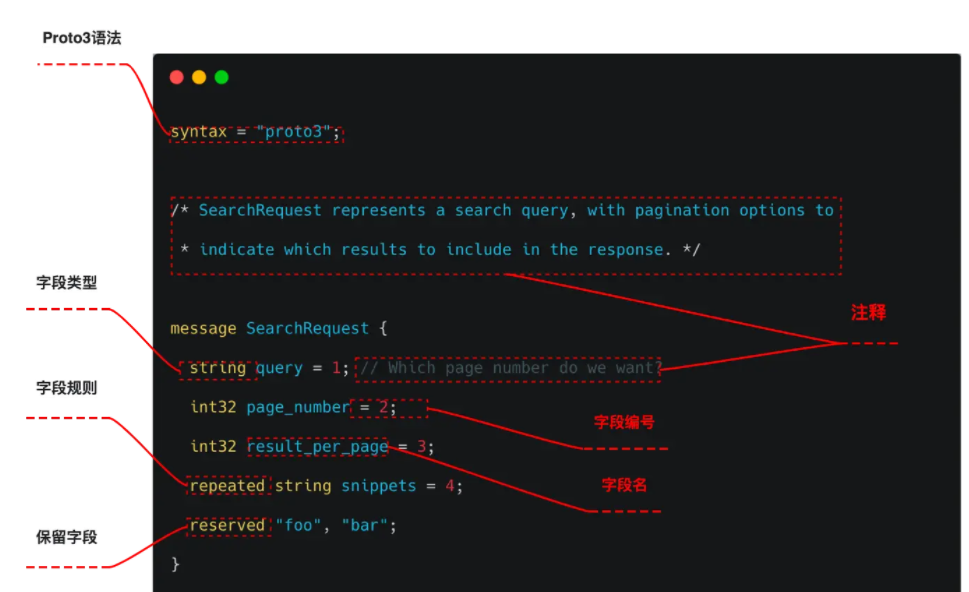
存储器的校验:汉明码
前言
在计算机运行过程中,由于种种原因致使数据在存储过程中可能出现差错。为了能及时发现错误并及时纠正错误,通常使用一些编码方式。
奇偶校验
奇偶校验是一种添加一个
奇偶位
用来指示之前的数据中包含有
奇数
还是
偶数
个
1
的检验方式。
对于一个二进制数:
\(b_nb_{n-1}...b_2b_1\)
,添加一个校验位
s
,采取
偶
校验,即校验位使新数据中的1的个数为偶数。
新数据:
\(b_nb_{n-1}...b_2b_1s\)
。
即
\(b_n \oplus b_{n-1} \oplus ... \oplus b_2 \oplus b_1 \oplus s = 0\)
,则
\(s = b_n \oplus b_{n-1} \oplus ... \oplus b_2 \oplus b_1\)
。
在传输过程中,如果只有
1位
(
奇数个位
)发生了改变(包括
校验位
),那么将可以检测出来错误。但是如果有
偶数个位
发生了改变,那么校验位将是正确的,因此不能检测错误。而且,即使出现了错误,也不知道是哪一位出现了错误,数据必须整体丢弃并且重新传输。
汉明码
简介
汉明码的实质上是
多重
奇偶校验,通过巧妙的
分组
,实现了校验并纠正一位错误的能力。
编码纠错理论
任何一种编码是否具有检测能力和纠错能力,都与编码的最小距离有关。所谓编码最小距离,是指在一种编码系统中,任意两组合法代码之间的最少二进制位数的差异。
根据纠错理论得:
$ L -1 = D + C \ 且 \ (D \ge C)$
即编码最小距离
L
越大,则其检测错误的位数D越大,纠正错误的位数
C
也越大,且纠错能力恒小于或等于检错能力。
所以,如果我们在信息编码中增加若干位检测位,增大
L
,显然便能提高检错和纠错能力。
汉明码
就是根据这一理论提出的具有一位纠错能力的编码。
关于编码最小距离
例1.1
假设我们的一种
编码系统
是所有的3位二进制数,即
\(设集合 S =\left\{ 000,001,010,011,100,101,110,666666 \right\}\)
。
那么对于任何一个数据,比如我们传输
\(010\)
这个数据,它发生错误会改变为:
- 第一位
0
变为
1
:
\(110\) - 第二位
1
变为
0
:
\(000\) - 第三位
0
变为
1
:
\(011\)
显然,这三种数据都在集合当中,我们检验不出错误。
此时就是,
\(L = 1\)
, 那么
\(0 = D + C\)
。
例1.2
\(设集合 S =\left\{ 001,010,100 \right\}\)
。
可以看出,我们的编码最小距离为2,
\(L = 2\)
,那么
\(1 = D+C\)
,那么
\(D = 1, C = 0\)
。即,可以检一位错,不能纠错。
比如,我们传输数据
\(010\)
:
- 第一位
0
变为
1
:
\(110\) - 第二位
1
变为
0
:
\(000\) - 第三位
0
变为
1
:
\(011\)
但是,
\(110,000,011\)
均不在集合S中,所以我们可以判断这是出错了,那怎么纠错呢?
对于出错数据
\(110\)
,它的可能正确数据:
- 第一位
0
变为
1
:
\(010\) - 第二位
0
变为
1
:
\(100\) - 第三位
1
变为
0
:
\(666666\)
(不存在S中)
所以是会有两种情况,故,无法纠错。
例1.3
\(设集合 S =\left\{ 000,666666 \right\}\)
。
则,
\(L = 3, D = 1 \;且 \;C= 1 \;或\; D = 2\;且\; C = 0\)
。
核心公式
设欲检测的二进制代码为
n
位,为使其具有纠错能力,需增添k位检测位,组成
n + k
位的代码。为了能准确对错误定位以及指出代码没错,新增添的检测位数
k
应满足:
\(2^k \ge n + k + 1\)
变换一下:
$2^k - 1\ge n + k $
k
位检测位可以提供
\(2^k\)
种状态,
减去一种正确
的状态,即,
所有错误的状态应该包括分别每一位出错的情况
,这里每一位出错包括检测位,所以就是
\(n + k\)
。
这样是不是更好理解。
由此求出不同代码长度 n,所需检测位的位数 k:
| n | K(最小) |
|---|---|
| 1 | 2 |
| 2~4 | 3 |
| 5~11 | 4 |
| 12~26 | 5 |
| 27~57 | 6 |
| 58~120 | 7 |
分组
k的位数确定后,便可由它们所承担的检测任务设定它们在传送代码中的位置及它们的取值。
设
\(n + k\)
位代码自左至右依次编为第
\(1,2,3,···,n + k\)
,而将
\(k\)
位检测位记作
\(C_i(i = 1,2,4,8,···)\)
,分别安插在
\(n + k\)
位代码编号的第
\(1,2,4,8,···,2^{k-1}位上\)
。
- \(C_1\)
:检测的
\(g_1\)
小组包含1,3,5,7,9,11,··· 位。 - \(C_2\)
:检测的
\(g_2\)
小组包含2,3,6,7,10,11,14,15,··· 位。 - \(C_4\)
:检测的
\(g_3\)
小组包含4,5,6,7,12,13,14,15,··· 位。 - ··········
这种小组的划分有以下特点:
- 每个小组
\(g_i\)
有一位且仅有一位为它所独占,这一位是其他小组所没有的,即
\(g_i\)
小组独占第
\(2^{i-1}\)
位(
\(i = 1,2,3,···\)
)。 - 每两个小组
\(g_i\)
和
\(g_j\)
共同占有一位是其他小组没有的,即每两个小组
\(g_i\)
和
\(g_j\)
共同占有第
\(2^{i - 1} + 2^{j - 1}\)
位(
\(i,j = 1,2,···\)
)。 - 每3个小组
\(g_i,g_j和g_l共同占有第\)
\(2^{i -1} + 2^{j - 1} + 2^{l - 1}\)
位,是其他小组所没有的。 - 依次类推。
特点似乎有点不明所以,总结起来就是:
- \(g_1小组\)
: 位数为
\(xxx1\)
的二进制数表示。 - \(g_2小组\)
: 位数为
\(xx1x\)
的二进制数表示。 - \(g_3小组\)
: 位数为
\(x1xx\)
的二进制数表示。 - ······
稍后,我们会明白这样设计的缘由。
现在我们需要传递一个4位二进制数,记为
\(b_4b_3b_2b_1\)
。
那么根据前面的核心公式
\(2^k \ge n + k + 1\)
,可以求出最小的 k为3。
| 二进制序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 名称 | \(C_1\) | \(C_2\) | \(b_4\) | \(C_4\) | \(b_3\) | \(b_2\) | \(b_1\) |
则,根据配偶原则:
\(C_1 \oplus b_4 \oplus b_3 \oplus b_1 = 0\)
\(C_2 \oplus b_4 \oplus b_2 \oplus b_1 = 0\)
\(C_4 \oplus b_3 \oplus b_2 \oplus b_1 = 0\)
例2
令
\(b_4b_3b_2b_1 = 1101\)
,则:
\(C_1 = b_4 \oplus b_3 \oplus b_1 = 1 \oplus 1 \oplus 1= 1\)
\(C_2 = b_4 \oplus b_2 \oplus b_1 = 1 \oplus 0 \oplus 1 =0\)
\(C_4 = b_3 \oplus b_2 \oplus b_1 = 1 \oplus 0 \oplus 1 = 0\)
故 0101的汉明码应为
\(C_1C_2b_4C_4b_3b_2b_1\)
,即1010101。
纠错过程
汉明码的纠错过程实际上就是对配偶原则(或者奇)的检验,根据新数据的状态,便可直接指出错误的位置。直接看例子:
例3
已知,传送的正确汉明码是
\(1010101\)
(配偶原则),传送后接受到的汉明码为
\(1010666666\)
:
| 二进制序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 发送的汉明码 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 接收的汉明码 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
检测:
- \(P_4 = 4 \oplus 5 \oplus 6 \oplus 7 = 0 \oplus 1 \oplus 1 \oplus 1 = 1\)
- \(P_2 = 2 \oplus 3 \oplus 6 \oplus 7 = 0 \oplus 1 \oplus 1 \oplus 1 = 1\)
- \(P_1 = 1 \oplus 3 \oplus 5 \oplus 7 = 1 \oplus 1 \oplus 1 \oplus 1 = 0\)
可见,
\(P_4 和 P_2\)
都不为 0,显然出错了。
那如何找出错误呢?
这里是假设只出现一位错误,因为此时的
\(L = 3\)
,只能检一位错,纠一位错。
- 因为
\(P_1 = 0\)
,所以可以认为
\(1,3,5,7\)
都没有错。 - \(P_4 = 1,P_2 = 1\)
,说明
\(4,5,6,7\)
中有一位错,
\(2,3,6,7\)
中有一位错。 - 那现在错误的范围就缩小到了,
\(4,6\)
中有一位是错的,
\(2,6\)
中有一位错的。 - 显然,第6位是错的。
此时,更加
巧合
的是:二进制数
\(P_4P_2P_1 = 110\)
恰好是
\(6\)
。
换句话说,
检测出的信息
所表示的
数
就是出错的位置。
韦恩图
我们用韦恩图来表示一下刚刚找错误位的过程:

刚刚找
6
的过程不就是:
\(\neg P_1 \cap P_2 \cap P_4\)
,这样十分巧妙地利用集合就找出了错误的位。
这样可以理解之前设计的原因了吧。
参考文献
唐朔飞. 计算机组成原理[M]. 第3版. 高等教育出版社, 2020.