前言
在上一篇
丝滑的贝塞尔曲线:从数学原理到应用
介绍贝塞尔曲线实现动画时给自己留了一个坑,实现的动画效果和CSS的
transition-timing-function: cubic-bezier
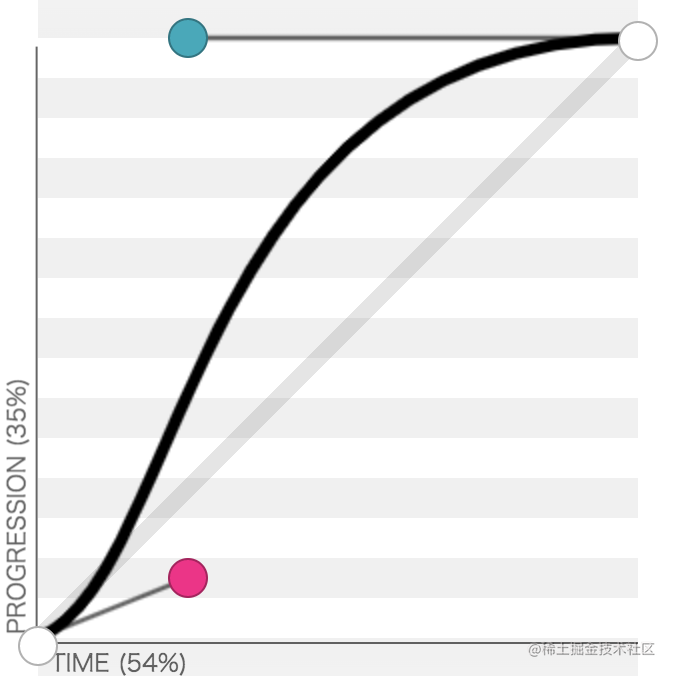
差别较大,如下图所示,红色为Linear、绿色为CSS的cubic-beizer、蓝色为自己实现的cbezier。本着有坑必填的原则,直接把Mozilla、Chromium的cubic-bezier实现源码给翻出来。

为什么和CSS效果不一致?假设贝塞尔曲线为
cubic-bezier(0.25, 0.1, 0.25, 1.0)
,X轴表示时间,Y轴表示元素样式属性变化量,设贝塞尔曲线为Q(t), 我直接把动画时间当做贝塞尔曲线的t,用Qy(X)来计算Y值。而正确的流程是
已知X值,根据Qx(t)=X对方程求根,其根即为t值,再根据t值求
Y = Qy(t)
。
整个流程的难点在于如何对Qx(t)=X求根t值,已知贝塞尔曲线方程为
Q(t) = X1 * (1 - t)³ + X2 * 3t(1 -t)² + X3 * 3t²(1 - t) + X4 * t³
由于曲线X轴范围为[0, 1],因此
X1=0
、
X4=1
, 从而Q(t)可写为
Q(t) = X2 * 3t(1 -t)² + X3 * 3t²(1 - t) + t³
将方程各项展开再合并成如下形式,主要是为了更方便的介绍浏览器源码实现。
Q(t) = ( ( (1.0 - 3.0 * X2 + 3.0 * X1) * t + (3.0 * X2 - 6.0 * X1) ) * t + (3.0 * X1) ) * t
浏览器是如何实现的
浏览器实现流程:使用参数
cubic-beizer(X1, Y1, X2, Y2)
生成贝塞尔曲线方程,根据传入的X值对方程求解得到t值,再将t传入Y方向的曲线方程计算Y值。难点在于如何求解方程的根,而求根一般可通过
Newton-Raphson method
牛顿法、
Bisection method
二分法。在深入浏览器源码之前,先介绍这两种求根方法,Mozilla和Chromium都基于这两种方法求解贝塞尔曲线的根。
Newton-Raphson method
牛顿法
牛顿法是求解数学方程的一种常用方法。它是一种迭代算法,通过不断逼近函数的根来寻找解。牛顿法可以用于求解实函数的根,也可以用于求解实函数的最小值或最大值。
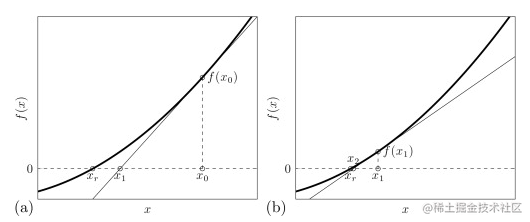
牛顿法的基本思想是:选择一个初始值
\(x_0\)
,然后通过递归计算出一个数列
\(x_1\)
,
\(x_2\)
, ...,
\(x_n\)
,使得每一项
\(x_{n+1}\)
都是函数
f(x)
在
\(x_n\)
处的切线与x轴的交点。也就是说,我们用当前的切线来近似替代原函数,从而得到更接近真实根的近似解。假设Xn处的函数值为
\(f(x_n)\)
、斜率为
\(f'(x_n)\)
,
\(X_{n+1}\)
为
\(f'(x_n)\)
与X轴的交点,从而有:
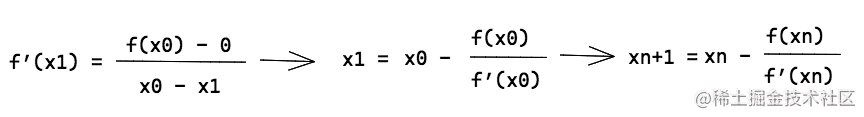
其中
f'(x)
是函数
f(x)
在 x 处的导数。每一次迭代中,我们通过计算
\(f(x_n)\)
和
\(f'(x_n)\)
来求出
\(x_{n+1}\)
的值,并将其作为下一次迭代的初始值。这个过程会不断重复,直到得到一个满足预定精度要求的解。
牛顿法的缺陷是,当斜率很小时,与X轴平行,得不到解。
Bisection method
二分法
Bisection method是一种求解方程的数值方法,可以用来找到一个函数f(x)=0的解。这种方法利用了连续函数的介值定理(Intermediate Value Theorem),即在一个区间[a,b]内,如果f(a)和f(b)的符号不同,那么必定存在至少一个数c属于[a,b],使得f(c)=0。
算法的基本思想是将一个区间[a,b]不断分成两半,然后找到包含根的那一半,并继续在该子区间内进行分割。每次分割之后,都会得到一个新的子区间,其长度是原来的一半。通过不断重复这个过程,可以越来越逼近根的位置。
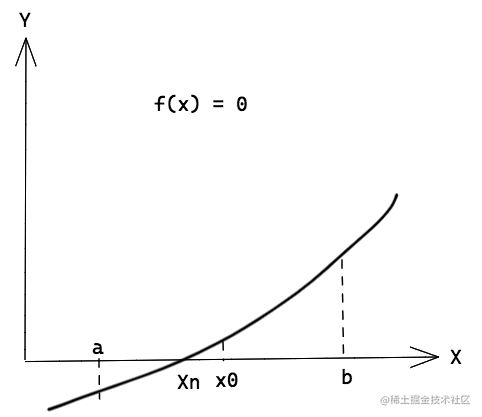
上图中f(x)递增,并且
f(a) < 0, f(b) > 0
。我们继续获取了a和b的中点x0。由上图可知
f(x0) > 0
,所以我们可以把x0看成是新的b。于是我们继续寻找a和x0的中点,重复上述过程,由于我们最大的误差就是区间的长度,所以当我们区间的长度缩减到足够小,那么就说明我们已经找到了一个足够近似的解。
Mozilla实现
由于
@greweb
已经将Mozilla的
缓动动画
通过JS实现,Mozilla的实现直接通过JS代码介绍。
主体结构和我们介绍的流程一致,定义bezier方法,参数分别为P1、P2坐标,返回结果为函数
BezierEasing
, 其内部会根据传入的X值,调用getTForX(x)求根得到t,最后调用
calcBezier(t, mY1, mY2)
计算Y轴的曲线值。
export function bezier (mX1, mY1, mX2, mY2) {
// ...其他逻辑
return function BezierEasing (x) {
// Because JavaScript number are imprecise, we should guarantee the extremes are right.
if (x === 0 || x === 1) {
return x;
}
return calcBezier(getTForX(x), mY1, mY2);
};
};
calcBezier
函数比较简单,就是根据贝塞尔曲线方程以及传入的t值计算结果,由于要计算一阶导数,将Q(t)拆成了三部分,
1.0 - 3.0 * X2 + 3.0 * X1
对应A函数,
3.0 * X2 - 6.0 * X1
对应B函数,
3.0 * X1
对应C函数。
// Q(t) = ( ( (1.0 - 3.0 * X2 + 3.0 * X1) * t + (3.0 * X2 - 6.0 * X1) ) * t + (3.0 * X1) ) * t
function A (aA1, aA2) { return 1.0 - 3.0 * aA2 + 3.0 * aA1; }
function B (aA1, aA2) { return 3.0 * aA2 - 6.0 * aA1; }
function C (aA1) { return 3.0 * aA1; }
// at为t,aA1表示x1或者x2,aA2表示y1或者y2
// 其形式和p0 * Math.pow(1 - t, 3) + p1 * 3 * t * Math.pow(1 - t, 2) + p2 * 3 * Math.pow(t, 2) * (1 - t) + p3 * Math.pow(t, 3)一致
function calcBezier (aT, aA1, aA2) { return ((A(aA1, aA2) * aT + B(aA1, aA2)) * aT + C(aA1)) * aT; }
难点在于
getTForX
函数,其作用是根据X值计算t,涉及到曲线方程求根,而求根一般可通过
Newton-Raphson method
牛顿法、
Bisection method
二分法, 也就是我上面介绍的两种方法。
而Mozilla在求根时会根据斜率选择不同的方法,为了提升计算性能,在求根之前先采样,使用sampleValues缓存X轴方向当t=0,0.1,...,0.9, 1时对应的曲线值。
// kSplineTableSize为11,kSampleStepSize为1.0 / (11 - 1.0) = 0.1;
// sampleValues存储样本值的目的是提升性能,不用每次都计算。
var sampleValues = float32ArraySupported ? new Float32Array(kSplineTableSize) : new Array(kSplineTableSize);
// i从0到10,sampleValues长度为11
for (var i = 0; i < kSplineTableSize; ++i) {
// i * kSampleStepSize的范围0到1(10 * 0.1);
// sampleValues[0] = calcBezier(0, mX1, mX2);
// sampleValues[1] = calcBezier(0.1, mX1, mX2);
// ...
// sampleValues[9] = calcBezier(0.9, mX1, mX2);
// sampleValues[10] = calcBezier(1, mX1, mX2);
sampleValues[i] = calcBezier(i * kSampleStepSize, mX1, mX2);
}
对于
getTForX
函数的实现,首先遍历
sampleValues
数组,找到小于目标值aX的最大值,为了减少求根的遍历次数,为了使guessForT尽量接近目标根,使用
(aX - sampleValues[currentSample]) / (sampleValues[currentSample + 1] - sampleValues[currentSample])
计算出差值在两个样本区间的百分比dist,那么
intervalStart + dist * KSampleStepSize
即为根据样本值能找到最接近目标根
guessForT
的初始值。
// 已知X值,根据X值求解T值
var NEWTON_MIN_SLOPE = 0.001;
function getTForX (aX) {
var intervalStart = 0.0;
var currentSample = 1;
// lastSample为10
var lastSample = kSplineTableSize - 1;
// sampleValues[i]表示i从0以0.1为step,每一步对应的曲线的X坐标值,直到X坐标值小于等于aX
// 假如aX=0.4,则sampleValues[currentSample]<=aX为止
for (; currentSample !== lastSample && sampleValues[currentSample] <= aX; ++currentSample) {
// intervalStart为到aX经过的step步骤
intervalStart += kSampleStepSize; // kSampleStepSize为0.1
}
//TODO:currentSample为什么要减1?sampleValues[currentSample]大于了ax,所以要--,使得sampleValues[currentSample]<=ax
--currentSample;
// Interpolate to provide an initial guess for t
// ax-sampleValues[currentSample]为两者之间的差值,而(sampleValues[currentSample + 1] - sampleValues[currentSample])一个步骤之间的总差值。
var dist = (aX - sampleValues[currentSample]) / (sampleValues[currentSample + 1] - sampleValues[currentSample]);
// guessForT为预计的初始T值,很粗糙的一个值,接下来会基于该值求根(t值)。
var guessForT = intervalStart + dist * kSampleStepSize;
// 预测的T值对应位置的斜率
var initialSlope = getSlope(guessForT, mX1, mX2);
// 当斜率大于0.05729°时,使用newtonRaphsonIterate算法预测T值。0.05729是一个很小的斜率
if (initialSlope >= NEWTON_MIN_SLOPE) {
return newtonRaphsonIterate(aX, guessForT, mX1, mX2);
} else if (initialSlope === 0.0) { // 当斜率为0,则直接返回
return guessForT;
} else { // 当斜率小于0.05729并且不等于0时,使用binarySubdivide
// 求得的根t,位于intervalStart和intervalStart + kSampleStepSize之间, mX1、mX2分别对应p1、p2的X坐标
return binarySubdivide(aX, intervalStart, intervalStart + kSampleStepSize, mX1, mX2);
}
}
使用
getSlope
函数计算guessForT的斜率initialSlope,
NEWTON_MIN_SLOPE
为测试的一个斜率临界(0.001),当大于等于该斜率时使用牛顿法球根,否则使用二分法球根。牛顿法实现:
var NEWTON_ITERATIONS = 4;
function newtonRaphsonIterate (aX, aGuessT, mX1, mX2) {
// NEWTON_ITERATIONS为4, 只进行了4次迭代, 根据精度和性能之间做了平衡。
for (var i = 0; i < NEWTON_ITERATIONS; ++i) {
// 计算t值对应位置的斜率
var currentSlope = getSlope(aGuessT, mX1, mX2);
if (currentSlope === 0.0) {
return aGuessT;
}
// 假设f(t) = 0,求解方程的根。其f(t)=calcBezier(t) - ax
// 牛顿-拉佛森方法: Xn-1 = Xn - f(t) / f'(t),应用到求贝塞尔曲线的根:Tn = Tn+1 - (calcBezier(t) - ax) / getSlope(t)
var currentX = calcBezier(aGuessT, mX1, mX2) - aX;
aGuessT -= currentX / currentSlope;
}
// 这里只迭代了4次,求得近似值
return aGuessT;
}
牛顿法求根会不断根据上一个值
\(x_n\)
迭代下一个值
\(x_{n+1}\)
,而
newtonRaphsonIterate
函数仅仅迭代了4次,是根据精度和性能之间的平衡考量。根据牛顿法公式:
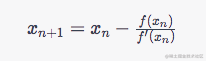
这里的f(t) = calcBezier(t) - aX, f'(t)即计算在t位置的斜率用
getSlope(aGuessT, mX1, mX2)
表示,所以aGuessT的迭代值可写为
aGuessT = aGuessT - f(t)/f'(t)
。当斜率为0时,aGuessT即为最终值;否则直到迭代4次结束。
当斜率小于
NEWTON_MIN_SLOPE
时,降级使用
Bisection method二分法
,要计算的t值肯定在[intervalStart、intervalStart + kSampleStepSize]之间,并且f(intervalStart)和f(intervalStart + kSampleStepSize)的乘积小于0,满足二分法条件。
binarySubdivide(aX, intervalStart, intervalStart + kSampleStepSize, mX1, mX2);
二分法会不断缩小[a,b]范围,直到计算的值和目标值aX差值小于
SUBDIVISION_PRECISION
,也即小于0.0000001。 或者大于最大迭代次数
SUBDIVISION_MAX_ITERATIONS
也会终止。
var SUBDIVISION_PRECISION = 0.0000001;
var SUBDIVISION_MAX_ITERATIONS = 10;
// 二分球根法:
// 求得的根t,位于aA和aB之间, mX1、mX2分别对应p1、p2的X坐标
// https://zhuanlan.zhihu.com/p/112845185
function binarySubdivide (aX, aA, aB, mX1, mX2) {
var currentX, currentT, i = 0;
do {
currentT = aA + (aB - aA) / 2.0;
// 假设f(t) = 0,求解方程的根。其f(t)=calcBezier(t) - ax
currentX = calcBezier(currentT, mX1, mX2) - aX;
if (currentX > 0.0) {
aB = currentT;
} else {
aA = currentT;
}
// 如果currentX小于等于最小精度(SUBDIVISION_PRECISION)或者超过迭代次数SUBDIVISION_MAX_ITERATIONS,则终止
} while (Math.abs(currentX) > SUBDIVISION_PRECISION && ++i < SUBDIVISION_MAX_ITERATIONS);
return currentT;
}
aA、aB为初始范围,每次迭代计算中点
currentT = aA + (aB - aA) / 2.0
, 然后使用其值计算currentX(
calcBezier(currentT, mX1, mX2)
)。当currentX大于aX时,说明currentT还大于目标t,则将aB赋值为currentT缩小右边界;否则将aA赋值为currentT缩小左边界。
至此,Mozilla的实现介绍完毕。
Chromium实现
实现和Mozilla类似,核心部分
SolveCurveX
也是对已知的X和曲线方程求解t。先迭代样本数组,找到第一个大于等于X的样本值,设置最接近的值为t2, 在区间[t0, t1]中。
在选择牛顿法和二分法时,Chromium和Mozilla有些区别,Chromium先使用牛顿法迭代
kMaxNewtonIterations
4次直到计算值小于精度
newton_epsilon
,或者一阶导(斜率)
SampleCurveDerivativeX(t2)
小于最小斜率
kBezierEpsilon
也会中止。
如果牛顿法未计算出满足精度要求的根,则继续使用二分法判断。和Mozilla的区别在于没限制迭代次数,一直根据
t0<t1
条件迭代,直到找到满足精度的t2。r
double CubicBezier::SolveCurveX(double x, double epsilon) const {
double t0;
double t1;
double t2 = x;
double x2;
double d2;
int i;
// Linear interpolation of spline curve for initial guess.
// 迭代样本值,找到和x最接近的初始t,这里为t2,在t0和t1之间。
double delta_t = 1.0 / (CUBIC_BEZIER_SPLINE_SAMPLES - 1);
for (i = 1; i < CUBIC_BEZIER_SPLINE_SAMPLES; i++) {
if (x <= spline_samples_[i]) {
t1 = delta_t * i;
t0 = t1 - delta_t;
// 根据x差值在所在区间的百分占比计算t在阶段间的百分占比,t2为接近x根的初始值
t2 = t0 + (t1 - t0) * (x - spline_samples_[i - 1]) /
(spline_samples_[i] - spline_samples_[i - 1]);
break;
}
}
// Perform a few iterations of Newton's method -- normally very fast.
// See https://en.wikipedia.org/wiki/Newton%27s_method.
// 牛顿法的精度
double newton_epsilon = std::min(kBezierEpsilon, epsilon);
for (i = 0; i < kMaxNewtonIterations; i++) {
// x2为t2所在x值和目标x差值
x2 = SampleCurveX(t2) - x;
// 如果差值小于精度则任务t2即为方程根
if (fabs(x2) < newton_epsilon)
return t2;
// d2为t2位置的斜率
d2 = SampleCurveDerivativeX(t2);
// 如果斜率小于最小精度kBezierEpsilon,任务与x轴平行,无法继续计算
if (fabs(d2) < kBezierEpsilon)
break;
// 否则使用牛顿法继续迭代
t2 = t2 - x2 / d2;
}
if (fabs(x2) < epsilon)
return t2;
// Fall back to the bisection method for reliability.
// 降级使用二分法
while (t0 < t1) {
x2 = SampleCurveX(t2);
// 如果x2小于最小精度,则任务为要求的根
if (fabs(x2 - x) < epsilon)
return t2;
// 下面的流程和二分法流程一致
if (x > x2)
t0 = t2;
else
t1 = t2;
t2 = (t1 + t0) * .5;
}
// Failure.
return t2;
}
效果对比
使用封装的动画函数
animate
执行动画,查看动画效果。easing为
bezier-easing(0.25, 0.1, 0.25, 1.0)
,和CSS指定贝塞尔曲线一致。
animate(bezieRef2.current, {
duration: 2000,
easing: 'bezier-easing(0.25, 0.1, 0.25, 1.0)',
styles: [{ left: !ended ? '0%' : '100%' }, { left: !ended ? '100%' : '0%' } ]
})
animate函数内部调用
resolveEasing
解析传入的字符串
bezier-easing(0.25, 0.1, 0.25, 1.0)
,并生成贝塞尔曲线函数,生成的曲线函数形式为
function BezierEasing (x): number
,根据传入的X(时间百分比)求解t值,再根据t计算Y值(元素位置)。
/**
* 元素动画
* @param el DOM元素
* @param props 动画属性
*/
function animate(el, props) {
const duration = props.duration;
const easingFunc = resolveEasing(props.easing);
const styleFuncs = resolveStyles(el, props.styles);
const start = Date.now();
const animationHandle = () => {
const timeRatio = (Date.now() - start) / duration;
if (timeRatio <= 1) {
const percent = easingFunc(timeRatio);
for (const key in styleFuncs) {
const elementStyle = el.style;
elementStyle[key] = styleFuncs[key](percent);
}
requestAnimationFrame(animationHandle);
}
};
animationHandle();
}
原始的CSS实现缓动动画,非常简单,直接设置样式即可:
.fade-in-cbezier {
transition: all 2s;
transition-timing-function: cubic-bezier(0.25, 0.1, 0.25, 1.0);
}
设置相同的曲线参数,自己实现的贝塞尔缓动动画和CSS对比,其效果几乎完全一致,图中
绿色
的为CSS,
黄色
为自己实现的动画效果。

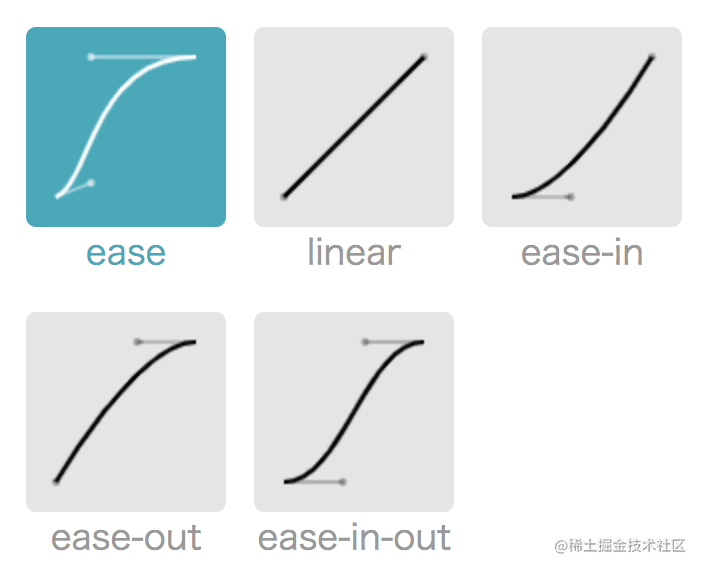
CSS 默认提供了几个固定的贝塞尔曲线
linear
、
ease-in
、
ease-out
、
ease-in-out
。
- linear 匀速移动,cubic-bezier(0.0, 0.0, 1.0, 1.0)
- ease-in 先慢后快 cubic-bezier(0.42, 0, 1.0, 1.0)
- ease-out 先快后慢 cubic-bezier(0, 0, 0.58, 1.0)
- ease-in-out 慢速、提速、减速三个阶段 cubic-bezier(0.42, 0, 0.58, 1.0)
可通过
在线预览
查看动贝塞尔曲线。
运行效果:
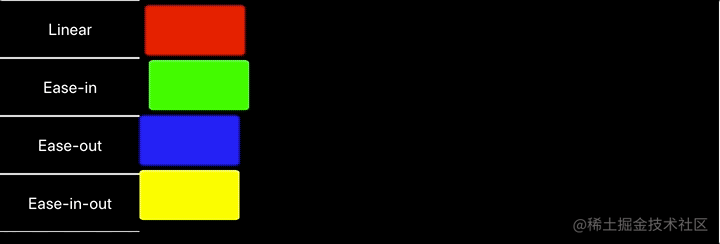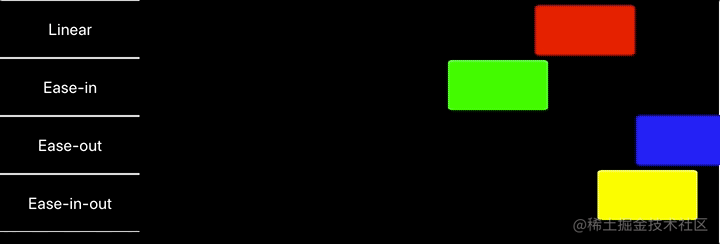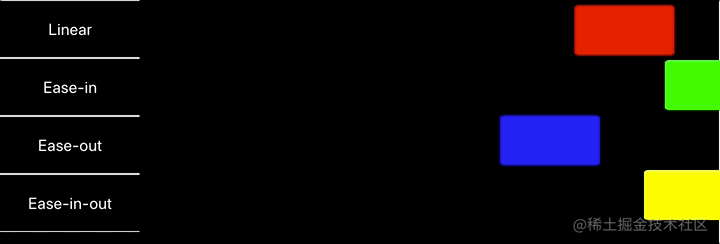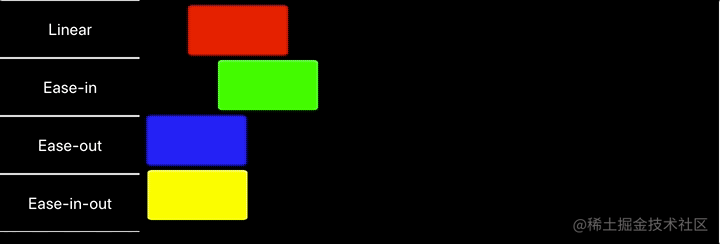
动画库入门
标星44.8k的
animejs
,其核心部分也使用了Mozilla的贝塞尔曲线动画,另外一个重要的问题是如何转换单位,如将left设置为
50%
、
20em
或者
50vw
,只有将单位统一才能计算中间差值。
animejs将元素的初始值使用
convertPxToUnit
函数转换为目标单位,以
convertPxToUnit(el, '50', 'em') )
为例,
convertPxToUnit
为元素el的父元素附加一个临时子要素
tempEl
,目标单位为
em
,设置
tempEl
的宽度为
100em
,然后得到因子
factor=100em/offestWidth
,即
目标长度/像素
,那么转换后的值为
factor * parseFloat ('50')
。
/**
* 将像素值转换为目标单位值
* @param {*} el
* @param {*} value
* @param {*} unit
* @returns
*/
function convertPxToUnit(el: Element, value: string, unit: string) {
const baseline = 100;
// 创建一个和el类型一样的要素
const tempEl = document.createElement(el.tagName);
// 获取要素的parent
const parentEl = (el.parentNode && (el.parentNode !== document)) ? el.parentNode : document.body;
parentEl.appendChild(tempEl);
tempEl.style.position = 'absolute';
// 设置基线为100个目标单位
tempEl.style.width = baseline + unit;
// 宽度因子,目标长度/一个像素
const factor = baseline / tempEl.offsetWidth;
parentEl.removeChild(tempEl);
// parseFloat会将最后的单位忽略得到数值
const convertedUnit = factor * parseFloat(value);
return convertedUnit;
}
在执行动画时,可同时设置多个属性,如opacity、height、width、left、top等,
resolveStyles
函数遍历每个属性并为其生成一个获取中间值的函数,如设置
{width: '30%'}
, 那么目标值destValue为30。如何获取width的当前值并转换单位为
%
?先调用
getComputedStyle(el).getPropertyValue(key.toLowerCase())
获取其像素值,再通过前面实现的
convertPxToUnit
将像素值转换为
%
。有了startValue和destValue,中间值即可通过
startValue + total * percent
计算。
export type StyleProperties = {
[x: string]: string | number;
}
function resolveStyles(el: Element, styles: StyleProperties) {
const keys = Object.keys(styles);
const styleFuncs: { [x: string]: (t: number) => number | string } = {};
for (const key of keys) {
const value = styles[key] + '';
const unit = <string>getUnit(value);
const destValue = parseFloat(value);
const styleValue = getComputedStyle(el).getPropertyValue(key.toLowerCase());
const startValue = unit ? convertPxToUnit(el, styleValue, unit) : parseFloat(styleValue);
const total = destValue - startValue;
styleFuncs[key] = (percent: number) => {
const curVal = startValue + total * percent;
return unit ? curVal + unit : curVal;
}
}
return styleFuncs;
}
对外提供的API格式为
animate(el: HTMLElement, props: AnimationProps)
,props包括duration、styles、easing三个参数,函数会根据
(Date.now() - start) / duration
计算动画执行进度,然后遍历styleFuncs设置每个样式属性的中间值。
export type AnimationProps = {
duration: number;
styles: StyleProperties;
easing: string;
}
/**
* 元素动画
* @param el DOM元素
* @param props 动画属性
*/
export function animate(el: HTMLElement, props: AnimationProps): { pause: () => void } {
const duration = props.duration;
const easingFunc = resolveEasing(props.easing);
const styleFuncs = resolveStyles(el, props.styles);
const cAniInstance = {
paused: false,
}
const start = Date.now();
const animationHandle = () => {
if (cAniInstance.paused) {
return;
}
const timeRatio = (Date.now() - start) / duration;
if (timeRatio <= 1) {
const percent = easingFunc(timeRatio);
for (const key in styleFuncs) {
const elementStyle = el.style as any;
elementStyle[key] = styleFuncs[key](percent);
}
requestAnimationFrame(animationHandle);
}
}
requestAnimationFrame(animationHandle);
return {
pause: () => {
cAniInstance.paused = true;
}
}
}
使用比较简单,实现一个弹窗效果:
animate(ref1.current, {
duration: 500,
easing: 'cbezier(0.25, 0.1, 0.25, 1.0)',
styles: {
opacity: '1',
width: '300px',
height: '200px',
left: '30%',
top: '30%',
}
})

实现鼠标跟踪,由于gif图像有丢帧,效果不是很明显,Demo已上传到
cbezier
。
const mouseMove = throttle((e) => {
const x = e.offsetX, y = e.offsetY;
if (aniPlay) {
aniPlay.pause();
}
// console.log(ref1.current.style.left, ref1.current.style.top);
aniPlay = animate(ref1.current, {
duration: 15,
// easing: 'ease-out',
easing: 'cbezier(0.25, 0.1, 0.25, 1.0)',
styles: {
left: x + 'px',
top: y + 'px',
}
})
}, 15);
parentRef.current.addEventListener('mousemove', mouseMove);

下一步计划: 实现完整的动画库
hiani.js
。以上仅仅是一个入门版动画,要实现和animejs一样的效果,还需要支持
rotate
、
scale
、
translate
、
skew
等transform样式以及颜色变化,下一步将完善动画库支持更多样式属性、提供play、pause、reset等完整的函数控制动画。
参考
1、
Bezier Curve as Easing Function
2、
Bezier Curve based easing functions – from concept to implementation
3、
mozilla贝塞尔实现
4、
Chromium贝塞尔实现
5、
Newton Raphson method
6、
Newton Raphson formula
7、
牛顿法和二分法的区别
8、
二分法介绍
**写在最后,如果大家有疑问可直接留言,一起探讨!感兴趣的可以点一波关注, 文章也在
掘金
上同步。