「学习笔记」双连通分量、割点与桥
文章图片全部来自 Oi-wiki,部分图片加以修改
前面我们在学 tarjan 算法时,提到过强连通分量,即有向图上的环,那么无向图上是否也有强连通分量呢?很遗憾,没有
但是,无向图有双连通分量!分为点双连通和边双连通(下面简称点双和边双)。
边双连通分量
概念
在一张联通的无向图中,对于两个点
\(x\)
和
\(y\)
,删去图上的任意一条边,两个点始终保持联通,则这两个点是边双连通。
边双连通分量,即
极大边双连通子图
,边双连通分量中的任意两点都是边双连通的,且如果加入一个不属于该子图的点,都会导致这个图不再满足两两之间边双的性质。
在无向图中。删掉一条边,导致两个图不连通了,这条边就是
割边
,也叫做
桥
。
边双连通具有传递性,即如果
\(x\)
与
\(y\)
边双连通,
\(y\)
与
\(z\)
边双连通,则
\(x\)
与
\(z\)
也边双连通。
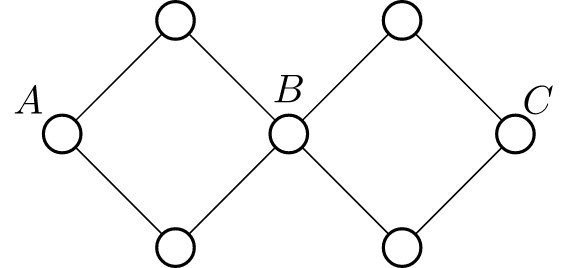
如图,在这张图中,
\(A\)
与
\(B\)
边双连通,
\(B\)
与
\(C\)
边双连通,根据传递性,
\(A\)
与
\(C\)
边双连通。(即使不跟据传递性,他们也的确是边双连通)
找桥的过程
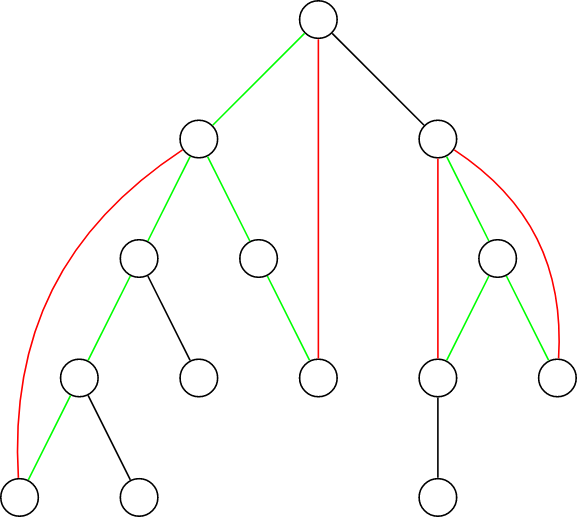
如图,绿色的边和黑色的边都是树边,红色的边是返祖边。
我们发现,每一条返祖边都对应着一条树上的简单路径,即覆盖了树上的一些边,覆盖了的边我们用绿边表示,黑色的边没有被覆盖。我们如果删去返祖边或者任意一条绿边,都不会影响图的连通性(如果删掉返祖边就从绿边走,如果删掉绿边就从返祖边走),但是,如果我们删掉黑边,那么整个图就会被一分为二,不再保持联通,
这些黑色的边就是桥
,同时
返祖边和绿边一定不是桥
。
这样,我们只要找到所有的桥,就能确定边双连通分量了。
找边双连通分量,我们可以用 tarjan 算法。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim; // 打上时间戳
for (int i = h[u], v; i; i = e[i].nxt) {
v = e[i].v;
if ((i ^ 1) == fa) continue;
if (!dfn[v]) { // 如果这个点从未被搜过
tarjan(v, i); // 继续往下搜
low[u] = min(low[u], low[v]); // 正常更新 low 值
if (low[v] > dfn[u]) { // 如果 v 点无法通过返祖边向上返回到 u 点即往上
e[i].ok = e[i ^ 1].ok = 1; // 那么这条边就是桥
}
// 不理解的话可以想一想,v 点不管怎么向上都不能到达 u 点即更靠上的位置,那 u -> v 这条边就没有被返祖边覆盖,它就是桥
}
else { // 如果这个点已经被搜过了(说明这条边是返祖边)
low[u] = min(low[u], dfn[v]); // 更新 low 值(比较的是 dfn[v],不是 low[v])
}
}
}
找边双连通分量
有两种方式,像找强连通分量那样用一个栈,或者标记桥之后再 dfs。
洛谷模板题测试,用栈比标记桥更快一些。
- 用栈找双连通分量
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
sta.push_back(u);
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
ans[++ dcc].push_back(u);
while (sta.back() != u) {
ans[dcc].push_back(sta.back());
sta.pop_back();
}
sta.pop_back();
}
}
- 标记桥,dfs。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
ok[i] = 1;
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
}
void dfs(int u) { // dfn 要清零,你也可以再开一个数组
ans[dcc].push_back(u);
dfn[u] = 1;
for (auto [v, i] : son[u]) {
if (dfn[v] || ok[i]) continue;
dfs(v);
}
}
点双连通分量
概念
在一张联通的无向图中,对于两个点
\(x\)
和
\(y\)
,删去图上的任意一个点(不能删去
\(x\)
和
\(y\)
),两个点始终保持联通,则这两个点是点双连通。
删去一个点,会删掉这个点以及这个点所连接的所有的边,所以桥连接的两个点都是割点。
点双连通分量,即
极大点双连通子图
,点双连通分量中的任意两点都是点双连通的,且如果加入一个不属于该子图的点,都会导致这个图不再满足两两之间点双的性质。
在无向图中。删掉一个点,导致两个图不连通了,这个点就是
割点
。
点双连通没有传递性,即如果
\(x\)
和
\(y\)
点双联通,
\(y\)
和
\(z\)
点双联通,
\(x\)
和
\(z\)
不一定点双联通。
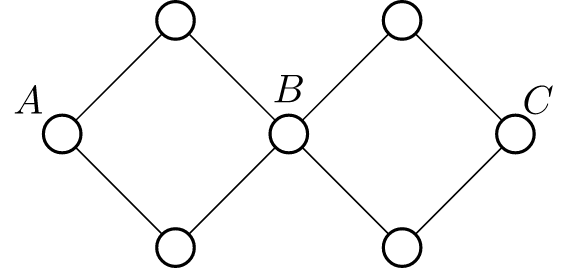
举个例子。
\(A\)
与
\(B\)
点双连通,
\(B\)
与
\(C\)
点双连通,但是
\(A\)
与
\(C\)
并不是点双连通。(割点为
\(B\)
)
过程
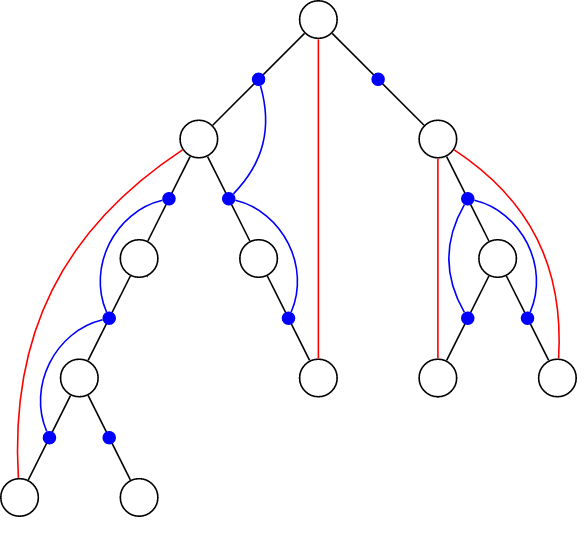
如图,黑色的边是树边,红色的边是返祖边,每一条返祖边对应着一条简单路径。
现在,我们将每一条边看作是一个点,即图上蓝色的点,返祖边所覆盖的简单路径上的边都连上边,即图上的蓝边。
这样,要判断点是否为割点,只要判断这个点连出去的边是否在一个连通分量里,都在一个连通分量里,就不是割点,否则就是割点
这里还有另一种做法。
对于某个顶点
\(u\)
,如果存在至少一个顶点
\(v\)
,使得
low[v]
\(\geq\)
dfn[u]
,即不能回到祖先,那么
\(u\)
点为割点。
但这个做法唯独不适用于搜索树的起始点,即搜索树的根,如果根只有一个子树,那我们把根节点删去,对图的连通性不会有任何影响,即根节点不是割点,如果根节点有着至少两个子树,那么根节点就是割点。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ cnt;
int son = 0;
for (int i = h[u], v; i; i = e[i].nxt) {
v = e[i].v;
if (v == fa) continue;
if (!dfn[v]) {
++ son;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
ok[u] = 1;
++ dcc;
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (fa == 0 && son < 2) ok[u] = 0;
}
应用
在题目中,桥一般出现在“给定一张无向图,问是否有一种方案,能给定向,同时保证每个点都能走到”这样类似的题目上,在这道题中,有桥就没有可行方案,倘若要输出方案,我们可以利用 dfs 生成树。
由于边双比点双有着更好的性质,所以一般题目都是有关边双的。
关于用
vector
来写 tarjan
优点:动态空间,方便。
缺点:
慢!
上面的代码我们也看到了,有些题目有重边,用一般的
vector
存图方式判断是否走过重边,这里有一个方式可以实现用
vector
来找重边,那就是将
vector
的变量类型改成
pair
,第一个元素存到达的节点,第二个元素存这条边的编号,如果不保险可以再开一个
vector
、结构体或两个数组来存第
\(i\)
条边的两个端点的编号,像这样。
e.push_back({0, 0});
for (int i = 1, x, y; i <= m; ++ i) {
scanf("%d%d", &x, &y);
son[x].push_back({y, i});
son[y].push_back({x, i});
e.push_back({x, y});
}
这样,我们在 tarjan 判重边的的过程中可以直接判断编号了。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[v], low[u]);
if (low[v] > dfn[u]) {
ok[i] = 1;
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
}
对于找割点,我们直接用
vector
就行了,这里不存在任何限制,就是会慢。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ cnt;
st[++ top] = u;
int ch = 0;
for (int v : son[u]) {
if (v == fa) continue;
if (!dfn[v]) {
++ ch;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
ok[u] = 1;
++ dcc;
while (st[top + 1] != v) {
ans[dcc].push_back(st[top --]);
}
ans[dcc].push_back(u);
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (fa == 0 && ch == 0) ans[++ dcc].push_back(u);
if (fa == 0 && ch < 2) ok[u] = 0;
}
题目
都是来源于洛谷的模板题
P8436 【模板】边双连通分量
- 直接用栈来找边双。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 5e5 + 5;
const int M = 2e6 + 5;
int n, m, cnt = 1, tim, top, dcc;
int h[N], dfn[N], low[N];
bool ok[M];
vector<pii> son[N];
vector<int> ans[N], sta;
struct edge {
int v, nxt;
bool ok;
} e[M << 1];
void add(int u, int v) {
e[++ cnt].nxt = h[u];
e[h[u] = cnt].v = v;
}
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
sta.push_back(u);
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
ans[++ dcc].push_back(u);
while (sta.back() != u) {
ans[dcc].push_back(sta.back());
sta.pop_back();
}
sta.pop_back();
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1, x, y; i <= m; ++ i) {
scanf("%d%d", &x, &y);
son[x].push_back({y, i});
son[y].push_back({x, i});
}
for (int i = 1; i <= n; ++ i) {
if (!dfn[i]) {
tarjan(i, 0);
}
}
printf("%d\n", dcc);
for (int i = 1; i <= dcc; ++ i) {
int siz = ans[i].size();
printf("%d ", siz);
for (int j : ans[i]) {
printf("%d ", j);
}
putchar('\n');
}
return 0;
}
- 标记桥,通过 dfs 来找边双。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 5e5 + 5;
const int M = 2e6 + 5;
int n, m, cnt = 1, tim, top, dcc;
int h[N], dfn[N], low[N];
bool ok[M];
vector<int> ans[N];
vector<pii> son[N];
struct edge {
int v, nxt;
bool ok;
} e[M << 1];
void add(int u, int v) {
e[++ cnt].nxt = h[u];
e[h[u] = cnt].v = v;
}
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
ok[i] = 1;
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
}
void dfs(int u) {
ans[dcc].push_back(u);
dfn[u] = 1;
for (auto [v, i] : son[u]) {
if (dfn[v] || ok[i]) continue;
dfs(v);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1, x, y; i <= m; ++ i) {
scanf("%d%d", &x, &y);
son[x].push_back({y, i});
son[y].push_back({x, i});
}
for (int i = 1; i <= n; ++ i) {
if (!dfn[i]) {
tarjan(i, 0);
}
}
memset(dfn, 0, sizeof dfn);
for (int i = 1; i <= n; ++ i) {
if (!dfn[i]) {
++ dcc;
dfs(i);
}
}
printf("%d\n", dcc);
for (int i = 1; i <= dcc; ++ i) {
int siz = ans[i].size();
printf("%d ", siz);
for (int j : ans[i]) {
printf("%d ", j);
}
putchar('\n');
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5 + 5;
const int M = 2e6 + 5;
int n, m, cnt, top, dcc;
int h[N], dfn[N], low[N], st[N];
bool ok[N];
vector<int> son[N], ans[N];
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ cnt;
st[++ top] = u;
int ch = 0;
for (int v : son[u]) {
if (v == fa) continue;
if (!dfn[v]) {
++ ch;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
ok[u] = 1;
++ dcc;
while (st[top + 1] != v) {
ans[dcc].push_back(st[top --]);
}
ans[dcc].push_back(u);
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (fa == 0 && ch == 0) ans[++ dcc].push_back(u);
if (fa == 0 && ch < 2) ok[u] = 0;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1, x, y; i <= m; ++ i) {
scanf("%d%d", &x, &y);
son[x].push_back(y);
son[y].push_back(x);
}
cnt = 0;
for (int i = 1; i <= n; ++ i) {
if (!dfn[i]) {
top = 0;
tarjan(i, 0);
}
}
printf("%d\n", dcc);
for (int i = 1; i <= dcc; ++ i) {
printf("%d ", (int)ans[i].size());
for (int j : ans[i]) {
printf("%d ", j);
}
putchar('\n');
}
return 0;
}