写在前面
深知新手在接触毫米波雷达板硬件时需要花费的沉没成本,因此在行将告别毫米波雷达之际,总结这两年以来在毫米波雷达上的一些经验和教训。
本文档用于为实现基于
AWR1243BOOST
等单板毫米波雷达开发提供参考指南与解决方案,主要包括
硬件配置
、
基础参数
、
信号模型
、
应用DEMO开发
以及
可深入研究方向思考
等;为更好地匹配后续级联雷达应用的学习路线,在本手册中会尽可能同化单板雷达和级联雷达中的相关表述。
本指南作者信息:
Xuliang
,联系方式:
xxxxxxxxx@xxx.edu.cn
。未经本人允许,请勿用于商业和学术用途。
希望后者在使用本指南时可以考虑引用作者在毫米波雷达旅途中的相关工作,如本文参考文献[1].
本章节为信号模型章节,主要解读
时域信号模型
、
空域信号模型
和
信号处理栈
。
往期内容:
眼观四海:自动驾驶&4D成像毫米波雷达 如今几何?
扬帆起航:毫米波雷达开发手册之硬件配置
初出茅庐:毫米波雷达开发手册之基础参数
信号模型分析
时域信号模型
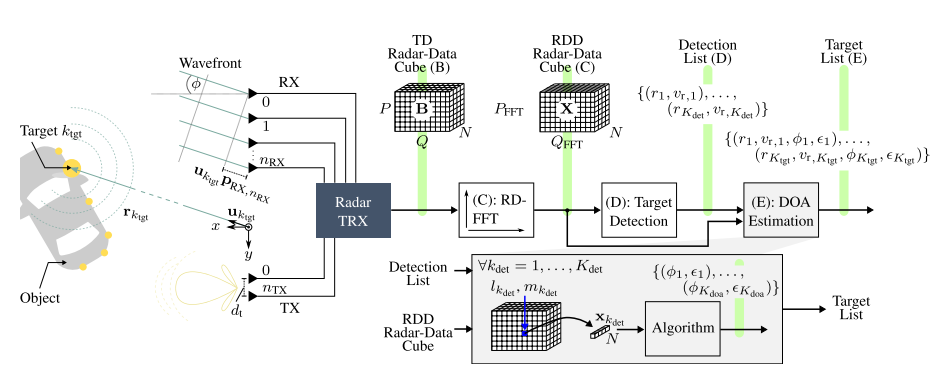
如图所示,雷达收发器(TRX)目前通常被实现为单个单片微波集成电路(MMIC)或甚至包括数字功能的片上系统(SoC),其生成雷达发射(TX)波形并经由连接到其TX信道的天线辐射该波形。电磁波通过空间传播,直到它命中一个或多个目标。假设目标的各向同性辐射,与目标雷达截面(RCS)成比例的入射波通量密度的一部分被捕获并朝向雷达再辐射。根据经典理论,目标通常被假设为孤立的点状散射体即点目标,如汽车、行人或环境之类的物理对象由若干点状目标组成,并且各个目标响应的总和则是总体接收(RX)信号。
通过比较雷达的TX和RX信号,可以估计出感知任务的基本参数:目标数目
\(K_{tgt}\)
和每个目标
\(k_{tgt}\)
的目标距离
\(r_{k_{tgt}}\)
,目标径向速度
\(v_{r_{k_{tgt}}}\)
,方位角
\(\phi_{k}\)
和俯仰角
\(\epsilon_k\)
。在每个测量周期中检测到的目标集合被称为目标列表,并且可以被解释为从雷达测量获得的点云。后续的毫米波雷达信号处理步骤主要有是聚类(即识别属于同一物理目标)、跟踪(即从目标列表的序列中导出物理上存在的对象的信息和统计数据)。
本章节的核心是介绍TDMA-MIMO框架下的信号模型仿真及实现方法。
本文所研究的模型与快速线性调频调频连续波(FMCW)雷达相关,这是目前智能驾驶、智能家居领域中所使用的主要雷达波形。如下图所示为典型的由Q个
chirp
组成的
chirp序列
构成的发射波形(绿色部分)和来自单个目标的接受波形信号(蓝色部分)。
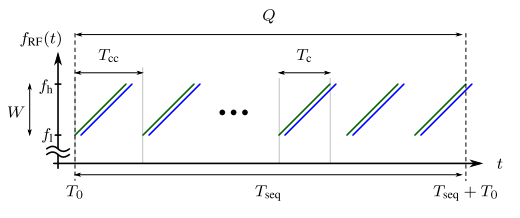
发射信号
\(s(t)\)
由以
chirp-chirp
间隔的为
\(T_{cc}\)
的
\(Q\)
个线性调频脉冲波形
\(s_c(t)\)
的序列给出:
\[s(t)=\sum\limits_{q=1}^Q s_{\mathrm{c}}(t-q T_{\mathrm{cc}})
\]
其中脉冲持续时间为
\(T_c\)
的每个
chirp
的信号表示为:
\[s_\mathrm{c}(t)=e^{j(2\pi f_1t+\pi\mu t^2+\varphi_0)}\mathrm{rect}\left(\frac{t-T_\mathrm{c}/2}{T_\mathrm{c}}\right).
\]
其中,
chirp
斜率为
\(\mu\)
,起始频率为
\(f_1\)
,截止频率为
\(f_h=f_l+W\)
,
\(W=\mu T_c\)
表示
chirp
的带宽,
chirp
的中心频率
\(f_c\)
定义为
\(f_1+W/2\)
,一帧
chirp
序列的长度或称帧周期为
\(T_{seq}=QT_{cc}-(T_{cc}-T_c)\)
。
每个点目标作为发射信号
\(s(t)\)
的时延副本以加权形式参与到接收信号
\(r(t)\)
中,其表示形式如下:
\[r(t)=\sum_{k_{t g t}=1}^{K_{t g t}}a_{k_{t g t}}s(t-T_{\mathrm{d},k}(t))
\]
其中,目标衰减系数
\(a_{k_{tgt}}\)
是由于自由空间传播和目标
RCS
引起的系数加权,往返时间
\(T_{d,k}(t)\)
是时间相关的,因为这考虑了目标的移动,通常帧周期为几毫秒或更小,与目标速度相比较短,无法形成积累效应。因此,
\(T_{\mathrm{d},k}(t))\)
可以近似表示为:
\[T_{\mathrm{d},k}(t)=\frac{2r_{k_\mathrm{tgt}}+2v_{r,k_\mathrm{tgt}}t}{c_0}.
\]
FMCW
雷达的基本原理是,发射信号
\(s(t)\)
和接收信号
\(r(t)\)
相乘混频,混频后通过低通滤波器
LPF
以滤除在和频(约两倍载波频率)处振荡的和分量,保留低通滤波信号即中频信号
IF Signal
,然后与发射信号定时同步地
ADC
采样。对于每个
chirp
,
ADC
采样将生成
P
个样本的向量,这意味着
\(Q\)
个线性调频脉冲的采样将生成
\(Q\)
个向量,并且每个向量长度为
\(P\)
,以二维矩阵
\({\mathcal{B}}=(b_{p,q}),{\mathcal{B}}\in{{\mathbb{C}}^{P\times Q}}\)
的形式存储,每个元素为
\(b_{p,q}\)
。
\(p\)
所在的维度称为快时间维,
\(q\)
所在的维度称为慢时间维度,这在上一节内容中已经提及。
基于所给的调制参数,可以将二维矩阵
\({\mathcal{B}}\)
的每个元素
\(b_{p,q}\)
展开如下:
\[b[p,q]\approx\sum_{k_1\mathfrak{g}=1}^{k_1}a_{k_1\mathfrak{g}n}e^{j(\lambda_{k_1\mathfrak{g}n}p+\zeta_{k_1\mathfrak{g}n}q)}e^{j\varphi_{k_1\mathfrak{g}n}}+\omega[p,q].
\]
其中,对应距离维度的归一化角频率可表示如下:
\[\lambda_{k_\mathrm{tgt}}=2\pi\left(\frac{2\mu r_{k_\mathrm{tgt}}}{c_0}+f_{\mathrm{d},k}\right)T_\mathrm{s},
\]
对应多普勒维度的归一化角频率可表示如下:
\[\xi_{k_{\mathrm{tgt}}}=2\pi\left(\frac{2f_{\mathrm{c}}v_{r,k_{\mathrm{tgt}}}}{c_{0}}\right)T_{\mathrm{cc}}
\]
目标的初始相位则可表示如下:
\[\varphi_{k_\mathrm{tgt}}=\frac{2f_c r_{k_\mathrm{tgt}}}{c_0}.
\]
空域信号模型
为了建立与目标方位角和仰角的关系,可以使用
\(N_{RX}\)
个接收天线的阵列,这将被称为单输入多输出(
SIMO
)配置;为了进一步提高角分辨率,在共同定位的相干
MIMO
配置中的若干发射和接收天线可用于现代毫米波雷达中,形成
\(N=N_{TX}N_{RX}\)
的虚拟接收阵列。
下图提供了一种基于三发四收的物理天线配置可能和
MIMO
后的虚拟阵列效果,左边天线标记为接收天线,右边天线标记为发射天线,可以很明显地看到
TX
和
TX1/TX2
在俯仰维度上存在偏移量,
RX2
和其他三根接收天线在俯仰维度上存在偏移量。
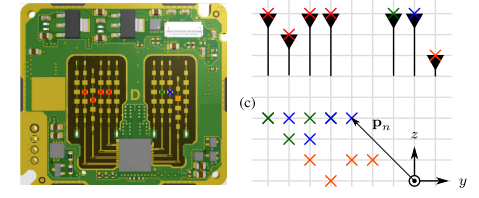
为更好地理解
MIMO
机制,下面将手把手推导如何得到虚拟阵列图(假设每个方格代表阵元间距
d
)。
TX1
在四根接收天线上形成的水平相位为
[0 w 2w 3w]
,俯仰相位为
[0 w 0 0]
TX2
在四根接收天线上形成的水平相位为
[w 2w 3w 4w]
,俯仰相位为
[0 w 0 0]
TX3
在四根接收天线上形成的水平相位为
[2w 3w 4w 5w]
,俯仰相位为
[2w 3w 2w 2w]
匹配上面的推导和下图中的右下边虚拟阵列,可以发现结果一致。这种推导在小阵列情况下容易实现,但是随着阵元数目的增加则容易出错,这是因为可能存在冗余阵元,如
TI AWR2243Cascade
具有12个发射天线和16个接收天线,实际在方位维度仅有86个虚拟阵元。为了排列准确,笔者写了以下程序来实现
物理阵元
到
虚拟阵列
的精确映射。
function cfgOut = ConfigureRTX()
% 下面这个程序实现了不同级联雷达的物理发射阵元和接收阵元配置,并考虑了天线发射顺序(这对虚拟阵元的排列影响不大,但会影响adc数据中的数据排列)。
% 实际的阵元间距可能与下面的存在误差,以下板子参数多为本人估算所得。
% 具体代码结合注释和上下文语句进行分析,这里不再赘述。
% By Xuliang
cfgOut.Mode = 4; % 选择需要仿真的雷达模式 这里提供了6种毫米波雷达配置,分别为TI
if cfgOut.Mode == 1
disp(strcat(['=====','已选择TI AWR1243-单板雷达模式','====='])); % 单板雷达模式3T4R
cfgOut.numTx = 3;
cfgOut.numRx = 4;
cfgOut.PosTX_X = [0 2 4]; % 发射天线水平方向阵元间距
cfgOut.PosTX_Y = [0 1 0]; % 发射天线垂直方向阵元间距
cfgOut.PosTX_BOARD_ID = [1 2 3]; % 发射天线板上顺序 后面没用到
cfgOut.PosTX_Trans_ID = [1 3 2]; % 发射天线发射顺序
cfgOut.PosRX_X = [0 1 2 3]; % 接收天线水平方向阵元间距
cfgOut.PosRX_Y = [0 0 0 0]; % 接收天线垂直方向阵元间距
cfgOut.PosRX_BOARD_ID = [1 2 3 4]; % 接收天线板上顺序
elseif cfgOut.Mode == 2
disp(strcat(['=====','已选择TI AWR2243-级联雷达模式','====='])); % 级联雷达模式12T16R
cfgOut.numTx = 12;
cfgOut.numRx = 16;
cfgOut.PosTX_X = [11 10 9 32 28 24 20 16 12 8 4 0];
cfgOut.PosTX_Y = [6 4 1 0 0 0 0 0 0 0 0 0];
cfgOut.PosTX_BOARD_ID = [12 11 10 3 2 1 9 8 7 6 5 4];
cfgOut.PosTX_Trans_ID = [12:-1:1];
cfgOut.PosRX_X = [11 12 13 14 50 51 52 53 46 47 48 49 0 1 2 3];
cfgOut.PosRX_Y = zeros(1,cfgOut.numRx);
cfgOut.PosRX_BOARD_ID = [13 14 15 16 1 2 3 4 9 10 11 12 5 6 7 8];
elseif cfgOut.Mode == 3 % 这个模式为特斯拉6T8R级联板
disp(strcat(['=====','已选择特斯拉6T8R-级联雷达模式','=====']));
cfgOut.numTx = 6;
cfgOut.numRx = 8;
cfgOut.PosTX_X = [0 17 34 41 48 55];
cfgOut.PosTX_Y = [0 0 0 0 4 8 12];
cfgOut.PosTX_BOARD_ID = [1 2 3 4 5 6];
cfgOut.PosTX_Trans_ID = [1 2 3 4 5 6];
cfgOut.PosRX_X = [0 2 3 5 8 11 14 17];
cfgOut.PosRX_Y = zeros(1,cfgOut.numRx);
cfgOut.PosRX_BOARD_ID = [1 2 3 4 5 6 7 8];
elseif cfgOut.Mode == 4 % 这个模式为加特兰 4T4R单板
disp(strcat(['=====','已选择加特兰4T4R-单板雷达模式','=====']));
cfgOut.numTx = 4;
cfgOut.numRx = 4;
cfgOut.PosTX_X = [0 5 12 18];
cfgOut.PosTX_Y = [5 0 0 0];
cfgOut.PosTX_BOARD_ID = [1 2 3 4];
cfgOut.PosTX_Trans_ID = [4 3 2 1];
cfgOut.PosRX_X = [0 2 5 7];
cfgOut.PosRX_Y = [0 0 0 2];
cfgOut.PosRX_BOARD_ID = [1 2 3 4];
elseif cfgOut.Mode == 5 % 这个模式为福瑞泰克 6T8R级联板
disp(strcat(['=====','已选择福瑞泰克6T8R-级联雷达模式','=====']));
cfgOut.numTx = 6;
cfgOut.numRx = 8;
cfgOut.PosTX_X = [0 2 4 6 8 10];
cfgOut.PosTX_Y = [0 0 0 0 0 0];
cfgOut.PosTX_BOARD_ID = [1 2 3 4 5 6];
cfgOut.PosTX_Trans_ID = [6 5 4 3 2 1];
cfgOut.PosRX_X = [0 2 5 13 13+ones(1,4)*1] + [0 0 0 0 0 2 5 13]; % 暂时不确定双级联间距
cfgOut.PosRX_Y = [1 0 0 0 1 0 0 0 0];
cfgOut.PosRX_BOARD_ID = [1 2 3 4 5 6 7 8];
elseif cfgOut.Mode == 6 % 这个模式为TI双级联毫米波雷达
disp(strcat(['=====','已选择TI 6T8R-级联雷达模式','=====']));
cfgOut.numTx = 6;
cfgOut.numRx = 8;
cfgOut.PosTX_X = [0 2 4 7 11 15];
cfgOut.PosTX_Y = [0 1.6 0 0 0 0];
cfgOut.PosTX_BOARD_ID = [1 3 2 4 5 6];
cfgOut.PosTX_Trans_ID = [6 5 4 3 2 1];
cfgOut.PosRX_X = [0 1 2 3 19 20 21 22];
cfgOut.PosRX_Y = [0 0 0 0 0 0 0 0 0];
cfgOut.PosRX_BOARD_ID = [1 2 3 4 5 6 7 8];
end
virtual_azi_arr = repmat(cfgOut.PosTX_X(cfgOut.PosTX_Trans_ID), cfgOut.numRx, 1) + repmat(cfgOut.PosRX_X(cfgOut.PosRX_BOARD_ID), cfgOut.numTx, 1).';
virtual_ele_arr = repmat(cfgOut.PosTX_Y(cfgOut.PosTX_Trans_ID), cfgOut.numRx, 1) + repmat(cfgOut.PosRX_Y(cfgOut.PosRX_BOARD_ID), cfgOut.numTx, 1).';
virtual_array.azi_arr = reshape(virtual_azi_arr,[],1);
virtual_array.ele_arr = reshape(virtual_ele_arr,[],1);
virtual_array.tx_id = reshape(repmat(cfgOut.PosTX_Trans_ID, cfgOut.numRx, 1),[],1);
virtual_array.rx_id = reshape(repmat(cfgOut.PosRX_BOARD_ID, cfgOut.numTx, 1).',[],1);
virtual_array.virtual_arr = cat(2,virtual_array.azi_arr,virtual_array.ele_arr,virtual_array.rx_id,virtual_array.tx_id);
cfgOut.virtual_array = virtual_array; % 将virtual_array参数存入更新
end
% 测试文件:可视化虚拟阵元排列
% By Xuliang
clc;clear;close all
cfgOut = ConfigureRTX();
plot(cfgOut.virtual_array.virtual_arr(:,1), cfgOut.virtual_array.virtual_arr(:,2),'ro');
xlabel('方位维');ylabel('俯仰维');grid minor;
% 这里不再进行可视化。
在上一章节中,我们可以得到单信道下的时域信号模型为
\(b[p,q]\approx\sum_{k_1\mathfrak{g}=1}^{k_1}a_{k_1\mathfrak{g}n}e^{j(\lambda_{k_1\mathfrak{g}n}p+\zeta_{k_1\mathfrak{g}n}q)}e^{j\varphi_{k_1\mathfrak{g}n}}+\omega[p,q].\)
$
假设目标满足远场窄带信号假设,那么可进一步扩展时域信号至空域信号如下:
\[b[p,q,n]\approx\sum_{k\text{g}s=1}^{K_\text{g}t}a_{k\text{g}t}e^{i(\lambda_{k\text{g}t}p+\zeta_{k\text{g}s}q)}e^{i\varphi_{k\text{g}t}}e^{j\frac{2\pi}{\lambda}(\mathfrak{u}_{k\text{g}s}\mathfrak{p}_n)}+\omega[p,q,n].
\]
上述信号对应于雷达
3D tensor
或
radar cube
数据的元素,根据
ISO8000:2标准
定义的球面坐标系,目标
\(k_{tgt}\)
对应的单位长度波达角矢量可以表示如下:
\[\mathbf{u}_k=\mathbf{r}_{k_\textrm{tgt}}/\|\mathbf{r}_{k_\textrm{tgt}}\|=\begin{bmatrix}\cos\phi_{k_\textrm{tgt}}\sin\theta_{k_\textrm{t}}\\ \sin\phi_{k_\textrm{gt}}\sin\theta_{k_\textrm{tgt}}\\ \cos\theta_{k_\textrm{tgt}}\end{bmatrix}
\]
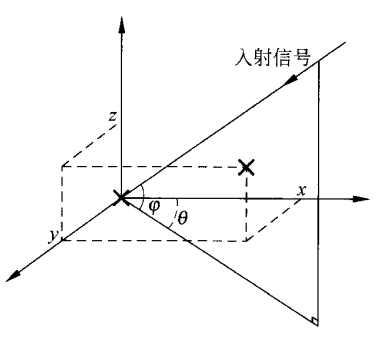
其中,
\(\phi_{k_\textrm{tgt}}\)
和
\(\theta_{k_\textrm{tgt}}\)
分别表示目标的方位角和倾斜角,俯仰角则表示为
\(\epsilon_{k_{tgt}}=\pi-\theta_{k_{tgt}}\)
;虚拟天线的位置
\(p_n\)
可以表示如下(
\(n=0....N-1\)
)
\[\mathbf{p}_n=\mathbf{p}_{\mathrm{RX},n_{\mathrm{RX}}}+\mathbf{p}_{\mathrm{TX},n_{\mathrm{TX}}},n_{\mathrm{RX}}=n\bmod N_{\mathrm{RX}},\quad n_{\mathrm{TX}}=n\bmod N_{\mathrm{TX}}
\]
至此,我们可以很明确地建立目标角度和模型
\(e^{(2\pi/\lambda)\mathbf{u}_{k_\mathrm{tgt}}\mathbf{p}_n}\)
有关,上面提到的目标初始相位
\(\varphi_{k_\mathrm{tgt}}=\frac{2f_c r_{k_\mathrm{tgt}}}{c_0}\)
可以衡量目标在参考坐标系原点处出现的相位,不大影响角度的估计。
基于以上信号模型,我们可以生成
TDMAI-MIMO
下的
radar cube
数据文件,核心代码如下所示:
function [signal] = GenerateSigIQ(tarOut, cfgOut)
%% 本文件用于毫米波雷达的ADC-IQ信号
%% By Xuliang
tarNum = tarOut.nums; % 目标数目
numTx = cfgOut.numTx; % 发射天线数目
numRx = cfgOut.numRx; % 接收天线数目
ADCNum = cfgOut.ADCNum; % ADC采样数目
Frame = cfgOut.Frame; % 帧数
ChirpNum = cfgOut.ChirpNum; % 每帧发射Chirp数目
TotalChirpNum = Frame * ChirpNum; % 总Chirp数目
% 信号参数
fc = cfgOut.fc; % 载频 Hz
fs = cfgOut.fs; % ADC采样频率 Hz
Ramptime = cfgOut.Ramptime; % 工作时间
Idletime = cfgOut.Idletime; % 空闲时间
Slope = cfgOut.Slope; % Chirp斜率
validB = cfgOut.validB; % 实际有效带宽
totalB = cfgOut.totalB; % 完整带宽
Tc = cfgOut.Tc; % 单Chirp周期
ValidTc = cfgOut.ValidTc; % 单Chirp内ADC有效采样时间
% 硬件参数
Pt = cfgOut.Pt; % dbm 发射功率
Fn = cfgOut.Fn; % 噪声系数
Ls = cfgOut.Ls; % 系统损耗
% 天线阵列
antennaPhase = cfgOut.antennaPhase; % 天线相位
virtual_array = cfgOut.virtual_array; % 虚拟阵列 这里的虚拟阵列是struct virtual_arr中包含了发射方位相位和俯仰相位 接收天线 发射天线顺序
arr = virtual_array.virtual_arr;
% 初阶版本顺序发射可行
% arr = cfgOut.array; % 虚拟阵元排列
arrNum = size(arr, 1); % 虚拟阵列数目
arrdelay = zeros(1, arrNum) + Tc * reshape(repmat([0:numTx-1], numRx,1), 1, arrNum); % [0 0 0 0 1 1 1 1 2 2 2 2]
% arrdelay = zeros(1, arrNum); % 这一项相当于常数项 本来考虑的是天线间时延
delayTx = Tc * numTx; % 发射天线维度积累的时延
arrdx = cfgOut.arrdx; % 归一化阵元间距
arrdy = cfgOut.arrdy;
c = physconst('LightSpeed'); % 光速
lambda = c / fc; % 波长
Ts = 1 / fs; % ADC采样时间
% 信号模型
signal = zeros(ADCNum, TotalChirpNum, arrNum); % 信号
noiseI = normrnd(0, 1, ADCNum, TotalChirpNum, arrNum); % 正态噪声
noiseQ = normrnd(0, 1, ADCNum, TotalChirpNum, arrNum); % 正态噪声
% noiseI = exprnd(1, ADCNum, TotalChirpNum, arrNum); % 指数分布噪声
% noiseQ = exprnd(1, ADCNum, TotalChirpNum, arrNum); % 指数分布噪声
for tarId = 1 : tarNum
disp(strcat(['正在获取目标',num2str(tarId),'的数据']));
% 目标参数
targetR = tarOut.range(tarId); % 距离 m
targetV = tarOut.velocity(tarId); % 速度 m/s
targetAzi = tarOut.Azi(tarId); % 目标方位角 度
targetEle = tarOut.Ele(tarId); % 目标俯仰角 度
targetRCS = tarOut.RCS(tarId); % 目标RCS值
targetGt = tarOut.Gt(tarId); % 发射增益
targetGr = tarOut.Gr(tarId); % 接收增益
[tarSNR] = CalculateSNR(targetR, targetRCS, targetGt, targetGr, lambda, Pt, Fn, Ls, validB); % 信噪比
A = sqrt(2 * db2pow(tarSNR)); % 信号幅度
targPhi0 = rand * 2 * pi; % 产生随机相位[0 2*pi] 这里的目标初始相位也可以根据上面定义的形式来写 但影响不大
tempSigI = zeros(ADCNum, TotalChirpNum, arrNum); % I路缓存信号
tempSigQ = zeros(ADCNum, TotalChirpNum, arrNum); % Q路缓存信号
tempSig = zeros(ADCNum, TotalChirpNum, arrNum); % I路缓存信号
for channelId = 1 : arrNum
for chirpId = 1 : TotalChirpNum
for adcId = 1 : ADCNum
% 动目标时延
tarDelay = 2 * targetR / c + 2 * targetV * ((chirpId - 1) * delayTx + arrdelay(channelId) + adcId * Ts) / c;
% 控制来波方向
% 初阶版本的目标相位表达
% tarPhi = targPhi0 + 2 * pi * (arr(1, channelId) * sind(targetAzi) * arrdx + ...
% arr(2, channelId) * sind(targetEle) * arrdy) + deg2rad(antennaPhase(channelId)); % 考虑阵元初始、随机相位和目标波达角
% tarPhi0 = 2 * targetR * fc / c; % 目标初始相位 也可以用随机相位
tarPhi = targPhi0 + 2 * pi * (arr(channelId) * sind(targetAzi) * arrdx + ...
arr(arrNum+channelId) * sind(targetEle) * arrdy) + deg2rad(antennaPhase(channelId)); % 这里考虑了不同发射顺序天线相位
% 中频信号:exp[1j * 2 *pi * fc * tau + 2 * pi * S * t * tau - pi * tau * tau] t的范围为0-Tc tau的范围为t+nTc
tempSigI(adcId, chirpId, channelId) = A * cos(2 * pi * (fc * tarDelay + Slope * tarDelay * adcId * Ts - Slope * tarDelay * tarDelay / 2) + tarPhi);
tempSigQ(adcId, chirpId, channelId) = A * sin(2 * pi * (fc * tarDelay + Slope * tarDelay * adcId * Ts - Slope * tarDelay * tarDelay / 2) + tarPhi);
tempSig(adcId, chirpId, channelId) = tempSigI(adcId, chirpId, channelId) + 1j * tempSigQ(adcId, chirpId, channelId);
end
end
end
signal = signal + tempSig; % 多目标信号相加
end
signal = signal - (noiseI + noiseQ); % 考虑噪声
% signal = reshape(signal, size(signal,1), size(signal,2), numRx, numTx);
end
信号处理栈
在上一章节,我们已经得到了
radar cube
数据,这个数据和毫米波雷达
ADC
数据是异曲同工的。那么,针对现有数据可以展开信号处理栈的分析,简言之,传统的信号处理栈为
RDA
,如本文开篇的图所示。
首先,沿着
radar cube
数据的快时间和慢时间维度分别使用FFT(快速傅立叶变换)的到距离多普勒域数据
RDD
,这可以表示为如下形式:
\[x_n(\lambda,\zeta)=\sum_{k_{tgt}=1}^{K_\text{tgt}}a_{k_{tgt}}{k_{tgt}}W_{\text{ft}}(\lambda-\lambda_{k_{tgt}})W_{\text{st}}(\zeta-\zeta_{k_{tgt}})e^{j\varphi_{k_{tgt}}}\cdot e^{j\frac{2\pi}{\lambda}(\mathbf{u}_{k\mathrm{tgt}}\cdot\mathbf{p}_n)}+\Omega_n(\lambda,\zeta)
\]
其中
\(W_{ft}(\lambda)\)
和
\(W_{st}(\zeta)\)
分别表示在快时间和慢时间维度上应用的窗函数傅里叶变换,这实现了信号移位至目标对应的距离维和多普勒峰值频率处:
\(\lambda_{k_{tgt}}\)
和
\(\zeta_{k_{tgt}}\)
。目标初始相位项
\(e^{j\varphi_{k_{tgt}}}\)
和相位分布项
\(e^{j\frac{2\pi}{\lambda}(\mathbf{u}_{k\mathrm{tgt}}\cdot\mathbf{p}_n)}\)
保持不变,这是因为沿距离-多普勒维度的傅里叶变换并不影响天线维度的相位信息。
\(\Omega_n(\lambda,\zeta)\)
则表示频域噪声。
为了进一步对距离-多普勒变换后的信号处理,将上述混合信号表示为如下形式:
设距离多普勒域的
radar cube
的元素为
\(x_{l,m,n}~~=~~x[l,m,n]\)
,快时间和慢时间维度的FFT点数对应
\({P_{\mathrm{FFT}}}\)
和
\({Q_{\mathrm{FFT}}}\)
\[\lambda=\frac{2\pi}{P_{\mathrm{FFT}}}l,\quad\zeta=\frac{2\pi}{Q_{\mathrm{FFT}}}m,\quad x[l,m,n]=x_n\left(\frac{2\pi}{P_{\mathrm{FFT}}}l,\frac{2\pi}{Q_{\mathrm{FFT}}}m\right).
\]
其次,我们需要对距离-多普勒域的
radar cube
进行目标检测,这通常用恒虚警率检测算法(
cfar, constant false alarm rate
)来实现,在正式进行检测前,我们需要对
radar cube
沿天线维度展开,通常可以选择一个天线通道对应的距离多普勒数据或使用所有天线通道的距离多普勒数据进行非相干积累处理(波束成形)得到
cfar
检测输入数据,这个过程可以表示如下:(下面第一式为方法1,第二式为方法2,
\(N_{det}\)
为单天线通道,
\(N^\prime\)
为全部天线通道)
\[X^\prime=|x'[l,m]|^2=|x[l,m,n=N_{\det}]|^2
\]
\[X^\prime=|x'[l,m]|^2=\sum\limits_{n\in N'}|x[l,m,n]|^2
\]
那么,现在我们可以对处理后的距离多普勒矩阵
\(X^\prime\)
进行
cfar
检测。通常,
cfar
检测针对数据维度可以分为
1D-cfar
和
2D-cfar
,针对处理思想可以分为
均值类、有序统计类、自动筛选类和自适应类
(这部分详细细节可以参考
何友院士和关键老师
的
雷达目标检测与恒虚警处理
书,后续会整理我的
本科毕设
中关于这方面的内容)。实际上,我们可以考虑两次
1D-CFAR
即对距离多普勒矩阵
\(X^\prime\)
的距离和多普勒维度分别作
cfar
并关联匹配目标,或者考虑1次
2d-cfar
即直接在二维距离多普勒矩阵
\(X^\prime\)
上作二维检测,这里我们主要用
2d-cfar
来检测目标。
在下面我们通过
2D-CFAR
示意图来更好地理解原理。浅蓝色单元构成的大矩形区域为输入的距离-多普勒矩阵
\(X^\prime\)
深红色单元为检测单元,浅红色单元为保护单元(防止旁瓣能量信号泄露主瓣形成掩蔽效应),浅绿色为参考单元,由深红色单元、浅红色单元和浅绿色单元构成的小矩形区域作为滑动窗窗;依次移动滑动窗在大矩形区域内遍历检测目标,移动过程中需要保证检测单元的中心
从黄色的起始中心单元
开始依次完成自左向右、自上而下的二维扫描,直至完成整个大矩形区域的遍历。【注意到,我们在这里强调了
"从黄色的起始中心单元"
,这部分需要在程序中重点处理,否则可能会导致部分区域是没有参与检测的。】
以单元平均恒虚警检测算法(
ca-cfar,cell-averaging cfar
)为例,首先需要根据预设虚警概率和滑动窗尺寸等先验参数计算门限因子
\(\alpha\)
;在每次扫描中,需求求解参考窗内所有检测单元对应的信号电平的和并取平均值,这一估计值可以表示为
\(\bar{X}\)
,将估计阈值
\(\bar{X}\cdot \alpha\)
和检测单元下的信号电平进行比较,如果检测单元下信号电平大于估计阈值
\(\bar{X}\cdot \alpha\)
,则认为检测单元出为目标信号,否则认为噪声信号。
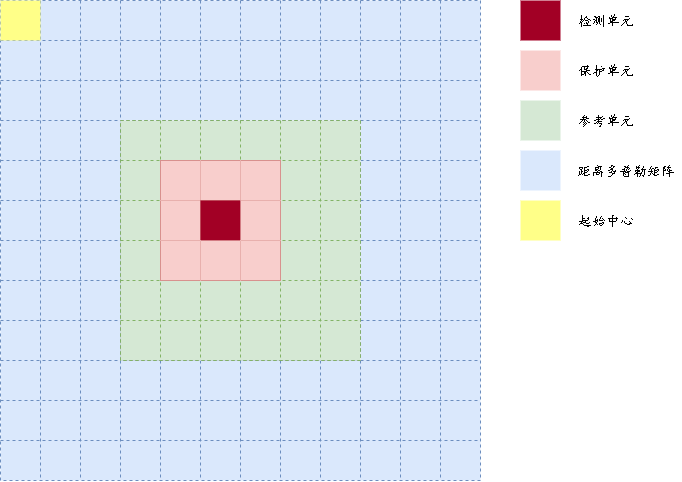
在这里我们通过以下程序来更好地帮助理解
2d-cfar
过程:
function [cfarOut] = CFAR_2D(RDM, Pfa, TestCells, GuardCells)
% rd_map:输入数据
% Pfa:虚警概率
% TestCells:测试单元 [4 4]
% GuardCells:保护单元 [4 4]
% By Xuliang
% CFAR检测器
detector = phased.CFARDetector2D('TrainingBandSize',TestCells, ...
'ThresholdFactor','Auto','GuardBandSize',GuardCells, ...
'ProbabilityFalseAlarm',Pfa,'Method','SOCA','ThresholdOutputPort',true, 'NoisePowerOutputPort',true);
N_x = size(RDM,1); % 距离单元
N_y = size(RDM,2); % 多普勒单元
% 获取二维滑动窗口的size
Ngc = detector.GuardBandSize(2); % 保护窗列向
Ngr = detector.GuardBandSize(1); % 保护窗行向
Ntc = detector.TrainingBandSize(2); % 参考窗行向
Ntr = detector.TrainingBandSize(1); % 参考窗行向
cutidx = [];
colstart = Ntc + Ngc + 1; % 列窗首
colend = N_y + ( Ntc + Ngc); % 列窗尾
rowstart = Ntr + Ngr + 1; % 行窗首
rowend = N_x + ( Ntr + Ngr); % 行窗尾
for m = colstart:colend
for n = rowstart:rowend
cutidx = [cutidx,[n;m]]; % 完整二维窗
end
end
ncutcells = size(cutidx,2); % 获取窗口遍历区间
rd_map_padding = repmat(RDM, 3, 3); % 对RDM补零
chosen_rd_map = rd_map_padding(N_x+1-Ntr-Ngr:2*N_x+Ntr+Ngr,N_y+1-Ntc-Ngc:2*N_y+Ntc+Ngc);
[dets, ~, noise] = detector(chosen_rd_map,cutidx); % 输出CFAR结果
cfar_out = zeros(size(chosen_rd_map)); % 检测点输出
noise_out = zeros(size(chosen_rd_map)); % 噪声
snr_out = zeros(size(chosen_rd_map)); % 信噪比
for k = 1:size(dets,1)
if dets(k) == 1
cfar_out(cutidx(1,k),cutidx(2,k)) = dets(k);
noise_out(cutidx(1,k),cutidx(2,k)) = noise(k);
snr_out(cutidx(1,k),cutidx(2,k)) = chosen_rd_map(cutidx(1,k),cutidx(2,k));
end
end
cfarOut = {};
cfarOut.cfarMap = cfar_out(Ntr+Ngr+1:Ntr+Ngr+N_x,Ntc+Ngc+1:Ntc+Ngc+N_y);
cfarOut.snrOut = snr_out(Ntr+Ngr+1:Ntr+Ngr+N_x,Ntc+Ngc+1:Ntc+Ngc+N_y);
cfarOut.noiseOut = noise_out(Ntr+Ngr+1:Ntr+Ngr+N_x,Ntc+Ngc+1:Ntc+Ngc+N_y);
cfarOut.snrOut = cfarOut.snrOut ./ (eps + cfarOut.noiseOut);
end
经过
cfar
检测后,我们可以得到一组由
\(K_{det}\)
个检测目标构成的集合:
\[\mathrm{cfar}\left(\left|x'[l,m]\right|^2\right)=\{(r_1,v_{\mathrm{r},1}),(r_2,v_{\mathrm{r},2}),\ldots,(r_{k_{\det}},v_{\mathrm r,k_{\det}}),\ldots,(r_{K_{\det}},v_{\mathrm r,K_{\det}})\}
\]
其中,每个检测目标由与其关联的参数元组进行表示,每个参数元组
\((r_{K_{\det}},v_{\mathrm r,K_{\det}})\)
中包含了目标的距离和速度,这可以通过距离或多普勒维度的峰值索引通过物理映射实现距离和速度解析,这里需要用到距离分辨率和速度分辨率的概念(可以阅读先前的博文进行回顾)。
下面,我们可以进入
doa
估计;不过我们需要准备好用于空间谱估计的输入信号,这需要用到由上面缓存的
radar cube
数据和经过
cfar
检测得到的目标距离-速度集合
\(\mathrm{cfar}\left(\left|x'[l,m]\right|^2\right)\)
来提取空域信号
\(\mathbf{x}_{k\mathrm{det}}\)
,表示如下:(
\(N\)
表示阵元数目)
\[\mathbf{x}_{k\mathrm{det}}=x[l_{k\mathrm{det}},m_{k\mathrm{det}},n]=[x_0,\ldots,x_{N-1}]^T
\]
基于经过距离多普勒FFT的混合信号模型
\(x_n(\lambda,\zeta)\)
,我们可以建立空域信号模型为:
\[\mathbf{x}_{k_{\det}}=\sum_{k_{\text{doa}}=1}^{K_{\text{doa}}}s_{k_{\text{doa}}}\mathbf{a}(\phi_{k_{\text{doa}}},\epsilon_{k_{\text{doa}}})+\boldsymbol{\omega}
\]
不难发现上述信号表示是标准的空间谱估计信号模型
X=AS+N
,其中
A
为流形,
S
为信号空间,
N
为噪声空间(上面用
\(\omega\)
表示噪声项,通常假设满足复高斯白噪声分布),
X
为观测空间;在这里,我们也可以将
A
视为完备基或字典,字典原子或称导向矢量
\(\mathbf{a}(\phi_{k_{\text{doa}}},\epsilon_{k_{\text{doa}}})\)
满足线性无关,那么目标的来波信号可以由字典中的原子通过复权重
\(s_{k_{doa}}\)
加权得到,导向矢量和复权重的表示分布如下:
\[\mathbf{a}(\phi_{k_\text{doa}},\epsilon_{k_\text{doa}})=e^{j(2\pi/\lambda)\mathbf{u}_{k_\text{doa}}\mathbf{p}_n}
\]
\[s_{k\text{doa}}=a_{k\text{doa}}W_{\text{ft}}(\lambda-\lambda_{k\text{doa}})W_{\text{st}}(\zeta-\zeta_{k\text{doa}})e^{j\varphi_{k}\text{doa}}
\]
doa
估计的本意是在给定峰值目标空域信号
\(\mathbf{x}_{k\mathrm{det}}\)
和阵列集合结构
\(p_n\)
的基础上估计出目标数目
\(K_{doa}\)
、目标来波方向
\(\phi_{k_{doa}}\)
和
\(\epsilon_{k_{doa}}\)
,即如下目标:
\((r_{k_\mathrm{det}},v_{\mathrm{r},k_\mathrm{det}},\mathbf{x}_{k_\mathrm{det}})\to(r_{k_\mathrm{tgt}},v_{r,k_\mathrm{tgt}},\phi_{k_\mathrm{tgt}},\epsilon_{k_\mathrm{tgt}})\)
。在本处,我们可以对上述阵列信号完成对应维度的天线映射后,首先对方位天线维度做FFT处理,并认为方位维空间最大谱峰所在处为对应的目标方位角;其次,基于目标方位天线的峰值索引,我们沿其俯仰维度做FFT处理,并认为俯仰维空间最大谱峰所在处为对应的目标俯仰角,以此实现目标信号方位和俯仰维度的匹配关联。这种方法可以理解为“两步走”战略,和上面提及的两次
1D-CFAR
是类似的。
当然,我们也可以使用波束成形
CBF
、线性滤波
Capon
、子空间方法(
MUSIC
,
ESPRIT
,
DML
等)和压缩感知方法(
OMP
,
IAA
和
LISTA
等),这些内容我们将在后面的章节中讨论,在这里需要注意一点,我们要保证方位天线维度上的空间谱估计不能够破坏俯仰天线维度观测信号的相位信息,否则会导致俯仰角的估计错误。
至此,我们已经基本完成了
RDA
信号处理栈的基本物理量提取并最终得到
点云
表示
\((r_{k_\mathrm{tgt}},v_{r,k_\mathrm{tgt}},\phi_{k_\mathrm{tgt}},\epsilon_{k_\mathrm{tgt}})\)
。所述过程仍存在一些细节性内容没有解释,这部分可以结合代码更好地去理解,下面给出核心信号处理实现部分。
for frame_id = 1 : Frame % Frame
adcData = squeeze(RawData(:, :, frame_id, :));
%% 距离维FFT和多普勒FFT
disp(strcat(['=====','RD-MAP生成','=====']));
tic
fftOut = rdFFT(adcData, IQFlag);
toc
rangeFFTOut = fftOut.rangeFFT;
dopplerFFTOut = fftOut.dopplerFFT;
if ShowRange
figure(2);
set(gcf,'unit','centimeters','position',[10,0,10,10])
plot(rangeIndex, db(rangeFFTOut(:,1,1)));
xlabel('Range(m)');ylabel('Amplitude(dB)');
title(strcat(['第',num2str(frame_id),'帧-目标距离分布']));grid minor;
pause(0.1);
end
if ShowRD
figure(3);
set(gcf,'unit','centimeters','position',[20,12,10,10])
imagesc(rangeIndex, velocityIndex, db(dopplerFFTOut(:,:,1).'));
xlabel('Range(m)');ylabel('Velocity(m/s)'); colormap('jet');
title(strcat(['第',num2str(frame_id),'帧目标-距离多普勒分布']));
grid minor; axis xy;
pause(0.1);
end
%% 非相干积累
disp(strcat(['=====','非相干积累','=====']));
RDM = dopplerFFTOut;
tic
[accumulateRD] = incoherent_accumulation(RDM);
toc
%% CFAR检测器
disp(strcat(['=====','恒虚警检测','=====']));
Pfa = 1e-3; % 虚警概率
TestCells = [8, 8]; % 参考窗
GuardCells = [2, 2]; % 保护窗
tic
[cfarOut] = CFAR_2D(accumulateRD, Pfa, TestCells, GuardCells);
toc
cfarMap = cfarOut.cfarMap; % 检测点输出
noiseOut = cfarOut.noiseOut; % 噪声输出
snrOut = cfarOut.snrOut; % 信噪比输出
if ShowCFAR
figure(4);
set(gcf,'unit','centimeters','position',[20,0,10,10])
imagesc(rangeIndex, velocityIndex, cfarMap.');
xlabel('Range(m)');ylabel('Velocity(m/s)'); colormap('jet');
title(strcat(['第',num2str(frame_id),'帧目标-CFAR检测结果']));
grid minor;axis xy;
pause(0.1);
end
%% 峰值聚合-获取点目标
disp(strcat(['=====','峰值聚合','=====']));
[range_idx, doppler_idx] = find(cfarMap);
cfar_out_idx = [range_idx doppler_idx]; % 获取CFAR输出结果的行列索引
tic
[rd_peak_list, rd_peak] = peakFocus(db(accumulateRD), cfar_out_idx);
toc
peakMap = zeros(size(cfarMap)); % 峰值聚合结果矩阵
for peak_idx = 1 :size(rd_peak_list, 2)
peakMap(rd_peak_list(1,peak_idx), rd_peak_list(2,peak_idx)) = 1;
end
if ShowPeak
figure(5);
set(gcf,'unit','centimeters','position',[30,12,10,10])
imagesc(rangeIndex, velocityIndex, peakMap.');
xlabel('Range(m)');ylabel('Velocity(m/s)'); colormap('jet');
title(strcat(['第',num2str(frame_id),'帧目标-峰值聚合结果']));
grid minor;axis xy;
pause(0.1);
end
%% DOA/AOA估计
disp(strcat(['=====','DOA/AOA估计','=====']));
cfgDOA.FFTNum = 180; % FFT点数
% 这里虽然封装了不同的DOA算法 但是需要注意的是 可用的算法有限 在本套代码里 建议使用的是FFT-FFT和FFT-MUSIC等
% 因为MUSIC-MUSIC的使用会导致在方位维度空间谱估计时破坏相位信号 有损俯仰维度的相位估计
cfgDOA.AziMethod = 'FFT'; % 方位维度DOA估计方法
cfgDOA.EleMethod = 'MUSIC'; % 俯仰维度DOA估计方法
cfgDOA.thetaGrids = linspace(-90, 90, cfgDOA.FFTNum); % 空间网格
cfgDOA.AzisigNum = 1; % 约束每个RD-CELL上的信源数目
cfgDOA.ElesigNum = 1; % 约束每个方位谱峰上的信源数目
aziNum = length(virtual_array.noredundant_aziarr); % 方位天线数目
% Aset = exp(-1j * 2 * pi * arrDx * [0:aziNum]' * sind(cfgDOA.thetaGrids)); % 稀疏字典设计
targetPerFrame = {};
targetPerFrame.rangeSet = [];
targetPerFrame.velocitySet = [];
targetPerFrame.snrSet = [];
targetPerFrame.azimuthSet = [];
targetPerFrame.elevationSet = [];
if ~isempty(rd_peak_list) % 非空表示检测到目标
rangeVal = (rd_peak_list(1, :) - 1) * range_res; % 目标距离
speedVal = (rd_peak_list(2, :) - ChirpNum / 2 - 1) * doppler_res; % 目标速度
doaInput = zeros(size(rd_peak_list, 2), arrNum);
for tar_idx = 1 :size(rd_peak_list, 2)
doaInput(tar_idx, :) = squeeze(dopplerFFTOut(rd_peak_list(1, tar_idx), rd_peak_list(2, tar_idx), :)); % tarNum * arrNum
end
doaInput = reshape(doaInput, [], numRx, numTx);
% 方位角估计前需要考虑多普勒补偿
[com_dopplerFFTOut] = compensate_doppler(doaInput, cfgOut, rd_peak_list(2, :), speedVal, rangeVal);
tic
for peak_idx = 1 : size(rd_peak_list, 2) % 遍历检测到的每个目标
snrVal = mag2db(snrOut(rd_peak_list(1, peak_idx), rd_peak_list(2, peak_idx))); % 信噪比的提升是由于chirpNum*ADCNum的积累
tarData = squeeze(com_dopplerFFTOut(peak_idx, :,:));
% aziarr = unique(arr(1,arr(2,:)==0)); % 初阶版本获取方位维度天线排列
% aziArrData = arrData(aziarr+1); % 获取方位维度信号
% 方位角解析
sig = tarData;
sig_space = zeros(max(virtual_array.azi_arr)+1,max(virtual_array.ele_arr)+1); % 初始化信号子空间
for trx_id = 1 : size(cfgOut.sigIdx,2)
sig_space(cfgOut.sigSpaceIdx(1, trx_id), cfgOut.sigSpaceIdx(2,trx_id)) = sig(cfgOut.sigIdx(1,trx_id), cfgOut.sigIdx(2,trx_id)); % 重排后的信号空间
end
% 至此我们生成的信号子空间维度为 方位虚拟天线数目 * 俯仰虚拟天线数目
eleArrData = zeros(cfgDOA.FFTNum, size(sig_space,2)); % 俯仰维度数据
for ele_idx = 1 : size(sig_space, 2) % 这里采取遍历是为了适配不同的空间谱估计方法
tmpAziData = sig_space(:, ele_idx);
[azidoaOut] = azimuthDOA(tmpAziData, cfgDOA); % 提取第一列方位维度天线信息进行方位角估计
eleArrData(:, ele_idx) = azidoaOut.spectrum(:); % 复空间谱
end
for azi_peak_idx = 1 : length(azidoaOut.angleVal) % 对方位维度检测的谱峰进行检索
tmpEleData = eleArrData(azidoaOut.angleIdx(azi_peak_idx), :).'; % 获取与方位维目标关联的信号
[eledoaOut] = elevationDOA(tmpEleData, cfgDOA); % 进行俯仰角估计
% 关联目标的距离、多普勒、信噪比、方位和俯仰信息
aziVal = azidoaOut.angleVal;
eleVal = eledoaOut.angleVal;
targetPerFrame.rangeSet = [targetPerFrame.rangeSet, rangeVal(peak_idx)];
targetPerFrame.velocitySet = [targetPerFrame.velocitySet, speedVal(peak_idx)];
targetPerFrame.snrSet = [targetPerFrame.snrSet, snrVal];
targetPerFrame.azimuthSet = [targetPerFrame.azimuthSet,aziVal];
targetPerFrame.elevationSet = [targetPerFrame.elevationSet,eleVal];
end
end
toc
%% 点云生成
disp(strcat(['=====','点云生成','=====']));
tic
pcd_x = targetPerFrame.rangeSet .* cosd(targetPerFrame.elevationSet) .* sind(targetPerFrame.azimuthSet);
pcd_y = targetPerFrame.rangeSet .* cosd(targetPerFrame.elevationSet) .* cosd(targetPerFrame.azimuthSet);
pcd_z = targetPerFrame.rangeSet .* sind(targetPerFrame.elevationSet);
PointSet = [pcd_x.', pcd_y.', pcd_z.', targetPerFrame.velocitySet.', targetPerFrame.snrSet.'];
toc
%% 点云聚类
eps = 1.1; % 邻域半径
minPointsInCluster = 3; % 簇内最小点数阈值
xFactor = 1; % 变大控制距离变大,变小分类距离变小 椭圆
yFactor = 1; % 变大控制角度变大,变小分类距离变小 椭圆
figure(6);
set(gcf,'unit','centimeters','position',[30,0,10,10])
disp(strcat(['=====','点云聚类','=====']));
tic
[sumClu] = dbscanClustering(eps,PointSet,xFactor,yFactor,minPointsInCluster,frame_id); % DBSCAN聚类
toc
end
end
在本文的尾巴,本文将展示本程序所实现的可视化功能。在以下仿真中,目标距离为
[5 10 15 18]
,目标速度为
[0.4 -0.3 0 0.6]
,目标方位角为
[15 -2 30 -25]
,目标俯仰角为
[0 15 -5 8]
,目标RCS为
[20 20 10 20]
,仿真实验平台为
TI AWR1243BOOST
,其他平台均可实现类似效果。
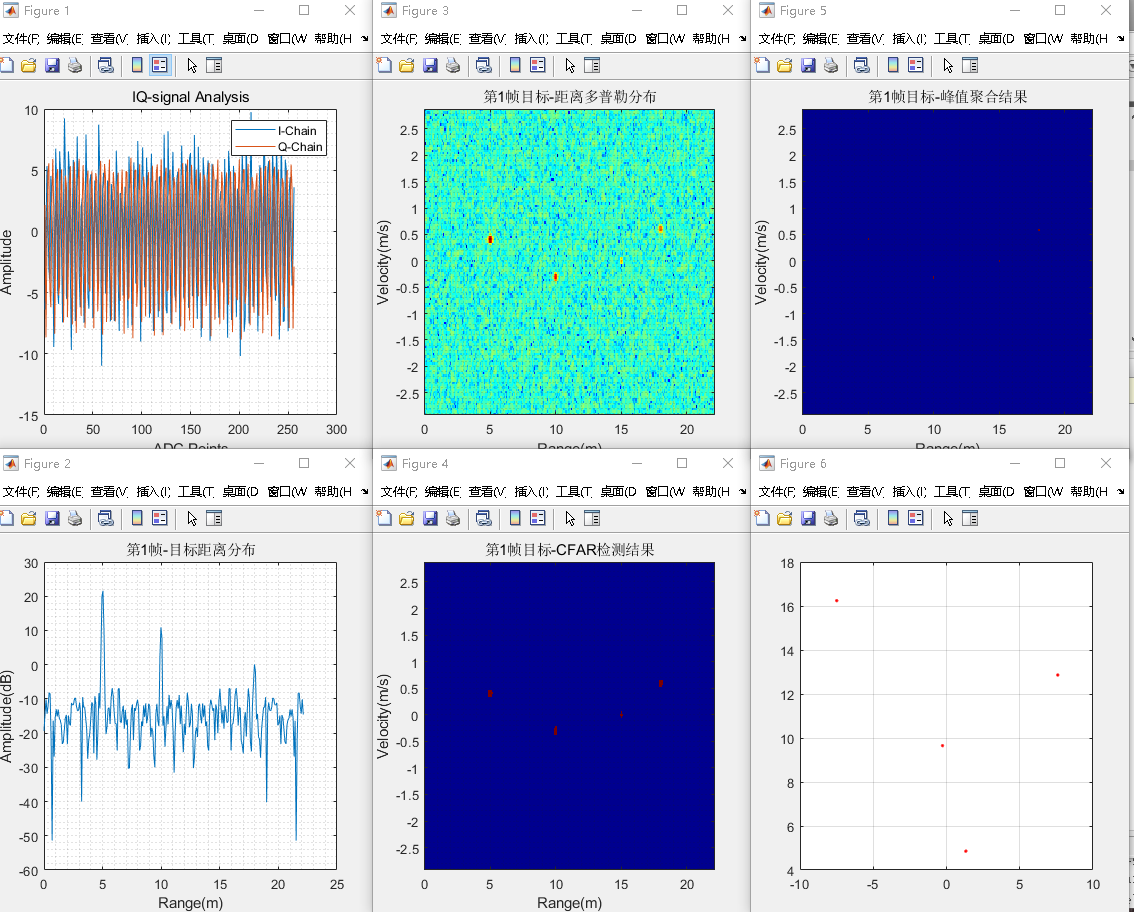
本完整程序可以通过邮箱形式向笔者咨询,希望读者以诚心求学心态咨询。
参考文献
[1] X. Yu, Z. Cao, Z. Wu, C. Song, J. Zhu and Z. Xu, "A Novel Potential Drowning Detection System Based on Millimeter-Wave Radar," 2022 17th International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, Singapore, 2022, pp. 659-664, doi: 10.1109/ICARCV57592.2022.10004245.
[2] J. Fuchs, M. Gardill, M. Lübke, A. Dubey and F. Lurz, "A Machine Learning Perspective on Automotive Radar Direction of Arrival Estimation," in IEEE Access, vol. 10, pp. 6775-6797, 2022, doi: 10.1109/ACCESS.2022.3141587.
[3] 初出茅庐:毫米波雷达开发手册之基础参数
https://www.cnblogs.com/yuxuliang/p/MyRadar_4.html