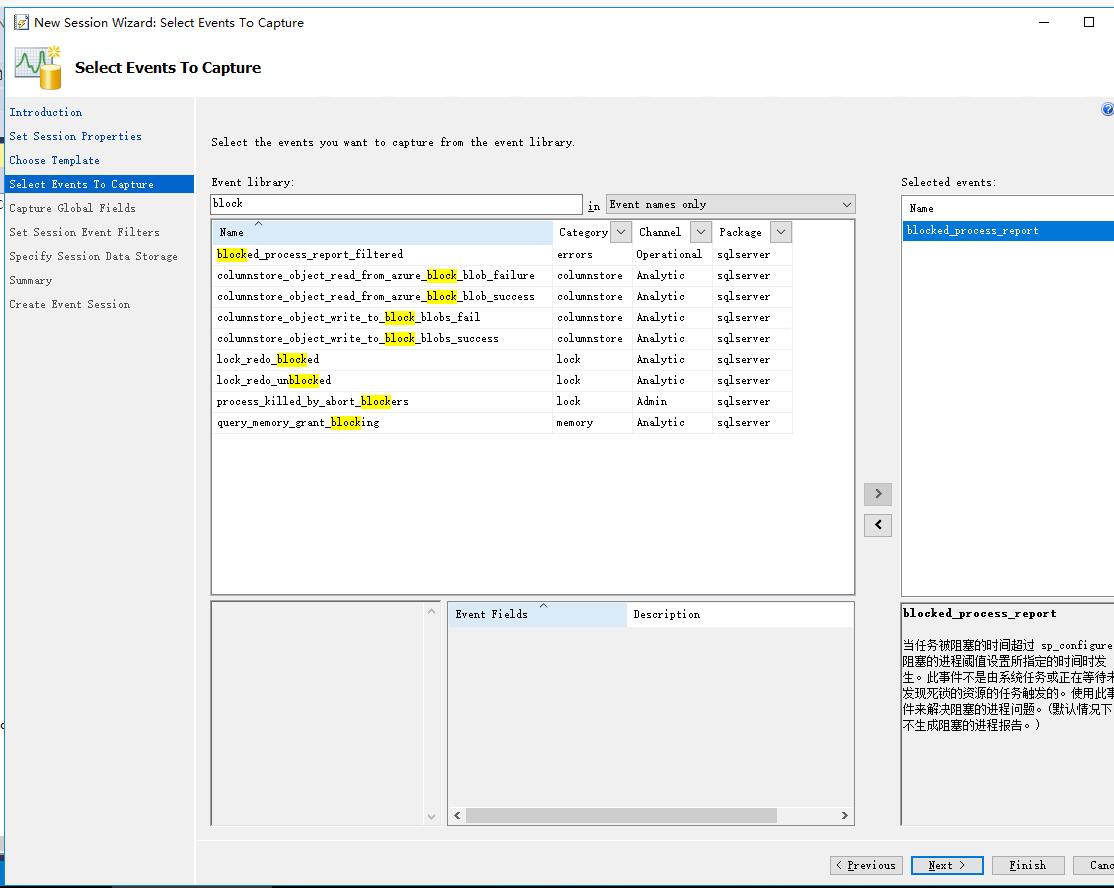
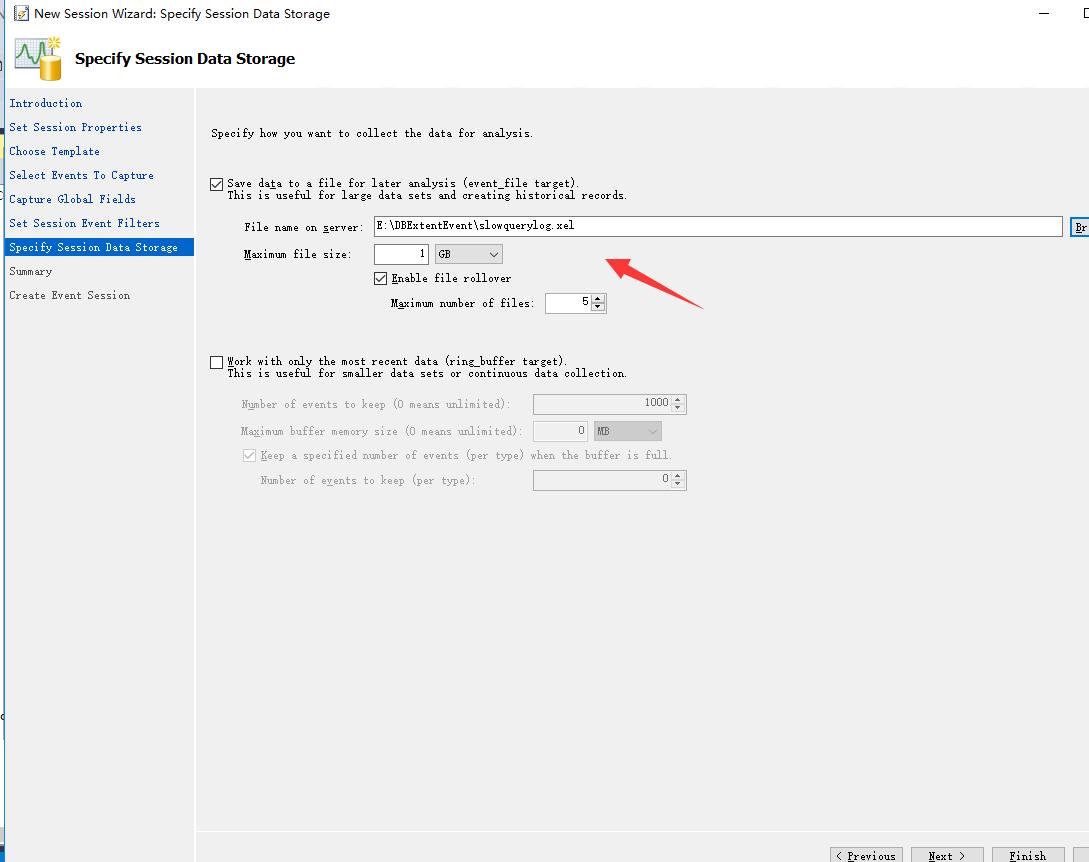
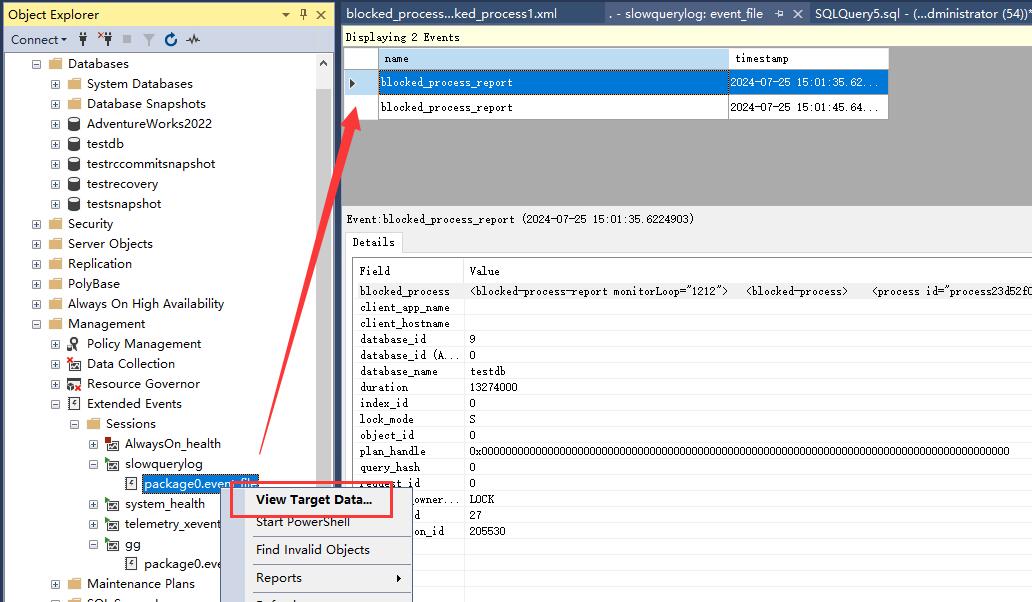
傅里叶级数和信号频谱
对于一个确定的时域信号,我们只需要知道它的函数表达式就可以在任意时刻确定一个信号,但是各种场景下中我们需要的往往并不是这样的解析式,因为这些复杂的式子首先难以快速准确地获得,另外难以进行快速进行分析,其中所蕴含的信息也难以提取。因此需要一种更高效的工具来进行信号的分析。
傅里叶级数的三角形式
傅里叶曾提出可以采用三角函数的线性组合表示一个时域上连续周期信号的想法。后面经过数学家对相关问题的研究得到如下结论:
当周期信号满足 $Dirichlet$ 条件,可以**唯一的**用三角函数线性组合来表示,如周期为 $T$ 频率为 $\displaystyle\omega = {2\pi\over T}$ 可以展开成如下式子:
$$
f(t) = a_0 + \sum_{n = 1}^{\infty}\big[a_n \cos{(n\omega t)} + b_n \sin{(n\omega t)}\big]
$$
其中
$$
\begin{aligned}
a_0 & = {1\over T} \int_{t_0}^{t_0+T} f(t) \text{d}t\\
a_n & = {2\over T} \int_{t_0}^{t_0+T} f(t) \cos{(n\omega t)}\text{d}t\\
b_n & = {2\over T} \int_{t_0}^{t_0+T} f(t) \sin{(n\omega t)}\text{d}t\\
\end{aligned}
$$
$Dirichlet$ 条件为:
1. 一个周期内间断点有限
2. 一个周期内信号绝对可积
3. 极大值和极小值的数目是有限的
对于常见的信号,
\(Dirichlet\)
条件都是满足的,可以不加验证的使用
如果使用三角公式将同频正余弦合并可以得到下面两种形式:
$$
\begin{aligned}
f(t) & = c_0 + \sum_{n = 0}^{\infty}c_n\cos{(n\omega t + \varphi_n)} \\
f(t) & = d_0 + \sum_{n = 0}^{\infty}d_n\sin{(n\omega t + \theta_n)} \\
\end{aligned}
$$
傅里叶级数不同表示形式下,量值之间的关系:
\[\large
\begin{cases}
& a_0 = b_0 = c_0\\
\\
& c_n = d_n = \sqrt{a_n^2 + b_n^2}\\
\\
& a_n = c_n\cos{\varphi_n} = d_n\sin{\theta_n}\\
\\
& b_n = -c_n\sin(\varphi_n) = d_n\cos{\theta_n}\\
\\
& \tan{\theta_n} = \displaystyle{a_n \over b_n}\\
\\
& \tan{\varphi_n} = \displaystyle-{b_n \over a_n}\\
\end{cases}
\]
利用上述的数学工具,我们很容易能够将一个连续的周期信号转变为三角函数,并且这个表达式中含有三个未知量————幅值、相位和频率,并且三者之间存在密切的关系。三个未知量,至少需要两个关系来描述,容易发现最方便构造数学关系的是幅值和频率以及相位与频率的关系,因为频率一般是个单调的函数,而另外两者则未必。于是分别得到幅度和频率的关系和相位和频率的关系,并分别将他们绘制出来就可以得到一组曲线————幅频曲线和相频曲线,分别称为幅度谱和相位谱。绘制过程中我们发现实际上信号包含的频率只在某些特定频率处取值,这就意味着我们绘制出来的图像是个离散图像,幅度谱和相位谱在这个频率上都为一个有限值,绘制出来只有一根根线,因此称为谱线,将每一根谱线顶端连起来,我们就可以看到谱线的大致走势。
傅里叶级数的复指数形式
上述表达式是一个三角函数表达式,当我们需要求解某一个具体周期信号的时候需要分别求出
\(a_0\)
、
\(a_n\)
和
\(b_n\)
,这个过程是繁琐的。
能否找到一个统一的表达式,使得能够同时求出这三者?
答案是利用欧拉公式
\[e^{j\theta} = \cos(\theta) + j \sin(\theta)
\]
欧拉公式可以在复数域上把三角函数表示为指数函数。
因此我们可以将上面的表达式转换成复指数的形式,具体过程如下:
\[\begin{aligned}
f(t) = &a_{0}+ \sum_{n = 1}^{\infty} \left( a_{n} \frac{e^{jn\omega t} + e^{-jn\omega t}}{2} + b_{n} \frac{e^{jn\omega t} - e^{-jn\omega t}}{2j}\right)\\
=&a_0 + \sum_{n = 1}^{\infty} ({a_n - jb_n \over 2}e^{jn\omega t} + {a_n + j b_n \over 2}e^{-jn\omega t})\\
\end{aligned}
\]
接下来,我们回过去看
\(a_n\)
与
\(b_n\)
的原始定义(积分表达式),如果
\(n\)
是一个整数,而不像前文那样定义为自然数, 则容易得到
\(a_n\)
是偶函数,
\(b_n\)
是奇函数。
于是我们不妨定义函数
\[F(n\omega) = {a_n - jb_n \over 2}
\]
结合上面的奇偶性分析有
\[\begin{aligned}
F(-n\omega) & = {a_{-n} - jb_{-n}\over 2} \\
& = {a_{n} + jb_{n}\over 2}
\end{aligned}
\]
我们发现
\(F(n\omega)\)
与
\(F(-n\omega)\)
是共轭的,恰好为复数表示的傅里叶级数的同一频次的两项。如果我们定义
\(F(0) = a_0\)
,我们便可以将傅里叶级数的复数形式写成下面这样:
\[f(t) = \sum_{n = -\infty}^{\infty} (F(n\omega)e^{jn\omega t})
\]
其中:
\[F_n(n\omega) = {1\over T} \int_{t_0}^{t_0 + T} f(t) e^{-jn\omega t}\text{d}t \\
\]
这样我们求解傅里叶级数将更加方便,不像三角形式那样需要求解好几个式子,但是
代价就是需要进行复变函数的积分,可能较为繁琐
。
傅里叶指数形式与傅里叶级数中相关参数的关系:
\[\large
\begin{cases}
& F_0 = c_0 = d_0 = a_0\\
\\
& F_n = |F_n|e^{j\varphi_n} = \displaystyle{a_n - jb_n \over 2} \\
\\
& F_{-n} = |F_{-n}|e^{-j\varphi_n} = \displaystyle{a_n + jb_n \over 2} \\
\\
& |F_n| = |F_{-n}| = \displaystyle{1\over 2}c_n = \displaystyle{1\over2}d_n = {1\over2}\displaystyle\sqrt{a_n^2 + b_n^2}\\
\\
& |F_n| + |F_{-n}| = c_n \\
\\
& a_n = F_n + F_{-n} \\
\\
& b_n = j( F_n + F_{-n} ) \\
\\
& c_n^2 = d_n^2 = a_n^2 + b_n^2 = 4F_n F_{-n}
\end{cases}
\]
由于
\(F(n\omega)\)
与
\(F(-n\omega)\)
是共轭的,所以复指数形式的谱图中幅度谱是左右对称的偶函数,相位谱是奇函数,并且一般位于二四象限。
值得注意的是在幅度谱中复指数的谱图中与傅里叶级数谱图对应位置相比,前者高度为后者的
一半
,也就是正频率项和复频率项相加即为实数形式的谱图。
注意复频率的出现主要是数学上的结果,并不具备实际意义。
傅里叶级数与函数对称性的关系
周期函数的对称性主要分为两类:
- 对整周期对称,如奇函数和偶函数。
- 对半周期对称,奇谐函数。
偶函数
定义:
\[f(t) = f(-t)\\
\]
图像上:关于坐标轴对称
对于偶函数存在下列结论:
\[\large
\begin{cases}
a_{n}= \frac{4}{T}\displaystyle\int_{0}^{\frac{T}{2}}f(t)\cos{ (n\omega t )}\text{d}t \\ \\
b_{n} = 0 \\ \\
c_{n} = d_{n} = a_{n} = 2 F_{n} \\ \\
F_{n} = F_{-n} = \displaystyle\frac{a_{n}}{2} \\ \\
\varphi_{n} = 0 \\ \\
\theta_{n} = \displaystyle\frac{\pi}{2} \\ \\
\end{cases}
\]
结论:偶函数的傅里叶级数展开中仅包含余弦项,不包含正弦项。并且复指数形式为实函数。
奇函数
定义:
\[f(t) = -f(-t)
\]
图像上:关于原点对称
奇函数相关的结论 :
\[\large
\begin{cases}
a_{0} = 0,a_{n} = 0 \\ \\
b_{n} = \frac{4}{T} \displaystyle \int_{0}^{\frac {T}{2}} f(t)\sin(n\omega t) \text{d}t\\ \\
c_{n} = d_{n} = b_{n} = 2 j F_{n}\\ \\
F_{n} = -F_{-n} = - \frac{1}{2} j b_{n}\\ \\
\varphi_{n} = -\frac{\pi}{2}\\ \\
\theta_{n} = 0\\ \\
\end{cases}
\]
结论:奇函数的
\(F_{n}\)
为虚函数。奇函数的傅里叶级数中不存在余弦项,只存在正弦项。若是奇函数再加上一个直流分量,则除了
\(a_{0}\)
不为
\(0\)
,其他结论不存在任何变化。
(三)奇谐函数
定义:
\[f(t) = -f\left( t \pm \frac{T}{2} \right)
\]
图像上:平移半周期再沿着x轴翻转后与原函数重合
奇谐函数相关结论:
\[\begin{cases}
a_{0} = 0 \\ \\
a_{n} = b_{n} = 0 \qquad (n \text{为偶数}) \\ \\
a_{n} = \displaystyle \frac{4}{T} \displaystyle \int_{0}^{\frac{T}{2}} f(t) \sin(n \omega t ) \text{d} t \qquad (n \text{为奇数})\\ \\
a_{n} = \displaystyle \frac{4}{T} \displaystyle \int_{0}^{\frac{T}{2}} f(t) \cos(n \omega t ) \text{d} t \qquad (n \text{为奇数})\\ \\
\end{cases}
\]
结论:
奇谐函数不存在偶数频次的谐波,仅存在奇次谐波的正弦和余弦项。
或许你在思考为什么上面的分类中半周期对称性仅仅说了奇谐函数,为什么没有说偶谐函数呢?
这个问题问得好,因为仿照奇谐函数的定义写出偶谐函数,我们可以发现偶谐函数就是周期是原函数一半的周期函数,原函数确定的情况下傅里叶级数是唯一的,因此我们把它放在讨论中的第一类,也就是整周期对称性。
帕塞瓦尔定理
帕塞瓦尔定理是个广泛存在于信号分析各种变换之间的定理,一般结论是,能量信号(能量是个有限值)在时域上的能量和频域上的能量是相等的,功率信号(功率是个有限值)在时域上的功率和频域上的功率是相等的。
对于这里的连续周期信号,往往能量不是有限的,功率是个有限值,也就是是功率信号,它的功率等于傅里叶级数展开后各分量有效值的平方和。
典型周期信号的傅里叶变换
(一)周期矩形脉冲信号
设周期矩形脉冲信号
\(f(t)\)
的脉冲宽度为
\(t\)
周期为
\(T\)
,脉冲幅度为
\(E\)
,则他的傅里叶级数展开形式如下:
\[\large
\begin{cases}
a_{0} = \frac{{E\tau}}{T}\\ \\
a_{n} = \frac{{2 E \tau}}{T} \text{Sa}\left( \frac{{n \pi \tau}}{T} \right) = \frac{{E \tau \omega}}{\pi} \text{Sa}\left( \frac{{n\omega\tau}}{2} \right)\\ \\
b_{n} = 0\\ \\
F_{n} = \frac{{E \tau}}{T} \text{Sa} \left( \frac{{n\omega \tau}}{2} \right)\\ \\
c_{n} = a_{n}\\ \\
c_{0} = a_{0} \\
\end{cases}
\]
结论:
- 周期矩形脉冲的频谱是离散的,重复周期周期越大,谱线越靠近。
- 直流分量,和各频次分量的大小与脉幅和脉宽成正比,与重复周期成反比
- 周期信号包含无穷多谱线,其中能量主要集中在第一次过零点内,也就是
\(\omega < \displaystyle{\frac{{2\pi}}{\tau}}\)
内
我们称这样的区域为频带,频带宽度为
\(B_{\omega} = \displaystyle\frac{{2\pi}}{\tau}\)
或者
\(B_{f } = \displaystyle\frac{1}{\tau}\)
,频带宽度只与脉宽有关,并且成反比。
对称方波信号也是矩形信号的一种特殊情况:
- 它是正负交替的信号,其直流分量
\(a_{0}\)
等于零
- 他的脉宽恰好等于周期的一半,即
\(\tau = \displaystyle\frac{T}{2}\)
对称方波的傅里叶级数形式为:
\[\begin{aligned}
f(t) & = \frac{{2E}}{\pi} \sum_{n = 1}^{\infty} \frac{1}{n} \sin\left( \frac{{n\pi}}{2} \right) \cos({n \omega t})\\
& = \frac{{2E}}{\pi} \left[ \cos({\omega t}) + \frac{1}{3} \cos(3\omega t +\pi) + \frac{1}{5} \cos({5\omega t}) + \cdots \right]
\end{aligned}
\]
对称方波的谐波幅度以
\(\displaystyle\frac{1}{n}\)
收敛。
(二)周期锯齿脉冲信号
峰值和谷值分别为
\(\displaystyle \pm\frac{E}{2}\)
,周期为
\(T\)
,信号是奇函数,因此傅里叶级数仅存在正弦分量。 谐波幅度以
\(\displaystyle\frac{1}{n}\)
的规律收敛。
\[f(t) = \frac{E}{\pi} \sum_{n=1}^{\infty} (-1)^{n+1} \frac{1}{n} \sin({n \omega t}).
\]
(三)周期三角脉冲信号
峰值为
\(E\)
谷值为
\(0\)
,周期为
\(T\)
,是偶函数,仅存在余弦分量。
\[\begin{aligned}
f(t) & = \frac{E}{2} + \frac{4E}{\pi^{2}} \left[ \cos(\omega t) + \frac{1}{3^{2}}\cos({3\omega t}) + \frac{1}{5^{2}} \cos({5 \omega t}) +\cdots \right]\\ \\
& = \frac{E}{2} + \frac{4E}{\pi^{2}}\sum_{n=1}^{\infty} \frac{1}{n^{2}} \sin^{2}\left( {\frac{n\pi}{2}} \right) \cos({n \omega t}) \\
\end{aligned}
\]
(四)周期半波余弦信号
偶函数,仅存在直流、基波和偶次谐波频率分量,谐波的幅度以
\(\displaystyle \frac{1}{n^{2}}\)
规律收敛。
\[\begin{aligned}
f(t) & = \frac{E}{2} + \frac{E}{2} \left[ \cos({\omega t}) + \frac{4}{3\pi} \cos({2 \omega t}) - \frac{4}{15\pi} \cos({4 \omega t}) +\cdots \right] \\ \\
& = \frac{E}{\pi} - \frac{2E}{\pi} \sum_{n=1}^{\infty} \frac{1}{(n^{2}-1)} \cos\left( \frac{{n\pi}}{2} \right) \cos(n \omega t).\\
\end{aligned}
\]
(五)周期全波余弦信号
周期全波余弦只包含直流分量和偶次谐波分量,谐波的幅度以
\(\displaystyle{\frac{1}{n^{2}}}\)
规律收敛 。
\[\begin{aligned}
f(t) & = \frac{2e}{\pi} + \frac{4E}{\pi} \left[ \frac{1}{3}\cos({2 \omega t}) - \frac{1}{15}\cos({4 \omega t}) + \frac{1}{35} \cos({6 \omega t}) \right]\\ \\
& = \frac{2E}{\pi} + \frac{4E}{\pi} \sum_{n=1}^{\infty} (-1)^{n+1} \frac{1}{(4n^{2} -1 )} \cos(2n \omega t)\\
\end{aligned}
\]
对于上述周期函数,周期矩形脉冲信号是最重要的一个
,需要进行仔细研究。
傅里叶级数举例和有限项逼近是带来的误差
实际工程中,我们无法做到将傅里叶级数展开到无穷项,我们只能展开到有限项。有限项算出的结果与真实值之间到底存在多少的误差是我们关心的。
误差即为后面无穷项之和:
\[\epsilon_{N}(t) = \sum_{n = N}^{\infty}[ a_{n} \cos(n\omega t) + b_{n} \sin(n \omega t)]
\]
方均误差为:
\[\begin{aligned}
E_{N} = \overline{ \epsilon_{n}^2(t) } & = \frac{1}{T} \int_{t_{0}}^{t_{0} + T} \epsilon_{N}(t)^2 \text{d}t \\
& = \overline{f^2(t)} - \bigg[a_{0}^2 + \frac{1}{2} \sum_{n=1}^{N}(a_{n}^2 + b_{n}^2) \bigg]\\
\end{aligned}
\]
下面,我们选择周期为2,幅值为1的周期矩形脉冲信号。
|
成分
|
图像
|
| 展开至基波 |
 |
| 展开至3次谐波 |
 |
| 展开至5次谐波 |
 |
| 展开至7次谐波 |
 |
| 展开至9次谐波 |
 |
| 展开至11次谐波 |
 |
通过观察上面的一组图像,我们可以发现如下规律:
- 傅里叶级数取的次数越多,最后的波形越接近原信号
- 高频信号主要影响的是信号中变化快速的部分;如信号为脉冲信号时,高频信号主要影响的是脉冲的跳变沿
- 低频信号主要影响的是信号中缓慢变化的部分;如信号为脉冲信号时,低频信号主要影响的时脉冲的顶部
- 当信号中任意频谱分量的幅值或者相位发生变化时,输出波形一般会失真,如在图像处理的时候,我们发现两张图片频谱的幅度不变,相位谱图互换后叠加,图像本身基本未发生改变,但是细节上稍微有些不同。
另外我们注意到一个有趣但又让人苦恼的地方。周期矩形脉冲信号的跳变边沿处有一个小的峰起,并且无论取多少项,这个峰起并没有因取的傅里叶级数项数变多而明显减小。
关于这样一个问题,信号分析中称其为
\(Gibbs\)
现象
。具体内容为:
在进行有限项傅里叶级数逼近时,随着采用更多的傅里叶级数成分或分量,傅里叶级数在接近(完整)跳跃的约
\(9%\)
的跳跃点附近显示出振荡行为中的第一个超调,并且该振荡不会消失,而是越来越接近该点,使得振荡积分接近零(即振荡能量为零)
。