从DDPM到DDIM
从DDPM到DDIM (一)
现在网络上关于DDPM和DDIM的讲解有很多,但无论什么样的讲解,都不如自己推到一边来的痛快。笔者希望就这篇文章,从头到尾对扩散模型做一次完整的推导。
DDPM是一个双向马尔可夫模型,其分为扩散过程和采样过程。
扩散过程是对于图片不断加噪的过程,每一步添加少量的高斯噪声,直到图像完全变为纯高斯噪声。
为什么逐步添加小的高斯噪声,而不是一步到位,直接添加很强的噪声呢?这一点我们留到之后来探讨。
采样过程则相反,是对纯高斯噪声图像不断去噪,逐步恢复原始图像的过程。
下图展示了DDPM原文中的马尔可夫模型。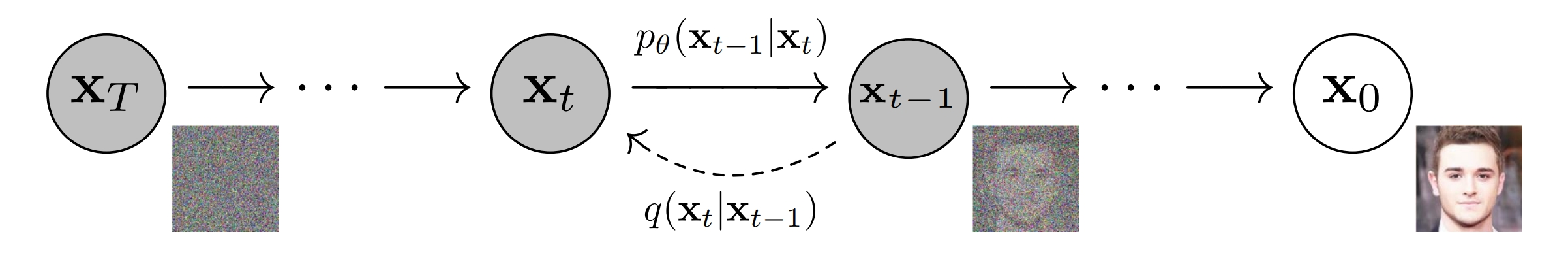
其中
\(\mathbf{x}_T\)
代表纯高斯噪声,
\(\mathbf{x}_t, 0 < t < T\)
代表中间的隐变量,
\(\mathbf{x}_0\)
代表生成的图像。从
\(\mathbf{x}_0\)
逐步加噪到
\(\mathbf{x}_T\)
的过程是不需要神经网络参数的,简单地讲高斯噪声和图像或者隐变量进行线性组合即可,单步加噪过程用
\(q(\mathbf{x}_t | \mathbf{x}_{t-1})\)
来表示。但是去噪的过程,我们是不知道的,这里的单步去噪过程,我们用
\(p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_{t})\)
来表示。之所以这里增加一个
\(\theta\)
下标,是因为
\(p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_{t})\)
是用神经网络来逼近的转移概率,
\(\theta\)
代表神经网络参数。
扩散模型首先需要大量的图片进行训练,训练的目标就是估计图像的概率分布。训练完毕后,生成图像的过程就是在计算出的概率分布中采样。因此生成模型一般都有训练算法和采样算法,VAE、GAN、diffusion,还有如今大火的大预言模型(LLM)都不例外。本文讨论的DDPM和DDIM在训练方法上是一样的,只是DDIM在采样方法上与前者有所不同。
而训练算法的最经典的方法就是极大似然估计,我们从极大似然估计开始。
1、从极大似然估计开始
首先简单回顾一下概率论中的概率论中的一些基本概念。
1.1、概念回顾
边缘概率密度和联合概率密度
: 大家可能还记得概率论中的边缘概率密度,忘了也不要紧,我们简单回顾一下。对于二维随机变量
\((X, Y)\)
,其联合概率密度函数是
\(f(x, y)\)
,那么我不管
\(Y\)
,单看
\(X\)
的概率密度,就是
\(X\)
的边缘概率密度,其计算方式如下:
f_{X}(t) = \int_{-\infty}^{\infty} f(x, y) d y \\
\end{aligned} \\
\]
概率乘法公式
: 对于联合概率
\(P(A_1 A_2 ... A_{n})\)
,若
\(P(A_1 A_2 ... A_{n-1}) 0\)
,则:
P(A_1 A_2 ... A_{n}) &= P(A_1 A_2 ... A_{n-1}) P(A_n | A_1 A_2 ... A_{n-1}) \\
&= P(A_1) P(A_2 | A_1) P(A_3 | A_1 A_2) ... P(A_n | A_1 A_2 ... A_{n-1})
\end{aligned} \\
\]
概率乘法公式可以用条件概率的定义和数学归纳法证明。
马尔可夫链定义
: 随机过程
\(\left\{X_n, n = 0,1,2,...\right\}\)
称为
马尔可夫链
,若随机过程在某一时刻的随机变量
\(X_n\)
只取有限或可列个值(比如非负整数集,若不另外说明,以集合
\(\mathcal{S}\)
来表示),并且对于任意的
\(n \geq 0\)
,及任意状态
\(i, j, i_0, i_1, ..., i_{n-1} \in \mathcal{S}\)
,有
P(X_{n+1} = j | X_{0} = i_{0}, X_{1} = i_{1}, ... X_{n} = i) = P(X_{n+1} = j | X_{n} = i) \\
\end{aligned} \\
\]
其中
\(X_n = i\)
表示过程在时刻
\(n\)
处于状态
\(i\)
。称
\(\mathcal{S}\)
为该过程的状态空间。上式刻画了马尔可夫链的特性,称为马尔可夫性。
1.2、概率分布表示
生成模型的主要目标是估计需要生成的数据的概率分布。这里就是
\(p\left(\mathbf{x}_0\right)\)
,如何估计
\(p\left(\mathbf{x}_0\right)\)
呢。一个比较直接的想法就是把
\(p\left(\mathbf{x}_0\right)\)
当作整个马尔可夫模型的边缘概率:
p\left(\mathbf{x}_0\right) = \int p\left(\mathbf{x}_{0:T}\right) d \mathbf{x}_{1:T} \\
\end{aligned} \\
\]
这里
\(p\left(\mathbf{x}_{0:T}\right)\)
表示
\(\mathbf{x}_{0}, \mathbf{x}_{1}, ..., \mathbf{x}_{T}\)
多个随机变量的联合概率分布。
\(d \mathbf{x}_{1:T}\)
表示对
\(\mathbf{x}_{1}, \mathbf{x}_{2}, ..., \mathbf{x}_{T}\)
这
\(T\)
个随机变量求多重积分。
显然,这个积分很不好求。Sohl-Dickstein等人在2015年的扩散模型的开山之作
[1]
中,采用的是这个方法:
p\left(\mathbf{x}_0\right) &= \int p\left(\mathbf{x}_{0:T}\right) \textcolor{blue}{\frac{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)}} d \mathbf{x}_{1:T} \quad\quad 积分内部乘1\\
&= \int \textcolor{blue}{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)} \frac{p\left(\mathbf{x}_{0:T}\right)}{\textcolor{blue}{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)}} d \mathbf{x}_{1:T} \\
&= \mathbb{E}_{\textcolor{blue}{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)}} \left[\frac{p\left(\mathbf{x}_{0:T}\right)}{\textcolor{blue}{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)}}\right] \quad\quad随机变量函数的期望\\
\end{aligned} \tag{1}
\]
Sohl-Dickstein等人借鉴的是统计物理中的技巧:退火重要性采样(annealed importance sampling) 和 Jarzynski equality。这两个就涉及到笔者的知识盲区了,感兴趣的同学可以自行找相关资料学习。(果然数学物理基础不牢就搞不好科研~)。
这里有的同学可能会有疑问,为什么用分子分母都为
\(q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)\)
的因子乘进去?这里笔者尝试给出另一种解释,就是我们在求边缘分布的时候,可以尝试将联合概率分布拆开,然后想办法乘一个已知的并且与其类似的项,然后将这些项分别放在分子与分母的位置,让他们分别进行比较。因为这是KL散度的形式,而KL散度是比较好算的。
\(q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)\)
的好处就是也可以按照贝叶斯公式和马尔可夫性质拆解成多个条件概率的连乘积,这些条件概率与
\(p\left(\mathbf{x}_{0:T}\right)\)
拆解之后的条件概率几乎可以一一对应,而且每个条件概率表示的都是扩散过程的单步转移概率,这我们都是知道的。那么为什么不用
\(q\left(\mathbf{x}_{0:T}\right)\)
呢?其实
\(p\)
和
\(q\)
本质上是一种符号,
\(q\left(\mathbf{x}_{0:T}\right)\)
和
\(p\left(\mathbf{x}_{0:T}\right)\)
其实表示的是一个东西。
这里自然就引出了问题,这么一堆随机变量的联合概率密度,我们还是不知道啊,
\(p\left(\mathbf{x}_{0:T}\right)\)
和
\(q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)\)
如何该表示?
利用概率乘法公式,有:
p\left(\mathbf{x}_{0:T}\right) &= p\left(\mathbf{x}_{T}\right) p\left(\mathbf{x}_{T-1}|\mathbf{x}_{T}\right) p\left(\mathbf{x}_{T-2}|\mathbf{x}_{T-1},\mathbf{x}_{T}\right) ... p\left(\mathbf{x}_{0}|\mathbf{x}_{1:T}\right)\\
\end{aligned} \tag{2}
\]
我们这里是单独把
\(p\left(\mathbf{x}_{T}\right)\)
,单独提出来,这是因为
\(\mathbf{x}_{T}\)
服从高斯分布,这是我们知道的分布;如果反方向的来表示,这么表示的话:
p\left(\mathbf{x}_{0:T}\right) &= p\left(\mathbf{x}_{0}\right) p\left(\mathbf{x}_{1}|\mathbf{x}_{0}\right) p\left(\mathbf{x}_{2}|\mathbf{x}_{1},\mathbf{x}_{0}\right) ... p\left(\mathbf{x}_{T}|\mathbf{x}_{0:T-1}\right)\\
\end{aligned} \tag{3}
\]
(3)式这样表示明显不如(2)式,因为我们最初就是要求
\(p\left(\mathbf{x}_{0}\right)\)
,而计算(3)式则需要知道
\(p\left(\mathbf{x}_{0}\right)\)
,这样就陷入了死循环。因此学术界采用(2)式来对联合概率进行拆解。
因为扩散模型是马尔可夫链,某一时刻的随机变量只和前一个时刻有关,所以:
p\left(\mathbf{x}_{t-1}|\mathbf{x}_{\leq t}\right) = p\left(\mathbf{x}_{t-1}|\mathbf{x}_{t}\right)\\
\end{aligned} \\
\]
于是有:
p\left(\mathbf{x}_{0:T}\right) = p\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p\left(\mathbf{x}_{t-1}|\mathbf{x}_{t}\right)\\
\end{aligned} \\
\]
文章一开始说到,在扩散模型的采样过程中,单步转移概率是不知道的,需要用神经网络来拟合,所以我们给采样过程的单步转移概率都加一个下标
\(\theta\)
,这样就得到了最终的联合概率:
\textcolor{blue}{p\left(\mathbf{x}_{0:T}\right) = p\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p_{\theta}\left(\mathbf{x}_{t-1}|\mathbf{x}_{t}\right)}
\end{aligned} \tag{4}
\]
类似地,我们来计算
\(q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)\)
的拆解表示:
q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right) &= q\left(\mathbf{x}_{1} | \mathbf{x}_{0}\right) q\left(\mathbf{x}_{2} | \mathbf{x}_{0:1}\right) ... q\left(\mathbf{x}_{T} | \mathbf{x}_{0:T-1}\right) \quad\quad 概率乘法公式\\
&= \prod_{t=1}^T q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right) \quad\quad 马尔可夫性质\\
\end{aligned} \\
\]
于是得到了以
\(\mathbf{x}_0\)
为条件的扩散过程的联合概率分布:
\textcolor{blue}{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right) = \prod_{t=1}^T q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)} \\
\end{aligned} \tag{5}
\]
Sohl-Dickstein J, Weiss E, Maheswaranathan N, et al. Deep unsupervised learning using nonequilibrium thermodynamics[C]//International conference on machine learning. PMLR, 2015: 2256-2265.
↩︎