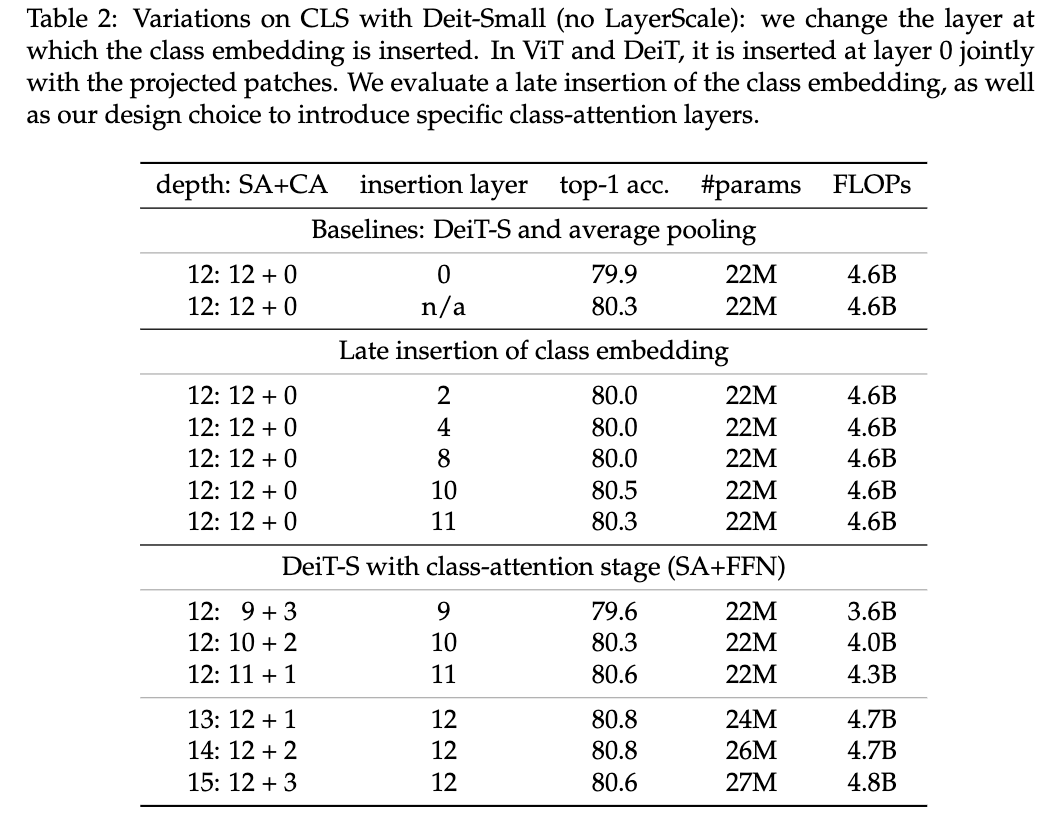
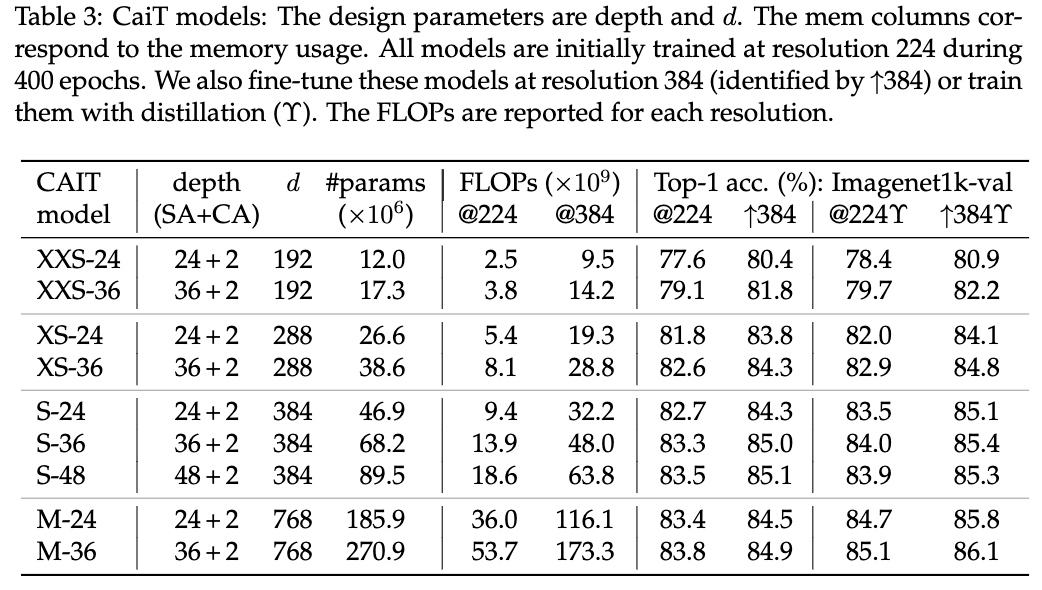
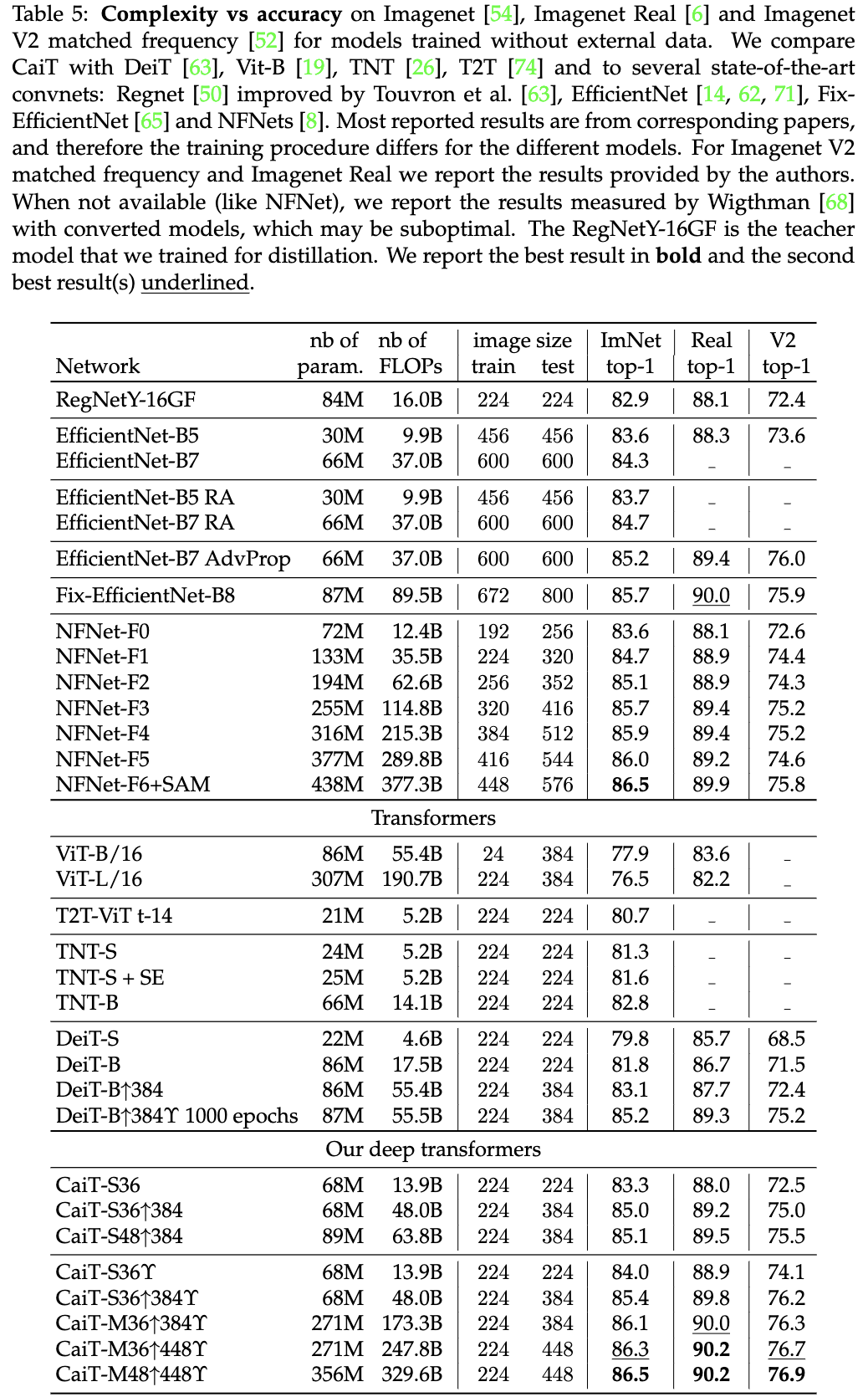
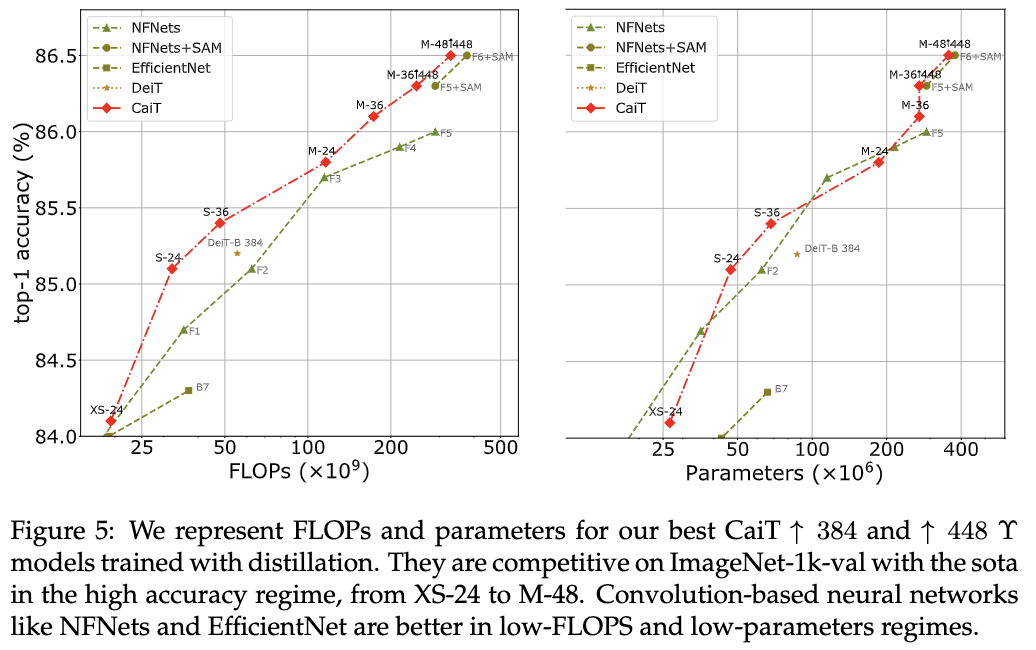
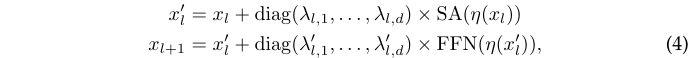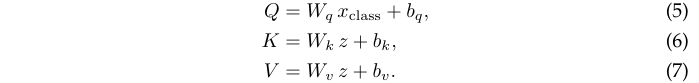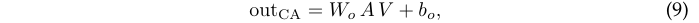归约证明在密码学中的应用
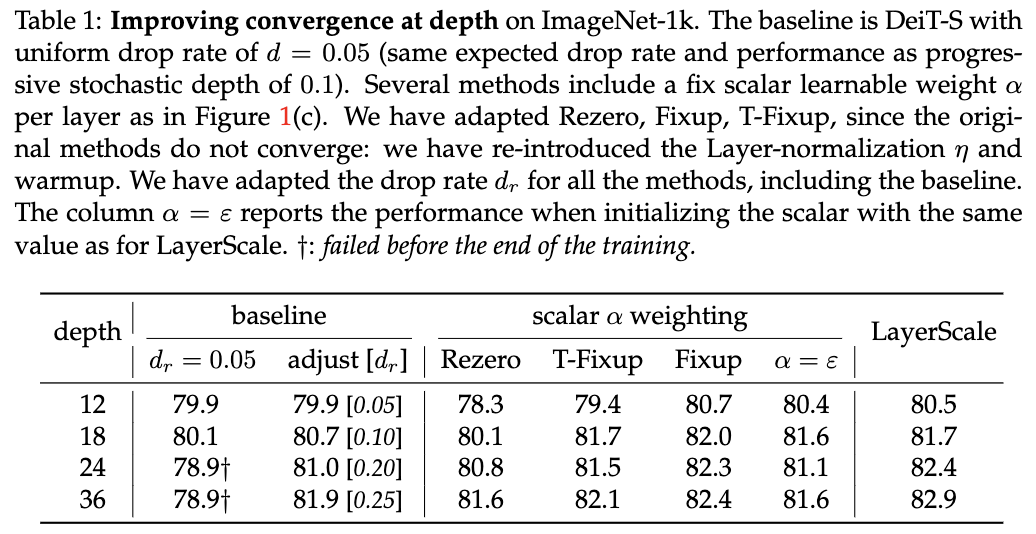
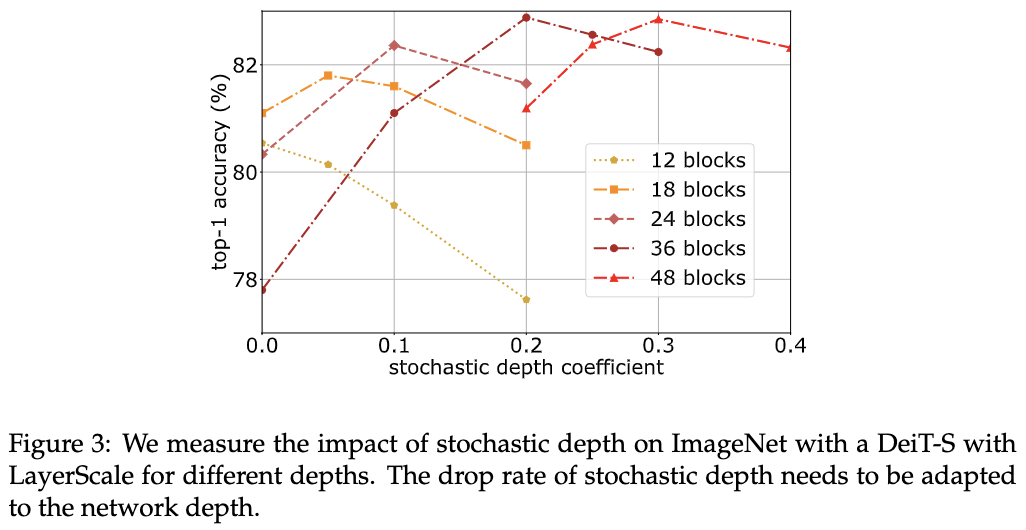
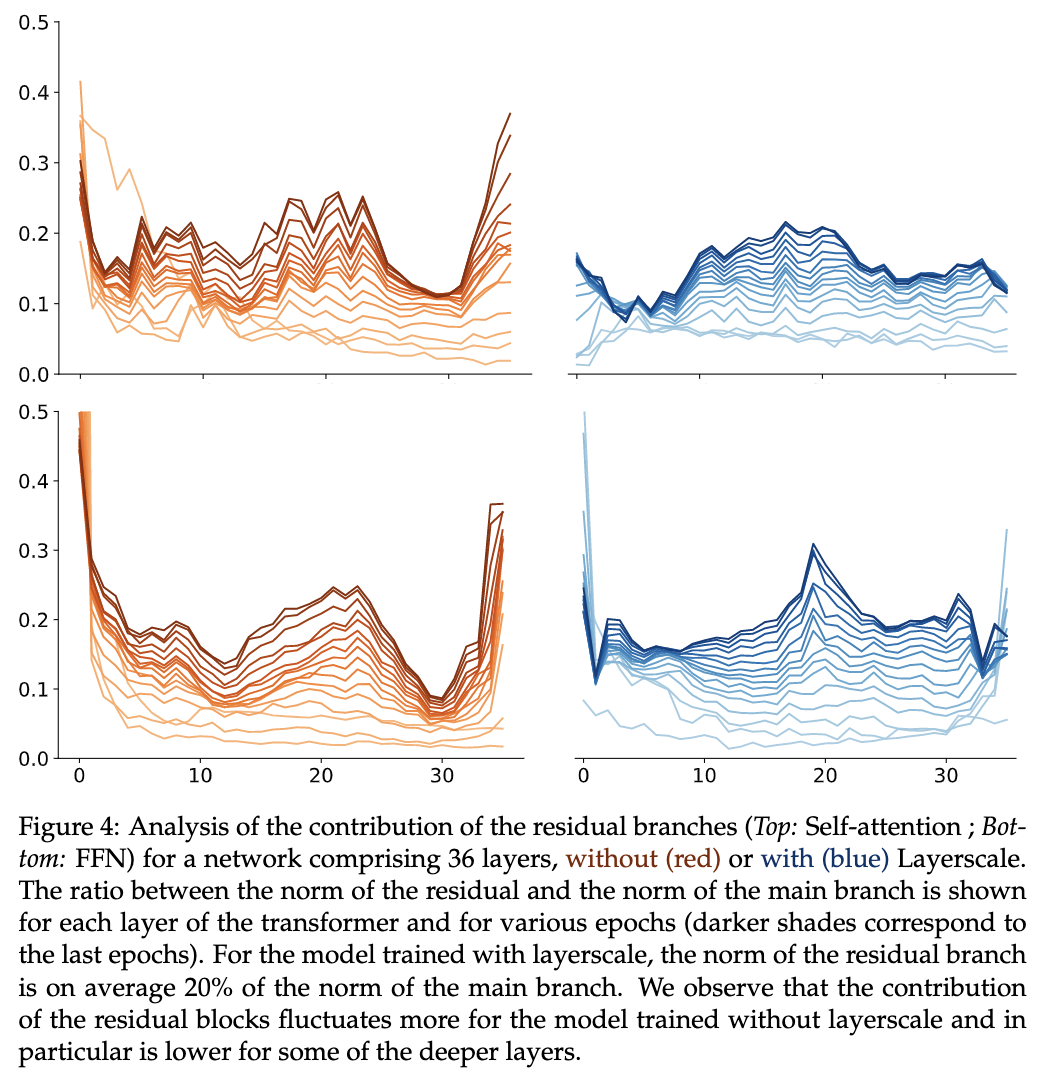
PrimiHub
一款由密码学专家团队打造的开源隐私计算平台,专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。
在现代信息社会,密码学在保护信息安全中扮演着至关重要的角色。而归约证明(Reduction Proof)作为密码学中的一个重要工具,通过将一个问题的安全性归约为另一个已知问题的难解性,从而证明新问题的安全性。本文将详细介绍归约证明的概念、步骤及其在密码学中的应用,并通过具体实例和图示来帮助读者更好地理解这一重要技术。
归约证明的基本概念
归约证明的定义
归约证明是一种证明方法,通过将一个待证明的问题(目标问题)转换为另一个已知难解的问题(基准问题),来证明目标问题的难度不低于基准问题。简单来说,假设我们已经知道某个问题很难解决,如果能证明我们要研究的问题至少和这个已知的难题一样难解,那么就可以认为我们的问题也具有相应的安全性。
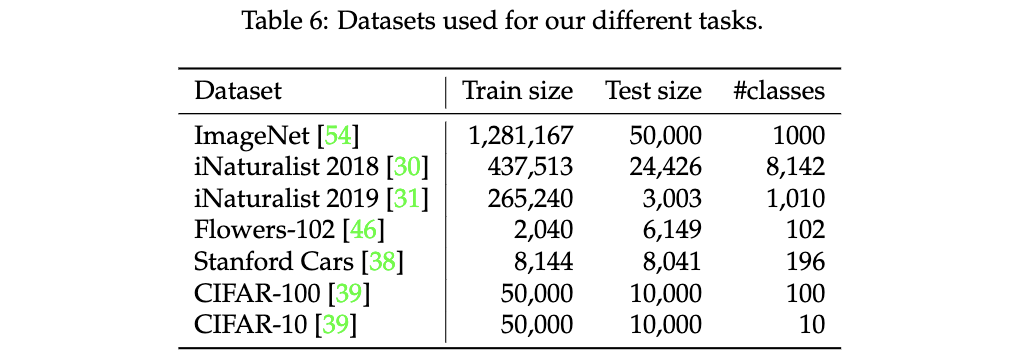
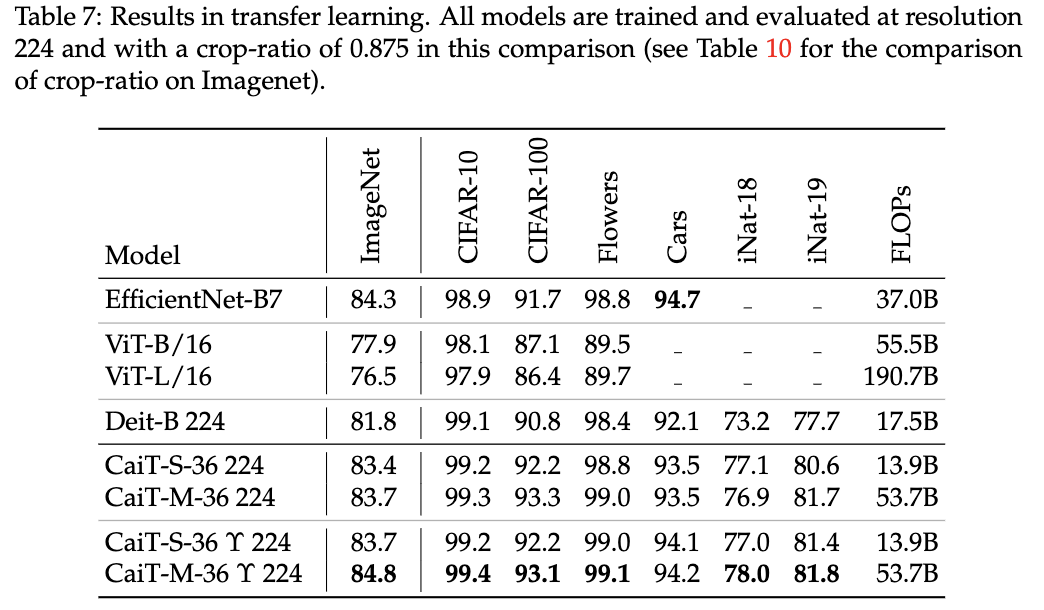
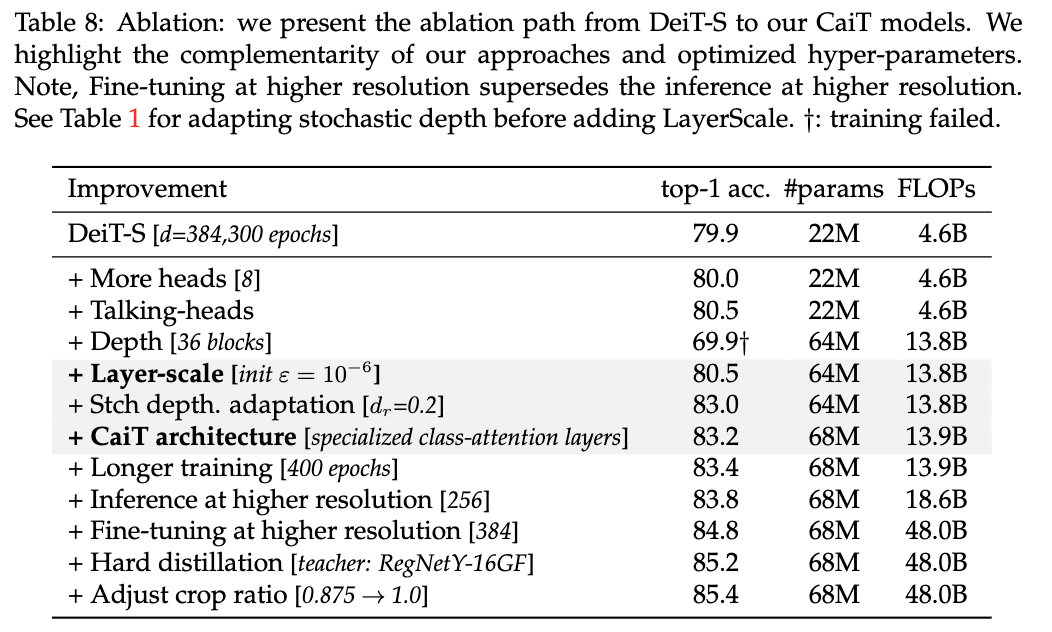
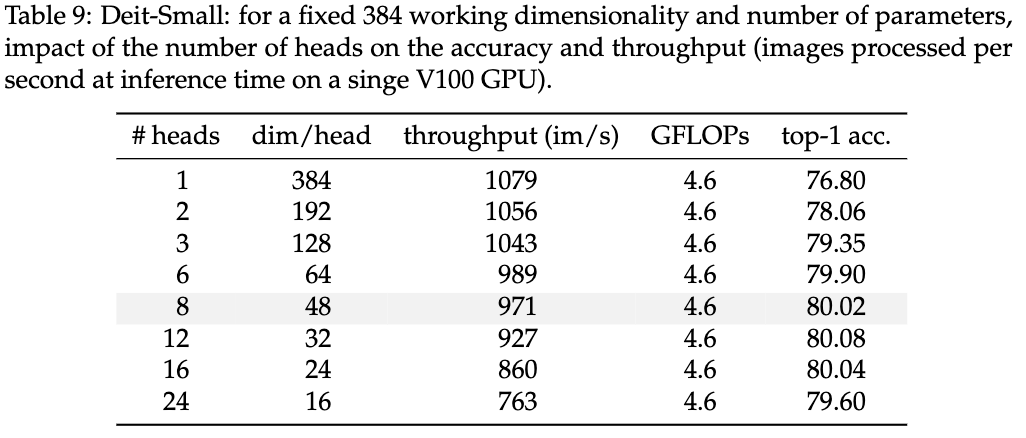
举例说明
设想我们有一个新的密码算法A,希望证明其安全性。已知离散对数问题(Discrete Logarithm Problem, DLP)是一个公认的难解问题。我们可以尝试通过归约证明:如果能够在多项式时间内破解算法A,那么也能在多项式时间内解决DLP。这就意味着破解算法A也是难解的,从而证明了算法A的安全性。
归约证明的步骤
归约证明一般包括以下几个步骤:
- 选择基准问题
:选择一个公认的难解问题作为基准问题。 - 构造归约
:设计一个多项式时间算法,将基准问题转换为目标问题。 - 验证归约
:证明转换后的目标问题确实能够解决原始的基准问题。
步骤详解
选择基准问题
基准问题一般是公认的难解问题,如NP完全问题、大整数分解问题或离散对数问题。这些问题被认为在现有计算能力下无法在多项式时间内解决。
构造归约
构造归约的过程需要设计一个算法,将基准问题转换为目标问题。这要求归约过程在多项式时间内完成,以保证转换的有效性。
验证归约
验证归约的过程需要证明:如果能够在多项式时间内解决目标问题,那么就能在多项式时间内解决基准问题。这一步是归约证明的核心,确保目标问题的难度不低于基准问题。
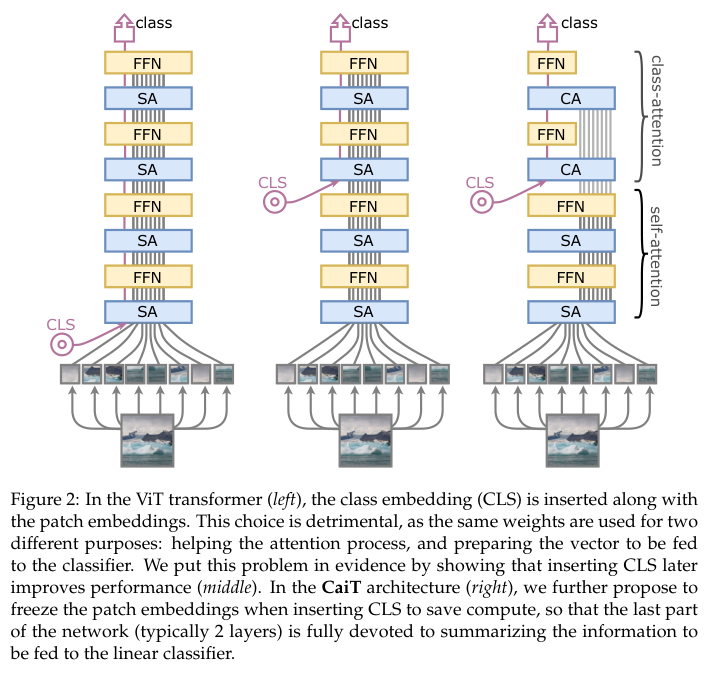
A[基准问题] -->|归约| B[目标问题];
B -->|证明难解| C[算法安全性]
多项式时间(Polynomial Time)
指算法运行时间是输入规模的某个多项式函数。多项式时间的算法被认为是有效率的,因为其运行时间随着输入规模的增加而成多项式增长。
NP完全问题(NP-complete Problem)
NP完全问题是一类计算上非常困难的问题,任何NP问题都能在多项式时间内归约为它。如果能够找到一个多项式时间内解决NP完全问题的算法,那么所有NP问题都能在多项式时间内解决。
离散对数问题(Discrete Logarithm Problem, DLP)
离散对数问题是指给定一个大质数
\(p\)
和一个生成元
\(g\)
,找到x使得
\(g^x \equiv h \mod p\)
。这是一个计算上公认的困难问题,广泛应用于密码学。
归约证明的应用
公钥加密中的应用
在公钥加密系统中,归约证明常用于证明加密算法的抗攻击性。例如,RSA加密算法的安全性可以归约为大整数分解问题的难度。如果有人能够在多项式时间内破解RSA加密,那么他也能在多项式时间内完成大整数分解,这在目前的计算理论中被认为是极其困难的。
数字签名中的应用
在数字签名方案中,归约证明可以用来证明签名的不可伪造性。例如,椭圆曲线数字签名算法(ECDSA)的安全性可以归约为椭圆曲线离散对数问题的难度。
实例分析
RSA加密算法的归约证明
RSA加密算法的安全性可以归约为大整数分解问题的难度。具体步骤如下:
- 选择基准问题
:大整数分解问题。 - 构造归约
:设计一个算法,将大整数分解问题转换为破解RSA加密。 - 验证归约
:证明如果能够破解RSA加密,那么就能够在多项式时间内完成大整数分解。
椭圆曲线数字签名算法(ECDSA)
ECDSA的安全性可以归约为椭圆曲线离散对数问题(ECDLP)。具体步骤如下:
- 选择基准问题
:椭圆曲线离散对数问题。 - 构造归约
:设计一个算法,将ECDLP转换为破解ECDSA签名。 - 验证归约
:证明如果能够伪造ECDSA签名,那么就能够在多项式时间内解决ECDLP。
归约证明的局限性
尽管归约证明是一个强大的工具,但它也存在一些局限性:
- 基准问题的依赖性
:归约证明依赖于基准问题的难解性。如果基准问题被攻破,那么基于该归约证明的安全性也会受到质疑。 - 归约过程的复杂性
:构造归约过程可能非常复杂,有时难以找到合适的基准问题和归约方法。 - 实际应用的挑战
:归约证明在理论上能保证安全性,但在实际应用中可能遇到未预见的挑战和漏洞。
结论
归约证明在密码学中起着至关重要的作用,通过将新问题归约为已知难解问题,我们能够更有信心地评估新算法的安全性。尽管归约证明有其局限性,但它依然是密码学研究中不可或缺的工具。希望本文通过详细的介绍和实例分析,能够帮助读者更好地理解归约证明的概念和应用。
PrimiHub
一款由密码学专家团队打造的开源隐私计算平台,专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。