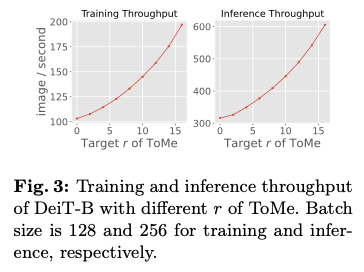
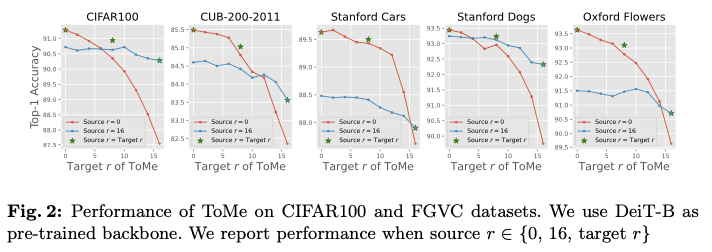
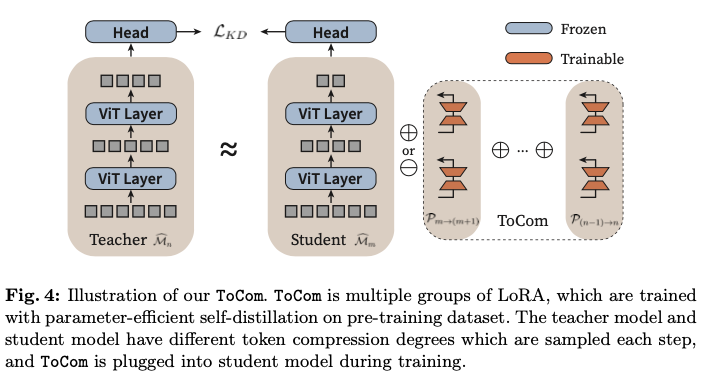
关于 Splay 树
前置芝士
$\LARGE {关于二叉搜索树及平衡树无聊的一大串子定义}$
二叉搜索树(BST树)
定义
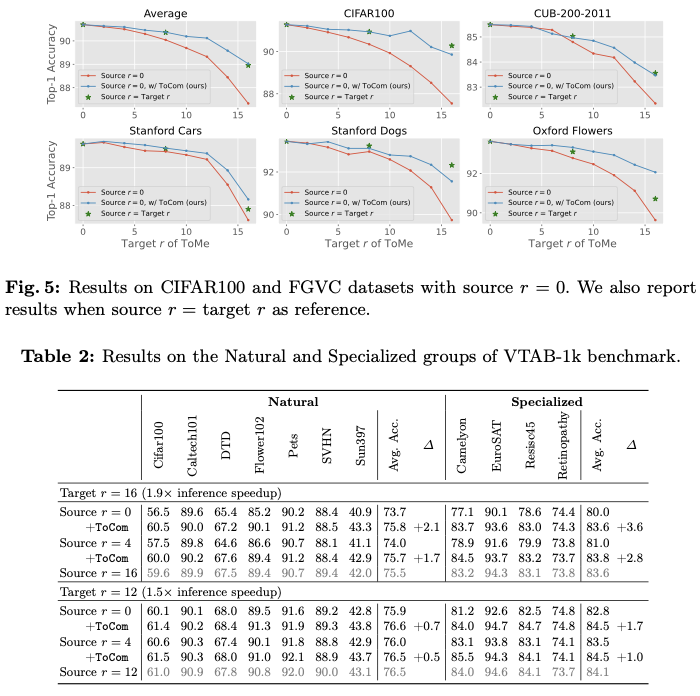
二叉搜索树是一种二叉树的树形数据结构,其定义如下:
空树是二叉搜索树。
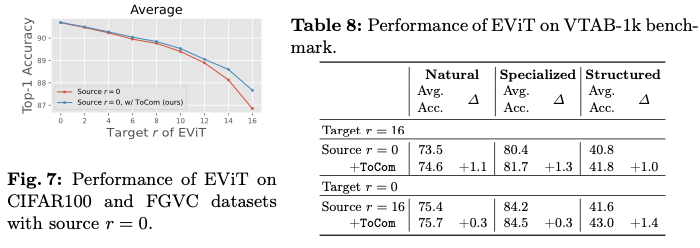
若二叉搜索树的左子树不为空,则其左子树上所有点的附加权值均小于其根节点的值。
若二叉搜索树的右子树不为空,则其右子树上所有点的附加权值均大于其根节点的值。
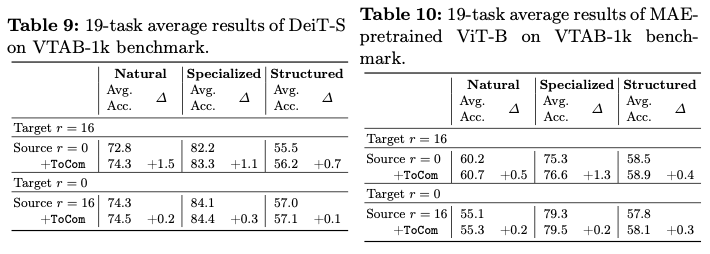
二叉搜索树的左右子树均为二叉搜索树。
复杂度
二叉搜索树上的基本操作所花费的时间与这棵树的高度成
\(\color{#40c0bb}{正比}\)
。对于一个有
\(n\)
个结点的二叉搜索树中,这些操作的最优时间复杂度为
\(O(\log n)\)
,最坏为
\(O(n)\)
。随机构造这样一棵二叉搜索树的
\(\color{#40c0bb}{期望高度}\)
为
\(O(\log n)\)
。
性质
其实也就是定义
设
\(x\)
是二叉搜索树中的一个结点。
如果
\(y\)
是
\(x\)
左子树中的一个结点,那么
\(y.key≤x.key\)
。
如果
\(y\)
是
\(x\)
右子树中的一个结点,那么
\(y.key≥x.key\)
。
在二叉搜索树中:
若任意结点的左子树不空,则左子树上所有结点的值均不大于它的根结点的值。
若任意结点的右子树不空,则右子树上所有结点的值均不小于它的根结点的值。
任意结点的左、右子树也分别为二叉搜索树。
用途
二叉搜索树通常可以高效地完成以下操作:
查找最小/最大值
搜索元素
插入一个元素
删除一个元素
求元素的排名
查找排名为 k 的元素
平衡树
定义
由二叉搜索树的复杂度分析可知:操作的复杂度与树的高度
\(h\)
有关。
那么我们可以通过一定操作维持树的高度(平衡性)来降低操作的复杂度,这就是
\(\color{#40c0bb}{平衡树}\)
。
\(\color{#40c0bb} \large \textbf{平衡性}\)
通常指每个结点的左右子树的高度之差的绝对值(平衡因子)最多为
\(1\)
。
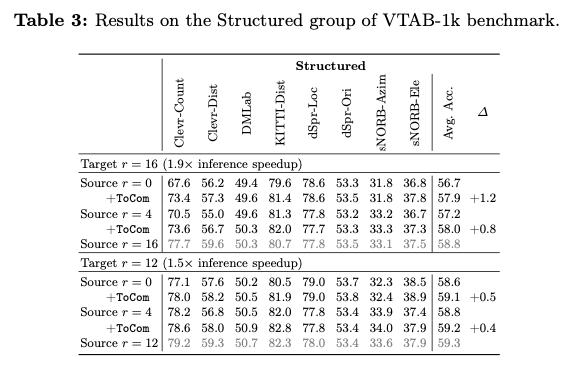
平衡的调整过程——树旋转
定义
树旋转是在二叉树中的一种子树调整操作, 每一次旋转并
\(\color{#40c0bb}{不影响}\)
对该二叉树进行
\(\color{#40c0bb}{中序遍历}\)
的结果。
树旋转通常应用于需要调整树的局部平衡性的场合。树旋转包括两个不同的方式,分别是
\(\color{#40c0bb}{左旋(Left Rotate 或者 zag)}\)
和
\(\color{#40c0bb}{右旋(Right Rotate 或者 zig)}\)
。 两种旋转呈镜像,而且互为逆操作。
具体操作
右旋
对于结点
\(A\)
的右旋操作是指:将
\(A\)
的左孩子
\(B\)
向右上旋转,代替
\(A\)
成为根节点,将
\(A\)
结点向右下旋转成为
\(B\)
的右子树的根结点,
\(B\)
的原来的右子树变为
\(A\)
的左子树。
左旋
完全同理

其实你只需要知道二叉搜索树的几条基本性质即可:
每个结点都满足左子树的结点的值都
小于
自己的值,右子树的结点的值都
大于
自己的值,
左右子树也是二叉搜索树
。中序遍历二叉搜索树可以得到一个由这棵树的所有结点的值组成的
有序
序列。(即所有的值排序后的结果)
正片
背景
不难发现
\(BST树\)
的一种极端情况:
\(\color{#40c0bb}{退化情况}\)
这种
毒瘤
数据让时间复杂度从
\(O(log(n))\)
退化到了恐怖的
\(O(n)\)
于是就有各种各样的科学家们,开始思考人生,丧心病狂地创造出了各种优化BST的方法...
Splay
定义
啥是
\(Splay\)
?
她实际上就是一种可以旋转的平衡树。
她可以通过
Splay/伸展操作
不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,能够在均摊
\(O(\log n)\)
时间内完成插入,查找和删除操作,并且保持平衡而不至于退化成链。
原理&实现
节点维护信息
| rt | tot | fa[N] | ch[N][2] | val[N] | cnt[N] | sz[N] |
|---|---|---|---|---|---|---|
| 根 | 节点编号 | 父节点 | 子节点 左0右1 | 权值 | 节点大小 | 子树大小 |
基本操作
首先你要了解的就是一些基本操作:
- \(maintain(x)\)
:在改变节点位置后,将节点
\(x\)
的
\(\text{size}\)
更新。 - \(get(x)\)
:判断节点
\(x\)
是父亲节点的左儿子还是右儿子。 - \(clear(x)\)
:清空节点
\(x\)
。
void maintain(int x){
sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x];
}
bool get(int x){
return x==ch[fa[x]][1];
}
void clear(int x){
ch[x][0]=ch[x][1]=fa[x]=val[x]=sz[x]=cnt[x]=0;
}
很简单对吧?
接下来可就要上难度了。
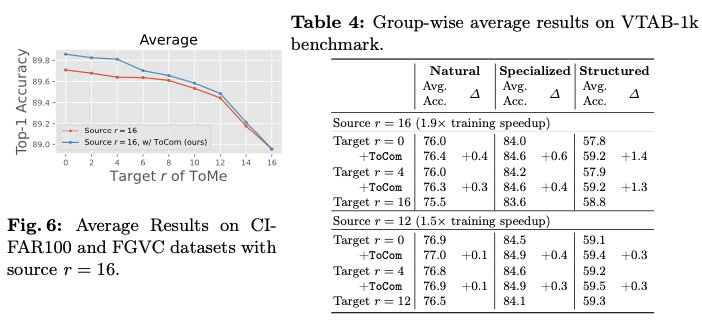
旋转操作(rotate)
由定义可知,我们要将某个节点旋转到根节点。
而要想知道怎么将一个节点旋转到根节点,首先要考虑怎么将她旋转到父亲节点。
当该节点为左儿子时
如图,方框表示子树,圆框表示节点

现在,我们要将
\(x\)
节点往上爬一层到他的父节点
\(y\)
,为了保证不改变中序遍历顺序,我们可以让
\(y\)
成为
\(x\)
的右儿子。
但是原来的
\(x\)
节点是有右儿子
\(B\)
的,显然我们要把
\(B\)
换一个位置才能达到目的。
我们知道:
\(x\)
节点的右子树必然是大于
\(x\)
节点的;
\(y\)
节点必然是大于
\(x\)
节点的右子树和
\(x\)
节点本身的(因为
\(x\)
节点及其右子树都是原来
\(y\)
的左子树,肯定比
\(y\)
小(根据二叉搜索树性质))
因此我们可以把
\(x\)
节点原来的右子树放在
\(y\)
的左儿子的位置上,达成目的。

实际上,这也就是
\(\color{#40c0bb}\textbf{右旋}\)
的原理。
当该节点为右儿子时
原理相同。
旋转为
通解
若节点
\(x\)
为
\(y\)
节点的位置
\(z\)
(
\(z=0\)
为左节点,
\(z=1\)
为右节点 )
将
\(y\)
节点放到
\(x\)
节点的
\(z \oplus 1\)
的位置.(也就是,
\(x\)
节点为
\(y\)
节点的右子树,那么
\(y\)
节点就放到左子树,
\(x\)
节点为
\(y\)
节点左子树,那么
\(y\)
节点就放到右子树位置)如果说
\(x\)
节点的
\(z \oplus 1\)
位置上,已经有节点,或者一棵子树,那么我们就将原来
\(x\)
节点
\(z \oplus 1\)
位置上的子树,放到
\(y\)
节点的位置
\(z\)
上面.
这里有个小口诀:“
左旋拎右左挂右,右旋拎左右挂左
”
看懂文字了,就可以尝试理解一下代码了。
实现
void rotate(int x){
int y=fa[x],z=fa[y],chk=get(x);
//y为x的父亲,z为x的爷爷,chk判断x是左儿子还是右儿子
ch[y][chk]=ch[x][chk^1];
if(ch[x][chk^1]) fa[ch[x][chk^1]]=y;
ch[x][chk^1]=y;
fa[y]=x;
fa[x]=z;
if(z) ch[z][y==ch[z][1]]=x;
maintain(y),maintain(x);
}
Splay操作
Splay(x,to)
是要将
\(x\)
节点旋转至
\(to\)
节点。
单旋
很暴力的办法,对于
\(x\)
节点,每次上旋至
\(fa[x]\)
,直到
\(to\)
节点。
但是,如果你真的这么写可能会
T成SB
被某些毒瘤数据卡成
\(n^2\)
所以不要看单旋简单好写,这里更推荐双旋的写法。
双旋
双旋的优化在于:
如果当前处于共线状态的话,那么先旋转
\(y\)
,再旋转
\(x\)
。这样可以强行让他们不处于共线状态,然后平衡这棵树.如果当前不是共线状态的话,那么只要旋转
\(x\)
即可。
void splay(int x,int goal=0){
if(goal==0) rt=x;
while(fa[x]!=goal){
int f=fa[x];
if(fa[fa[x]]!=goal){
rotate(get(x)==get(f)?f:x);
}
rotate(x);
}
}
查找操作
当然你也可以不写。
查找操作是因为查
\(k\)
的前驱后继时需要将
\(k\)
旋到根节点的位置。
实际上你也可以直接
splay(k,0)
或先插入
\(k\)
查询后再将它删去。
Splay也是一颗二叉搜索树,因此满足左侧都比他小,右侧都比他大。
因此只需要相应的往左/右递归即可。
void find(int x){
int u=root;
if(!u)return;//树空
while(t[u].ch[x>t[u].val]&&x!=t[u].val)
u=t[u].ch[x>t[u].val];
splay(u,0);
}
插入操作
- 如果树空了,则直接插入根并退出。
- 如果当前节点的权值等于
\(k\)
则增加当前节点的大小并更新节点和父亲的信息,将当前节点进行 Splay 操作。 - 否则按照二叉查找树的性质(左侧都比他小,右侧都比他大)向下找,找到空节点就插入即可。
void ins(int k){//insert
if(!rt){
val[++tot]=k;
cnt[tot]++;
rt=tot;
maintain(rt);
return;
}
int cur=rt,f=0;
while(1){
if(val[cur]==k){
cnt[cur]++;
maintain(cur);
maintain(f);
splay(cur);
break;
}
f=cur;
cur=ch[cur][val[cur]<k];
if(!cur){
val[++tot]=k;
cnt[tot]++;
fa[tot]=f;
ch[f][val[f]<k]=tot;
maintain(tot);
maintain(f);
splay(tot);
break;
}
}
}
查询
\(x\)
的排名
- 如果
\(x\)
比当前节点的权值小,向其左子树查找。 - 如果
\(x\)
比当前节点的权值大,将答案加上左子树(
\(size\)
)和当前节点(
\(cnt\)
)的大小,向其右子树查找。 - 如果
\(x\)
与当前节点的权值相同(已存在),将答案加
\(1\)
并返回。
int rk(int k){//the rank of "k"
int res=0,cur=rt;
while(1){
if(k<val[cur]){
cur=ch[cur][0];
}else{
res+=sz[ch[cur][0]];
if(!cur) return res+1;
if(k==val[cur]){
splay(cur);
return res+1;
}
res+=cnt[cur];
cur=ch[cur][1];
}
}
}
查询排名
\(x\)
的数
- 如果左子树非空且剩余排名
\(k\)
不大于左子树的大小
\(size\)
,那么向左子树查找。 - 否则将
\(k\)
减去左子树的和根的大小。如果此时
\(k\)
的值小于等于
\(0\)
,则返回根节点的权值,否则继续向右子树查找。
int kth(int k){//the number whose rank is "k"
int cur=rt;
while(1){
if(ch[cur][0] && k<=sz[ch[cur][0]]){
cur=ch[cur][0];
}else{
k-=cnt[cur]+sz[ch[cur][0]];
if(k<=0){
splay(cur);
return val[cur];
}
cur=ch[cur][1];
}
}
}
查询前驱&后继
前驱就是
\(x\)
的左子树中最右边的节点
后继就是
\(x\)
的右子树中最左边的节点
前驱
int pre(){//precursor
int cur=ch[rt][0];
if(!cur) return cur;
while(ch[cur][1]) cur=ch[cur][1];
splay(cur);
return cur;
}
后继
其实就是查前驱的反面
int nxt(){//next or successor
int cur=ch[rt][1];
if(!cur) return cur;
while(ch[cur][0]) cur=ch[cur][0];
splay(cur);
return cur;
}
查前驱后继有好多种写法,如果想偷懒只写一遍就可以酱紫
int prenxt(int x,int k){//0 pre 1 nxt
find(x);
int cur=rt;
if(!k && val[cur]<x) return cur;
if(k && val[cur]>x) return cur;
cur=ch[cur][k];
while(ch[cur][!k]){
cur=ch[cur][!k];
}
return cur;
}
删除操作
首先将
\(x\)
旋转到根的位置。
如果
\(cnt[x]>1\)
(有不止一个
\(x\)
),那么将
\(cnt[x] - 1\)
并退出。否则,合并它的左右两棵子树即可。
void del(int k){//delete
rk(k);
if(cnt[rt]>1){
cnt[rt]--;
maintain(rt);
return;
}
if(!ch[rt][0] && !ch[rt][1]){//树空
clear(rt);
rt=0;
return;
}
if(!ch[rt][0]){
int cur=rt;
rt=ch[rt][1];
fa[rt]=0;
clear(cur);
return;
}
if(!ch[rt][1]){
int cur=rt;
rt=ch[rt][0];
fa[rt]=0;
clear(cur);
return;
}
int cur=rt,x=pre();
fa[ch[cur][1]]=x;
ch[x][1]=ch[cur][1];
clear(cur);
maintain(rt);
}
那么恭喜你,你已经学完了Splay的基本操作。
至于区间翻转什么的...
下次丕定
Code
Elaina's Code
struct Slpay{
int rt;//根
int tot;//节点编号
int fa[N];//父节点
int ch[N][2];//子节点 左0右1
int val[N];//权值
int cnt[N];//节点大小
int sz[N];//子树大小
void maintain(int x){
sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x];
}
bool get(int x){
return x==ch[fa[x]][1];
}
void clear(int x){
ch[x][0]=ch[x][1]=fa[x]=val[x]=sz[x]=cnt[x]=0;
}
void rotate(int x){
int y=fa[x],z=fa[y],chk=get(x);
ch[y][chk]=ch[x][chk^1];
if(ch[x][chk^1]) fa[ch[x][chk^1]]=y;
ch[x][chk^1]=y;
fa[y]=x;
fa[x]=z;
if(z) ch[z][y==ch[z][1]]=x;
maintain(y);
maintain(x);
}
void splay(int x,int goal=0){
if(goal==0) rt=x;
while(fa[x]!=goal){
int f=fa[x];
if(fa[fa[x]]!=goal){
rotate(get(x)==get(f)?f:x);
}
rotate(x);
}
}
void ins(int k){//insert
if(!rt){
val[++tot]=k;
cnt[tot]++;
rt=tot;
maintain(rt);
return;
}
int cur=rt,f=0;
while(1){
if(val[cur]==k){
cnt[cur]++;
maintain(cur);
maintain(f);
splay(cur);
break;
}
f=cur;
cur=ch[cur][val[cur]<k];
if(!cur){
val[++tot]=k;
cnt[tot]++;
fa[tot]=f;
ch[f][val[f]<k]=tot;
maintain(tot);
maintain(f);
splay(tot);
break;
}
}
}
int rk(int k){//the rank of "k"
int res=0,cur=rt;
while(1){
if(k<val[cur]){
cur=ch[cur][0];
}else{
res+=sz[ch[cur][0]];
if(!cur) return res+1;
if(k==val[cur]){
splay(cur);
return res+1;
}
res+=cnt[cur];
cur=ch[cur][1];
}
}
}
int kth(int k){//the number whose rank is "k"
int cur=rt;
while(1){
if(ch[cur][0] && k<=sz[ch[cur][0]]){
cur=ch[cur][0];
}else{
k-=cnt[cur]+sz[ch[cur][0]];
if(k<=0){
splay(cur);
return val[cur];
}
cur=ch[cur][1];
}
}
}
int pre(){//precursor
int cur=ch[rt][0];
if(!cur) return cur;
while(ch[cur][1]) cur=ch[cur][1];
splay(cur);
return cur;
}
int nxt(){//next or successor
int cur=ch[rt][1];
if(!cur) return cur;
while(ch[cur][0]) cur=ch[cur][0];
splay(cur);
return cur;
}
void del(int k){//delete
rk(k);
if(cnt[rt]>1){
cnt[rt]--;
maintain(rt);
return;
}
if(!ch[rt][0] && !ch[rt][1]){
clear(rt);
rt=0;
return;
}
if(!ch[rt][0]){
int cur=rt;
rt=ch[rt][1];
fa[rt]=0;
clear(cur);
return;
}
if(!ch[rt][1]){
int cur=rt;
rt=ch[rt][0];
fa[rt]=0;
clear(cur);
return;
}
int cur=rt,x=pre();
fa[ch[cur][1]]=x;
ch[x][1]=ch[cur][1];
clear(cur);
maintain(rt);
}
void find(int x){
int cur=rt;
if(!cur) return;
while(ch[cur][x>val[cur]]&&x!=val[cur]){
cur=ch[cur][x>val[cur]];
}
splay(cur,0);
}
int get_pre(int x){
find(x);
int cur=rt;
if(val[cur]<x) return cur;
cur=ch[cur][0];
while(ch[cur][1]){
cur=ch[cur][1];
}
return cur;
}
int get_nxt(int x){
find(x);
int cur=rt;
if(val[cur]>x) return cur;
cur=ch[cur][1];
while(ch[cur][0]){
cur=ch[cur][0];
}
return cur;
}
int prenxt(int x,int k){//0 pre 1 nxt
find(x);
int cur=rt;
if(!k && val[cur]<x) return cur;
if(k && val[cur]>x) return cur;
cur=ch[cur][k];
while(ch[cur][!k]){
cur=ch[cur][!k];
}
return cur;
}
}tr;
signed main(){
int m=rd;
while(m--){
int opt=rd,x=rd;
if(opt==1){
tr.ins(x);
}else if(opt==2){
tr.del(x);
}else if(opt==3){
printf("%lld\n",tr.rk(x));
}else if(opt==4){
printf("%lld\n",tr.kth(x));
}else if(opt==5){
tr.ins(x),printf("%lld\n",tr.val[tr.pre()]),tr.del(x);
}else{
tr.ins(x),printf("%lld\n",tr.val[tr.nxt()]),tr.del(x);
}
}
return Elaina;
}
学了这么久 奖励你张图吧
才不是我自己想看