书接上回,今天和大家一起动手来自己实现树。
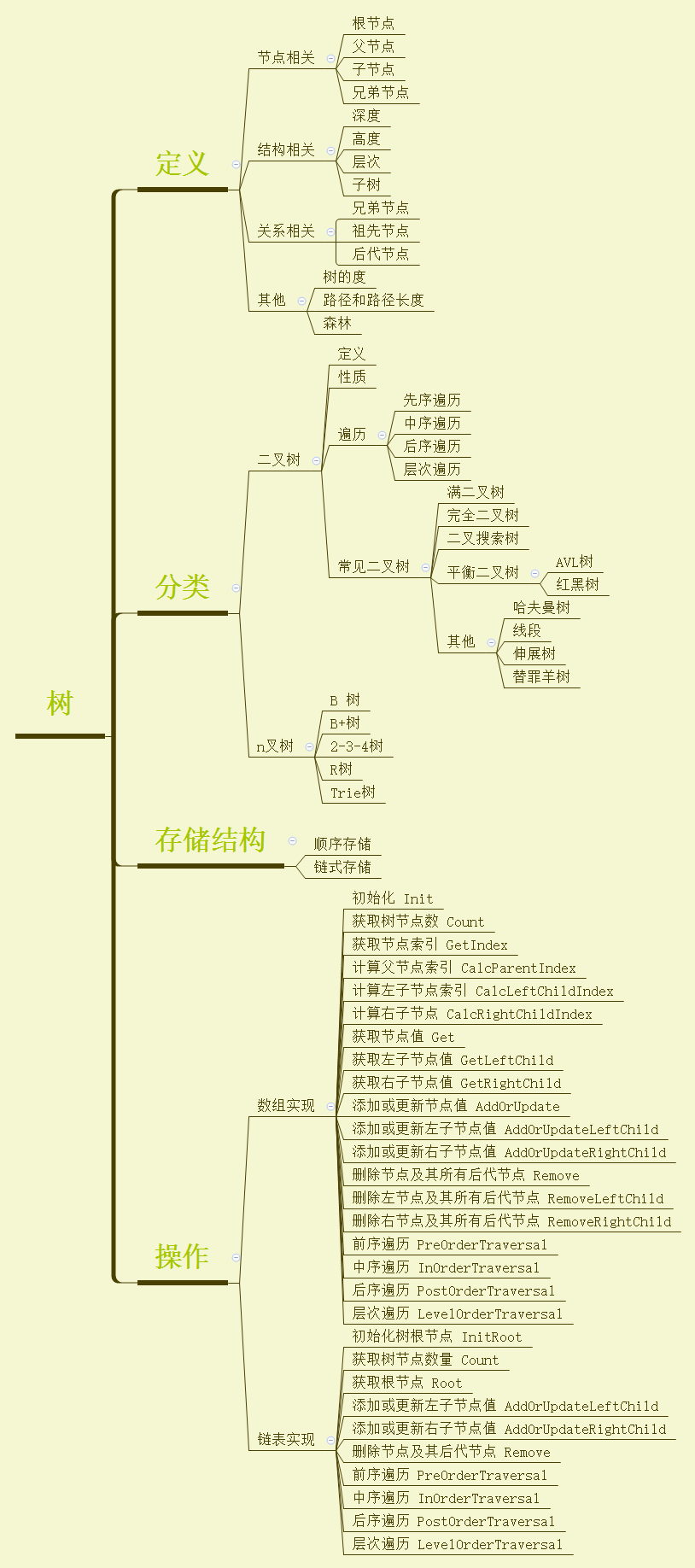
相信通过前面的章节学习,大家已经明白树是什么了,今天我们主要针对二叉树,分别使用顺序存储和链式存储来实现树。
01
、数组实现
我们在上一节中说过,如果从树的顶层开始从上到下,从左到右,对每个节点按顺序进行编号,根节点为1作为起始,则有节点编号i,其左子节点编号为2i,其右子节点编号为2i+1。但是我们知道数组的索引是从0开始,因此如果我们用数组实现二叉树,那么我们可以把上面的编号改为从0开始,因此可以得到如下结论:
节点编号:i;
其左子节点编号:2i+1;
其右子节点编号:2i+2;
1、初始化 Init
初始化主要是指定树节点容量,创建指定容量的数组。
//初始化树为指定容量
public MyselfTreeArray<T> Init(int capacity)
{
//初始化指定长度数组用于存放树节点元素
_array = new T[capacity];
//返回树
return this;
}
2、获取树节点数 Count
树节点数可以通过内部数组长度直接获取。
//树节点数量
public int Count
{
get
{
return _array.Length;
}
}
3、获取节点索引 GetIndex
获取节点索引主要是为了把节点值转为索引值,因为我们是使用数组实现,元素的操作更多依赖索引。其实我们还有其他方案来处理获取索引的方式,比如可以通过设计元素对象使其包含索引字段,这样其实操作起来更为方便。下面我们还是用最直接获取的方法作为演示。
//返回指定数据的索引
public int GetIndex(T data)
{
if (data == null)
{
return -1;
}
//根据值查找索引
return Array.IndexOf(_array, data);
}
4、计算父节点索引 CalcParentIndex
该方法用于实现通过子节点索引计算父节点索引,无论左子节点还是右子节点,使用下面一个公式就可以了,代码如下:
//根据子索引计算父节点索引
public int CalcParentIndex(int childIndex)
{
//应用公式计算父节点索引
var parentIndex = (childIndex + 1) / 2 - 1;
//检查索引是否越界
if (childIndex <= 0 || childIndex >= _array.Length
|| parentIndex < 0 || parentIndex >= _array.Length)
{
return -1;
}
//返回父节点索引
return parentIndex;
}
5、计算左子节点索引 CalcLeftChildIndex
该方法用于根据父节点索引计算左子节点索引。
//根据父节点索引计算左子节点索引
public int CalcLeftChildIndex(int parentIndex)
{
//应用公式计算左子节点索引
var leftChildIndex = 2 * parentIndex + 1;
//检查索引是否越界
if (leftChildIndex <= 0 || leftChildIndex >= _array.Length
|| parentIndex < 0 || parentIndex >= _array.Length)
{
return -1;
}
//返回左子节点索引
return leftChildIndex;
}
6、计算右子节点 CalcRightChildIndex
该方法用于根据父节点索引计算右子节点索引。
//根据父节点索引计算右子节点索引
public int CalcRightChildIndex(int parentIndex)
{
//应用公式计算右子节点索引
var rightChildIndex = 2 * parentIndex + 2;
//检查索引是否越界
if (rightChildIndex <= 0 || rightChildIndex >= _array.Length
|| parentIndex < 0 || parentIndex >= _array.Length)
{
return -1;
}
//返回右子节点索引
return rightChildIndex;
}
7、获取节点值 Get
该方法通过节点索引获取节点值,如果索引越界则报错。
//通过节点索引获取节点值
public T Get(int index)
{
//检查索引是否越界
if (index < 0 || index >= _array.Length)
{
throw new IndexOutOfRangeException("无效索引");
}
//返回节点值
return _array[index];
}
8、获取左子节点值 GetLeftChild
该方法是通过节点索引获取其左节点值,首先获取左子节点索引,再取左子节点值。
//通过节点索引获取其左子节点值
public T GetLeftChild(int parentIndex)
{
//获取左子节点索引
var leftChildIndex = CalcLeftChildIndex(parentIndex);
//检查索引是否越界
if (leftChildIndex < 0)
{
throw new IndexOutOfRangeException("无效索引");
}
//返回左子节点值
return _array[leftChildIndex];
}
9、获取右子节点值 GetRightChild
该方法是通过节点索引获取其右节点值,首先获取右子节点索引,再取右子节点值。
//通过节点索引获取其右子节点值
public T GetRightChild(int parentIndex)
{
//获取右子节点索引
var rightChildIndex = CalcRightChildIndex(parentIndex);
//检查索引是否越界
if (rightChildIndex < 0)
{
throw new IndexOutOfRangeException("无效索引");
}
//返回右子节点值
return _array[rightChildIndex];
}
10、添加或更新节点值 AddOrUpdate
该方法是通过节点索引添加或更新节点值,因为数组初始化的时候已经有了默认值,因此添加或者更新节点值就是直接给数组元素赋值,如果索引越界则报错。
//通过节点索引添加或更新节点值
public void AddOrUpdate(int index, T data)
{
//检查索引是否越界
if (index < 0 || index >= _array.Length)
{
throw new IndexOutOfRangeException("无效索引");
}
//更新值
_array[index] = data;
}
11、添加或更新左子节点值 AddOrUpdateLeftChild
该方法根据节点值添加或更新其左子节点值,首先通过节点值找到其索引,然后通过其索引计算出其左子节点索引,索引校验成功后,直接更新左子节点值。
//通过节点值添加或更新左子节点值
public void AddOrUpdateLeftChild(T parent, T left)
{
//获取节点索引
var parentIndex = GetIndex(parent);
//获取左子节点索引
var leftChildIndex = CalcLeftChildIndex(parentIndex);
//检查索引是否越界
if (leftChildIndex < 0)
{
throw new IndexOutOfRangeException("无效索引");
}
//更新值
_array[leftChildIndex] = left;
}
12、添加或更新右子节点值 AddOrUpdateRightChild
该方法根据节点值添加或更新其右子节点值,首先通过节点值找到其索引,然后通过其索引计算出其右子节点索引,索引校验成功后,直接更新右子节点值。
//通过节点值添加或更新右子节点值
public void AddOrUpdateRightChild(T parent, T right)
{
//获取节点索引
var parentIndex = GetIndex(parent);
//获取左子节点索引
var rightChildIndex = CalcRightChildIndex(parentIndex);
//检查索引是否越界
if (rightChildIndex < 0)
{
throw new IndexOutOfRangeException("无效索引");
}
//更新值
_array[rightChildIndex] = right;
}
13、删除节点及其所有后代节点 Remove
该方法通过节点索引删除其自身以及其所有后代节点,删除后代节点需要左右子节点分别递归调用方法自身。
//通过节点索引删除节点及其所有后代节点
public void Remove(int index)
{
//非法索引直接跳过
if (index < 0 || index >= _array.Length)
{
return;
}
//清除节点值
_array[index] = default;
//获取左子节点索引
var leftChildIndex = CalcLeftChildIndex(index);
//递归删除左子节点及其所有后代
Remove(leftChildIndex);
//获取右子节点索引
var rightChildIndex = CalcRightChildIndex(index);
//递归删除右子节点及其所有后代
Remove(rightChildIndex);
}
14、删除左节点及其所有后代节点 RemoveLeftChild
该方法通过节点值删除其左节点以及其左节点所有后代节点,首先通过节点值获取节点索引,然后计算出左子节点索引,最后通过调用删除节点Remove方法完成删除。
//通过节点值删除其左节点及其所有后代节点
public void RemoveLeftChild(T parent)
{
//获取节点索引
var parentIndex = GetIndex(parent);
//获取左子节点索引
var leftChildIndex = CalcLeftChildIndex(parentIndex);
//检查索引是否越界
if (leftChildIndex < 0)
{
throw new IndexOutOfRangeException("无效索引");
}
//删除左子节点及其所有后代
Remove(leftChildIndex);
}
15、删除右节点及其所有后代节点 RemoveRightChild
该方法通过节点值删除其右节点以及其右节点所有后代节点,首先通过节点值获取节点索引,然后计算出右子节点索引,最后通过调用删除节点Remove方法完成删除。
//通过节点值删除其右节点及其所有后代节点
public void RemoveRightChild(T parent)
{
//获取节点索引
var parentIndex = GetIndex(parent);
//获取右子节点索引
var rightChildIndex = CalcRightChildIndex(parentIndex);
//检查索引是否越界
if (rightChildIndex < 0)
{
throw new IndexOutOfRangeException("无效索引");
}
//删除右子节点及其所有后代
Remove(rightChildIndex);
}
16、前序遍历 PreOrderTraversal
前序遍历的核心思想就是先打印树的根节点,然后再打印树的左子树,最后打印树的右子树。
//前序遍历
public void PreOrderTraversal(int index = 0)
{
//非法索引直接跳过
if (index < 0 || index >= _array.Length)
{
return;
}
//打印
Console.Write(_array[index]);
//获取左子节点索引
var leftChildIndex = CalcLeftChildIndex(index);
//打印左子树
PreOrderTraversal(leftChildIndex);
//获取右子节点索引
var rightChildIndex = CalcRightChildIndex(index);
//打印右子树
PreOrderTraversal(rightChildIndex);
}
17、中序遍历 InOrderTraversal
中序遍历的核心思想就是先打印树的左子树,然后再打印树的根节点,最后打印树的右子树。
//中序遍历
public void InOrderTraversal(int index = 0)
{
//非法索引直接跳过
if (index < 0 || index >= _array.Length)
{
return;
}
//获取左子节点索引
var leftChildIndex = CalcLeftChildIndex(index);
//打印左子树
InOrderTraversal(leftChildIndex);
//打印
Console.Write(_array[index]);
//获取右子节点索引
var rightChildIndex = CalcRightChildIndex(index);
//打印右子树
InOrderTraversal(rightChildIndex);
}
18、后序遍历 PostOrderTraversal
后序遍历的核心思想就是先打印树的左子树,然后再打印树的右子树,最后打印树的根节点。
//后序遍历
public void PostOrderTraversal(int index = 0)
{
//非法索引直接跳过
if (index < 0 || index >= _array.Length)
{
return;
}
//获取左子节点索引
var leftChildIndex = CalcLeftChildIndex(index);
//打印左子树
PostOrderTraversal(leftChildIndex);
//获取右子节点索引
var rightChildIndex = CalcRightChildIndex(index);
//打印右子树
PostOrderTraversal(rightChildIndex);
//打印
Console.Write(_array[index]);
}
19、层次遍历 LevelOrderTraversal
层次遍历的核心思想是借助队列,从根节点开始,从上到下,从左到右,先入列后等待后续打印,然后出列后立即打印,同时把此节点的左右子节点按顺序加入队列,循环往复直至所有元素打印完成。
//层次遍历
public void LevelOrderTraversal()
{
//创建一个队列用于层次遍历
var queue = new Queue<int>();
//先把根节点索引0入队
queue.Enqueue(0);
//只有队列中有值就一直处理
while (queue.Count > 0)
{
//出列,取出第一个节点索引
var currentIndex = queue.Dequeue();
//打印第一个节点值
Console.Write(_array[currentIndex]);
//获取左子节点索引
int leftChildIndex = CalcLeftChildIndex(currentIndex);
// 如果左子节点存在,将其索引加入队列
if (leftChildIndex >= 0)
{
queue.Enqueue(leftChildIndex);
}
//获取右子节点索引
int rightChildIndex = CalcRightChildIndex(currentIndex);
// 如果右子节点存在,将其索引加入队列
if (rightChildIndex >= 0)
{
queue.Enqueue(rightChildIndex);
}
}
}
02
、链表实现
链表实现通用性会更强,基本可以实现所有的树结构,同时操作也更方便了,下面我们还是以二叉树的实现为例做演示。
1、初始化树根节点 InitRoot
在初始化树根节点前需要定义好链表的节点,其包含数据域和左右子节点,同时在树种还需要维护根节点以及节点数量两个私有字段。
public class MyselfTreeNode<T>
{
//数据域
public T Data { get; set; }
////左子节点
public MyselfTreeNode<T> Left { get; set; }
//右子节点
public MyselfTreeNode<T> Right { get; set; }
public MyselfTreeNode(T data)
{
Data = data;
Left = null;
Right = null;
}
}
public class MyselfTreeLinkedList<T>
{
//根节点
private MyselfTreeNode<T> _root;
//树节点数量
private int _count;
//初始化树根节点
public MyselfTreeLinkedList<T> InitRoot(T root)
{
_root = new MyselfTreeNode<T>(root);
//树节点数量加1
_count++;
//返回树
return this;
}
}
2、获取树节点数量 Count
树节点数量可以通过私有字段_count直接返回。
//获取树节点数量
public int Count
{
get
{
return _count;
}
}
3、获取根节点 Root
根节点可以通过私有字段_root直接返回。
//获取根节点
public MyselfTreeNode<T> Root
{
get
{
return _root;
}
}
4、添加或更新左子节点值 AddOrUpdateLeftChild
该方法是通过节点添加或更新其左子节点值。
//通过指定节点添加或更新左子节点值
public void AddOrUpdateLeftChild(MyselfTreeNode<T> parent, T left)
{
if (parent.Left != null)
{
//更节点值
parent.Left.Data = left;
return;
}
//添加节点
parent.Left = new MyselfTreeNode<T>(left);
//节点数量加1
_count++;
}
5、添加或更新右子节点值 AddOrUpdateRightChild
该方法是通过节点添加或更新其右子节点值。
//通过指定节点添加或更新右子节点元素
public void AddOrUpdateRightChild(MyselfTreeNode<T> parent, T right)
{
if (parent.Right != null)
{
//更节点值
parent.Right.Data = right;
return;
}
//添加节点
parent.Right = new MyselfTreeNode<T>(right);
//节点数量加1
_count++;
}
6、删除节点及其后代节点 Remove
该方法通过节点删除其自身以及其所有后代节点,需要递归删除左右子节点及其所有后代节点。
//通过指定节点删除节点及其后代节点
public void Remove(MyselfTreeNode<T> node)
{
if (node.Left != null)
{
//递归删除左子节点的所有后代
Remove(node.Left);
}
if (node.Right != null)
{
//递归删除右子节点的所有后代
Remove(node.Right);
}
//删除节点
node.Data = default;
//节点数量减1
_count--;
}
7、前序遍历 PreOrderTraversal
核心思想和数组实现一样。
//前序遍历
public void PreOrderTraversal(MyselfTreeNode<T> node)
{
//打印
Console.Write(node.Data);
if (node.Left != null)
{
//打印左子树
PreOrderTraversal(node.Left);
}
if (node.Right != null)
{
//打印右子树
PreOrderTraversal(node.Right);
}
}
8、中序遍历 InOrderTraversal
核心思想和数组实现一样。
//中序遍历
public void InOrderTraversal(MyselfTreeNode<T> node)
{
if (node.Left != null)
{
//打印左子树
InOrderTraversal(node.Left);
}
//打印
Console.Write(node.Data);
if (node.Right != null)
{
//打印右子树
InOrderTraversal(node.Right);
}
}
9、后序遍历 PostOrderTraversal
核心思想和数组实现一样。
//后序遍历
public void PostOrderTraversal(MyselfTreeNode<T> node)
{
if (node.Left != null)
{
//打印左子树
PostOrderTraversal(node.Left);
}
if (node.Right != null)
{
//打印右子树
PostOrderTraversal(node.Right);
}
//打印
Console.Write(node.Data);
}
10、层次遍历 LevelOrderTraversal
核心思想和数组实现一样。
//层次遍历
public void LevelOrderTraversal()
{
//创建一个队列用于层次遍历
Queue<MyselfTreeNode<T>> queue = new Queue<MyselfTreeNode<T>>();
//先把根节点入队
queue.Enqueue(_root);
//只有队列中有值就一直处理
while (queue.Count > 0)
{
//出列,取出第一个节点
var node = queue.Dequeue();
//打印第一个节点值
Console.Write(node.Data);
// 如果左子节点存在将其加入队列
if (node.Left != null)
{
queue.Enqueue(node.Left);
}
// 如果右子节点存在将其加入队列
if (node.Right != null)
{
queue.Enqueue(node.Right);
}
}
}
注
:测试方法代码以及示例源码都已经上传至代码库,有兴趣的可以看看。
https://gitee.com/hugogoos/Planner