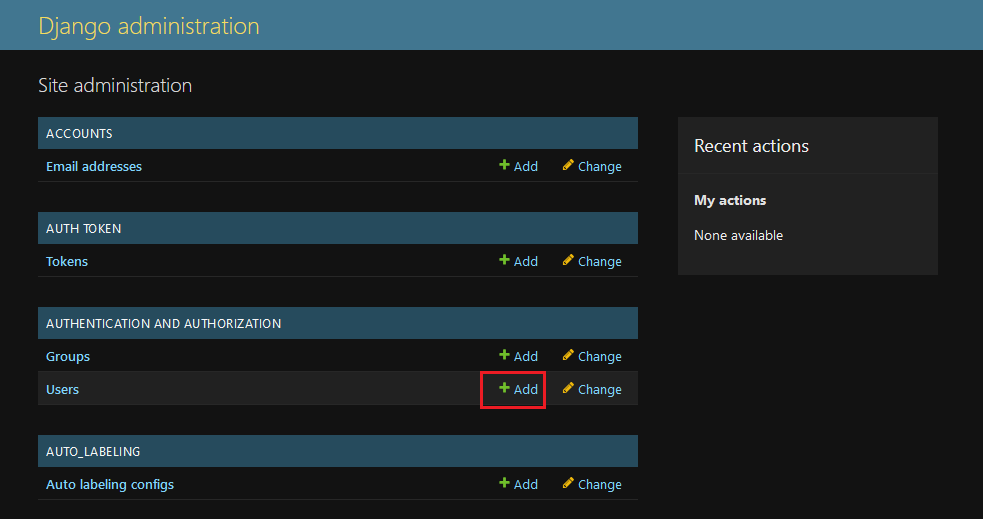
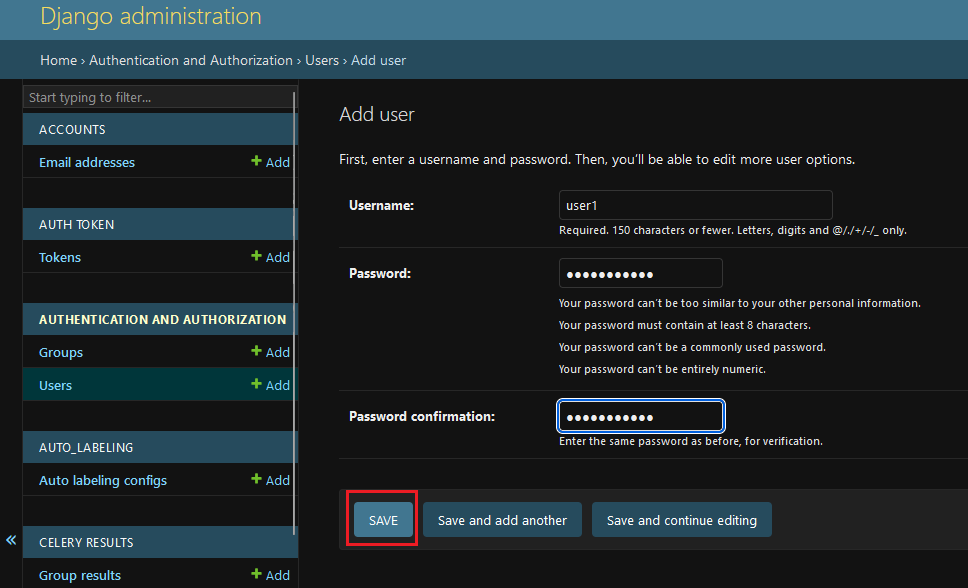
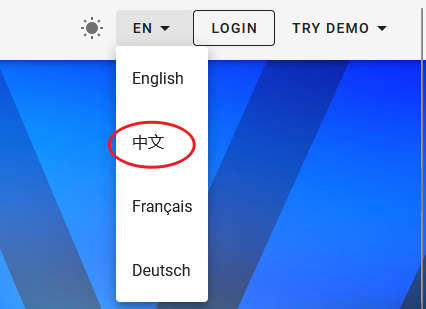
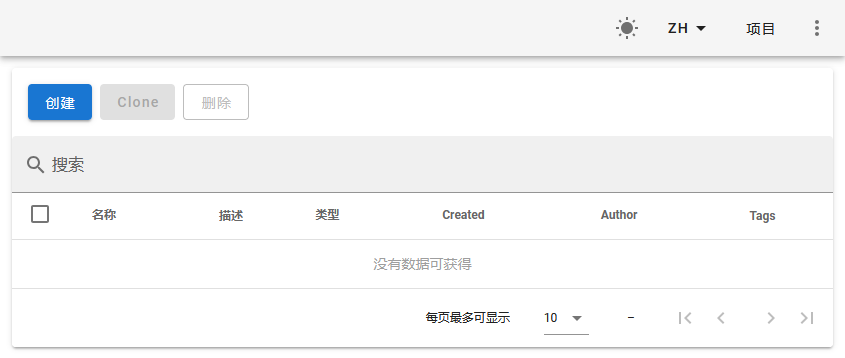
DIKI:清华提出基于残差的可控持续学习方案,完美保持预训练知识 | ECCV'24
本研究解决了领域-类别增量学习问题,这是一个现实但富有挑战性的持续学习场景,其中领域分布和目标类别在不同任务中变化。为应对这些多样化的任务,引入了预训练的视觉-语言模型(
VLMs
),因为它们具有很强的泛化能力。然而,这也引发了一个新问题:在适应新任务时,预训练
VLMs
中编码的知识可能会受到干扰,从而损害它们固有的零样本能力。现有方法通过在额外数据集上对
VLMs
进行知识蒸馏来解决此问题,但这需要较大的计算开销。为了高效地解决此问题,论文提出了分布感知无干扰知识集成(
DIKI
)框架,从避免信息干扰的角度保留
VLMs
的预训练知识。具体而言,设计了一个完全残差机制,将新学习的知识注入到一个冻结的主干网络中,同时对预训练知识产生最小的不利影响。此外,这种残差特性使分布感知集成校准方案成为可能,明确控制来自未知分布的测试数据的信息植入过程。实验表明,
DIKI
超过了当前最先进的方法,仅使用
0.86%
的训练参数,并且所需的训练时间大幅减少。来源:晓飞的算法工程笔记 公众号,转载请注明出处
论文: Mind the Interference: Retaining Pre-trained Knowledge in Parameter Efficient Continual Learning of Vision-Language Models

Introduction
监督学习技术在对所有数据完全访问的情况下训练网络,这可能导致在扩展网络以获取新任务知识时缺乏灵活性。持续学习(
CL
)作为一种解决方案应运而生,使得模型能够在陆续到达的数据上进行持续训练,同时保留所学的信息。传统的
CL
设置一般考虑的只新引入的类别或领域分布的变化,这称为类别增量学习和领域增量学习。然而,只考虑一种增量的现有工作限制了它们在复杂现实场景中的适用性。
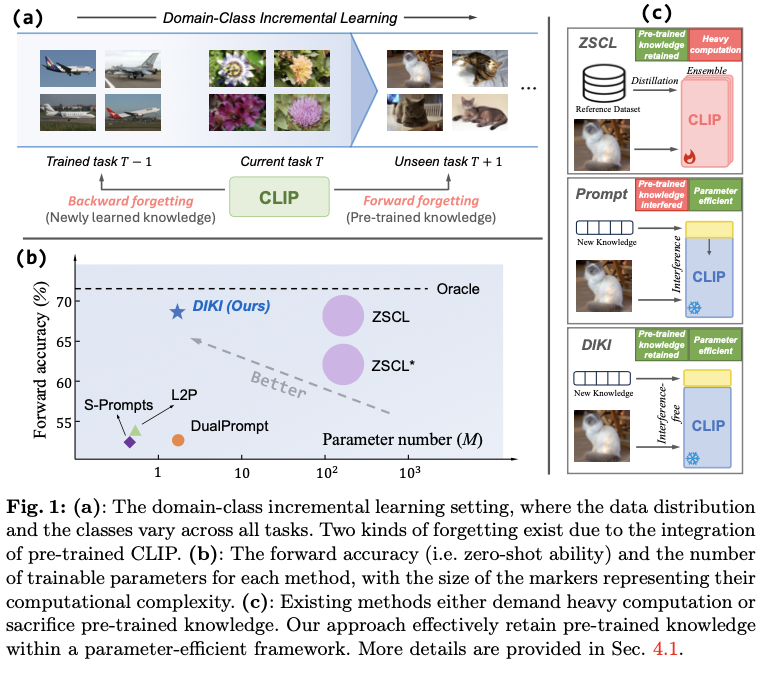
考虑一个更具挑战性的领域-类别增量学习(
DCIL
)设置,在该设置中,领域数据分布和待分类的类别在所有任务中可能不断变化,如图
1(a)
所示。在这种情况下,基于传统图像编码器的技术由于其不可扩展的分类头设计而无法实现。最近,对比训练的视觉-语言模型(
VLMs
)如
CLIP
的出现,使得解决这一要求高但实际的问题成为可能。
VLMs
是在大规模的图像-文本对上训练的,具有强大的零样本泛化能力,可以识别几乎无限的类别,应对这种严重的任务变化场景。
然而,使用视觉-语言模型引入了增量训练的新挑战。传统的持续学习方案旨在防止模型遗忘先前学习的知识,这被称为向后遗忘(忘记微调的知识)。现有的研究探讨了正则化机制、复习缓冲区和架构设计在减轻向后遗忘方面的潜力,并取得了令人鼓舞的成果。然而,当这些方法应用于视觉-语言模型时,出现了一种不同形式的灾难性遗忘:模型往往会遗忘在预训练阶段所学的知识,从而妨碍其强大的零样本泛化能力。这个问题被称为向前遗忘(忘记预训练的知识),因为它发生在
VLMs
对未知分布数据进行“向前”预测时。图
1(a)
展示了这两种遗忘类型。
最近的工作
ZSCL
尝试解决
CLIP
上的向前遗忘问题,引入了一个大规模的参考数据集来进行知识蒸馏,并结合了权重集成方案。然而,这种方法需要大量的计算和外部数据,在实际场景中可能不可行。同时,现有的基于
VLM
的参数高效持续学习方法主要利用提示调整机制,未能保留预训练知识,并导致零样本能力下降,如图
1
(b)所示。论文将这个问题归因于信息干扰:新引入的任务特定参数可能会干扰预训练知识。这些方法的示意图如图
1(c)
所示。
为了以计算和参数高效的方式缓解
VLMs
的向前遗忘问题,论文引入了分布感知无干扰知识融合(
DIKI
)框架。具体而言,将任务特定信息注入到冻结的
VLM
中,以便为每个任务高效地存储已学习的知识。
论文的贡献总结为三点:
- 引入了参数高效的
DIKI
,以在
DCIL
设置下保留
VLM
中的预训练知识。它解决了信息干扰问题,降低了对大量计算和外部数据的需求。 - 为了缓解向前遗忘,
DIKI
以完全残差的方式植入新知识,保持预训练知识不受干扰。凭借这种残差特性,进一步集成了分布感知融合校准,以提高在未见任务上的性能。 - 综合实验表明,与以前的方法相比,
DIKI
以仅
0.86%
的训练参数和显著更少的训练时间实现了最先进的性能。
Preliminaries
Continual learning protocol
持续学习旨在以顺序方式学习不同的任务,同时不忘记之前学到的知识。考虑到
\(N\)
个顺序到达的任务
\(\left[ \mathcal{T}^1, \mathcal{T}^2, \cdots, \mathcal{T}^N \right]\)
,每个任务
\(\mathcal{T}^i\)
包含一个数据集
\(D^i=\{x^i_j, y^i_j\}_{j=1}^{N^i}\)
,其中
\(x^i_j\)
是一幅图像,
\(y^i_j\)
是当前数据集中对应的独热标签,
\(N^i\)
是图像样本的数量。此外,还包括一个类名集合
\(C^i=\{c^i_j\}_{j=1}^{N_{c}^i}\)
,将标签索引连接到
VLMs
使用的类别名称。
与之前的类别和领域增量学习设置不同,本研究强调了一种更实际的持续学习设置:领域-类别增量学习(
DCIL
)。在这个设置中,领域分布和需要识别的类别在不同任务之间不断变化,即
\(C^i \neq C^j\)
和
\(\mathbb{P}(D^i) \neq \mathbb{P}(D^j)\)
,对于
\(i \neq j\)
,其中
\(\mathbb{P}\)
表示任务数据集的数据分布。
Vision-language models
在具有挑战性的领域-类别增量学习(
DCIL
)设置中,训练基于普通图像编码器的模型,如
ResNets
和
ViTs
,对于增量学习强烈变化的领域和类别并不实用。因此,引入了预训练的视觉-语言模型,因为它们具有强大的零样本迁移能力。
CLIP
包含一个图像编码器
\(f\)
和一个文本编码器
\(g\)
,它们被训练用于生成成对图像-文本样本的紧密对齐特征。在推理时,
\(f\)
首先将输入图像
\(x\)
编码为特征向量
\(f(x)\)
。与此同时,潜在的类名被嵌入到一个模板中,例如“一个{
\(c\)
}的照片”,然后由
\(g\)
编码以形成文本嵌入
\(\{t_j\}_{j=1}^{N_c}\)
。模型的预测通过图像嵌入与所有文本嵌入之间的最大相似性得分来确定
\(s_j = \Braket{f(x), t_j}\)
,其中
\(\Braket{\cdot, \cdot}\)
表示余弦相似度。
Task-specific prompt learning
一系列研究开始探索在持续学习中参数高效微调的潜力,常见的做法是为每个任务学习和存储一组轻量级提示,在持续学习阶段形成一个“提示池”,表示为:
\mathbf{P}=\{P_1, P_2, \cdots, P_N\},\ \ \text{where}\ P_i\in \mathbb{R}^{l\times d},
\end{equation}
\]
其中
\(N\)
是任务编号,
\(l\)
和
\(d\)
分别是提示的长度和特征嵌入的维度。
在推理时,选择经过良好训练的提示并将附加到预训练的冻结模型上,以恢复学习到的知识。假设
\(\mathbf{x_e}\in \mathbb{R}^{L\times d}\)
是
Transformer
层
\(h\)
的特征嵌入,那么可以将提示添加到
\(\mathbf{x_e}\)
前面,以生成提示输入:
\mathbf{x_p} = \left[P_s^1; P_s^2; \cdots; P_s^l; \mathbf{x_e}\right] \in \mathbb{R}^{(l+L)\times d},
\end{equation}
\]
其中
\(\{P_s^i\in \mathbb{R}^{d}\}_{i=1}^l\)
是选定提示
\(P_s\)
的嵌入向量,
\(;\)
表示沿着
token
长度维度的连接操作。通过这种植入的知识,生成了更好的图像和文本特征嵌入,并且最终的分类准确率得到了提高。
上述提到的提示选择过程是通过查询-键匹配来实现的。在持续训练阶段,通过最大化余弦相似度或应用聚类算法来学习每个任务的平均特征表示
\(\mathbf{I}=\{I^i\}_{i=1}^N\)
。当测试样本
\(\mathbf{x}\)
到来时,进行键查找操作:
\label{eq_matching}
I_s = {\arg \max}_{I^i\sim \mathbf{I}}\Braket{f(\mathbf{x}), I^i}.
\end{equation}
\]
通过最相关的键
\(I_s\)
,选择相应的提示
\(P_s\)
并将其附加到冻结模型上,执行推理过程。
Methodology
Interference-free Knowledge Integration
Is prepending the best choice?
尽管将提示预先添加到输入
tokens
的方法因其实现简单而被广泛使用,但论文发现它们面临两个方面的问题。
- 将提示与输入
tokens
进行连接会导致它们在注意力过程中相互作用,从而影响预训练知识的提取。当测试样本来自模型学习提示时的分布时,适应后的模型可以保持相对令人满意的结果。然而,一旦遇到分布发生改变的样本,这种干扰可能导致模型性能下降,并损失其重要的零样本泛化能力,造成前向遗忘问题。 - 简单地预先添加提示不可避免地增加了所有
Transformer
块的
token
长度,这在许多有
token
长度限制的场景中并不理想。另外,它的可扩展性有限:较长的提示上下文可能会使文本编码器忽视重要的类别名称,从而导致文本嵌入表示不佳。
上述问题的存在表明,基于提示调优的方法并不满足“残差属性”:期望学习到的参数应该是与冻结主干并行的残差路径,补充新的知识而不影响关键的预训练知识。因此,论文提出了一种无干扰知识整合(
Interference-free Knowledge Integration
,
IKI
)方案,以最小化噪声的方式将新学习的知识注入到预训练的
VLM
中。
IKI mechanism
论文不再为每个任务训练一系列预先添加的提示向量,而是关注自注意力机制的修改,这遵循了自然语言处理领域中广泛使用的参数高效微调方法。回想一下,在
Transformer
层
\(h\)
中,对输入
tokens
\(\mathbf{x_e}\in \mathbb{R}^{L\times d}\)
进行的多头自注意力机制。为了简化,省略了多头设计,仅考虑单头情况,这可以自然扩展到多头场景。输入
tokens
首先通过线性投影转换为查询
\(Q\)
、键
\(K\)
和价值
\(V\)
矩阵:
Q_e = \mathbf{x_e}W^Q + b^Q; K_e = \mathbf{x_e}W^K + b^K; V_e = \mathbf{x_e}W^V + b^V,
\end{equation}
\]
其中
\(W\in \mathbb{R}^{d\times d}\)
和
\(b\in \mathbb{R}^{d}\)
是预训练参数。然后,执行自注意力计算,通过以下方式生成输出矩阵:
O_L = \text{Attn}(Q_e, K_e)V_e = \text{softmax}(\frac{Q_eK_e^T}{\sqrt{d}})V_e\ \ \in \mathbb{R}^{L\times d},
\end{equation}
\]
其中
\(\text{softmax}(\mathbf{z})_i = \frac{\exp{(\mathbf{z_i})}}{\sum_j\exp{(\mathbf{z_j})}}\)
可以约束注意力结果中的元素
\(\text{Attn}(Q_e, K_e)\in \mathbb{R}^{L\times L}\)
的总和为一。
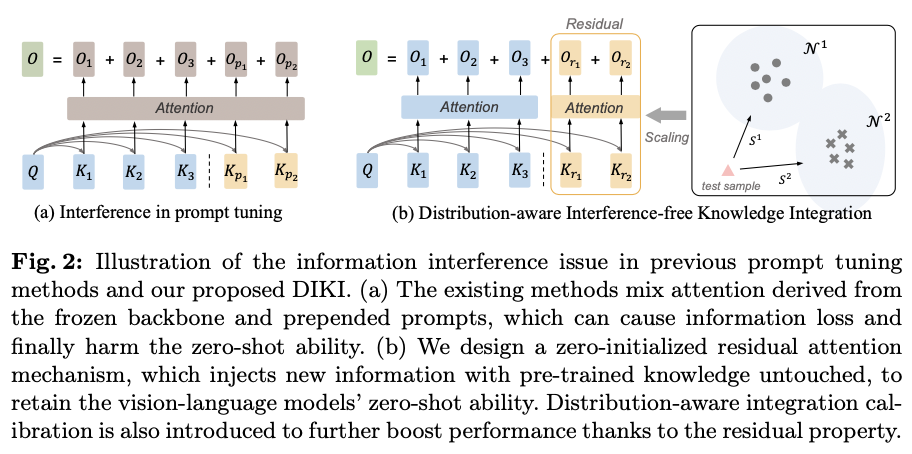
普通的提示调优方法将可训练的提示添加到输入
tokens
中,将
\(\mathbf{x_e}\in \mathbb{R}^{L\times d}\)
扩展为
\(\mathbf{x_p}\in \mathbb{R}^{(l+L)\times d}\)
。然后,将计算
\(Q_{p}K_{p}^T\in \mathbb{R}^{(l+L)\times (l+L)}\)
并传递给
softmax
函数。在
softmax
计算内部,输入
tokens
和提示的注意力分数相互作用并相互影响,导致预训练知识的不可避免损失,如图
2(a)
所示。
为了解决这个问题,论文分别计算输入
tokens
内的自注意力和提示与输入
tokens
之间的交叉注意力,如图
2(b)
所示。换句话说,只训练一个残差注意力分支,保持现有的注意力分数不变。通过新引入的键
\(K_r\)
和值
\(V_r\)
,残差注意力分支的输出可以表示为:
\label{eq:res_attn}
O_r = \text{softmax}(\frac{Q_eK_r^T}{\sqrt{d}})V_r, \text{where}\ K_r,V_r\in \mathbb{R}^{l\times d}.
\end{equation}
\]
这里,残差输出
\(O_r\in \mathbb{R}^{L\times d}\)
通过与原始输出
\(O_L\)
的正交路径得出,对原始注意力过程没有影响。最后,通过加法将存储在
\(O_r\)
中的学习知识植入输出中。在持续训练阶段,更新可学习的键
\(K_r\)
和值
\(V_r\)
,而不是常用的提示
\(P\)
。请注意,为了保持序列长度不变,没有引入任何查询参数。
理想情况下,一个理想的残差块在未在下游数据集上进行训练之前,应该不会影响原始分支,比如在初始化时。广泛使用的方式用均匀或正态分布初始化提示,这会在没有学习到任何知识的情况下向预训练的
VLMs
中注入随机噪声。具体而言,通过将参数
\(V_r\)
初始化为零,强制残差注意力加法成为一个恒等函数:
O = O_L+O_r^{\text{init}} = O_L+\text{softmax}(\frac{Q_eK_r^T}{\sqrt{d}})\mathbf{[0]}^{l\times d} = O_L.
\end{equation}
\]
注意,论文仅在开始时将值
\(V_r^{\text{init}}\)
限制为零,同时保持
\(K_r\)
随机初始化。这是因为将
\(K_r\)
和
\(V_r\)
都初始化为零矩阵会阻止
\(K_r\)
通过梯度更新,从而使
\(V_r\)
陷入到具有相同值的向量中。
由于零初始化更像是一种选择而非技术,一些研究在各种任务中采用了它。然而,这些工作利用零初始化来确保稳定和渐进的训练机制,而在
DCIL
场景中并不存在这一顾虑。论文认为,零初始化对于残差注意力设计是至关重要的,它可以以最小的噪声将新知识注入到预训练的
VLMs
中。
Distribution-aware Integration Calibration
Observations
在推理时,会执行公式
3
中描述的查询-键匹配机制,以检索适合当前测试样本的学习提示。这种方法是针对传统的持续学习设置而设计的,仅考虑了向后遗忘。然而,当面对来自未见领域的数据时,这种简单的匹配设计被强制执行,从而为测试样本分配一个相对相似的任务,尽管它们之间存在显著的分布差距。
得益于
IKI
的残差设计,与之前的方法相比,现在可以在这种不匹配的场景中引入更少的噪声。然而,当训练和测试分布之间的差异增加时,模型在某种程度上的性能下降是不可避免的,这会损害
VLMs
在预训练阶段所学到的零样本能力。
ZSCL
通过蒸馏来解决这个问题。他们构建了一个包含来自
ImageNet
的
100,000
张图像的参考数据集,以在每个训练步骤中将原始
CLIP
的预训练知识蒸馏到当前模型中,明确进行复习以避免遗忘。这种方法可能有效,但它依赖于大规模存储和高计算资源,从而在实际环境中显得不切实际。
一个直观的解决方案是控制知识植入模型的程度。然而,之前基于前置的提示调整技术只有两个选择:要么追加学习到的提示,要么不对原始
CLIP
模型进行任何修改。得益于
IKI
的优雅残差特性,现在可以控制这一并行分支的能力。
DIKI: calibrate the integration with distribution
为了确定测试样本属于已学习任务的可能性,为每个任务维护一个特征分布,而不是一个单一的关键向量。在这里,论文简单地应用多元高斯分布,并发现效果良好。形式上,在训练阶段为任务
\(i\)
构建一个
\(\mathcal{N}^i(\mathbf{\mu}^i, \mathbf{\Sigma}^i)\)
:
\begin{gathered}
\mathbf{\mu}^i = \mathbb{E}_{\mathbf{x}^i_j \sim D^i}[f(\mathbf{x}^i_j)], \ \ \ \mathbf{\Sigma}^i = \mathbb{E}_{\mathbf{x}^i_j \sim D^i}[(f(\mathbf{x}^i_j)-\mathbf{\mu}^i)^T(f(\mathbf{x}^i_j)-\mathbf{\mu}^i)],
\end{gathered}
\end{equation}
\]
其中
\(f(\mathbf{x}^i_j)\)
是由冻结编码器提取的图像特征。通过这些估计的分布,可以计算每个
\(\mathcal{N}^i\)
中测试样本被抽取的可能性。在这里,计算概率密度的对数作为输入
\(\mathbf{x}\)
在每个学习任务上的评分函数:
\begin{split}
S^i &= \log \varphi(f(\mathbf{x}); \mathbf{\mu}^i, \mathbf{\Sigma}^i) \\
&= - \frac{1}{2}[ (f(\mathbf{x})-\mathbf{\mu}^i)^T(\mathbf{\Sigma}^i)^{-1}(f(\mathbf{x})-\mathbf{\mu}^i) + d\log 2\pi + \log |\mathbf{\Sigma}^i|) ],
\end{split}
\end{equation}
\]
其中
\(\varphi\)
是概率密度函数。
直观上,得分较高的样本
\(S^i\)
更可能是从任务
\(i\)
中抽取的,并且应该引入参数
\(K_r^i, V_r^i\)
以进行模型预测。此外,还应该考虑到输入样本
\(\mathbf{x}\)
可能来自某些新的分布,如果所有
\(S^i\)
都很低,这一点就得到了暗示。因此,利用最大得分
\(\hat{S}=\max_{i\in [1,N]}S^{i}\)
来加权残余注意力输出:
\label{eq:final_output}
O = O_L+\mathcal{M}(\hat{S})O_r,
\end{equation}
\]
其中
\(\mathcal{M}\)
是一个映射函数,将得分
\(\hat{S}\)
缩放到范围
\([0,1]\)
。在这里,论文发现简单的
Sigmoid
函数
\(\sigma(x)=\frac{1}{1+e^{-x}}\)
在此效果很好。得益于这种基于分布感知的集成校准机制,
VLMs
的预训练零样本能力可以更好地保留,通过对不熟悉的图像分配较低的权重,进一步解决了前向遗忘的问题。
Experiments
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】