前言

gRPC 是一种高性能、开源的远程过程调用（RPC）框架，它基于 Protocol Buffers（protobuf）定义服务，并使用 HTTP/2 协议进行通信。

新建项目

新建解决方案GrpcDemo

新建webapi项目GrpcServer作为grpc服务端项目

添加包

    <PackageReference Include="Grpc.AspNetCore" Version="2.67.0" />
    <PackageReference Include="Grpc.Tools" Version="2.67.0">

新建文本文件greeter.proto

syntax = "proto3";

option csharp_namespace = "GrpcServer";

package greet;

// The greeting service definition.
service Greeter {
  // Sends a greeting
  rpc SayHello (HelloRequest) returns (HelloReply);
}

// The request message containing the user's name.
message HelloRequest {
  string name = 1;
}

// The response message containing the greetings.
message HelloReply {
  string message = 1;
}

编辑GrpcServer项目文件，添加

新建类GreeterService.cs

using Grpc.Core;

namespace GrpcServer
{
    public class GreeterService : Greeter.GreeterBase
    {
        private readonly ILogger<GreeterService> _logger;
        public GreeterService(ILogger<GreeterService> logger)
        {
            _logger = logger;
        }

        public override Task<HelloReply> SayHello(HelloRequest request, ServerCallContext context)
        {
            return Task.FromResult(new HelloReply
            {
                Message = "Hello " + request.Name
            });
        }
    }
}

修改Program.cs

using GrpcServer;

var builder = WebApplication.CreateBuilder(args);

// Add services to the container.

builder.Services.AddControllers();
// Learn more about configuring Swagger/OpenAPI at https://aka.ms/aspnetcore/swashbuckle
builder.Services.AddEndpointsApiExplorer();
builder.Services.AddSwaggerGen();

builder.Services.AddGrpc();

var app = builder.Build();

app.MapGrpcService<GreeterService>();

// Configure the HTTP request pipeline.
if (app.Environment.IsDevelopment())
{
    app.UseSwagger();
    app.UseSwaggerUI();
}

app.UseHttpsRedirection();

app.UseAuthorization();

app.MapControllers();

app.Run();

就是添加下面两行代码

builder.Services.AddGrpc();

app.MapGrpcService<GreeterService>();

新建grpc客户端项目GrpcClient

添加包

    <PackageReference Include="Google.Protobuf" Version="3.28.3" />
    <PackageReference Include="Grpc.Net.Client" Version="2.67.0" />
    <PackageReference Include="Grpc.Tools" Version="2.67.0">

复制服务器端端的greeter.proto到客户端项目

编辑GrpcClient项目文件，加

编辑Program.cs文件

using Grpc.Net.Client;
using GrpcClient;

using var channel = GrpcChannel.ForAddress("https://localhost:7052");
var client = new Greeter.GreeterClient(channel);
var reply = await client.SayHelloAsync(
                  new HelloRequest { Name = "wxy" });
Console.WriteLine("Greeting: " + reply.Message);
Console.WriteLine("Press any key to exit...");
Console.ReadKey();

7052改成你的服务器端运行端口

结果展示

运行服务器端

运行客户端

作者

吴晓阳（手机：13736969112微信同号）

书接上回，我们继续来聊聊.NET9和C#13带来的新变化。

01
、Linq新方法 CountBy 和 AggregateBy

引入了新的方法 CountBy 和 AggregateBy后，可以在不经过GroupBy 分配中间分组的情况下快速完成复杂的聚合操作，同时方法命名也非常直观，可以大大提升工作效率。

我们先以CountBy为例，简单实现一个小功能，统计不同年龄有多少人，代码如下：

public class Student
{
    public string Name { get; set; }
    public int Age { get; set; }
}
public void CountByExample()
{
    var students = new List<Student>
    {
        new Student { Name = "小明", Age = 10 },
        new Student { Name = "小红", Age = 12 },
        new Student { Name = "小华", Age = 10 },
        new Student { Name = "小亮", Age = 11 }
    };
    //统计不同年龄有多少人，两个版本实现
    //.NET 9 之前
    var group = students.GroupBy(x => x.Age);
    foreach (var item in group)
    {
        Console.WriteLine($"年龄为：{item.Key}，有：{item.Count()} 人。");
    }
    //.NET 9
    foreach (var student in students.CountBy(c => c.Age))
    {
        Console.WriteLine($"年龄为：{student.Key}，有：{student.Value} 人。");
    }
}

通过代码可以发现，老版本中必须先调用GroupBy分组再调用Count统计才可完成，而现在只需要调用CountBy即可。

我们再以AggregateBy为例子，看看新老版本中如何计算每个班级中各自学生总年龄，代码如下：

public class Student
{
    public string Name { get; set; }
    public string Grade { get; set; }
    public int Age { get; set; }        
}
public void AggregateByExample()
{
    var students = new List<Student>
    {
        new Student { Name = "小明", Grade = "一班", Age = 10 },
        new Student { Name = "小红", Grade = "二班", Age = 12 },
        new Student { Name = "小华", Grade = "一班", Age = 10 },
        new Student { Name = "小亮", Grade = "二班", Age = 11 }
    };
    //统计每个班级各自学生总年龄，两个版本实现
    //.NET 9 之前
    var old = students
       .GroupBy(stu => stu.Grade)
       .ToDictionary(group => group.Key, group => group.Sum(stu => stu.Age))
       .AsEnumerable();
    foreach (var item in old)
    {
        Console.WriteLine($"班级：{item.Key}，总年龄：{item.Value} 。");
    }
    //.NET 9
    foreach (var group in students.AggregateBy(c => c.Grade, 0, (acc, stu) => acc + stu.Age))
    {
        Console.WriteLine($"班级：{group.Key}，总年龄：{group.Value} 。");
    }
}

02
、序列化加强

在System.Text.Json中，.NET 9为序列化提供了新的选项和一个新的单例。

1、缩进选项

现在可以通过JsonSerializerOptions新属性IndentCharacter和IndentSize，自定义写入 JSON 的缩进字符和缩进大小。看看下面代码。

static void Main()
{
    var options = new JsonSerializerOptions
    {
        WriteIndented = true,
        IndentCharacter = '\t',
        IndentSize = 2,
        //处理中文乱码
        Encoder = JavaScriptEncoder.Create(UnicodeRanges.All)
    };
    var json = JsonSerializer.Serialize(
        new Student { Name = "小明", Grade = "一班", Age = 10 },
        options
    );
    Console.WriteLine(json);
    Console.ReadKey();
}

代码执行效果如下：

2、默认 Web 选项单例

在之前的版本中如果想要以小驼峰命名规则序列化对象可以配合JsonProperty特性实现。现在则可以直接通过JsonSerializerOptions.Web单例直接实现。

var json = JsonSerializer.Serialize(
    new Student { Name = "xiaoming", Grade = "yinianji", Age = 10 },
    JsonSerializerOptions.Web
);
Console.WriteLine(json);

代码执行效果如下：

03
、Task新方法Task.WhenEach

在.NET9之前，如果我们有一个任务列表，并希望每个任务完成后立刻处理它，那么我们只能通过不停的调用Task.WaitAny()方法来实现，现在.NET9引入了Task.WhenEach方法，以一种更优雅、更高效的方式处理这种情况。

因为Task.WhenEach 返回 IAsyncEnumerable<Task
>，因此可以配合await foreach语句在任务完成时对其进行迭代，下面我们一起看看示例。

async Task WhenEachAsync()
{
    //生成100个随机时间完成的任务列表
    var tasks = Enumerable.Range(1, 100)
                   .Select(async i =>
                   {
                       await Task.Delay(new Random().Next(1000, 5000));
                       return $"任务 {i} 完成";
                   })
                   .ToList();
    //.NET 9 之前
    while (tasks.Count > 0)
    {
        var completedTask = await Task.WhenAny(tasks);
        tasks.Remove(completedTask);
        Console.WriteLine(await completedTask);
    }
    //.NET 9
    await foreach (var completedTask in Task.WhenEach(tasks))
    {
        Console.WriteLine(await completedTask);
    }
}

04
、新的 TimeSpan.From* 重载

在.NET9之前TimeSpan类提供了几种From*方法，可以使用double类型来创建TimeSpan对象。但是，由于double是基于二进制的浮点格式，因此固有的不精确性可能会导致错误。

为了解决这个问题，.NET 9 添加了新的重载方法，可以使用整数创建TimeSpan对象。

如下面这段代码：

TimeSpan timeSpan1 = TimeSpan.FromSeconds(value: 101.832);
Console.WriteLine($"timeSpan1 = {timeSpan1}");
// timeSpan1 = 00:01:41.8319999
TimeSpan timeSpan2 = TimeSpan.FromSeconds(seconds: 101, milliseconds: 832);
Console.WriteLine($"timeSpan2 = {timeSpan2}");
// timeSpan2 = 00:01:41.8320000

05
、新的内置Swagger

从.NET9开始使用Scalar代替内置的Swagger（Swashbuckle），一方面是因为Swashbuckle项目维护不够积极，另一个方面也是内部希望更专业于OpenAPI的发展。不管原因如何，我们都要根据自己的情况做好选择。

下面我们来一起体验一下Scalar。

首先创建一个Web Api项目，然后安装Scalar.AspNetCore包，修改Prag代码如：

public static void Main(string[] args)
{
    var builder = WebApplication.CreateBuilder(args);
    builder.Services.AddControllers();
    builder.Services.AddOpenApi();
    var app = builder.Build();
    // scalar/v1
    app.MapScalarApiReference(); 
    app.MapOpenApi();
    app.UseAuthorization();
    app.MapControllers();
    app.Run();
}

然后我们添加一个简单的控制器，添加增删改查四个方法，代码如下：

[ApiController]
[Route("[controller]")]
public class OrdersController : ControllerBase
{
    private static readonly string[] Summaries = new[]
    {
        "Freezing", "Bracing", "Chilly", "Cool", "Mild", "Warm", "Balmy", "Hot", "Sweltering", "Scorching"
    };
    private readonly ILogger<OrdersController> _logger;
    public OrdersController(ILogger<OrdersController> logger)
    {
        _logger = logger;
    }
    [HttpGet(Name = "")]
    public IEnumerable<Order> Get()
    {
        return Enumerable.Range(1, 5).Select(index => new Order
        {
            Date = DateOnly.FromDateTime(DateTime.Now.AddDays(index)),
            Price = Random.Shared.Next(-20, 55),
            Name = Summaries[Random.Shared.Next(Summaries.Length)]
        })
        .ToArray();
    }
    [HttpPost(Name = "")]
    public bool Post(Order order)
    {
        return true;
    }
    [HttpPut(Name = "{id}")]
    public bool Put(string id, Order order)
    {
        return true;
    }
    [HttpDelete(Name = "{id}")]
    public bool Delete(string id)
    {
        return true;
    }
}

然后我们允许代码看看效果：

卖相还是相当惊艳的，左侧是接口列表，左下角可以切换黑白两种风格主题，右侧是接口详情，同时还配备了多种语言请求格式。

我们点击右下角Test Request测试一下获取接口。

可以在左边填写好参数，添加最上面的Send，会看到右下角请求结果。更详细复杂的应用大家可以自己摸索摸索。

注
：测试方法代码以及示例源码都已经上传至代码库，有兴趣的可以看看。
https://gitee.com/hugogoos/Planner

PPO算法是强化学习算法中目前应用最广的算法，虽然这个算法是2017年发表的，但是至今在整个AI领域下的agent子领域中这个算法都是最主要的强化学习算法（至少目前还没有之一），这个算法尤其在ChatGPT和人形机器人中起到了关键性的作用，可以说PPO算法是当前AI领域最为重要的算法之一（这个可以有之一，比如还有transformer等算法）。

下面给出NVIDIA公司和Google公司分别发布的PPO算法的实现：

NVIDIA公司的PPO算法实现源码地址：

https://openi.pcl.ac.cn/devilmaycry812839668/Isaac_rl_pytorch

Google公司的PPO算法实现的源码地址：

https://openi.pcl.ac.cn/devilmaycry812839668/google_brax_ppo_pytorch

因为PPO算法的论文是公开发表的，因此所有公司对于PPO算法的实现的核心基本都是一致的，但是由于所有公司都是根据原始论文自己重新编写的，因此不同的实现会导致一些细节上的不同，而细节上的不同是有可能导致算法性能上的表现有差异的，因此本文就以NVIDIA公司和Google公司的不同实现上来探究一下这种细节上的差距是否会影响算法的最终性能有较大变化。

为了便于分析，在
https://openi.pcl.ac.cn/devilmaycry812839668/google_brax_ppo_pytorch
中将NVIDIA公司的实现所用的trick形成了ppo_nvidia.py，而Google公司的实现细节形成了ppo_google.py，从而进行性能比较。

可以看到二者实现的主要区别在于loss函数中的critic的loss以及actor的advantage的计算部分，而在这里可以用两个函数的不同实现来表现，具体如下：

Google公司的实现：

  @torch.jit.export
  def compute_gae(self, truncation, termination, reward, values,
                  bootstrap_value):
    truncation_mask = 1 - truncation
    # Append bootstrapped value to get [v1, ..., v_t+1]
    values_t_plus_1 = torch.cat(
        [values[1:], torch.unsqueeze(bootstrap_value, 0)], dim=0)
    deltas = reward + self.discounting * (
        1 - termination) * values_t_plus_1 - values
    deltas *= truncation_mask

    acc = torch.zeros_like(bootstrap_value)
    vs_minus_v_xs = torch.zeros_like(truncation_mask)

    for ti in range(truncation_mask.shape[0]):
      ti = truncation_mask.shape[0] - ti - 1
      acc = deltas[ti] + self.discounting * (
          1 - termination[ti]) * truncation_mask[ti] * self.lambda_ * acc
      vs_minus_v_xs[ti] = acc

    # Add V(x_s) to get v_s.
    vs = vs_minus_v_xs + values
    vs_t_plus_1 = torch.cat([vs[1:], torch.unsqueeze(bootstrap_value, 0)], 0)
    advantages = (reward + self.discounting *
                  (1 - termination) * vs_t_plus_1 - values) * truncation_mask
    return vs, advantages

  @torch.jit.export
  def loss(self, td: Dict[str, torch.Tensor]):
    observation = self.normalize(td['observation'])
    policy_logits = self.policy(observation[:-1])
    baseline = self.value(observation)
    baseline = torch.squeeze(baseline, dim=-1)

    # Use last baseline value (from the value function) to bootstrap.
    bootstrap_value = baseline[-1]
    baseline = baseline[:-1]
    reward = td['reward'] * self.reward_scaling
    termination = td['done'] * (1 - td['truncation'])

    loc, scale = self.dist_create(td['logits'])
    behaviour_action_log_probs = self.dist_log_prob(loc, scale, td['action'])
    loc, scale = self.dist_create(policy_logits)
    target_action_log_probs = self.dist_log_prob(loc, scale, td['action'])

    with torch.no_grad():
      vs, advantages = self.compute_gae(
          truncation=td['truncation'],
          termination=termination,
          reward=reward,
          values=baseline,
          bootstrap_value=bootstrap_value)

    rho_s = torch.exp(target_action_log_probs - behaviour_action_log_probs)
    surrogate_loss1 = rho_s * advantages
    surrogate_loss2 = rho_s.clip(1 - self.epsilon,
                                 1 + self.epsilon) * advantages
    policy_loss = -torch.mean(torch.minimum(surrogate_loss1, surrogate_loss2))

    # Value function loss
    v_error = vs - baseline
    v_loss = torch.mean(v_error * v_error) * 0.5 * 0.5

    # Entropy reward
    entropy = torch.mean(self.dist_entropy(loc, scale))
    entropy_loss = self.entropy_cost * -entropy

    return policy_loss + v_loss + entropy_loss
  

nvidia公司的实现：

  @torch.jit.export
  def compute_gae(self, truncation, termination, reward, values,
                  bootstrap_value):
    truncation_mask = 1 - truncation
    # Append bootstrapped value to get [v1, ..., v_t+1]
    values_t_plus_1 = torch.cat(
        [values[1:], torch.unsqueeze(bootstrap_value, 0)], dim=0)
    deltas = reward + self.discounting * (
        1 - termination) * values_t_plus_1 - values
    deltas *= truncation_mask

    acc = torch.zeros_like(bootstrap_value)
    vs_minus_v_xs = torch.zeros_like(truncation_mask)

    for ti in range(truncation_mask.shape[0]):
      ti = truncation_mask.shape[0] - ti - 1
      acc = deltas[ti] + self.discounting * (
          1 - termination[ti]) * truncation_mask[ti] * self.lambda_ * acc
      vs_minus_v_xs[ti] = acc

    # Add V(x_s) to get v_s.
    vs = vs_minus_v_xs + values
    vs_t_plus_1 = torch.cat([vs[1:], torch.unsqueeze(bootstrap_value, 0)], 0)
    advantages = (reward + self.discounting *
                  (1 - termination) * vs_t_plus_1 - values) * truncation_mask
    return vs, advantages


  @torch.jit.export
  def compute_gae_nvidia(self, truncation, termination, reward, values,
                  bootstrap_value):
    truncation_mask = 1 - truncation
    # Append bootstrapped value to get [v1, ..., v_t+1]
    values_t_plus_1 = torch.cat(
        [values[1:], torch.unsqueeze(bootstrap_value, 0)], dim=0)
    deltas = reward + self.discounting * (
        1 - termination) * values_t_plus_1 - values
    deltas *= truncation_mask

    acc = torch.zeros_like(bootstrap_value)
    vs_minus_v_xs = torch.zeros_like(truncation_mask)

    for ti in range(truncation_mask.shape[0]):
      ti = truncation_mask.shape[0] - ti - 1
      acc = deltas[ti] + self.discounting * (
          1 - termination[ti]) * truncation_mask[ti] * self.lambda_ * acc
      vs_minus_v_xs[ti] = acc

    # Add V(x_s) to get v_s.
    vs = vs_minus_v_xs + values
    # vs_t_plus_1 = torch.cat([vs[1:], torch.unsqueeze(bootstrap_value, 0)], 0) ##### 后修改
    # advantages = (reward + self.discounting *                                 ##### 后修改
    #               (1 - termination) * vs_t_plus_1 - values) * truncation_mask
    # return vs, advantages                                                     ##### 后修改
    return vs, (vs_minus_v_xs - vs_minus_v_xs.mean())/(vs_minus_v_xs.std()+1e-8)##### 后修改
    return vs, (vs_minus_v_xs - vs_minus_v_xs.mean())/(vs_minus_v_xs.std()+1e-8)* truncation_mask##### 后修改


  @torch.jit.export
  def loss(self, td: Dict[str, torch.Tensor]):
    observation = self.normalize(td['observation'])
    policy_logits = self.policy(observation[:-1])
    new_baseline = self.value(observation[:-1])        ##### 后修改
    new_baseline = torch.squeeze(new_baseline, dim=-1) ##### 后修改
    # baseline = self.value(observation)
    # baseline = torch.squeeze(baseline, dim=-1)
    baseline = td["value"]                       ##### 后修改
    baseline = torch.squeeze(baseline, dim=-1)   ##### 后修改

    # Use last baseline value (from the value function) to bootstrap.
    bootstrap_value = baseline[-1]
    baseline = baseline[:-1]
    reward = td['reward'] * self.reward_scaling
    termination = td['done'] * (1 - td['truncation'])

    loc, scale = self.dist_create(td['logits'])
    behaviour_action_log_probs = self.dist_log_prob(loc, scale, td['action'])
    loc, scale = self.dist_create(policy_logits)
    target_action_log_probs = self.dist_log_prob(loc, scale, td['action'])

    with torch.no_grad():
      vs, advantages = self.compute_gae(
          truncation=td['truncation'],
          termination=termination,
          reward=reward,
          values=baseline,
          bootstrap_value=bootstrap_value)

    rho_s = torch.exp(target_action_log_probs - behaviour_action_log_probs)
    surrogate_loss1 = rho_s * advantages
    surrogate_loss2 = rho_s.clip(1 - self.epsilon,
                                 1 + self.epsilon) * advantages
    policy_loss = -torch.mean(torch.minimum(surrogate_loss1, surrogate_loss2))

    # Value function loss
    v_error = vs - new_baseline
    v_loss = torch.mean(v_error * v_error) * 0.5 * 0.5

    # Entropy reward
    entropy = torch.mean(self.dist_entropy(loc, scale))
    entropy_loss = self.entropy_cost * -entropy

    return policy_loss + v_loss + entropy_loss

可以看到，NVIDIA公司的实现中在actor的advantage的计算部分是严格按照PPO论文中的公式形式结合GAE后所组成的形式，其主要特点就是GAE是使用old policy下的value计算的，而与之对应的Google公司实现的版本中GAE部分是使用new policy下的value进行计算的，而Google公司的这种对advantage的实现方法是不符合PPO论文中的推导的。

Google公司的实现版本在计算出GAE后又将其加回到value中，然后按照TD(0)的计算公式再次计算，并用最后的计算值作为ppo算法中的advantage值。

在critic的loss计算中，虽然在原始的PPO论文中并没有给出这部分的实现，但是这部分的实现也是各家公司都有各自的具体实现，从Google和NVIDIA公司的实现中区别在于target_value的实现部分，由于都是critic_loss=MSE(target_value - value)**2，因此这部分只需要看具体的target_value的实现即可。而Google公司和NVIDIA公司的这部分实现都是在GAE的实现上加回到计算GAE时所使用的value从而得到target_value，由此可以看到这部分的实现上的区别和GAE实现的区别是一致的，那就是Google公司采用的事new_policy下的value，而NVIDIA公司则是按照ppo论文推导中的那样使用的是old_policy下的value。

通过上面的分析可以看到NVIDIA公司和Google公司在PPO算法的实现核心上有较大的出入，其中NVIDIA公司的实现版本更为贴近于PPO论文中的数学推导，而Google公司中的实现更像是一种写错了的diy代码，但是就如同AI算法中的很多算法都是由于写错后发现还不错，能work，然后才发明出来一样（比如dropout算法等就是写错代码后回溯一下，review一看发现效果更好才出现的），那么Google公司这种在原始论文的数学推导的基础上自己DIY的那种实现，并且这种DIY是没有理论和公式支持的情况下表现如何呢，下面给出各自实现的性能表现：

注意：每一行的最后值越大代表性能越好，也就是reward越大。

NVIDIA公司实现的PPO算法的性能表现：

(ppo) devil@OMEN:~/isaacgym/google_brax_ppo_pytorch$
(ppo) devil@OMEN:~/isaacgym/google_brax_ppo_pytorch$
(ppo) devil@OMEN:~/isaacgym/google_brax_ppo_pytorch$
(ppo) devil@OMEN:~/isaacgym/google_brax_ppo_pytorch$ python ppo_nvidia.py

-92.46276 615.6472 619.4814 1598.58 3491.018 4389.2173 4720.664 4956.7036 5157.224 5403.6167 5660.0483
-293.88397 428.9017 683.35486 759.5667 2508.6987 3483.2837 4241.0996 4866.8745 5309.0547 5607.0405 5807.251
-343.99326 541.02106 538.8536 1511.9242 2728.268 3476.1067 4154.212 4556.845 4844.14 5185.3545 5527.5596
-191.4029 666.20013 568.6209 1540.9491 2591.868 3296.225 3961.9253 4730.8076 5330.6 5634.892 5967.589
-311.39725 475.02048 477.9977 1368.197 2588.6013 3490.4133 4133.569 4719.386 5203.3667 5467.0454 5822.964
-63.62652 624.08026 500.64517 1502.9352 2627.319 3303.9001 3867.9912 4238.0215 4681.1646 5099.2637 5538.38
-408.4421 510.3886 498.45285 1081.5658 2229.9773 3054.2632 3537.7908 3872.1826 4265.0864 4656.0996 4997.206
-212.69945 581.74786 713.21924 1095.143 2852.1592 3918.4485 4699.765 5091.0083 5394.695 5612.1733 5851.659
-324.99445 463.03882 515.9956 1046.4734 2209.4084 3184.328 3614.8186 4063.7363 4281.7144 4665.837 5020.642
-276.30496 428.47794 460.0709 857.62274 1759.2151 2813.151 3311.0247 3946.3518 4774.614 5690.9824 6539.924
-306.20178 517.5707 476.00766 1057.7833 2050.8884 2862.6584 3293.738 4310.5254 4921.074 5340.552 5676.209
-299.69257 623.89087 482.17316 1458.4841 2388.513 3250.9512 3694.5715 3775.5378 4847.8716 5599.755 5873.143
-125.3056 654.55273 705.49445 1482.1265 2603.1406 3075.0476 3668.7322 4589.628 5283.5356 5741.815 6166.7705
-285.0059 549.20746 876.36383 1402.4784 2500.9507 3047.863 3459.8203 3703.797 4114.6387 4502.3013 4766.3794
-241.96617 512.50684 555.71185 912.9197 2015.5284 2612.5881 2849.5393 3432.3162 4001.3625 4579.4155 5394.184
-68.229324 453.25262 615.454 1037.2614 2050.4932 2730.044 3150.9194 3691.9043 4222.9795 5046.6445 5490.1016
-287.40823 668.20135 584.20404 1834.8651 2561.1052 3072.583 3335.0125 3985.2122 4359.7812 4571.1724 4551.153
-394.80255 500.0413 408.36472 1182.8118 2502.029 3133.8757 3633.9517 3946.0864 4576.0903 5148.457 5726.9873
-271.14374 496.1476 357.79 917.76013 2121.5967 2780.4185 3230.8884 3570.609 3860.94 4307.6743 4990.6665
-352.497 -18.338879 408.7898 651.40247 627.79315 2473.3062 3442.1694 3934.7588 4397.5635 4772.0923 5221.927

Google公司的PPO算法实现的性能表现：

(ppo) devil@OMEN:~/isaacgym/google_brax_ppo_pytorch$
(ppo) devil@OMEN:~/isaacgym/google_brax_ppo_pytorch$ python ppo_google.py

-151.92789 675.2054 843.941 1671.0323 2254.3054 3109.0151 3578.2156 4327.9575 4922.5435 5312.915 5528.675

-222.82672 608.0872 708.7845 1256.1017 2426.4524 3064.8662 3305.1748 3814.818 4554.5522 5282.8154 5659.039
-194.07735 612.9101 887.85455 1451.6993 2490.8435 3206.251 4362.8076 5255.4697 5905.1665 6497.951 6871.8833
-193.992 575.5923 616.4585 1826.0192 2767.8145 3423.667 3964.7856 4502.3784 4883.922 5245.124 5498.1953
-203.13052 738.5986 935.9803 2012.8353 2726.0715 3160.4214 3391.8105 3638.6821 3938.2808 4264.0386 4769.1836
-186.69662 647.7069 631.8334 1169.1359 2479.4143 3104.97 3466.6614 3906.9832 4365.091 4677.6543 4941.117
-355.6686 584.8635 958.773 1538.586 2527.5776 3121.4744 3555.5793 3789.8745 3944.2214 4143.7837 4565.5293
-113.433624 628.0208 1127.1516 2064.5857 2751.531 3127.0398 3514.5688 3901.7441 4413.523 4819.1406 5247.891
-180.58922 548.8948 710.517 1568.603 2407.2134 2763.0454 3030.4236 3327.0989 3482.7922 3661.5115 3834.1274
-299.12137 590.0653 761.4747 1798.6235 2725.6143 3309.9133 4051.2483 4577.1196 5234.373 5494.769 5713.4204
-304.54407 629.31726 734.1538 1647.8328 2612.3733 3263.9976 3622.268 4141.8755 4711.332 5183.674 5509.048
-198.04155 685.04913 644.2389 1482.0554 2523.795 3091.4492 3477.1665 3695.65 4109.457 4345.8647 4835.086
-279.81683 763.9339 884.2232 1734.2968 2639.7998 3131.6545 3823.177 4479.641 5142.165 5552.4385 5684.3203
-227.01794 575.051 791.56024 1349.687 2421.2747 2967.627 3403.47 3918.3408 4583.2026 5098.737 5415.042
-188.58012 614.0997 601.72015 1463.2482 2654.8445 3279.124 3575.5994 3773.3477 3757.1409 4159.688 4267.0933
-381.04434 556.0338 778.38 1440.889 2346.758 2832.1013 3354.068 4011.1665 4585.723 5066.0977 5489.0034
-238.84843 608.9157 657.5136 1570.1979 2383.2021 2841.463 3231.8225 3569.5278 3804.6384 4278.828 4853.5464
-272.51273 671.35693 718.05566 1686.8368 2702.0715 3344.3562 3754.391 4116.043 4560.265 4979.059 5207.547
-198.75876 538.0805 861.5901 1772.03 2675.996 3229.8008 3636.4485 4043.887 4436.2393 4858.293 5114.886
-322.20215 741.1053 711.51953 1981.2828 2622.7393 3018.7263 3448.417 4047.6506 4599.3955 5183.3896 5554.3145

这里我并没有给出最终的结果的平均和求方差操作，因为在这种比较少的20次重复试验下二者结果在相近的情况下是无法分出谁好谁坏的，因此在有了上面的性能结果对比后我们可以得到下面的几个结论：

1. 在原始PPO论文技术上不严格的按照原始数学形式进行的计算也是有可能做到不影响算法性能的（至少没有明显差异），这在某种层面上也说明当前的AI发展所是在数学基础上构建的，都是也只是做到了借鉴和部分使用数学的程度，这并不是数学学科中的数学公式的推导那样，数学理论在AI领域更多的是用来在一个算法发明后进行一定程度上的解释而很难能够用来推导出AI算法，更难以用来区分哪个AI算法好坏的，或者说目前的AI算法更多的可以被认为是实践派而不是理论派；
2. 虽然很多AI算法在不同的公司、企业、社区、还有各种AI的算法库（library）中实现细节各有不同，甚至有很大差异，并且很多都和原始发表的论文中的原始形式有较大差异，但是这些不同的实现如果被广大的社区、科研领域、企业公司等采用，那么就说明这种差异的实现并没有导致不同实现下的算法在具体表现中有明显的差异，这也可以要一些完美主义者（本人就属于这种）不需要过度的对不同的library中的实现上的一些不同（包括核心过程的不同，也包括一些细节上的trick的不同）过多的计较，因为经验告诉我们这种差异没啥大的性能差异，不过需要注意这些说的这些不同的实现都是经过各大互联网公司和高校科研院所等广泛使用的，而不是你在GitHub上随便找的那种，如果是一个比较陌生的实现方式还是要谨慎的，毕竟这种是真的没经过广泛实践验证的。

PS：

虽然各大公司和library的具体实现的不同并不会造成算法具体表现的明显差异，但是我个人还是偏向于使用那种更贴近于原始论文实现的那种实现，因为这样更好理解。

个人github博客地址：
https://devilmaycry812839668.github.io/

在
Streamlit
中，布局类组件扮演着至关重要的角色。

它们不仅决定了应用程序的视觉呈现和用户体验，也极大地增强了页面内容的组织性和可读性。

通过这些组件，开发者可以灵活地划分页面空间，创建出清晰、有条理的布局结构。

本篇主要介绍
3种
构建
Streamlit App
时常用的3种布局类组件：

• st.container
  ：用于封装和组合多个组件，形成统一的视觉单元
• st.columns
  ：将内容以并列的方式展示，提高信息展示的效率和效果
• st.expander
  ：提供了可折叠的面板功能，使得额外信息可以在需要时展开查看，既节省了空间又保持了界面的整洁性

1. st.container

st.container
通过将多个组件放入一个容器中，可以轻松地控制这些组件的布局和样式。

st.container
本身并不直接提供布局参数，一般是通过
with
语句将要包含的组件放入容器中，

或者，通过嵌套使用其他布局组件（如
st.column
和
st.row
等）来在容器内部实现更复杂的布局。

1.1. 使用示例

假定这样一个场景，在一个数据分析应用中，需要同时展示数据表格和相关的文字说明。

import streamlit as st
import pandas as pd

# 创建示例数据
data = pd.DataFrame(
    {
        "A": [1, 2, 3],
        "B": [4, 5, 6],
        "C": [7, 8, 9],
    }
)

# 使用st.container封装数据表格和说明文字
with st.container():
    st.dataframe(data)
    st.markdown("这是数据表格的说明，提供了对数据的简要描述和分析。")

或者在一个机器学习模型演示应用中，需要同时展示模型预测结果和交互式控件（如滑块），

也可以通过
st.container
，将预测结果和滑块控件组合在一起，形成一个交互式的界面

# 创建一个滑块控件
slider_value = st.slider("调整滑块以查看不同结果", 0, 100)

# 使用st.container封装预测结果和滑块控件
with st.container():
    st.write(f"当前滑块值为：{slider_value}")
    st.write("这是一个简单的机器学习模型演示。通过调整滑块，你可以看到不同的预测结果。")

2. st.columns

st.columns
组件用于创建一个列布局的容器，它可以将页面内容分割成多个垂直排列的列。

当需要在页面上同时展示多个并列的组件或信息块时，可以考虑使用
st.columns
。

st.columns
参数很简单，它使用一个整数作为参数，该整数指定要创建的列数。

2.1. 使用示例

首先，模拟一个数据可视化应用中，需要并列展示一个折线图和相关的文字说明的场景。

import streamlit as st
import pandas as pd
import matplotlib.pyplot as plt

# 创建示例数据
data = pd.DataFrame(
    {
        "X": [1, 2, 3, 4, 5],
        "Y": [10, 15, 13, 17, 16],
    }
)

# 绘制折线图
plt.plot(data["X"], data["Y"])
plt.xlabel("X-Axis")
plt.ylabel("Y-Axis")
plt.title("chart example")

# 使用st.columns并列展示图表和文字说明
col1, col2 = st.columns(2)
col1.pyplot(plt)
col2.write("这是一个折线图示例，展示了X轴和Y轴之间的关系。")

再模拟一个数据对比的应用，需要同时展示多个数据表格以便进行比较和分析。

# 创建示例数据
data1 = pd.DataFrame({"A": [1, 2, 3], "B": [4, 5, 6]})

data2 = pd.DataFrame({"A": [7, 8, 9], "B": [10, 11, 12]})

# 使用st.columns创建三列布局展示数据表格
col1, col2, col3 = st.columns(3)
col1.dataframe(data1)
col2.dataframe(data2)
col3.write("这是两个数据表格的对比展示。通过并列展示，你可以更方便地进行比较和分析。")

3. st.expander

st.expander
组件用于创建一个可折叠的面板，允许用户点击以展开或隐藏面板内的内容。

当需要在页面上提供额外的信息或选项，但又不希望这些信息始终可见时，可以考虑使用
st.expander
。

st.expander
将一个字符串作为参数，该字符串将作为面板的标题显示。

然后，可以在
with
语句块内添加要在面板中显示的组件。

3.1. 使用示例

首先模拟一个数据分析的应用，其中包含一个详细设置的面板，但默认情况下这些设置是隐藏的。

import streamlit as st

# 创建一个包含详细设置的st.expander面板
with st.expander("详细设置"):
    st.write("这里是一些详细的设置选项，如数据过滤、排序等。")
    st.slider("数据过滤阈值", 0, 100)
    st.checkbox("启用排序功能")

# 主界面内容模拟
st.write("这是一个数据分析应用的主界面。你可以点击上面的“详细设置”来查看和修改设置。")

此外，在一个比较复杂的Web应用中，如果需要提供一个包含帮助文档和指南的面板，以便用户在使用时参考。

那么，可以使用
st.expander
，将帮助文档和指南隐藏在一个可折叠的面板中，

用户可以在需要时查看这些信息，而不会影响主界面的展示效果。

with st.expander("帮助文档和指南"):
    st.markdown(
        """
    # 帮助文档和指南

    欢迎使用本应用！这里是一些常用的操作和技巧，帮助你更好地使用本应用。

    - **如何开始**：点击左侧导航栏中的“开始”按钮，进入应用主界面。
    - **数据导入**：在主界面上方点击“导入数据”按钮，上传你的数据文件。
    - **数据分析**：在数据导入后，点击“分析数据”按钮，选择你想要进行的分析类型。

    如有任何疑问，请联系技术支持。
    """
    )

# 主界面模拟
st.write("这是一个复杂的Web应用。如果你需要帮助或指南，请点击上面的“帮助文档和指南”。")

4. 总结

这
3个组件
在布局时的侧重点不同，其中，
st.container
侧重组件封装，
st.columns
侧重列布局，而
st.expander
侧重信息隐藏。

我们在使用时根据应用的具体展现形式来选择，

比如，需要组织复杂布局时则用
st.container
，需要并列展示信息时用
st.columns
，需要隐藏额外信息时用
st.expander
。

1.概述

cornerstone中核心即为raft_server的实现。
在raft里面有follower，leader，candidate三种角色，且角色身份还可以相互切换。
写三个类follower，leader，candidate显得没必要，因为三个类可以共享许多成员变量，如term，log_store等等。因此在cornerstone中抽象出raft_server这一个类，而raft_server的角色可以在三种状态相互切换。
下图为cornerstone中关于管理三种角色的示意图。

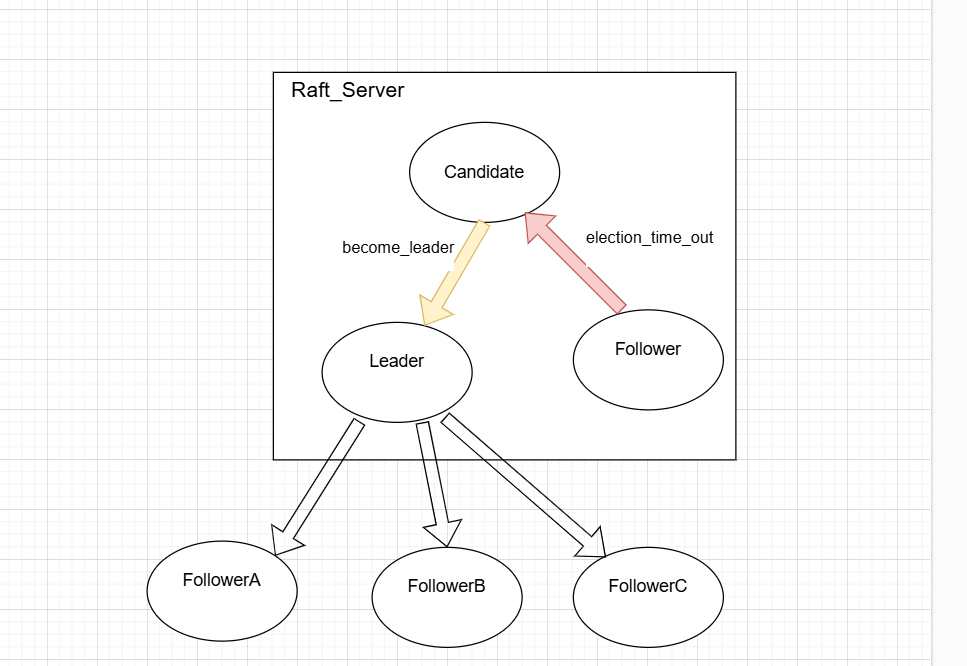
在本文中我们先解析单个raft_server节点中角色变化的过程，再关注leader与follower的通信。

2. raft_server节点中角色变化

2.1.1 逻辑概览

示意图如下

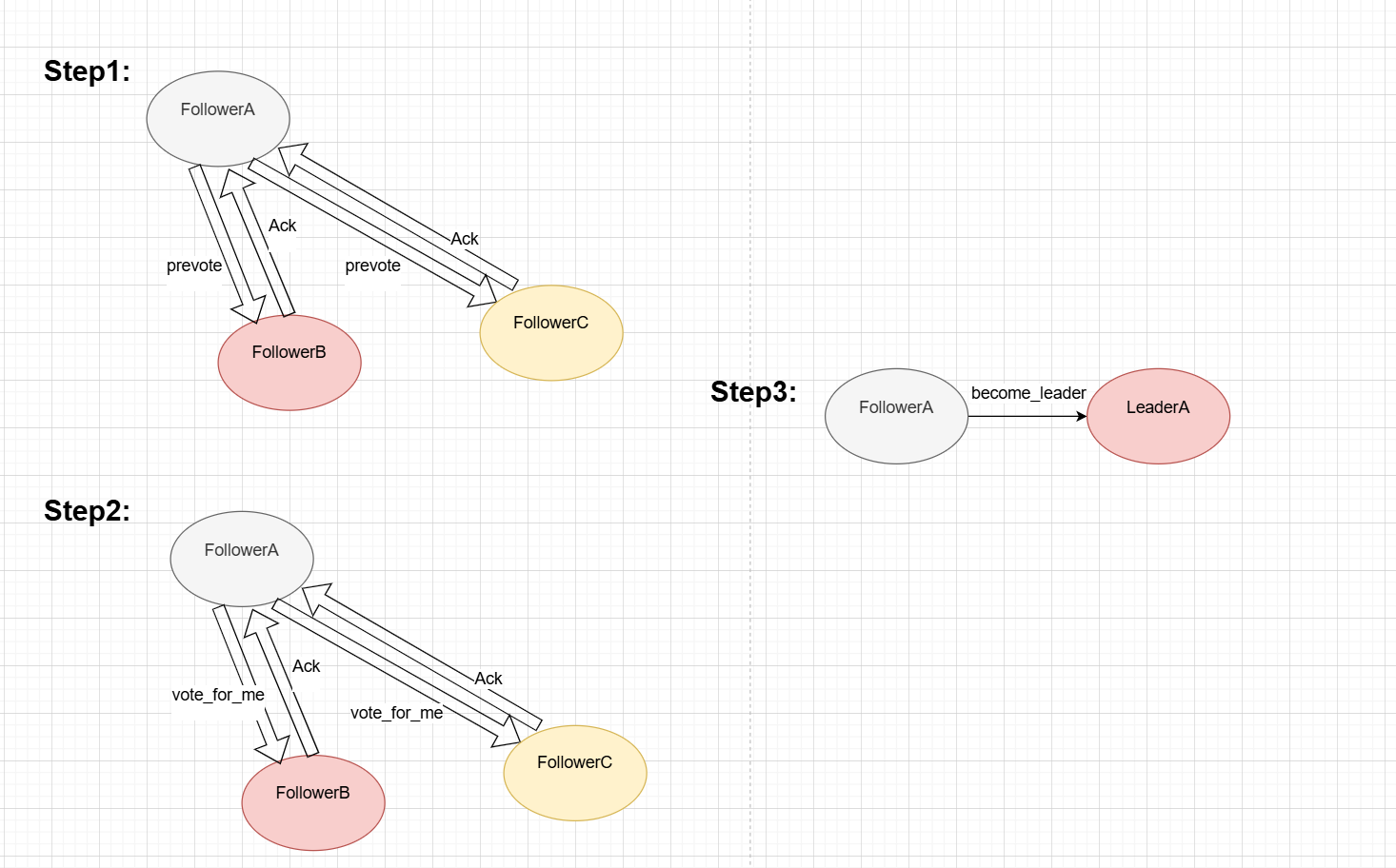
• 1.当election_timeout事件发生后，followerA便按照上图的顺序先向自己的peer-follower发送prevote，得到半数以上的同意后开始下一步。
• 2.followerA通过prevote知道自己网络状态良好，成为candidate，然后发送正式的request_vote请求，得到半数以上的同意后开始下一步。
• 3.followerA调用become_leader，成为leader

2.1.2 election_timeout代码解析：

void raft_server::handle_election_timeout()
{
    recur_lock(lock_);
    if (steps_to_down_ > 0)
    {
        if (--steps_to_down_ == 0)
        {
            l_->info("no hearing further news from leader, remove this server from cluster and step down");
            for (std::list<ptr<srv_config>>::iterator it = config_->get_servers().begin();
                 it != config_->get_servers().end();
                 ++it)
            {
                if ((*it)->get_id() == id_)
                {
                    config_->get_servers().erase(it);
                    ctx_->state_mgr_->save_config(*config_);
                    break;
                }
            }

            ctx_->state_mgr_->system_exit(-1);
            return;
        }

        l_->info(sstrfmt("stepping down (cycles left: %d), skip this election timeout event").fmt(steps_to_down_));
        restart_election_timer();
        return;
    }

    if (catching_up_)
    {
        // this is a new server for the cluster, will not send out vote req until conf that includes this srv is
        // committed
        l_->info("election timeout while joining the cluster, ignore it.");
        restart_election_timer();
        return;
    }

    if (role_ == srv_role::leader)
    {
        l_->err("A leader should never encounter election timeout, illegal application state, stop the application");
        ctx_->state_mgr_->system_exit(-1);
        return;
    }

    if (ctx_->params_->prevote_enabled_ && role_ == srv_role::follower)
    {
        if (prevote_state_ && !prevote_state_->empty())
        {
            l_->debug("Election timeout, but there is already a prevote ongoing, ignore this event");
        }
        else
        {
            l_->debug("Election timeout, start prevoting");
            request_prevote();
        }
    }
    else
    {
        l_->debug("Election timeout, change to Candidate");
        become_candidate();
    }
}

• 1.首先steps_to_down_--，判断steps_to_down_是否减为0了，为0则继续下一步，不为0则不处理，重置election_timer。
• 2.判断是不是新加入的server在catching-up集群的log_entry及相应配置信息，是则不处理，重置election_timer，否则继续下一步。
• 3.判断进行了prevote没有，进行了就become_candidate，否则就去prevote。

知识点：
采用step_down机制，给server可能因偶然网络故障一次缓冲的机会，初始化step_down为2，先给step_down--，如果是偶然故障减为1依然还有1次机会。

2.1.3 request_prevote源码解析

void raft_server::request_prevote()
{
    l_->info(sstrfmt("prevote started with term %llu").fmt(state_->get_term()));
    bool change_to_candidate(false);
    {
        read_lock(peers_lock_);
        if (peers_.size() == 0)
        {
            change_to_candidate = true;
        }
    }

    if (change_to_candidate)
    {
        l_->info("prevote done, change to candidate and start voting");
        become_candidate();
        return;
    }

    if (!prevote_state_)
    {
        prevote_state_ = std::make_unique<prevote_state>();
    }

    prevote_state_->inc_accepted_votes();
    prevote_state_->add_voted_server(id_);
    {
        read_lock(peers_lock_);
        for (peer_itor it = peers_.begin(); it != peers_.end(); ++it)
        {
            ptr<req_msg> req(cs_new<req_msg>(
                state_->get_term(),
                msg_type::prevote_request,
                id_,
                it->second->get_id(),
                term_for_log(log_store_->next_slot() - 1),
                log_store_->next_slot() - 1,
                quick_commit_idx_));
            l_->debug(sstrfmt("send %s to server %d with term %llu")
                          .fmt(__msg_type_str[req->get_type()], it->second->get_id(), state_->get_term()));
            it->second->send_req(req, ex_resp_handler_);
        }
    }
}

• 1.特判peer的大小是否为0，为0直接跳过prevote与vote阶段，直接become_candidate，否则继续。
• 2.遍历每一个peer，向peer发送req_msg，类型为msg_type::prevote_request，req_msg里面包含自身的log_store中entry的last_idx，last_term，commit_idx情况给peer决定是否投票。

知识点：
为什么peer的大小为0就直接become_candidate而不是报持follower状态呢？

2.1.4 request_vote源码解析

void raft_server::request_vote()
{
    l_->info(sstrfmt("requestVote started with term %llu").fmt(state_->get_term()));
    state_->set_voted_for(id_);
    ctx_->state_mgr_->save_state(*state_);
    votes_granted_ += 1;
    voted_servers_.insert(id_);

    bool change_to_leader(false);
    {
        read_lock(peers_lock_);

        // is this the only server?
        if (votes_granted_ > (int32)(peers_.size() + 1) / 2)
        {
            election_completed_ = true;
            change_to_leader = true;
        }
        else
        {
            for (peer_itor it = peers_.begin(); it != peers_.end(); ++it)
            {
                ptr<req_msg> req(cs_new<req_msg>(
                    state_->get_term(),
                    msg_type::vote_request,
                    id_,
                    it->second->get_id(),
                    term_for_log(log_store_->next_slot() - 1),
                    log_store_->next_slot() - 1,
                    quick_commit_idx_));
                l_->debug(sstrfmt("send %s to server %d with term %llu")
                              .fmt(__msg_type_str[req->get_type()], it->second->get_id(), state_->get_term()));
                it->second->send_req(req, resp_handler_);
            }
        }
    }

    if (change_to_leader)
    {
        become_leader();
    }
}

• 整体与prevote类似，关键点在于计算是否有一半以上的节点支持的技巧：
  if (votes_granted_ > (int32)(peers_.size() + 1) / 2)
  。不管奇数还是偶数，一半以上都是⌊(x + 1) / 2⌋。

2.1.5 become_leader源码解析

void raft_server::become_leader()
{
    stop_election_timer();
    role_ = srv_role::leader;
    leader_ = id_;
    srv_to_join_.reset();
    ptr<snapshot> nil_snp;
    {
        read_lock(peers_lock_);
        for (peer_itor it = peers_.begin(); it != peers_.end(); ++it)
        {
            it->second->set_next_log_idx(log_store_->next_slot());
            it->second->set_snapshot_in_sync(nil_snp);
            it->second->set_free();
            enable_hb_for_peer(*(it->second));
        }
    }

    if (config_->get_log_idx() == 0)
    {
        config_->set_log_idx(log_store_->next_slot());
        bufptr conf_buf = config_->serialize();
        ptr<log_entry> entry(cs_new<log_entry>(state_->get_term(), std::move(conf_buf), log_val_type::conf));
        log_store_->append(entry);
        l_->info("save initial config to log store");
        config_changing_ = true;
    }

    if (ctx_->event_listener_)
    {
        ctx_->event_listener_->on_event(raft_event::become_leader);
    }

    request_append_entries();
}

• 1.把election_timer给停了，同时更新自身的role等属性。
• 2.清空每一个peer原有leader的信息，同时给每个peer设置hb来宣示自己主权。
• 3.如果config_为空，更新config_

知识点：
这里的election_timeout事件其实不发生在election里面，而是在正常任期内发生的，用于触发election。follower在给定时间内没收到leader消息那么就启动vote，就是通过election_timer来实现的，如果收到了leader消息就restart_election_timer继续定时。

3.leader向follower发送消息

3.1 request_append_entries源码解析

void raft_server::request_append_entries()
{
    read_lock(peers_lock_);
    if (peers_.size() == 0)
    {
        commit(log_store_->next_slot() - 1);
        return;
    }

    for (peer_itor it = peers_.begin(); it != peers_.end(); ++it)
    {
        request_append_entries(*it->second);
    }
}

bool raft_server::request_append_entries(peer& p)
{
    if (p.make_busy())
    {
        ptr<req_msg> msg = create_append_entries_req(p);
        p.send_req(msg, resp_handler_);
        return true;
    }

    l_->debug(sstrfmt("Server %d is busy, skip the request").fmt(p.get_id()));
    return false;
}
ptr<req_msg> raft_server::create_append_entries_req(peer& p)
{
    ulong cur_nxt_idx(0L);
    ulong commit_idx(0L);
    ulong last_log_idx(0L);
    ulong term(0L);
    ulong starting_idx(1L);

    {
        recur_lock(lock_);
        starting_idx = log_store_->start_index();
        cur_nxt_idx = log_store_->next_slot();
        commit_idx = quick_commit_idx_;
        term = state_->get_term();
    }

    {
        std::lock_guard<std::mutex> guard(p.get_lock());
        if (p.get_next_log_idx() == 0L)
        {
            p.set_next_log_idx(cur_nxt_idx);
        }

        last_log_idx = p.get_next_log_idx() - 1;
    }

    if (last_log_idx >= cur_nxt_idx)
    {
        l_->err(
            sstrfmt("Peer's lastLogIndex is too large %llu v.s. %llu, server exits").fmt(last_log_idx, cur_nxt_idx));
        ctx_->state_mgr_->system_exit(-1);
        return ptr<req_msg>();
    }

    // for syncing the snapshots, for starting_idx - 1, we can check with last snapshot
    if (last_log_idx > 0 && last_log_idx < starting_idx - 1)
    {
        return create_sync_snapshot_req(p, last_log_idx, term, commit_idx);
    }

    ulong last_log_term = term_for_log(last_log_idx);
    ulong end_idx = std::min(cur_nxt_idx, last_log_idx + 1 + ctx_->params_->max_append_size_);
    ptr<std::vector<ptr<log_entry>>> log_entries(
        (last_log_idx + 1) >= cur_nxt_idx ? ptr<std::vector<ptr<log_entry>>>()
                                          : log_store_->log_entries(last_log_idx + 1, end_idx));
    l_->debug(
        lstrfmt("An AppendEntries Request for %d with LastLogIndex=%llu, LastLogTerm=%llu, EntriesLength=%d, "
                "CommitIndex=%llu and Term=%llu")
            .fmt(p.get_id(), last_log_idx, last_log_term, log_entries ? log_entries->size() : 0, commit_idx, term));
    ptr<req_msg> req(cs_new<req_msg>(
        term, msg_type::append_entries_request, id_, p.get_id(), last_log_term, last_log_idx, commit_idx));
    std::vector<ptr<log_entry>>& v = req->log_entries();
    if (log_entries)
    {
        v.insert(v.end(), log_entries->begin(), log_entries->end());
    }

    return req;
}

• 1.cornerstone无处不体现封装隔离的思想，将append-entry向所有peer的请求的实现下放到更小粒度的针对单个peer的append-entry，而即使是针对单个peer的append-entry，依然把底层的发送请求与对peer的状态管理分隔开来。
• 2.create_append_entries_req才是底层的发送请求，这里要分三种情况讨论
  (1).follower的last_log_idx >= leader的cur_nxt_idx，说明follower
  (2).last_log_idx > 0 && last_log_idx < starting_idx - 1，说明follower的log_store差太多，直接给follower安装snapshot而不是按传统发送leader的log_store。
  (3).最后一种情况说明follower与leader的log_store有重合，选出非重合的log_store发送给follower。

知识点：
follower的日志落后很多的时候，可以直接发送snapshot加快同步速度。

3.2 create_sync_snapshot_req源码解析

ptr<req_msg> raft_server::create_sync_snapshot_req(peer& p, ulong last_log_idx, ulong term, ulong commit_idx)
{
    std::lock_guard<std::mutex> guard(p.get_lock());
    ptr<snapshot_sync_ctx> sync_ctx = p.get_snapshot_sync_ctx();
    ptr<snapshot> snp;
    if (sync_ctx != nilptr)
    {
        snp = sync_ctx->get_snapshot();
    }

    if (!snp || (last_snapshot_ && last_snapshot_->get_last_log_idx() > snp->get_last_log_idx()))
    {
        snp = last_snapshot_;
        if (snp == nilptr || last_log_idx > snp->get_last_log_idx())
        {
            l_->err(lstrfmt("system is running into fatal errors, failed to find a snapshot for peer %d(snapshot null: "
                            "%d, snapshot doesn't contais lastLogIndex: %d")
                        .fmt(p.get_id(), snp == nilptr ? 1 : 0, last_log_idx > snp->get_last_log_idx() ? 1 : 0));
            ctx_->state_mgr_->system_exit(-1);
            return ptr<req_msg>();
        }

        if (snp->size() < 1L)
        {
            l_->err("invalid snapshot, this usually means a bug from state machine implementation, stop the system to "
                    "prevent further errors");
            ctx_->state_mgr_->system_exit(-1);
            return ptr<req_msg>();
        }

        l_->info(sstrfmt("trying to sync snapshot with last index %llu to peer %d")
                     .fmt(snp->get_last_log_idx(), p.get_id()));
        p.set_snapshot_in_sync(snp);
    }

    ulong offset = p.get_snapshot_sync_ctx()->get_offset();
    int32 sz_left = (int32)(snp->size() - offset);
    int32 blk_sz = get_snapshot_sync_block_size();
    bufptr data = buffer::alloc((size_t)(std::min(blk_sz, sz_left)));
    int32 sz_rd = state_machine_->read_snapshot_data(*snp, offset, *data);
    if ((size_t)sz_rd < data->size())
    {
        l_->err(
            lstrfmt(
                "only %d bytes could be read from snapshot while %d bytes are expected, must be something wrong, exit.")
                .fmt(sz_rd, data->size()));
        ctx_->state_mgr_->system_exit(-1);
        return ptr<req_msg>();
    }

    bool done = (offset + (ulong)data->size()) >= snp->size();
    std::unique_ptr<snapshot_sync_req> sync_req(new snapshot_sync_req(snp, offset, std::move(data), done));
    ptr<req_msg> req(cs_new<req_msg>(
        term,
        msg_type::install_snapshot_request,
        id_,
        p.get_id(),
        snp->get_last_log_term(),
        snp->get_last_log_idx(),
        commit_idx));
    req->log_entries().push_back(cs_new<log_entry>(term, sync_req->serialize(), log_val_type::snp_sync_req));
    return req;
}

• 1.首先获取旧的snapshot，判断是否能更新，能的话就更新。
• 2.把snapshot绑定到peer身上，因为snapshot挺大，需要分段发，所以要绑定到peer身上。
• 3.offset记录snapshot发送到哪里了，bool done就是记录是否发送完了snapshot。
• 4.发送snapshot_req。

知识点：
即使使用了offset记录发送的偏移，但是根据这里的代码很明显只发送了一次，那怎么能做到分段发送呢？
答案在cornerstone对于resp的处理里面，因为客户端接受snapshot，安装snapshot需要一定时间。不可能leader发送完一段snapshot紧跟着又发送下一段，leader需要等待follower处理完当前一段snapshot发送ack过来后再发送下一段，收到follower的resp后leader会再次调用这个函数，实现分段发送。

4.集群cluster的变更

4.1 cluster添加server

ptr<async_result<bool>> raft_server::add_srv(const srv_config& srv)
{
    bufptr buf(srv.serialize());
    ptr<log_entry> log(cs_new<log_entry>(0, std::move(buf), log_val_type::cluster_server));
    ptr<req_msg> req(cs_new<req_msg>((ulong)0, msg_type::add_server_request, 0, 0, (ulong)0, (ulong)0, (ulong)0));
    req->log_entries().push_back(log);
    return send_msg_to_leader(req);
}

ptr<async_result<bool>> raft_server::send_msg_to_leader(ptr<req_msg>& req)
{
    typedef std::unordered_map<int32, ptr<rpc_client>>::const_iterator rpc_client_itor;
    int32 leader_id = leader_;
    ptr<cluster_config> cluster = config_;
    bool result(false);
    if (leader_id == -1)
    {
        return cs_new<async_result<bool>>(result);
    }

    if (leader_id == id_)
    {
        ptr<resp_msg> resp = process_req(*req);
        result = resp->get_accepted();
        return cs_new<async_result<bool>>(result);
    }

    ptr<rpc_client> rpc_cli;
    {
        auto_lock(rpc_clients_lock_);
        rpc_client_itor itor = rpc_clients_.find(leader_id);
        if (itor == rpc_clients_.end())
        {
            ptr<srv_config> srv_conf = config_->get_server(leader_id);
            if (!srv_conf)
            {
                return cs_new<async_result<bool>>(result);
            }

            rpc_cli = ctx_->rpc_cli_factory_->create_client(srv_conf->get_endpoint());
            rpc_clients_.insert(std::make_pair(leader_id, rpc_cli));
        }
        else
        {
            rpc_cli = itor->second;
        }
    }

    if (!rpc_cli)
    {
        return cs_new<async_result<bool>>(result);
    }

    ptr<async_result<bool>> presult(cs_new<async_result<bool>>());
    rpc_handler handler = [presult](ptr<resp_msg>& resp, const ptr<rpc_exception>& err) -> void
    {
        bool rpc_success(false);
        ptr<std::exception> perr;
        if (err)
        {
            perr = err;
        }
        else
        {
            rpc_success = resp && resp->get_accepted();
        }

        presult->set_result(rpc_success, perr);
    };
    rpc_cli->send(req, handler);
    return presult;
}

• add_srv先生成一个req，把变更的srv信息存到req附带的log里面。由于不是用于follower与leader之间的log_store同步，所以原来的last_log_idx，last_log_term，commit_idx全部为0。
• 调用send_msg_to_leader向leader发送变更srv的信息

4.2 cluster移除server

ptr<async_result<bool>> raft_server::remove_srv(const int srv_id)
{
    bufptr buf(buffer::alloc(sz_int));
    buf->put(srv_id);
    buf->pos(0);
    ptr<log_entry> log(cs_new<log_entry>(0, std::move(buf), log_val_type::cluster_server));
    ptr<req_msg> req(cs_new<req_msg>((ulong)0, msg_type::remove_server_request, 0, 0, (ulong)0, (ulong)0, (ulong)0));
    req->log_entries().push_back(log);
    return send_msg_to_leader(req);
}

• 同add_srv的分析。

5.总结

• 1.合理架构raft中各角色关系，采用一个server外加peers的组合，server内部可follower，candidate，leader相互转换。
• 2.采用step_down机制，给server可能因偶然网络故障一次缓冲的机会。
• 3.计算是否有一半以上的节点支持的技巧：if (votes_granted_ > (int32)(peers_.size() + 1) / 2)。不管奇数还是偶数，一半以上都是⌊(x + 1) / 2⌋。
• 4.follower的日志落后很多的时候，可以直接发送snapshot加快同步速度。
• 5.发送大文件采用offset机制分段传送。