线段树知识乱讲
前言
算法竞赛题目考察的是选手对于数据结构的选取与算法的巧妙结合,而数据结构中线段树扮演一个至关重要的角色,而近期(CSP 结束)在 hfu 的安排下我们需要自己弄一周的 ds,所以就有了这篇奇妙的博客。
线段树基础知识
在我看来,线段树其实就是在数组的基础上添加了一些
额外
的点,这些点用于维护原数组的信息,在此基础上又添加一些点维护
之前添加的点
的信息,就这么一层一层往上直到最后只有一个点,而这个点也就管理了这整个数组。而这些点之间的管理关系也就形成了一棵树,故为线段树。
然后考虑添加的这些点,如果这些点很随意,最劣情况可能会被卡成一些神秘的东西,于是我们就让第一层维护两个点,第二层维护四个点,这样我们只会建出
\(\log\)
层,并且增加的节点数是
\(O(n)\)
的。这样线段树就有了很优美的性质,也称得上真正的线段树了。
对于用线段树维护信息,我们不必在每次修改操作将相关的节点全部修改,但是我们需要知道我们应该去修改哪些地方。比如我在树上走,走到了一个区间
\([l,r]\)
,如果这个区间被修改的区间包含,这就意味着我需要将这整个区间修改,可是直接修改是
\(O(len)\)
的,这时我们就可以先将这个地方的修改记下来,等到我查询这个区间的时候在处理它。这样在线段树上找出的区间是
\(O(\log)\)
的,所以正常的修改就是找区间加上
\(O(1)\)
打标记。
而查询和修改同理,都是在树上走每次碰到一个区间能够被全部算进贡献就直接加入贡献,否则就继续往下走,但是在修改和查询时都需要注意下放之前的标记,也就是我
下一次
走到有标记的节点时我会对其进行一些操作,这时原来的标记与现在的操作的两个区间大概率是不同的,所以在操作前我们需要下放之前的标记。
然后放两道板子。
我们可以将线段树给建出,过程就是一个遍历树的过程,只是到树叶(也就是原数组)时需要保存信息再一层一层传回去。修改与查询在此不再赘述。
void upd(int x){
s[x] = s[ls] + s[rs];
}
void bld(int x, int l, int r){
if(l == r)return (void)(s[x] = a[l]);
int mid = l + r >> 1;
bld(ls, l, mid), bld(rs, mid + 1, r);
upd(x);
}
void pd(int x, int l, int r){
if(! tg[x])return; int mid = l + r >> 1;
tg[ls] += tg[x], tg[rs] += tg[x];
s[ls] += tg[x] * (mid - l + 1);
s[rs] += tg[x] * (r - mid);
return (void)(tg[x] = 0);
}
void mdf(int x, int l, int r, int ql, int qr, ll y){
if(ql <= l and r <= qr)return (void)(s[x] += y * (r - l + 1), tg[x] += y);
int mid = l + r >> 1; pd(x, l, r);
if(ql <= mid)mdf(ls, l, mid, ql, qr, y);
if(mid < qr)mdf(rs, mid + 1, r, ql, qr, y);
upd(x);
}
ll qry(int x, int l, int r, int ql, int qr){
if(ql <= l and r <= qr)return s[x];
int mid = l + r >> 1; ll res = 0; pd(x, l, r);
if(ql <= mid)res = qry(ls, l, mid, ql, qr);
if(mid < qr)res += qry(rs, mid + 1, r, ql, qr);
return res;
}
这时有了乘法操作修改与下放似乎变得复杂,这时我们需要先分析不同操作的优先级。
首先我们肯定对于乘法与加法分别打标记,然后对于一个加法标记,它的意义是让区间加上一个数,如果直接加那么乘法标记就会受影响。将乘法标记增加一定是错的,所以我们应该将它下放。注意到乘法的优先级是高于加法,所以在下放时要让乘法标记先下放。
如果是有一个乘法标记,这时之前区间内的加法标记也应该乘上它,因为乘法分配律。所以乘法就直接全改了就行。
void upd(int x){
s[x] = (s[ls] + s[rs]) % p;
}
void bld(int x, int l, int r){
tg2[x] = 1;
if(l == r)return (void)(s[x] = a[l]);
int mid = l + r >> 1;
bld(ls, l, mid), bld(rs, mid + 1, r);
upd(x);
}
void pd(int x, int l, int r){
int mid = l + r >> 1;
tg1[ls] = (tg1[ls] * tg2[x] + tg1[x]) % p, tg1[rs] = (tg1[rs] * tg2[x] + tg1[x]) % p;
s[ls] = (s[ls] * tg2[x] + tg1[x] * (mid - l + 1)) % p;
s[rs] = (s[rs] * tg2[x] + tg1[x] * (r - mid)) % p;
tg2[ls] = tg2[ls] * tg2[x] % p;
tg2[rs] = tg2[rs] * tg2[x] % p;
return (void)(tg1[x] = 0, tg2[x] = 1);
}
void mdf1(int x, int l, int r, int ql, int qr, ll y){
if(ql <= l and r <= qr)return (void)(s[x] = y * s[x] % p, tg2[x] = tg2[x] * y % p, tg1[x] = tg1[x] * y % p);
int mid = l + r >> 1; pd(x, l, r);
if(ql <= mid)mdf1(ls, l, mid, ql, qr, y);
if(mid < qr)mdf1(rs, mid + 1, r, ql, qr, y);
upd(x);
}
void mdf2(int x, int l, int r, int ql, int qr, ll y){
if(ql <= l and r <= qr)return (void)(s[x] = (s[x] + y * (r - l + 1)) % p, tg1[x] = (tg1[x] + y) % p);
int mid = l + r >> 1; pd(x, l, r);
if(ql <= mid)mdf2(ls, l, mid, ql, qr, y);
if(mid < qr)mdf2(rs, mid + 1, r, ql, qr, y);
upd(x);
}
ll qry(int x, int l, int r, int ql, int qr){
if(ql <= l and r <= qr)return s[x];
int mid = l + r >> 1; ll res = 0; pd(x, l, r);
if(ql <= mid)res = qry(ls, l, mid, ql, qr);
if(mid < qr)res += qry(rs, mid + 1, r, ql, qr);
return res % p;
}
这个题注意修改操作优先级大于加法操作,每次修改操作时需要清空标记。然后就是
不要在叶子节点
\(\text {pushdown}\)
!
void upd(int x){
c[x] = max(c[ls], c[rs]);
}
void build(int x, int l, int r){
tg1[x] = max0810;
if(l == r)return(void)(c[x] = a[l]);
int mid = l + r >> 1;
build(ls, l, mid); build(rs, mid + 1, r);
upd(x);
}
void pdtg1(int x){
if(tg1[x] == max0810)return;
tg2[ls] = tg2[rs] = 0;
c[ls] = c[rs] = tg1[ls] = tg1[rs] = tg1[x];
tg1[x] = max0810;
}
void pd(int x){
pdtg1(x);
if(! tg2[x])return;
c[ls] += tg2[x]; c[rs] += tg2[x];
tg2[ls] += tg2[x]; tg2[rs] += tg2[x];
tg2[x] = 0;
}
void mdfy(int x, int l, int r, int L, int R, int op, ll y){
if(L <= l and r <= R){
if(op ^ 1){
c[x] += y; tg2[x] += y;
}
else{
c[x] = tg1[x] = y;
tg2[x] = 0;
}
return;
}
int mid = l + r >> 1; pd(x);
if(L <= mid)mdfy(ls, l, mid, L, R, op, y);
if(R > mid)mdfy(rs, mid + 1, r, L, R, op, y);
upd(x);
}
ll qry(int x, int l, int r, int L, int R){
if(L <= l and r <= R)return c[x];
int mid = l + r >> 1; ll res = max0810; pd(x);
if(L <= mid)res = qry(ls, l, mid, L, R);
if(R > mid) res = max(res, qry(rs, mid + 1, r, L, R));
return res;
}
P4513 小白逛公园
3倍经验见
这篇
(是的还是我)
线段树维护区间最大子段和的板子题,支持单点修改。
考虑上传答案的过程中需要维护的信息,首先有区间最大子段和
废话
,然后我们合并子区间时有可能从
左边区间的后缀最大加上右边区间的前缀最大
转移答案,所以还要记这两个东西。然后更新前后缀时似乎又需要记一个区间和,不然没法转(读者可自行思考)。然后查询时就同时记录这几个信息。单点修改就直接二分改了就行。
struct node{
ll s, lm, rm, sum;
}sgt[N << 2];
void upd(node &x, node y, node z){
x.sum = y.sum + z.sum;
x.s = max(y.s, max(z.s, y.rm + z.lm));
x.lm = max(y.lm, y.sum + z.lm), x.rm = max(z.rm, z.sum + y.rm);
}
void bld(int x, int l, int r){
if(l == r)return(void)(sgt[x] = {a[l], a[l], a[l], a[l]});
int mid = l + r >> 1;
bld(ls, l, mid), bld(rs, mid + 1, r);
upd(sgt[x], sgt[ls], sgt[rs]);
}
void mdf(int x, int l, int r, int pos, int y){
if(l == r)return(void)(sgt[x] = {y, y, y, y});
int mid = l + r >> 1;
if(pos <= mid)mdf(ls, l, mid, pos, y);
else mdf(rs, mid + 1, r, pos, y);
upd(sgt[x], sgt[ls], sgt[rs]);
}
node qry(int x, int l, int r, int ql, int qr){
if(ql <= l and r <= qr)return sgt[x];
int mid = l + r >> 1; node res, res1, res2; bool o1(false), o2(false);
if(ql <= mid)res1 = qry(ls, l, mid, ql, qr), o1 = true;
if(mid < qr)res2 = qry(rs, mid + 1, r, ql, qr), o2 = true;
if(! o1 or ! o2)res = o1 ? res1 : res2;
else upd(res, res1, res2);
return res;
}
P11071 「QMSOI R1」 Distorted Fate
首先拆位。观察式子,里面有一个按位或,说明了什么?说明如果
\(a_i\)
中出现了一那么后面的就都有值了,所以我们的任务就是每次找到区间内最左边的一然后答案就是从第一个一开始到右端点的长度。
但是看到空间限制你会发现这题有点抽象,所以你拆位后只能共用一棵线段树了。然后就是线段树维护的是区间是否有 0/1、以及每次异或后可能存在的懒标记这三者都可以用
bool
类型的数组维护。
但是这只是离线的,
因为不会在线所以自己去看吧
。
struct qarray{
int op, l, r, x; ll ans;
}q[N];
bool b[N], s0[N << 2], s1[N << 2], tg[N << 2];
#define ls x << 1
#define rs x << 1 | 1
void upd(int x){
s0[x] = s0[ls] | s0[rs];
s1[x] = s1[ls] | s1[rs];
}
void build(int x, int l, int r){
tg[x] = 0;
if(l == r)return(void)(s0[x] = b[l] ^ 1, s1[x] = b[l]);
int mid = l + r >> 1;
build(ls, l, mid), build(rs, mid + 1, r);
upd(x);
}
void pd(int x){
if(! tg[x])return ;
tg[ls] ^= 1, tg[rs] ^= 1;
swap(s0[ls], s1[ls]);
swap(s0[rs], s1[rs]);
tg[x] = 0;
}
void mdf(int x, int l, int r, int ql, int qr){
if(ql <= l and r <= qr)return(void)(swap(s0[x], s1[x]), tg[x] ^= 1);
int mid = l + r >> 1; pd(x);
if(ql <= mid)mdf(ls, l, mid, ql, qr);
if(mid < qr)mdf(rs, mid + 1, r, ql, qr);
upd(x);
}
int nkp;
bool op;
int fd(int x, int l, int r){
if(l == r)return s1[x] ? l : - 1; pd(x); if(! s1[x])return - 1; int mid = l + r >> 1;
if(s1[ls])return fd(ls, l, mid);
else return fd(rs, mid + 1, r);
}
void qry(int x, int l, int r, int ql, int qr){
if(op)return ;
if(ql <= l and r <= qr){
int res = fd(x, l, r);
if(~ res)nkp = res, op = true;
return;
}
int mid = l + r >> 1; pd(x);
if(ql <= mid)qry(ls, l, mid, ql, qr);
if(op)return ;
if(mid < qr)qry(rs, mid + 1, r, ql, qr);
}
const int p = 1073741824;
signed main(){
n = rd(), m = rd();
for(int i = 1; i <= n; ++i)a[i] = rd();
for(int i = 1; i <= m; ++i){
int x = rd(), l = rd(), r = rd(), y;
q[i] = {x, l, r};
if(x == 1)q[i].x = rd();
}
for(int bit = 0; bit < 31; ++bit){
for(int i = 1; i <= n; ++i)b[i] = a[i] >> bit & 1;
build(1, 1, n);
for(int i = 1; i <= m; ++i)if(q[i].op == 1){
int x = q[i].x >> bit & 1;
if(! x)continue; mdf(1, 1, n, q[i].l, q[i].r);
}else{
op = false, nkp = q[i].r + 1; qry(1, 1, n, q[i].l, q[i].r);
q[i].ans += 1ll * (q[i].r - nkp + 1) * (1ll << bit) % p;
q[i].ans %= p;
}
}
for(int i = 1; i <= m; ++i)if(q[i].op ^ 1)printf("%lld\n", q[i].ans);
return 0;
}
线段树的拓展1(可持久化)
可持久化其实就是加了一个可以访问历史版本的功能,就比如我询问之前某次修改后的答案你可以和普通线段树复杂度一样
\(O(\log n)\)
回答。
考虑具体如何实现。其实每次修改操作,我们只会修改
\(O(\log n)\)
个点,于是我们就可以把这些点组成的链扯出来,对于每次操作重新“开”一颗线段树,就像下面这样。
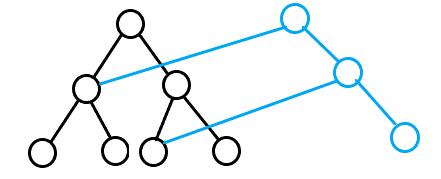
我们把每次操作看成一个树根,往下修改时就在原来的树上走,如果一个点不修改,就直接继承到现在的树上,否则就新开一个节点。然后其他东西就该咋弄咋弄,正常往这上面套各种线段树应该都行。
然后我们就不得不说一个非常重要的东西了。
可持久化权值线段树(主席树)
是的,我们如果让权值线段树可持久化,它就成了众所周知的主席树。这个东西能够查询静态区间第
\(k\)
小。至于动态区间第
\(k\)
小嘛,在外面再套一个树状数组不就行了?
先说静态的。我们把输入每一个数看成一次操作,而每次操作就是在值域中修改一个点。然后询问的时候就可以看成前缀和。在树上走的时候,对于寻找当前区间
\([l,r]\)
中值域里的第
\(k\)
大,我就正常线段树二分,但是同时二分两棵线段树,对于一个
\(mid\)
,前一半的值域在
\([l,r]\)
中数的个数
等价于
\([1,r]\)
中数的个数减去
\([1,l-1]\)
中数的个数
。然后就可以直接做了。
P3834 板子
以及
P1533 可怜的狗狗
双倍经验(真就直接复制)
代码如下:
int n, m, a[N], b[N], tt;
int rt[N << 5], c[N << 5], nd, ls[N << 5], rs[N << 5];
void upd(int &x, int y, int l, int r, int p){
x = ++nd; c[x] = c[y] + 1;
if(l == r)return; int mid = l + r >> 1;
if(p <= mid)rs[x] = rs[y], upd(ls[x], ls[y], l, mid, p);
else ls[x] = ls[y], upd(rs[x], rs[y], mid + 1, r, p);
}
int qry(int x, int y, int l, int r, int k){
if(l == r)return l; int mid = l + r >> 1, res = c[ls[x]] - c[ls[y]];
if(res >= k)return qry(ls[x], ls[y], l, mid, k);
return qry(rs[x], rs[y], mid + 1, r, k - res);
}
signed main(){
n = rd(), m = rd();
for(int i = 1; i <= n; ++i)a[i] = b[i] = rd();
sort(b + 1, b + 1 + n);
tt = unique(b + 1, b + 1 + n) - b - 1;
for(int i = 1; i <= n; ++i)a[i] = lower_bound(b + 1, b + 1 + tt, a[i]) - b, upd(rt[i], rt[i - 1], 1, tt, a[i]);
for(int i = 1; i <= m; ++i){
int l = rd(), r = rd(), k = rd();
printf("%d\n", b[qry(rt[r], rt[l - 1], 1, tt, k)]);
}
return 0;
}
然后考虑动态区间怎么做。
我们可以给主席树套一棵树状数组,每次暴力修改完在树状数组上维护,注意树状数组记录的其实只是每一棵主席树的树根,所以跑树状数组每一个点时要在对应的主席树上进行修改。查询可类比上文,上文中我们记录了两个树根,现在我们可以把树状数组上的一些相关的树根开两个数组记一下,每次二分就把所有树的答案累加起来,其他部分与上面类似不再赘述。
代码如下:
namespace SGT{
int nd, rt[N << 9], ls[N << 9], rs[N << 9], c[N << 9];
void gotols(){
for(int i = 1; i <= c1; ++i)q1[i] = ls[q1[i]];
for(int i = 1; i <= c2; ++i)q2[i] = ls[q2[i]];
}
void gotors(){
for(int i = 1; i <= c1; ++i)q1[i] = rs[q1[i]];
for(int i = 1; i <= c2; ++i)q2[i] = rs[q2[i]];
}
void upd(int &x, int l, int r, int p, int y){
if(! x)x = ++nd; c[x] += y;
if(l == r)return; int mid = l + r >> 1;
if(p <= mid)upd(ls[x], l, mid, p, y);
else upd(rs[x], mid + 1, r, p, y);
}
int qryk(int l, int r, int k){
if(l == r)return l; int mid = l + r >> 1, res = 0;
for(int i = 1; i <= c1; ++i)res -= c[ls[q1[i]]];
for(int i = 1; i <= c2; ++i)res += c[ls[q2[i]]];
if(res >= k)return gotols(), qryk(l, mid, k);
return gotors(), qryk(mid + 1, r, k - res);
}
int qryrk(int l, int r, int k){
if(l == r)return 0; int mid = l + r >> 1, res = 0;
if(k <= mid)return gotols(), qryrk(l, mid, k);
for(int i = 1; i <= c1; ++i)res -= c[ls[q1[i]]];
for(int i = 1; i <= c2; ++i)res += c[ls[q2[i]]];
return gotors(), res + qryrk(mid + 1, r, k);
}
}
using namespace SGT;
namespace BIT{
int lb(int x){return x & - x;}
void get(int l, int r){
c1 = c2 = 0;
for(int i = l - 1; i; i -= lb(i))q1[++c1] = rt[i];
for(int i = r; i; i -= lb(i))q2[++c2] = rt[i];
}
void mdf(int p, int y){
int x = lower_bound(b + 1, b + 1 + tt, a[p]) - b;
for(; p <= n; p += lb(p))upd(rt[p], 1, tt, x, y);
}
int kth(int l, int r, int k){get(l, r); return qryk(1, tt, k);}
int rk(int l, int r, int k){int kk = lower_bound(b + 1, b + 1 + tt, k) - b; get(l, r); return qryrk(1, tt, kk) + 1;}
}
首先分析题目性质,想想我们的答案有什么特点。因为是找最大中位数,是不是应该可以二分啊。假设当前二分一个
\(mid\)
,有一个套路就是把大于等于它的赋值成一,否则为零,然后看求子段和是否大于等于零即可判断。对于这道题,就是中间确定部分的可以用值域线段树维护,左右两边再分别开一个线段树维护前后缀最大子段和就行。
然后关于代码,就是放的我的远古时期写的
我自己都看的难受
神秘代码。
#include<bits/stdc++.h>
#define s(x) tr[x].sum
#define ls(x) tr[x].lson
#define rs(x) tr[x].rson
#define lm(x) tr[x].lmx
#define rm(x) tr[x].rmx
#define lc(x) tr[x].ncl
#define rc(x) tr[x].ncr
using namespace std;
const int N = 2e4 + 10;
int n, m, a[N], num[N], cnt, rt[N], idq, x1, x2, x3, x4;
int L(int x){return lower_bound(num + 1, num + cnt + 1, x) - num;}
struct tree
{
int sum, lmx, rmx;
int lson, rson;
bool ncl, ncr;
}tr[N * 40];
vector < int > c[N];
void upd(int x)
{
s(x) = s(ls(x)) + s(rs(x));
lm(x) = max(lm(ls(x)), s(ls(x)) + lm(rs(x)));
rm(x) = max(rm(rs(x)), s(rs(x)) + rm(ls(x)));
}
int build(int l, int r)
{
int x = ++idq;
if(l == r)
{
if(L(a[l]) < 2)s(x) = lm(x) = rm(x) = - 1;
else s(x) = lm(x) = rm(x) = 1;
return x;
}
int mid = l + r >> 1; lc(x) = rc(x) = 1;
ls(x) = build(l, mid); rs(x) = build(mid + 1, r);
upd(x); return x;
}
int modify(int x, int y, int l, int r, int to, int val, bool cc)
{
if(!cc)x = ++idq;
if(l == r)
{
s(x) = lm(x) = rm(x) = val;
return x;
}
int mid = l + r >> 1;
if(to <= mid)
{
if(!rc(x)) rs(x) = rs(y);
if(!lc(x))lc(x) = 1, ls(x) = modify(x, ls(y), l, mid, to, val, 0);
else ls(x) = modify(ls(x), ls(y), l, mid, to, val, 1);
}
else
{
if(!lc(x)) ls(x) = ls(y);
if(!rc(x))rc(x) = 1, rs(x) = modify(x, rs(y), mid + 1, r, to, val, 0);
else rs(x) = modify(rs(x), rs(y), mid + 1, r, to, val, 1);
}
upd(x); return x;
}
int query(int x, int l, int r, int L, int R)
{
if(L <= l and r <= R)return s(x);
int mid = l + r >> 1; int ret = 0;
if(L <= mid)ret += query(ls(x), l, mid, L, R);
if(mid < R)ret += query(rs(x), mid + 1, r, L, R);
return ret;
}
tree query1(int x, int l, int r, int L, int R)
{
if(L <= l and r <= R)return tr[x];
int mid = l + r >> 1;
if(L <= mid and mid < R)
{
tree ret;
tree le = query1(ls(x), l, mid, L, R);
tree ri = query1(rs(x), mid + 1, r, L, R);
ret.sum = le.sum + ri.sum;
ret.lmx = max(le.lmx, le.sum + ri.lmx);
return ret;
}
else if(L <= mid)return query1(ls(x), l, mid, L, R);
else return query1(rs(x), mid + 1, r, L, R);
}
tree query2(int x, int l, int r, int L, int R)
{
if(L <= l and r <= R)return tr[x];
int mid = l + r >> 1;
if(L <= mid and mid < R)
{
tree ret;
tree le = query2(ls(x), l, mid, L, R);
tree ri = query2(rs(x), mid + 1, r, L, R);
ret.sum = le.sum + ri.sum;
ret.rmx = max(ri.rmx, ri.sum + le.rmx);
return ret;
}
else if(L <= mid)return query2(ls(x), l, mid, L, R);
else return query2(rs(x), mid + 1, r, L, R);
}
bool check(int val)
{
int sz = 0;
if(x2 + 2 <= x3) sz = query(rt[val], 1, n, x2 + 1, x3 - 1);
int sr = query1(rt[val], 1, n, x3, x4).lmx;
int sl = query2(rt[val], 1, n, x1, x2).rmx;
return (sl + sz + sr) >= 0;
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)scanf("%d", &a[i]), num[++cnt] = a[i];
sort(num + 1, num + cnt + 1);
cnt = unique(num + 1, num + cnt + 1) - num - 1;
for(int i = 1; i <= n; i++)c[L(a[i])].push_back(i);
rt[1] = build(1,n);
for(int i = 2; i <= cnt; i++)for(int j = 0; j < c[i - 1].size(); j++)
{
int go = c[i - 1][j];
rt[i] = modify(rt[i], rt[i - 1], 1, n, go, - 1, rt[i] > 0);
}
scanf("%d", &m);
int las = 0;
int d[6];
while(m--)
{
scanf("%d %d %d %d", &x1, &x2, &x3, &x4);
d[1] = (x1 + las) % n;
d[2] = (x2 + las) % n;
d[3] = (x3 + las) % n;
d[4] = (x4 + las) % n;
sort(d + 1, d + 5);
x1 = d[1] + 1, x2 = d[2] + 1, x3 = d[3] + 1, x4 = d[4] + 1;
int l = 1, r = cnt;
int ans = 0;
while(l <= r)
{
int mid = l + r >> 1;
if(check(mid))ans = mid, l = mid + 1;
else r = mid - 1;
}
las = num[ans];
printf("%d\n", las);
}
return 0;
}
套路题。考虑我们每次记录
\(val\)
上次存在的位置,查询区间
\([l,r]\)
就是在
\(rt_r\)
子树中找满足出现时间小于
\(l\)
的最小
\(val\)
。用主席树维护最小值即可。
void upd(int &x, int y, int l, int r, int p, int val){
if(! x)x = ++tot; if(l == r)return(void)(ans[x] = val); int mid = l + r >> 1;
if(p <= mid)rs[x] = rs[y], upd(ls[x], ls[y], l, mid, p, val);
else ls[x] = ls[y], upd(rs[x], rs[y], mid + 1, r, p, val);
ans[x] = min(ans[ls[x]], ans[rs[x]]);
}
int qry(int x, int l, int r, int lim){
if(l == r)return l; int mid = l + r >> 1;
if(ans[ls[x]] < lim)return qry(ls[x], l, mid, lim);
else return qry(rs[x], mid + 1, r, lim);
}
signed main(){
// fileio(fil);
n = rd() + 1, m = rd();
for(int i = 1, x; i < n; ++i){
x = rd() + 1; if(x > n)rt[i] = rt[i - 1];
else upd(rt[i], rt[i - 1], 1, n, x, i);
}
for(int i = 1; i <= m; ++i){
int l = rd(), r = rd();
printf("%d\n", qry(rt[r], 1, n, l) - 1);
}
return 0;
}
线段树的拓展2(线段树合并)
注意合并要用
动态开点线段树
,不然复杂度会变成
\(O(n\log^2n)\)
的,因为线段树有
\(O(n\log n)\)
个节点,合并又是
\(O(\log n)\)
的。
怎么合并呢?我们还是在树上走,如果走到一点地方时存在节点(可能是一个或两个)为空,就可以直接返回另一个节点,否则就往下递归,到叶子时合并回来即可。但是乍一看这不是爆炸了吗?所以接下来我们需要
口胡
细致分析一下复杂度。
容易发现:在合并两棵树的过程中走到有空节点的时候就返回了,相当于走一个点就会删掉一些点,所以总复杂度不会超过总点数也就是
\(O(n\log n)\)
。
讲题前先谈谈我对于线段树合并的理解。首先为什么需要合并线段树,就是因为对于一些问题我们需要合并的信息是
\(O(n)\)
级别的,对于这类式子我们肯定需要一种
\(O(\log)\)
的方式去优化。然后就是如何去理解合并的过程,因为如果真的每一个点都开一个线段树那肯定爆炸没得说。其实我们是把每个点对应在一段区间上,或是下标或是值域,然后对于每一个点的线段树动态开点,最后是合并过程中并不是单纯的加加减减,而是要根据你的式子去还原整个过程,或许你现在还不太懂,但等你看了后面某道题后你便会恍然大悟。
然后看一道板子。
P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并
观察到是在树上修改,于是可以联想到某个经典套路,将树上路径转化成差分。具体的,对于一条路径
\((u,v)\)
,设
\(t=lca(u,v)\)
,则我可以把对于
\((u,v)\)
的操作看成对于
\((root,u)\)
和
\((root,v)\)
的操作还有
\((root,t)\)
和
\((root,fa_t)\)
的逆操作。然后考虑对每个点开线段树。本题可以用颜色做线段树下标,然后就似乎是单点修改(直接线段树二分)加上线段树合并。
然后稍微注意一下树上合并时需要跑一遍 dfs 序,然后递归返回时合并。
void dfs1(int u, int f){
dep[u] = dep[fa[u] = f] + 1, sz[u] = 1;
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == f)continue;
dfs1(v, u); sz[u] += sz[v];
if(sz[son[u]] < sz[v])son[u] = v;
}
}
void dfs2(int u, int top){
tp[u] = top;
if(! son[u])return; dfs2(son[u], top);
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == fa[u] or v == son[u])continue;
dfs2(v, v);
}
}
int lca(int u, int v){
while(tp[u] != tp[v]){
if(dep[tp[u]] < dep[tp[v]])swap(u, v);
u = fa[tp[u]];
}
return dep[u] < dep[v] ? u : v;
}
void upd(int x){
if(s[ls[x]] > s[rs[x]] or (s[ls[x]] == s[rs[x]] and col[ls[x]] < col[rs[x]]))return(void)(s[x] = s[ls[x]], col[x] = col[ls[x]]);
s[x] = s[rs[x]], col[x] = col[rs[x]];
}
void md(int &p, int l, int r, int c, int y){
if(! p)p = ++tot;
if(l == r)return(void)(s[p] += y, col[p] = c);
int mid = l + r >> 1;
if(c <= mid)md(ls[p], l, mid, c, y);
else md(rs[p], mid + 1, r, c, y);
upd(p);
}
int merge(int a, int b, int l, int r){
if(! a or ! b)return a | b;
if(l == r)return s[a] += s[b], a;
int mid = l + r >> 1;
ls[a] = merge(ls[a], ls[b], l, mid);
rs[a] = merge(rs[a], rs[b], mid + 1, r);
upd(a); return a;
}
void dfs(int u){
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == fa[u])continue;
dfs(v); rt[u] = merge(rt[u], rt[v], 1, 100000);
}
if(s[rt[u]])ans[u] = col[rt[u]];
}
signed main(){
n = rd(), q = rd();
for(int i = 1; i < n; ++i){
int u = rd(), v = rd();
add(u, v); add(v, u);
}
dfs1(1, 0); dfs2(1, 1);
for(int i = 1; i <= q; ++i){
int u = rd(), v = rd(), w = rd();
md(rt[u], 1, 100000, w, 1); md(rt[v], 1, 100000, w, 1);
int f = lca(u, v);
md(rt[f], 1, 100000, w, - 1); md(rt[fa[f]], 1, 100000, w, - 1);
}
dfs(1);
for(int i = 1; i <= n; ++i)printf("%d\n", ans[i]);
return 0;
}
怎么感觉有点过于板子了?
对于求第
\(k\)
大的问题我们用值域线段树,然后考虑怎么解决连通性?然后你会发现直接并查集维护,然后并查集就是菊花图,对每朵花的花心开一棵线段树,然后正常合并即可。
int fd(int x){
return x == f[x] ? x : f[x] = fd(f[x]);
}
void upd(int x){
s[x] = s[ls[x]] + s[rs[x]];
}
void md(int &p, int l, int r, int y){
if(! p)p = ++cnt;
if(l == r)return(void)(++s[p]);
int mid = l + r >> 1;
if(y <= mid)md(ls[p], l, mid, y);
else md(rs[p], mid + 1, r, y);
upd(p);
}
int merge(int a, int b, int l, int r){
if(! a or ! b)return a | b;
if(l == r)return s[a] += s[b], a;
int mid = l + r >> 1;
ls[a] = merge(ls[a], ls[b], l, mid);
rs[a] = merge(rs[a], rs[b], mid + 1, r);
upd(a); return a;
}
int qry(int p, int l, int r, int y){
if(l == r)return l;
int mid = l + r >> 1, ans;
if(s[ls[p]] >= y)ans = qry(ls[p], l, mid, y);
else ans = qry(rs[p], mid + 1, r, y - s[ls[p]]);
return ans;
}
void sol1(){
int x = rd(), y = rd();
x = fd(x), y = fd(y);
if(x == y)return;
f[y] = x; rt[x] = merge(rt[x], rt[y], 1, 100000);
}
signed main(){
n = rd(), m = rd();
for(int i = 1, x; i <= n; ++i)md(rt[i], 1, 100000, x = rd()), f[i] = i, pos[x] = i;
for(int i = 1; i <= m; ++i)sol1();
q = rd();
for(int i = 1; i <= q; ++i){
char c; cin >> c;
if(c == 'B')sol1();
else{
int x = rd(), y = rd(); x = fd(x);
if(s[rt[x]] < y){puts("-1"); continue;}
printf("%d\n", pos[qry(rt[x], 1, 100000, y)]);
}
}
return 0;
}
是不是觉得太简单了?那么来一点有难度的。
对于这道题我们可以很容易想到一个暴力 dp,设
\(f_{u,i}\)
表示
\(u\)
节点为第
\(i\)
大的数的概率。然后答案就是:
\]
然后开始转移,我们令当前点
\(u\)
的左儿子叫
\(l\)
,右儿子叫
\(r\)
,转移式子也就呼之欲出:
f_{r,i}\times p_u\times\sum_{j<i}f_{l,j}+
f_{l,i}\times (1-p_u)\times\sum_{j>i}f_{r,j}+
f_{r,i}\times (1-p_u)\times\sum_{j>i}f_{l,j}
\]
希望没有笔误
然后你就发现每次你都需要拿一段前缀出来转移,能不能优化一下啊?然而确实可以。考虑线段树维护,下标就是排名(dp 的第二维)。现在你就把每个
\(f_i\)
都看成二叉树上的点权,然后就可以合并了但是,
考虑这道题的合并并不是单纯的加减,我们上面推出的转移式中
\(f_i\)
是带了系数的,所以在合并时我们还需要记一下系数,那么系数又怎么求呢?
考虑把上面的式子拆完,就是对于线段树上一个点
\(i\)
,它的系数就是:
\]
说人话就是左边(下标)比它小的点乘上对应节点的概率
\(p\)
加上右边的。所以按照上面的实现就好了。
此题小结
其实线段树合并的本质就是优化状态转移。对于合并的顺序需要注意与线段树配套用的工具具体选择,然后对于合并的式子其实就是转移式子的复现,具体一点也就是
拆分再乘法分配律合并同类项
。
拓展到一般的题,我们最开始可以考虑 native 的想法,写出稍微暴力的转移与维护方式,然后再观察这些东西能不能通过什么性质把他们变得具有一些优美的性质,比如可加性、可减性、单调性之类的,最后在思考如何套线段树显得优雅。
代码
const db eps = 1e-8;
const ll inf = 1e18;
const int N = 3e5 + 5, p = 998244353;
ll qmi(ll x, ll y){
ll res = 1ll;
for(; y; y >>= 1, x = x * x % p)if(y & 1)res = res * x % p;
return res;
}
const ll ii = qmi(10000, p - 2);
int n, b[N], nd, m;
int rt[N << 5], ls[N << 5], rs[N << 5];
ll s[N << 5], tg[N << 5], f[N], a[N];
int fa[N], c[N], ch[N][2];
inline int jia(int x, int y){return x - p + y >= 0 ? x - p + y : x + y;}
void upd(int x){
s[x] = jia(s[ls[x]], s[rs[x]]);
}
void updd(int x, ll y){
if(! x)return;
s[x] = s[x] * y % p;
tg[x] = tg[x] * y % p;
}
void pd(int x){
if(tg[x] == 1)return;
updd(ls[x], tg[x]), updd(rs[x], tg[x]);
return (void)(tg[x] = 1);
}
void addin(int &x, int l, int r, int pos){
if(! x)tg[x = ++nd] = 1;
if(l == r)return(void)(s[x] = 1);
int mid = l + r >> 1; pd(x);
if(pos <= mid)addin(ls[x], l, mid, pos);
else addin(rs[x], mid + 1, r, pos);
upd(x);
}
int merge(int x, int y, int l, int r, ll sx, ll sy, ll pp){
if(! x or ! y)return updd(x | y, (x ? sx : sy)), x | y;
int mid = l + r >> 1; pd(x), pd(y);
ll lsl = s[ls[x]], rsl = s[rs[x]], lsr = s[ls[y]], rsr = s[rs[y]];
ls[x] = merge(ls[x], ls[y], l, mid, jia(sx, rsr * (p + 1 - pp) % p), jia(sy, rsl * (p + 1 - pp) % p), pp);
rs[x] = merge(rs[x], rs[y], mid + 1, r, jia(sx, lsr * pp % p), jia(sy, lsl * pp % p), pp);
return upd(x), x;
}
void dfs(int u){
if(! c[u])addin(rt[u], 1, m, a[u]);
if(c[u] == 1)dfs(ch[u][0]), rt[u] = rt[ch[u][0]];
if(c[u] == 2)dfs(ch[u][0]), dfs(ch[u][1]), rt[u] = merge(rt[ch[u][0]], rt[ch[u][1]], 1, m, 0, 0, a[u]);
}
void getans(int x, int l, int r){
if(! x)return;
if(l == r)return(void)(f[l] = s[x]);
int mid = l + r >> 1; pd(x);
getans(ls[x], l, mid); getans(rs[x], mid + 1, r);
}
int main(){
rd(n);
for(int i = 1; i <= n; ++i)rd(fa[i]), fa[i] ? ch[fa[i]][c[fa[i]]++] = i : 0;
for(int i = 1; i <= n; ++i){
rd(a[i]);
if(c[i])a[i] = a[i] * ii % p;
else b[++m] = a[i];
}
sort(b + 1, b + 1 + m);
for(int i = 1; i <= n; ++i)if(! c[i])a[i] = lower_bound(b + 1, b + 1 + m, a[i]) - b;
dfs(1); getans(rt[1], 1, m); ll ans = 0;
for(int i = 1; i <= m; ++i)ans = jia(ans, 1ll * i * b[i] % p * f[i] % p * f[i] % p);
wt(ans);
return 0;
}
(为什么没有线段树分裂?因为
我不会
感觉不太常见就先放了)
线段树的拓展3(李超线段树)
简单介绍一下,李超线段树维护了一些线段,它可以快速查询位置上纵坐标最大/小的线段编号以及数值。考虑这种东西就很适合去解决一些需要
从区间中找最值转移状态
的题。
然后讲一下实现与应用。
李超线段树的节点维护的是在
\(mid\)
处纵坐标最大的线段,所以实际维护的时候它就很暴力。直接在树上找到它的范围然后就每次暴力比较线段就完了。分析复杂度,查找是一只
\(\log\)
,然后暴力更新的时候因为两个一次函数最多只有一个交点,所以它之后递归一个子区间,复杂度也是一只
\(\log\)
,所以一共是两只
\(\log\)
。
查询时候就从根走到对应的叶子节点,走的时候顺路记一下最值就完了。
const int N = 1e5 + 5, mod1 = 39989, mod2 = 1e9 + 1;
const ll INF = 1e18;
int n;
lb k[N], b[N];
int sgt[N << 2];
#define ls x << 1
#define rs x << 1 | 1
lb calc(int x, int pos){
return k[x] * pos + b[x];
}
bool eq(lb a, lb b){
lb eps = 1e-10;
if(a - b < eps and b - a < eps)return true;
return false;
}
bool cmp(int x1, int x2, int pos){
lb a = calc(x1, pos), b = calc(x2, pos);
return a > b || (a == b and x1 < x2);
}
void _upd(int tmp, int x, int l, int r){
int mid = l + r >> 1;
if(cmp(tmp, sgt[x], mid))swap(tmp, sgt[x]);
if(cmp(tmp, sgt[x], l))_upd(tmp, ls, l, mid);
if(cmp(tmp, sgt[x], r))_upd(tmp, rs, mid + 1, r);
}
void upd(int x, int l, int r, int L, int R, int tmp){
if(L <= l and r <= R)return _upd(tmp, x, l, r);
int mid = l + r >> 1;
if(L <= mid)upd(ls, l, mid, L, R, tmp);
if(R > mid)upd(rs, mid + 1, r, L, R, tmp);
}
int qry(int x, int l, int r, int pos){
int mid = l + r >> 1, res = sgt[x];
if(l == r)return res;
int tmp = pos <= mid ? qry(ls, l, mid, pos) : qry(rs, mid + 1, r, pos);
if(cmp(tmp, res, pos))swap(res, tmp);
return res;
}
signed main(){
n = rd();
b[0] = - INF;
int ans = 0, cnt = 0;
for(int i = 1; i <= n; ++i){
int op = rd();
if(op == 0){
int pos = (rd() + ans + mod1 - 1) % mod1 + 1;
printf("%d\n", ans = qry(1, 1, mod1, pos));
}
else{
int x1 = rd(), y1 = rd(), x2 = rd(), y2 = rd();
x1 = (x1 + ans - 1) % mod1 + 1;
y1 = (y1 + ans - 1) % mod2 + 1;
x2 = (x2 + ans - 1) % mod1 + 1;
y2 = (y2 + ans - 1) % mod2 + 1;
if(x1 > x2)swap(x1, x2), swap(y1, y2);
if(x1 == x2)k[++cnt] = 0, b[cnt] = max(y1, y2);
else{
k[++cnt] = (lb)(y1 - y2) / (x1 - x2);
b[cnt] = y1 - k[cnt] * x1;
}
upd(1, 1, mod1, x1, x2, cnt);
}
}
return 0;
}
然后讲一些应用吧(?)
其实李超线段树
最主要
的运用还是结合着斜率优化 dp 一起考,本来我想放在后面与 dp 的结合的,想想还是算了。但是我在这一块的题写的很少,所以就会讲一点次要的。
P3081 [USACO13MAR] Hill Walk G
我们从
\((0,0)\)
开始走。如果直接建李超线段树那么当我们想要取下面部分的线段时就出问题了,所以我们就需要一个支持删除的东西维护它。于是考虑平衡树。
然后走的时候我们是横坐标排序,所以现在就只用考虑纵坐标。在每次走到一个线段的终点时我们需要看可行区间中比当前线段低一层的是谁。然后就想到把线段全部丢到平衡树里面,通过某种排序方使这些线段从高到低排好序。
那么如何判断两个线段的高低呢?我们通过下图来分析。
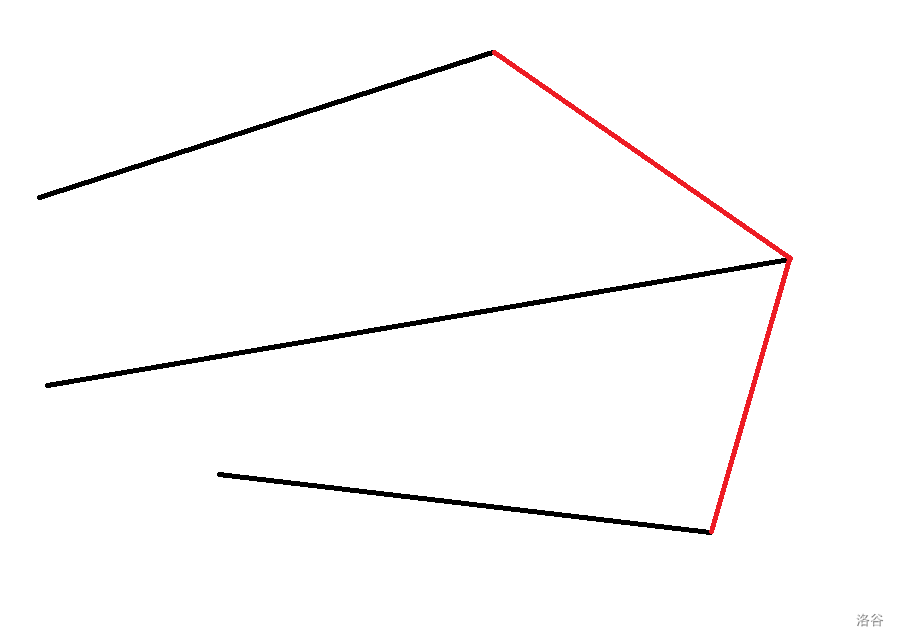
如果我要比较上面两条线段,我首先会去看它们右端点的位置。显然后者更靠右,然后我们把它们的右端点连接起来(如图红线)。如果前者更高(如图),那么
红线的斜率就会小于后面那条线段的斜率
,否则就会是图片下半部分的情况。于是我们比较线段之间的优先级时就可以先比较右端点再比较斜率了。
bool operator <(line x, line y){
if(x.c < y.c)return 1ll * (y.c - x.c) * (y.d - y.b) < 1ll * (y.d - x.d) * (y.c - y.a);
return 1ll * (x.c - y.c) * (x.d - x.b) > 1ll * (x.c - x.a) * (x.d - y.d);
}
注意如果直接用除法可能精度会炸。
然后就从左往右扫一遍,把线段该加入平衡树的就加进来,该删的就删掉。如果删掉的是当前所在的区间就在平衡树里查找一个比它低一层的线段然后更新答案。实际实现时可以用
set
代替平衡树。
int main(){
rd(n);
for(int i = 1; i <= n; ++i)rd(l[i].a, l[i].b, l[i].c, l[i].d), p[i - 1 << 1 | 1] = {l[i].a, l[i].b, i}, p[i << 1] = {l[i].c, l[i].d, i}, l[i].id = i;
s.ins(l[1]); sort(p + 1, p + 1 + (n << 1));
for(int i = 2; i <= (n << 1); ++i)
if(p[i].x == l[p[i].id].a)s.ins(l[p[i].id]);
else if(p[i].id == cur){
set < line > :: iterator it = s.find(l[p[i].id]);
if(it == s.begin())break;
++ans; it--;
cur = it -> id;
}
else s.del(l[p[i].id]);
wt(ans);
return 0;
}
本来有一道题的但是我把它放到树剖套线段树里面了。
本来还有一道题但是我把它又放到 dp 优化里面了。
所以因为各种原因,李超线段树就写到此为止吧!但是我能够保证你能在后面的内容中找到李超线段树的影子。
线段树的拓展4(扫描线)
这里只讲狭义扫描线也就是扫面积并,至于广义的扫面线等之后有空我会单独写一篇博客详细讲解。
就简单讲讲扫面积并。以从上往下扫为例,我们可以把图形拆成若干
平行于横轴的代表加一减一的线段
。每经过一个线段,这个奇形怪状的图形的横截长度就会发生变化,我们可以每次维护这个变化,并统计出上一次的横截长度对应的面积。然后对于经过线段,我们可以看成区间的加减,查询就是询问区间内非零个数。
int n, cnt[N << 2], top;
ll f[N << 2], y[N << 2], ans;
struct node{
ll x1, y1, y2;
int op;
bool operator < (const node &rhs)const {
return x1 < rhs.x1;
}
}a[N << 2];
#define ls x << 1
#define rs x << 1 | 1
void upd(int x, int l, int r){
if(cnt[x])return (void)(f[x] = y[r] - y[l - 1]);
f[x] = f[ls] + f[rs];
}
void modify(int x, int l, int r, int L, int R, int op){
if(L <= l and r <= R){cnt[x] += op; upd(x, l, r); return;}
int mid = l + r >> 1;
if(L <= mid)modify(ls, l, mid, L, R, op);
if(R > mid)modify(rs, mid + 1, r, L, R, op);
upd(x, l, r);
}
signed main(){
//freopen(, stdin);
//freopen(, stdout);
n = rd();
for(int i = 1; i <= n; ++i){
ll x1 = rd(), y1 = rd(), x2 = rd(), y2 = rd();
a[++top] = {x1, y1, y2, 1}; y[top] = y1;
a[++top] = {x2, y1, y2, - 1}; y[top] = y2;
}
sort(y + 1, y + 1 + top);
sort(a + 1, a + 1 + top);
n = unique(y + 1, y + 1 + top) - y - 1;
for(int i = 1; i <= top; ++i){
ans += f[1] * (a[i].x1 - a[i - 1].x1);
int l = lower_bound(y + 1, y + 1 + n, a[i].y1) - y;
int r = lower_bound(y + 1, y + 1 + n, a[i].y2) - y;
modify(1, 1, n, l + 1, r, a[i].op);
}
printf("%lld", ans);
return 0;
}
线段树的拓展5(树套树)
维护高维信息时,单纯的线段树显然无法胜任,这时我们就需要
简洁好写的 cdq 而不是使一样的
树套树。
树套树一般只套两层,套三层是真的没法写。对于两层的树来说,一般里层就是非常正常的树,它会正常地维护信息,然后外层的树有一点变化,因为外层的树不是维护一些信息而是一些树,所以为了方便我们就维护树根的信息。然后讲一讲修改。
其实也没啥好讲的,就是外层跑一遍,
只要是有关联的点都要修改!
需要修改的就去里层跑,然后递归往上更新就行。
查询就正常查询,找到区间后从直接返回答案变成查询里层。
有一道比板子简单一点的题放在主席树里面了,这里就直接放板子吧。然后这种东西讲多少遍都不如自己看别人写得好的代码然后自己想一遍。
namespace SGT{
int nd, rt[N << 9], ls[N << 9], rs[N << 9], c[N << 9];
void gotols(){
for(int i = 1; i <= c1; ++i)q1[i] = ls[q1[i]];
for(int i = 1; i <= c2; ++i)q2[i] = ls[q2[i]];
}
void gotors(){
for(int i = 1; i <= c1; ++i)q1[i] = rs[q1[i]];
for(int i = 1; i <= c2; ++i)q2[i] = rs[q2[i]];
}
void upd(int &x, int l, int r, int p, int y){
if(! x)x = ++nd; c[x] += y;
if(l == r)return; int mid = l + r >> 1;
if(p <= mid)upd(ls[x], l, mid, p, y);
else upd(rs[x], mid + 1, r, p, y);
}
int qryk(int l, int r, int k){
if(l == r)return l; int mid = l + r >> 1, res = 0;
for(int i = 1; i <= c1; ++i)res -= c[ls[q1[i]]];
for(int i = 1; i <= c2; ++i)res += c[ls[q2[i]]];
if(res >= k)return gotols(), qryk(l, mid, k);
return gotors(), qryk(mid + 1, r, k - res);
}
int qryrk(int l, int r, int k){
if(l == r)return 0; int mid = l + r >> 1, res = 0;
if(k <= mid)return gotols(), qryrk(l, mid, k);
for(int i = 1; i <= c1; ++i)res -= c[ls[q1[i]]];
for(int i = 1; i <= c2; ++i)res += c[ls[q2[i]]];
return gotors(), res + qryrk(mid + 1, r, k);
}
}
using namespace SGT;
namespace BIT{
int lb(int x){return x & - x;}
void get(int l, int r){
c1 = c2 = 0;
for(int i = l - 1; i; i -= lb(i))q1[++c1] = rt[i];
for(int i = r; i; i -= lb(i))q2[++c2] = rt[i];
}
void mdf(int p, int y){
int x = lower_bound(b + 1, b + 1 + tt, a[p]) - b;
for(; p <= n; p += lb(p))upd(rt[p], 1, tt, x, y);
}
int kth(int l, int r, int k){get(l, r); return qryk(1, tt, k);}
int rk(int l, int r, int k){int kk = lower_bound(b + 1, b + 1 + tt, k) - b; get(l, r); return qryrk(1, tt, kk) + 1;}
int pre(int l, int r, int k){
k = rk(l, r, k) - 1; return k > 0 ? b[kth(l, r, k)] : - INF;
}
int suf(int l, int r, int k){
k = rk(l, r, k + 1); return k < r - l + 2 ? b[kth(l, r, k)] : INF;
}
}
虽然这看上去很树套树+树剖但是其实可以将答案差分再合并一下扔掉一个
\(\log\)
,这样维护前缀主席树,查询时就查四棵树即可,最后就是
\(O(n\log^2n)\)
。但是我在看完题后根本没管太多,看到三只
\(\log\)
能过就写完树套树就水灵灵地过了((
void dfs1(int u, int f){
dep[u] = dep[fa[u] = f] + 1, sz[u] = 1;
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to; if(v == f)continue;
dfs1(v, u); sz[u] += sz[v];
if(sz[son[u]] < sz[v])son[u] = v;
}
}
void dfs2(int u, int tp){
top[u] = tp; dfn[u] = ++tim, rk[tim] = u;
if(son[u])dfs2(son[u], tp);
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v ^ fa[u] and v ^ son[u])dfs2(v, v);
}
}
void gotols(){
for(int i = 1; i <= c1; ++i)q1[i] = ls[q1[i]];
for(int i = 1; i <= c2; ++i)q2[i] = ls[q2[i]];
}
void gotors(){
for(int i = 1; i <= c1; ++i)q1[i] = rs[q1[i]];
for(int i = 1; i <= c2; ++i)q2[i] = rs[q2[i]];
}
void upd(int &x, int l, int r, int pos, int y){
if(! x)x = ++nd; s[x] += y;
if(l == r)return; int mid = l + r >> 1;
if(pos <= mid)upd(ls[x], l, mid, pos, y);
else upd(rs[x], mid + 1, r, pos, y);
}
int getsum(){
int sum = 0;
for(int i = 1; i <= c1; ++i)sum -= s[q1[i]];
for(int i = 1; i <= c2; ++i)sum += s[q2[i]];
return sum;
}
int qryk(int l, int r, int k){
if(l == r)return getsum() >= k ? l : 0; int mid = l + r >> 1, sum = 0;
for(int i = 1; i <= c1; ++i)sum -= s[rs[q1[i]]];
for(int i = 1; i <= c2; ++i)sum += s[rs[q2[i]]];
if(k <= sum)return gotors(), qryk(mid + 1, r, k);
return gotols(), qryk(l, mid, k - sum);
}
void get(int l, int r){
for(int i = l - 1; i; i -= i & - i)q1[++c1] = rt[i];
for(int i = r; i; i -= i & - i)q2[++c2] = rt[i];
}
void mdf(int pos, int y){
int x = lower_bound(b + 1, b + 1 + m, a[rk[pos]]) - b;
for(; pos <= n; pos += pos & - pos)upd(rt[pos], 1, m, x, y);
}
int kth(int u, int v,int k){
c1 = c2 = 0;
while(top[u] ^ top[v]){
if(dep[top[u]] < dep[top[v]])swap(u, v);
get(dfn[top[u]], dfn[u]);
u = fa[top[u]];
}
if(dep[u] > dep[v])swap(u, v);
get(dfn[u], dfn[v]); return qryk(1, m, k);
}
但是说实在的,实战中这玩意用的是真的少,一般时候还是 cdq 或者转化题意用复杂度更低的做法做。
线段树的一些高级玩法
这一部分主要是一些其他的算法、思想与线段树的运用,其实最主要的思想还是寻找题目性质,然后线段树优化维护信息的过程。
那就先来看一些线段树与树剖的东西。
树剖+线段树
做过序列上给一些颜色求颜色段数量的题吧?如果我把它扔到树上会怎么样呢?
结果是根本不会怎么样。直接树剖把树变成链做,套上线段树就完了。
void add(int u, int v){
e[++cnt] = {hd[u], v}; hd[u] = cnt;
}
void dfs1(int u, int f){
dep[u] = dep[fa[u] = f] + 1; sz[u] = 1;
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == f)continue;
dfs1(v, u); sz[u] += sz[v];
if(sz[son[u]] < sz[v])son[u] = v;
}
}
void dfs2(int u, int top){
tp[u] = top; dfn[u] = ++tim, rk[tim] = u;
if(! son[u])return; dfs2(son[u], top);
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == fa[u] or v == son[u])continue;
dfs2(v, v);
}
}
struct node{
int len, l, r;
};
#define ls x << 1
#define rs x << 1 | 1
void upd(int x){
lc[x] = lc[ls], rc[x] = rc[rs];
s[x] = s[ls] + s[rs] - (rc[ls] == lc[rs]);
}
void build(int x, int l, int r){
if(l == r)return(void)(lc[x] = rc[x] = a[rk[l]], s[x] = 1);
int mid = l + r >> 1;
build(ls, l, mid); build(rs, mid + 1, r);
upd(x);
}
void pd(int x){
if(! lz[x])return;
lc[ls] = rc[ls] = lz[x];
lc[rs] = rc[rs] = lz[x];
s[ls] = s[rs] = 1;
lz[ls] = lz[rs] = lz[x]; lz[x] = 0;
}
void mdfy(int x, int l, int r, int L, int R, int c){
if(L <= l and r <= R)return(void)(lc[x] = rc[x] = lz[x] = c, s[x] = 1);
int mid = l + r >> 1; pd(x);
if(L <= mid)mdfy(ls, l, mid, L, R, c);
if(R > mid)mdfy(rs, mid + 1, r, L, R, c);
upd(x);
}
node qry(int x, int l, int r, int L, int R){
if(L <= l and r <= R)return {s[x], lc[x], rc[x]};
int mid = l + r >> 1; node res, t; pd(x);
res = {0, 0, 0};
if(L <= mid)res = qry(ls, l, mid, L, R);
if(R > mid){
t = qry(rs, mid + 1, r, L, R);
if(! res.len)return t;
res.len += t.len - (rc[ls] == lc[rs]);
res.r = t.r;
}
return res;
}
void mpath(int u, int v, int c){
while(tp[u] != tp[v]){
if(dep[tp[u]] < dep[tp[v]])swap(u, v);
mdfy(1, 1, n, dfn[tp[u]], dfn[u], c);
u = fa[tp[u]];
}
if(dep[u] > dep[v])swap(u, v);
mdfy(1, 1, n, dfn[u], dfn[v], c);
}
int qpath(int u, int v){
int pr1 = 0, pr2 = 0, ans = 0;
while(tp[u] != tp[v]){
if(dep[tp[u]] < dep[tp[v]])swap(u, v), swap(pr1, pr2);
node res = qry(1, 1, n, dfn[tp[u]], dfn[u]);
ans += res.len - (pr1 == res.r);
pr1 = res.l; u = fa[tp[u]];
}
if(dep[u] > dep[v])swap(u, v), swap(pr1, pr2);
node res = qry(1, 1, n, dfn[u], dfn[v]);
ans += res.len - (pr1 == res.l) - (pr2 == res.r);
return ans;
}
这道是不是太简单了一点?那就加强一下!
这下看懂了!
其实颜色段的处理不成问题,我们需要思考的是树根的变化应该如何高效处理。
这个时候我们就可以分类讨论一下树根的位置了。如果树根就是询问点那直接输出全局的答案;如果树根
不在当前询问点
\(u\)
的子树内
,是不是对
\(u\)
根本没有影响啊!最后就剩一种——在
\(u\)
的某棵子树内,这时候我们肯定要先找到是哪一棵子树,然后用全局减去这棵子树就行。
那么如何快速找子树呢?我们可以类比树剖求 LCA 的过程,然后就做完了。找子树和其他操作都是
\(O(n\log n)\)
的。
void add(int u, int v){
e[++cnt] = {hd[u], v}; hd[u] = cnt;
}
void dfs1(int u, int f){
dep[u] = dep[fa[u] = f] + 1; sz[u] = 1;
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == f)continue;
dfs1(v, u); sz[u] += sz[v];
if(sz[son[u]] < sz[v])son[u] = v;
}
}
void dfs2(int u, int top){
tp[u] = top; dfn[u] = ++tim, rk[tim] = u;
if(! son[u])return; dfs2(son[u], top);
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == fa[u] or v == son[u])continue;
dfs2(v, v);
}
}
#define ls x << 1
#define rs x << 1 | 1
void upd(int x){
mi[x] = min(mi[ls], mi[rs]);
}
void build(int x, int l, int r){
if(l == r)return(void)(mi[x] = a[rk[l]]);
int mid = l + r >> 1;
build(ls, l, mid); build(rs, mid + 1, r);
upd(x);
}
void pd(int x){
if(! lz[x])return;
mi[ls] = mi[rs] = lz[x];
lz[ls] = lz[rs] = lz[x]; lz[x] = 0;
}
void mdfy(int x, int l, int r, int L, int R, int c){
if(L <= l and r <= R)return(void)(mi[x] = lz[x] = c);
int mid = l + r >> 1; pd(x);
if(L <= mid)mdfy(ls, l, mid, L, R, c);
if(R > mid)mdfy(rs, mid + 1, r, L, R, c);
upd(x);
}
ll qry(int x, int l, int r, int L, int R){
if(L <= l and r <= R)return mi[x];
int mid = l + r >> 1; ll res = INF; pd(x);
if(L <= mid)res = qry(ls, l, mid, L, R);
if(R > mid)res = min(res, qry(rs, mid + 1, r, L, R));
return res;
}
void mpath(int u, int v, int c){
while(tp[u] != tp[v]){
if(dep[tp[u]] < dep[tp[v]])swap(u, v);
mdfy(1, 1, n, dfn[tp[u]], dfn[u], c);
u = fa[tp[u]];
}
if(dep[u] > dep[v])swap(u, v);
mdfy(1, 1, n, dfn[u], dfn[v], c);
}
ll qtree(int u){
if(u == root)return mi[1];
if(dfn[root] < dfn[u] or dfn[root] >= dfn[u] + sz[u])return qry(1, 1, n, dfn[u], dfn[u] + sz[u] - 1);
int v = root;
while(tp[u] != tp[v]){
v = tp[v];
if(fa[v] == u)break;
v = fa[v];
}
if(tp[u] == tp[v])v = rk[dfn[u] + 1];
return min(qry(1, 1, n, 1, dfn[v] - 1), qry(1, 1, n, dfn[v] + sz[v], n));
}
好了也该来一道那啥一点的题了(
如果你会 LCT 而且代码能力强的话建议直接无脑做就完了。
考虑不会 LCT 的人会怎么做。如果用数据结构啥的维护删边可能不太现实,所以考虑倒着做就把删边变成了加边。然后就是如何维护两点之间桥的数量。我可以先把初始的桥给处理出来,跑一下 tarjan 然后图就成了一棵树,然后考虑加边操作意味着什么。如果现在需要将
\((u,v)\)
加入图中,那么树上
\(u,v\)
之间的
路径上的桥
就都没了,因为构成环。所以每次加边操作都可以看成区间赋值,然后树剖套一个果的线段树就做完了。
void addx(int u, int v){
ex[++cntx] = {hdx[u], v}; hdx[u] = cntx;
}
void tarjan(int u, int fa){
id[u] = low[u] = ++seq;
st.push(u);
for(int i = hdx[u]; i; i = ex[i].nxt){
int v = ex[i].to;
if(v == fa)continue;
if(! id[v])tarjan(v, u);
low[u] = min(low[u], low[v]);
}
if(low[u] == id[u]){
++ct;
while(st.top() ^ u){
col[st.top()] = ct;
st.pop();
}
col[u] = ct; st.pop();
}
}
void add(int u, int v){
e[++cnt] = {hd[u], v}; hd[u] = cnt;
}
void dfs1(int u, int f){
dep[u] = dep[fa[u] = f] + 1; sz[u] = 1;
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == f)continue;
dfs1(v, u); sz[u] += sz[v];
if(sz[son[u]] < sz[v])son[u] = v;
}
}
void dfs2(int u, int top){
tp[u] = top; dfn[u] = ++tim, rk[tim] = u;
if(! son[u])return; dfs2(son[u], top);
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == fa[u] or v == son[u])continue;
dfs2(v, v);
}
}
#define ls x << 1
#define rs x << 1 | 1
void upd(int x){
s[x] = s[ls] + s[rs];
}
void build(int x, int l, int r){
if(l == r)return(void)(s[x] = 1);
int mid = l + r >> 1;
build(ls, l, mid); build(rs, mid + 1, r);
upd(x);
}
void pd(int x, int l, int r){
if(! lz[x])return;
int mid = l + r >> 1;
s[ls] = s[rs] = 0;
lz[ls] = lz[rs] = lz[x]; lz[x] = 0;
}
void mdfy(int x, int l, int r, int L, int R, int c){
if(L <= l and r <= R)return(void)(s[x] = c, lz[x] = 1);
int mid = l + r >> 1; pd(x, l, r);
if(L <= mid)mdfy(ls, l, mid, L, R, c);
if(R > mid)mdfy(rs, mid + 1, r, L, R, c);
upd(x);
}
ll qry(int x, int l, int r, int L, int R){
if(L <= l and r <= R)return s[x];
int mid = l + r >> 1, res = 0; pd(x, l, r);
if(L <= mid)res = qry(ls, l, mid, L, R);
if(R > mid)res += qry(rs, mid + 1, r, L, R);
return res;
}
void mpath(int u, int v, int c){
while(tp[u] != tp[v]){
if(dep[tp[u]] < dep[tp[v]])swap(u, v);
mdfy(1, 1, n, dfn[tp[u]], dfn[u], c);
u = fa[tp[u]];
}
if(dep[u] > dep[v])swap(u, v);
mdfy(1, 1, n, dfn[u] + 1, dfn[v], c);
}
int qpath(int u, int v){
int res = 0;
while(tp[u] != tp[v]){
if(dep[tp[u]] < dep[tp[v]])swap(u, v);
res += qry(1, 1, n, dfn[tp[u]], dfn[u]);
u = fa[tp[u]];
}
if(dep[u] > dep[v])swap(u, v);
return res + qry(1, 1, n, dfn[u] + 1, dfn[v]);
}
signed main(){
n = rd(), m = rd();
for(int i = 1; i <= m; ++i){
E[i].u = rd(), E[i].v = rd();
if(E[i].u > E[i].v)swap(E[i].u, E[i].v);
++mp[mkp(E[i].u, E[i].v)];
}
while(1){
q[++tot][0] = rd();
if(q[tot][0] == - 1)break;
q[tot][1] = rd(), q[tot][2] = rd();
if(q[tot][1] > q[tot][2])swap(q[tot][1], q[tot][2]);
if(! q[tot][0])--mp[mkp(q[tot][1], q[tot][2])];
}
--tot;
for(int i = 1; i <= m; ++i){
int u = E[i].u, v = E[i].v;
if(mp[mkp(u, v)])addx(u, v), addx(v, u);
}
tarjan(1, 0);
for(int i = 1; i <= m; ++i){
int u = E[i].u, v = E[i].v;
if(mp[mkp(u, v)] and col[u] ^ col[v])add(col[u], col[v]), add(col[v], col[u]);
}
for(int i = 1; i <= tot; ++i)q[i][1] = col[q[i][1]], q[i][2] = col[q[i][2]];
dfs1(1, 0); dfs2(1, 1); build(1, 1, n);
for(int i = tot; i; --i){
if(q[i][0])ans[++tt] = q[i][1] == q[i][2] ? 0 : qpath(q[i][1], q[i][2]);
else mpath(q[i][1], q[i][2], 0);
}
for(int i = tt; i; --i)printf("%d\n", ans[i]);
return 0;
}
对于这种题我们需要翻译题目信息。
像文中的两个点求 lca 深度的过程我们能不能用另一种视角去看待?我们可以看成一个点到根的路径加一,另一个点再查询其到一的路径的权值和。然后就好做了。具体的讲,我们可以把区间与点求 lca 的深度转换成两个前缀和相减,这不就直接离线以后扫描线扫一遍的事?
void dfs1(int u, int f){
dep[u] = dep[f] + 1, sz[u] = 1;
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
dfs1(v, u); sz[u] += sz[v];
if(sz[son[u]] < sz[v])son[u] = v;
}
}
void dfs2(int u, int tp){
top[u] = tp, dfn[u] = ++tim, rk[tim] = u;
if(son[u])dfs2(son[u], tp);
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to; if(v ^ son[u])dfs2(v, v);
}
}
int s[N << 2], tg[N << 2];
#define ls x << 1
#define rs x << 1 | 1
int ad(int x, int y){
return x += y, x >= p ? x - p : x;
}
void upd(int x){
s[x] = ad(s[ls], s[rs]);
}
void pd(int x, int l, int r){
if(! tg[x])return; int mid = l + r >> 1;
tg[ls] = ad(tg[ls], tg[x]), tg[rs] = ad(tg[rs], tg[x]);
s[ls] = ad(s[ls], tg[x] * (mid - l + 1) % p);
s[rs] = ad(s[rs], tg[x] * (r - mid) % p);
return(void)(tg[x] = 0);
}
void mdf(int x, int l, int r, int ql, int qr){
if(ql <= l and r <= qr)return(void)(s[x] = ad(s[x], (r - l + 1) >= p ? r - l + 1 - p : r - l + 1), ++tg[x]);
int mid = l + r >> 1; pd(x, l, r);
if(ql <= mid)mdf(ls, l, mid, ql, qr);
if(mid < qr)mdf(rs, mid + 1, r, ql, qr);
upd(x);
}
int qry(int x, int l, int r, int ql, int qr){
if(ql <= l and r <= qr)return s[x];
int mid = l + r >> 1, res = 0; pd(x, l, r);
if(ql <= mid)res = qry(ls, l, mid, ql, qr);
if(mid < qr)res = ad(res, qry(rs, mid + 1, r, ql, qr));
return res;
}
void up(int u){
while(top[u] ^ 1){
mdf(1, 1, n, dfn[top[u]], dfn[u]);
u = fa[top[u]];
}
mdf(1, 1, n, 1, dfn[u]);
}
int fd(int u){
int sum = 0;
while(top[u] ^ 1){
sum = ad(sum, qry(1, 1, n, dfn[top[u]], dfn[u]));
u = fa[top[u]];
}
return ad(sum, qry(1, 1, n, 1, dfn[u]));
}
struct qay{
int x, id, o;
};
vector < qay > q[N];
int ans[N];
int main(){
rd(n, Q);
for(int i = 2; i <= n; ++i)rd(fa[i]), add(++fa[i], i);
dfs1(1, 0), dfs2(1, 1);
for(int i = 1, l, r, x; i <= Q; ++i){
rd(l, r, x);
q[++r].pb({++x, i, 1});
q[l].pb({x, i, - 1});
}
for(int i = 1; i <= n; ++i){
up(i);
for(qay j : q[i])ans[j.id] = (ans[j.id] + p + j.o * fd(j.x)) % p;
}
for(int i = 1; i <= Q; ++i)wt(ans[i]), pc('\n');
return 0;
}
感觉找的题是不是太简单了
也许看到修改的式子中带了一个
\(dis\)
你会马上想到差分,但是仔细一想似乎不太对。因为它每次询问路径最小值,但是每次的操作相对独立,这样一看您觉得这是否更像线段覆盖的题。
想通了后这道题的做法就呼之欲出了,直接树剖套李超线段树板子做完。但是加线段的地方还要在 lca 处分讨一下。
void dfs1(int u, int f){
dep[u] = dep[fa[u] = f] + 1; cnt[u] = 1;
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to; if(v == f)continue; dis[v] = dis[u] + e[i].w;
dfs1(v, u); if(cnt[son[u]] < cnt[v])son[u] = v;
cnt[u] += cnt[v];
}
}
void dfs2(int u, int top){
tp[u] = top;
dfn[u] = ++seq; rk[dfn[u]] = u;
if(! son[u])return; dfs2(son[u], top);
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to;
if(v == fa[u] or v == son[u])continue;
dfs2(v, v);
}
}
int lca(int u, int v){
while(tp[u] != tp[v]){
if(dep[tp[u]] < dep[tp[v]])swap(u, v);
u = fa[tp[u]];
}
return dep[u] < dep[v] ? u : v;
}
ll k[N], b[N], c[N << 3];
#define ls x << 1
#define rs x << 1 | 1
ll calc(int x, int pos){
return k[x] * dis[rk[pos]] + b[x];
}
bool cmp(int x1, int x2, int pos){
ll a = calc(x1, pos), b = calc(x2, pos);
return a < b or (a == b and x1 < x2);
}
void updd(int x, int l, int r){
ll a = calc(sgt[x], l), b = calc(sgt[x], r);
c[x] = min(c[x], min(a, b));
c[x] = min(c[x], min(c[ls], c[rs]));
}
void _upd(int tmp, int x, int l, int r){
int mid = l + r >> 1;
if(cmp(tmp, sgt[x], mid))swap(tmp, sgt[x]);
if(cmp(tmp, sgt[x], l))_upd(tmp, ls, l, mid);
if(cmp(tmp, sgt[x], r))_upd(tmp, rs, mid + 1, r);
updd(x, l, r);
}
void upd(int x, int l, int r, int L, int R, int tmp){
if(L <= l and r <= R)return _upd(tmp, x, l, r);
int mid = l + r >> 1;
if(L <= mid)upd(ls, l, mid, L, R, tmp);
if(R > mid)upd(rs, mid + 1, r, L, R, tmp);
updd(x, l, r);
}
ll qry(int x, int l, int r, int L, int R){
if(L <= l and r <= R)return c[x];
int mid = l + r >> 1; ll res = min(calc(sgt[x], max(l, L)), calc(sgt[x], min(r, R)));
if(L <= mid)res = min(res, qry(ls, l, mid, L, R));
if(R > mid)res = min(res, qry(rs, mid + 1, r, L, R));
return res;
}
void usum(int u, int v, int tmp){
while(tp[u] != tp[v]){
if(dep[tp[u]] < dep[tp[v]])swap(u, v);
upd(1, 1, n, dfn[tp[u]], dfn[u], tmp);
u = fa[tp[u]];
}
if(dfn[u] < dfn[v])swap(u, v);
upd(1, 1, n, dfn[v], dfn[u], tmp);
}
ll qsum(int u, int v){
ll res = INF;
while(tp[u] != tp[v]){
if(dep[tp[u]] < dep[tp[v]])swap(u, v);
res = min(res, qry(1, 1, n, dfn[tp[u]], dfn[u]));
u = fa[tp[u]];
}
if(dfn[u] < dfn[v])swap(u, v);
res = min(res, qry(1, 1, n, dfn[v], dfn[u]));
return res;
}
signed main(){
for(int i = 0; i < N << 3; ++i)c[i] = INF;
n = rd(), m = rd(); int lcnt = 0;
for(int i = 1; i < n; ++i){
int u = rd(), v = rd(); ll w = rd();
add(u, v, w); add(v, u, w);
}
dfs1(1, 0); dfs2(1, 1); b[0] = INF;
for(int i = 1; i <= m; ++i){
int op = rd(), u = rd(), v = rd();
if(op ^ 1)printf("%lld\n", qsum(u, v));
else{
int t = lca(u, v);
ll A = rd(), B = rd();
k[++lcnt] = - A; b[lcnt] = A * dis[u] + B;
usum(u, t, lcnt);
k[++lcnt] = A; b[lcnt] = A * (dis[u] - 2 * dis[t]) + B;
usum(t, v, lcnt);
}
}
return 0;
}
线段树与 dp
dp 有关的技巧与知识在此不赘述,可以翻一下我写的 dp 的一些博客。这里是线段树专题,所以我想讲一点线段树的东西。
首先是何时用线段树的问题。如果 dp 式子中出现了需要葱区间转移的东西我们会先考虑记一下关键信息,转移时直接合并,当我们无法快速查找或合并时我们就会上线段树。
然后就是线段树需要维护什么?我们启用线段树的初衷是要维护一些不太好用数组记录的信息,或是转移或查询的时候不方便的东西。所以我们在维护线段树过程中就应该结合实际去记录,而不是把原来的信息原封不动扔进去。比如原来的信息差分后有良好的性质我就只需要把差分的东西丢进去,查询时在进行合并。
最后是选用什么线段树。当我们维护的信息只有可合并的特点时我们就上最普通的线段树,如果信息具有一定的可加可减性可以考虑可持久化。如果是高维信息就先看能不能 cdq,然后看树套树,最后考虑 kd-tree(虽然我不会这个,也就只能看看)。
因为是我很早以前做过的,还写了题解,所以就摘录的当时题解的原话。
因为铁球从高到低落下去,则每一个平台最短时间的贡献只会来源于它头上的一个(或几个)平台,所以是线性的,于是考虑dp。
考虑按照由低到高的顺序dp。令
\(dp[i][0/1]\)
表示从
\(x\)
轴到第
\(i\)
个平台的左/右端点最短用时。
首先可以推出第
\(i\)
个平台上任意一点
\((k,a_i.h)\)
到
\(x\)
轴最短用时为:
\(\min(k-a_i.l+dp[i][0],a_i.r-k+dp[i][1])\)
然后平台间转移:
\]
就可以用数据结构维护
\(j\)
了。具体的,每次更新
\(i\)
的答案后用当前平台编号覆盖之前的平台编号,但是数据太大需要离散化一下。维护用线段树和
set
均可。
所以说这道题就这么被我用
set
水过了。但是因为我非常负责所以还是放一个代码:
int n, m, x, y, f[N][2];
struct line{
int h, l, r;
}a[N];
set < pair < int, int > > s;
bool cmp(line x, line y){
return x.h < y.h;
}
void upd(int &ff, int nw, int h, int j){
if(h - a[j].h > m)return;
if(! j)return(void)(ff = h);
ff = h - a[j].h + min(nw - a[j].l + f[j][0], a[j].r - nw + f[j][1]);
}
signed main(){
n = rd(); m = rd(); x = rd(); y = rd();
for(int i = 1; i <= n; ++i)a[i].h = rd(), a[i].l = rd(), a[i].r = rd();
memset(f, INF, sizeof f); sort(a + 1, a + 1 + n, cmp);
s.insert({INF, 0});
for(int i = 1; i <= n; ++i){
int lx = a[i].l, rx = a[i].r, hx = a[i].h;
auto lp = s.lower_bound({lx, 0}), rp = s.lower_bound({rx, 0});
upd(f[i][0], lx, hx, lp -> second); upd(f[i][1], rx, hx, rp -> second);
int tg = lp -> second;
for(; lp -> first <= rx; lp = s.erase(lp)); s.insert({lx, tg}); s.insert({rx, i});
}
int res; upd(res, x, y, s.lower_bound({x, 0}) -> second);
printf("%d", res);
return 0;
}
看一道典题。
P4655 [CEOI2017] Building Bridges
这个 dp 似乎就很一眼。
设
\(f_i\)
表示从
\(1\)
走到
\(i\)
的最小代价,然后转移方程就是:
\]
给
\(w\)
记一个前缀和,并把式子拆一拆,就变成了:
\]
然后把不变的提出来:
\]
现在的目标就是如何快速查询
\(\min\)
。如果你对于每一个
\(j\)
把所有与其有关的东西看成一个函数,再把
\(i\)
有关的
\(h_i\)
看成一个变量,我是不是就把
\(\min\)
里面的一坨抽象成了一个一次函数。我令
\(k=h_j,b=f_j+h_j^2-s_j\)
,然后这一坨就变成了
\(k\times h_i+b\)
,问题就变成在当前所有线段中查询位置
\(h_i\)
处的最小值,于是就李超线段树了。
int n;
ll h[N], w[N];
ll s[N], f[N];
namespace SGT{
ll k[N], b[N];
int sgt[M << 2];
#define ls x << 1
#define rs x << 1 | 1
const int lim = M - 3;
ll calc(int x, int pos){return k[x] * pos + b[x];}
bool cmp(int x1, int x2, int pos){
ll t1 = calc(x1, pos), t2 = calc(x2, pos);
return t1 < t2;
}
void upd(int x, int l, int r, int id){
int mid = l + r >> 1;
if(cmp(id, sgt[x], mid))swap(sgt[x], id);
if(cmp(id, sgt[x], l))upd(ls, l, mid, id);
if(cmp(id, sgt[x], r))upd(rs, mid + 1, r, id);
}
void mdf(int x, int l, int r, int ql, int qr, int id){
if(ql <= l and r <= qr)return(void)(upd(x, l, r, id));
int mid = l + r >> 1;
if(ql <= mid)mdf(ls, l, mid, ql, qr, id);
if(mid < qr)mdf(rs, mid + 1, r, ql, qr, id);
}
int qry(int x, int l, int r, int pos){
if(l == r)return sgt[x];
int mid = l + r >> 1, res;
res = pos <= mid ? qry(ls, l, mid, pos) : qry(rs, mid + 1, r, pos);
return cmp(res, sgt[x], pos) ? res : sgt[x];
}
}
using namespace SGT;
int main(){
rd(n); for(int i = 1; i <= n; ++i)rd(h[i]); b[0] = inf;
for(int i = 1; i <= n; ++i)rd(w[i]), s[i] = s[i - 1] + w[i];
for(int i = 1; i <= n; ++i){
int j = qry(1, 0, lim, h[i]);
if(i ^ 1)f[i] = f[j] + h[j] * h[j] - s[j] - 2 * h[i] * h[j] + h[i] * h[i] + s[i - 1];
k[i] = - 2 * h[i]; b[i] = f[i] + h[i] * h[i] - s[i];
mdf(1, 0, lim, 0, lim, i);
}
wt(f[n]);
return 0;
}
考虑令
\(f_i\)
表示前
\(i\)
盏灯能够照亮的最大前缀。考虑转移。
对于当前的灯有两种情况,一种是前面的灯照不到它,这时就不用管直接跳过,还有就是照的到就更新当前最大值。
但实际上还有一种就是当前的朝左,然后能被它照到的就全向右,这时
\(f_i=\max_{i-p_i\le j<i}\{j+p_j\}\)
。
然后其实用 st 表就可以维护了,但是这道题有一定的价值所以我还是放到这里了。
最后输出方案就倒推一遍即可。
void init(int nn){
f[0] = f[1] = 0;
for(int i = 1; i <= nn; ++i)op[i] = 0;
}
void make_st(){
for(int j = 1; j <= lg[n]; ++j)
for(int i = 1; i + (1 << j) - 1 <= n; ++i)st[i][j] = max(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
}
int query(int l, int r){
if(l > r)return 0;
int j = lg[r - l + 1];
return max(st[l][j], st[r - (1 << j) + 1][j]);
}
int find(int l, int r, int x){
int id = - 1;
while(l <= r){
int mid = l + r >> 1;
if(f[mid] >= x)id = mid, r = --mid;
else l = ++mid;
}
return id;
}
void solve(int x){
if(! x)return;
if(f[x] == f[x - 1])return (void)solve(x - 1);
if(f[x] == st[x][0] and f[x - 1] >= x)return (void)(op[x] = 1, solve(x - 1));
int y = find(0, x - 1, x - p[x] - 1);
for(int i = y + 1; i < x; ++i)op[i] = 1;
solve(y);
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T; cin >> T;
for(int i = 2; i < N; ++i)lg[i] = lg[i >> 1] + 1;
while(T--){
init(n);
cin >> n;
for(int i = 1; i <= n; ++i)cin >> p[i], st[i][0] = i + p[i];
make_st();
for(int i = 1; i <= n; ++i){
f[i] = f[i - 1];
if(f[i] >= i)f[i] = max(f[i], st[i][0]);
int id = find(0, i - 1, i - p[i] - 1);
if(id != - 1)f[i] = max(f[i], max(i - 1, query(id + 1, i - 1)));
}
// for(int i = 1; i <= n; ++i)cout << "f[" << i << "] = " << f[i] << ' '; cout << '\n';
if(f[n] < n){
cout << "NO" << '\n';
continue;
}
cout << "YES" << '\n';
solve(n);
for(int i = 1; i <= n; ++i)cout << (op[i] ? 'R' : 'L');
cout << '\n';
}
return 0;
}
线段树优化建图
顾名思义,就是在建图过程中可能会出现点向区间连边或区间向点连边的情况,这时就需要线段树优化建图,只是图上操作时复杂度多一只
\(\log\)
。
这道题就是出现了上述情况,在此重点讲建图的方法。首先我们需要满足区间能够与点联系起来,这就需要线段树的节点与点要相连。我们可以效仿线段树维护信息的方式,将树上的节点一层一层连起来,最后叶子节点其实就代表真正的点。
其次是我们多连的这些虚边不能影响答案。这时边权的设计就需要仔细考虑。比如此题是求最短路,所以我把边权设为零,那如果是跑网络流,我们的边权(容量)就应该设成正无穷。
下面代码只展示连边方法,相信能够看到这里的读者都会最短路。
void build(int x, int l, int r){
t[x].l = l, t[x].r = r;
if(l == r){
int n1 = l + (n << 3), n2 = x + (n << 2);
add(n1, x, 0); add(x, n1, 0);
add(n1, n2, 0); add(n2, n1, 0);
return;
}
int mid = l + r >> 1, t = n << 2;
add(x, ls, 0); add(x, rs, 0);
add(ls + t, x + t, 0); add(rs + t, x + t, 0);
build(ls, l, mid); build(rs, mid + 1, r);
}
void modify(int x, int L, int R, int u, ll w, bool op){
int l = t[x].l, r = t[x].r, mid = l + r >> 1;
int t1 = n << 2, t2 = n << 3;
if(L == l and r == R){
if(op)return (void)(add(x + t1, u + t2, w));
else return (void)(add(u + t2, x, w));
}
if(R <= mid)modify(ls, L, R, u, w, op);
else if(L > mid)modify(rs, L, R, u, w, op);
else{
modify(ls, L, mid, u, w, op);
modify(rs, mid + 1, R, u, w, op);
}
}
signed main(){
//freopen(,stdin);
//freopen(,stdout);
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> q >> s;
build(1, 1, n);
for(int i = 1, op, u, v, l, r; i <= q; ++i){
cin >> op >> u;
ll w;
if(op == 1){
cin >> v >> w;
add(u + (n << 3), v + (n << 3), w);
}
else{
cin >> l >> r >> w;
modify(1, l, r, u, w, op - 2);
}
}
s += (n << 3);
dijkstra();
for(int i = 1, t = n << 3; i <= n; ++i){
if(d[i + t] < 2e18)cout << d[i + t] << ' ';
else cout << - 1 << ' ';
}
return 0;
}
问题升级!如果是区间向区间连边呢?如果把区间抓出来对应连是
\(O(\log^2)\)
的,然后 bfs 也是
\(O(\log^2)\)
的所以就会被卡。这时我们可以继续建虚点,将区间与虚点连边即可。
void build(int x, int l, int r){
t[x].l = l, t[x].r = r;
if(l == r)return (void)(id[l] = x);
int mid = l + r >> 1, t = n << 2;
add(x, ls, 0); add(x, rs, 0);
add(ls + t, x + t, 0); add(rs + t, x + t, 0);
build(ls, l, mid); build(rs, mid + 1, r);
}
void modify(int x, int L, int R, int u, bool op){
int l = t[x].l, r = t[x].r, mid = l + r >> 1;
if(l == L and r == R){
if(op)return (void)(add(x + (n << 2), u, 0));
return (void)(add(u, x, 0));
}
if(R <= mid)modify(ls, L, R, u, op);
else if(L > mid)modify(rs, L, R, u, op);
else{
modify(ls, L, mid, u, op);
modify(rs, mid + 1, R, u, op);
}
}
signed main(){
//freopen(,stdin);
//freopen(,stdout);
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> s;
build(1, 1, n);
cnt = n << 3;
for(int i = 1, l1, l2, r1, r2; i <= m; ++i){
int u = ++cnt, v = ++cnt;
cin >> l1 >> r1 >> l2 >> r2;
add(v, u, 1); modify(1, l2, r2, u, 0); modify(1, l1, r1, v, 1);
u = ++cnt, v = ++cnt;
add(v, u, 1); modify(1, l1, r1, u, 0); modify(1, l2, r2, v, 1);
}
for(int i = 1, t = n << 2; i <= n; ++i){
add(id[i], id[i] + t, 0);
add(id[i] + t, id[i], 0);
}
s = id[s] + (n << 2);
bfs();
for(int i = 1; i <= n; ++i)cout << d[id[i]] << '\n';
return 0;
}
然后
车站分级
大家应该都做过吧?如果把它的数据范围改到
\(n=10^5\)
又该怎么做?
考虑线段树优化建图。每一趟车相当于一些区间向一些点连边,就像上面的题一样,每次新建一个虚点,区间连向虚点、虚点连向单点。只不过因为要跑 toposort,所以线段树上的边需要改成单向边,这时注意方向一定是从叶子连向根。代码懒得找就不放了。
线段树的更难的应用(杂题)
P10856 【MX-X2-T5】「Cfz Round 4」Xor-Forces
一道非常不错的题!
先找题目性质,然后发现操作一可以合并,所以只用考虑如何快速做完操作一并得到操作二的答案。先考虑如何在动态序列上维护颜色段,我们可以维护满足
\(col_{i-1}=col_{i}=col_{i+1}\)
的数量再用总数减去就是答案。对于区间的端点我们暴力判断就行因为不会超过
\(O(\log n)\)
。那么操作一又如何处理呢?
考虑每次操作后有的区间会交换但是有的却
保持相对静止
,然后建议随便写几个数用纸和笔手摸一下操作。
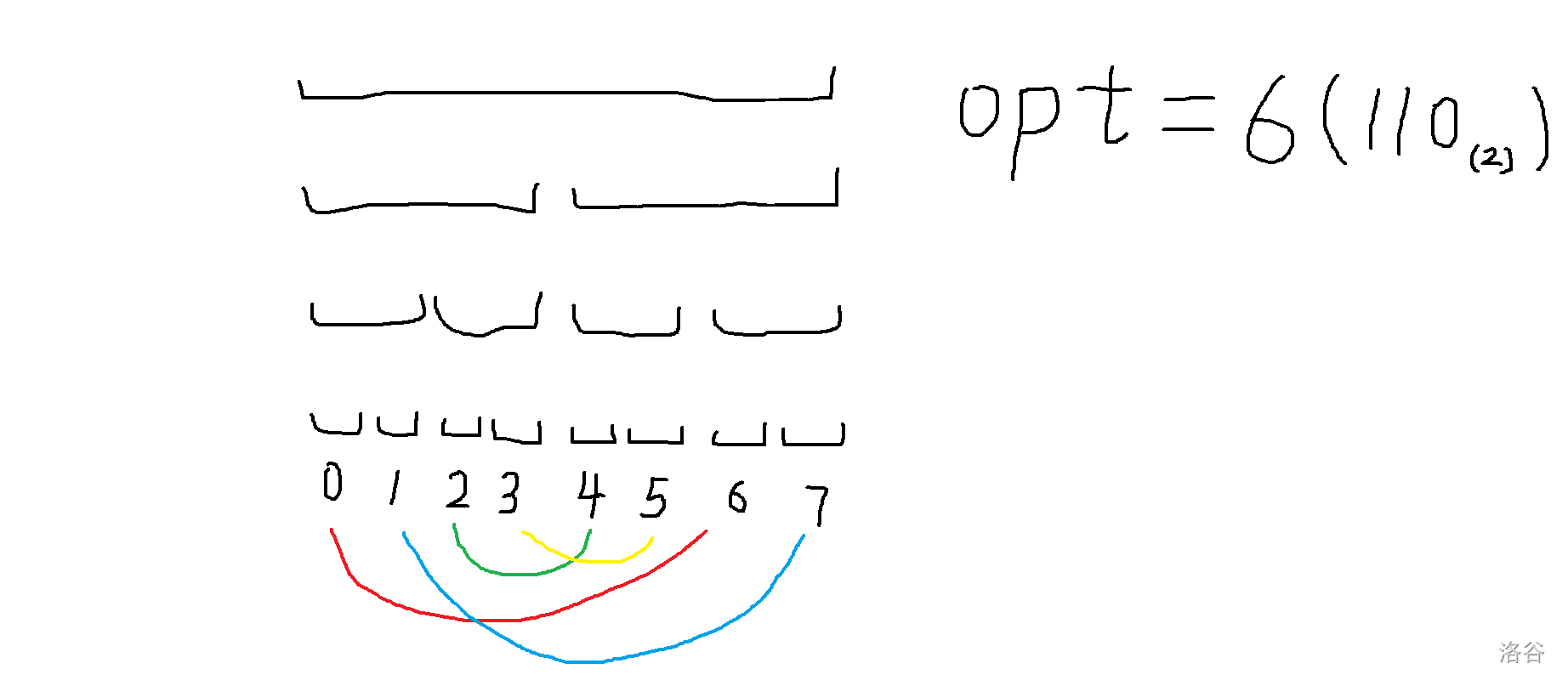
你会发现我其实是把
\([0,1]\)
这个区间平移到了
\([6,7]\)
,其他可以类比。试想对于线段树上一段长度为
\(len\)
的区间,我做操作一后出现的情况只会有
\(len\)
种。设异或上
\(sum\)
,若
\(sum>len\)
其实就可以看成
\(sum\bmod len\)
,因为把这些东西都放在二进制下你会发现他多出来的那些数位上的一都没有用,而
\(sum\)
取零到
\(len-1\)
时序列的变换方式又互不相同,所以有
\(len\)
种情况。然后我其实可以直接把这些情况记下来。时间复杂度是
\(\sum_{i=0}^{2^i\le len}\frac{len}{2^i}=2\times len\)
的,所以建树总复杂度还是
\(O(n\log n)\)
的。
然后其实就直接在线段树上走就行了,对于查询到的区间,若当前操作的值小于等于就可以直接把答案取出来,否则就需要
平移
到同一层的某个点上,调用它的答案。对于平移操作我们又如何处理呢?
我们可以记录一个数组
\(jump_{l,i}\)
代表序列上左端点是
\(l\)
且线段树节点大小为
\(2^i\)
的点是谁,然后跳的时候相当于二进制下
数位小于等于当前走到的点
就直接调用平移后的答案,大于等于的部分就异或上区间左端点直接跳,最后中点的答案就暴力合并即可。
(如果有点晕建议结合上面的图画一下)
代码:
void bld(int x, int l, int r){
int len = r - l, mid = l + r >> 1;
jump[l][lg[len]] = x; f[x].rsz(len);
if(l + 1 == r)return;
bld(ls, l, mid), bld(rs, mid, r);
for(int i = 0; i < len; ++i)
if(i < (len >> 1))f[x][i] = f[ls][i] + f[rs][i] + (a[mid - 1 ^ i] == a[mid ^ i]);
else f[x][i] = f[ls][i - (len >> 1)] + f[rs][i - (len >> 1)] + (a[mid - 1 ^ i] == a[mid ^ i]);
}
int qry(int x, int l, int r, int ql, int qr){
if(ql <= l and r - 1 <= qr)return f[jump[l ^ (opt >> lg[r - l] << lg[r - l])][lg[r - l]]][opt % (1 << lg[r - l])];
int mid = l + r >> 1, ansl(0), ansr(0); bool fl(false), fr(false);
if(ql < mid)fl = true, ansl = qry(ls, l, mid, ql, qr);
if(mid <= qr)fr = true, ansr = qry(rs, mid, r, ql, qr);
return fl ? (fr ? (ansl + ansr + (a[mid ^ opt] == a[mid - 1 ^ opt])) : ansl) : ansr;
}
此题性质就是考虑只要满足有三个数满足条件就行。然后中间的这个数是最特殊的!因为输入的数构成排列,假设我对当前点左边的点全染黑色(1),右边全染白色(0),如果
\(\exists t,col_{x+t}=1,col_{x-t}=0\)
那么就说明找到了。
然后我们就考虑如何快速查找与更新。如果像上面一样给位置染色,我如何快速判断呢?我可以在值域上染色,把这个 01 序列看成一个高位数,实际操作时我可以对于黑点和白点各维护一个高位数,然后就去比较他们的某几位是否是回文数。细想,这不就是哈希判断回文串吗?于是两棵线段树维护正/反哈希就行了。
但是因为以前数据过水导致我用
bitset
艹过了,现在也懒得写代码于是就咕了。
观察到限制是
\(\le x\)
所以我们直接离线下来按限制从小到大排序然后线段树合并暴力做。
P7834 [ONTAK2010] Peaks 加强版
考虑加强
现在你不可以离线。又应该这么做呢?
其实做法还是基于此题的限制
\(\le x\)
。因为有这个关系,所以我们可以建 kruskal 重构树。这样如果两个点能够互相抵达当且仅当它们的 lca 小于等于 x,于是我们就从当前点一直往上跳,直到不能再走到其他点。这一过程可以倍增实现,并且倍增同时能够维护出最大值。然后跳到最高点后我们就用主席树查询即可。
struct Edge{
int u, v; ll w;
friend bool operator < (Edge a, Edge b){
return a.w < b.w;
}
}E[M];
struct edge{
int nxt, to;
}e[M << 1];
void add(int u, int v){
e[++cnt] = {hd[u], v}, hd[u] = cnt; ++in[v];
}
int fd(int x){
return x == ff[x] ? x : ff[x] = fd(ff[x]);
}
void dfs(int u, int fa){
lq[dfn[++tim] = u] = tim, f[u][0] = fa;
for(int i = 1; (1 << i) <= n; ++i)f[u][i] = f[f[u][i - 1]][i - 1];
for(int i = hd[u]; i; i = e[i].nxt){
int v = e[i].to; if(v == fa)continue;
dfs(v, u), sz[u] += sz[v];
}
if(! sz[u])sz[u] = 1; rq[u] = tim;
}
int rt[N], ls[N << 5], rs[N << 5], t[N << 5];
void upd(int &x, int y, int l, ll r, int pos, int val){
if(! x)x = ++tot; t[x] = t[y] + val;
if(l == r)return; ll mid = l + r >> 1;
if(pos <= mid)rs[x] = rs[y], upd(ls[x], ls[y], l, mid, pos, val);
else ls[x] = ls[y], upd(rs[x], rs[y], mid + 1, r, pos, val);
}
int kth(int x, int y, int l, ll r, int k){
if(l == r)return l; ll mid = l + r >> 1, s = t[rs[y]] - t[rs[x]];
if(k > s)return kth(ls[x], ls[y], l, mid, k - s);
else return kth(rs[x], rs[y], mid + 1, r, k);
}
int qry(int u, int lim, int k){
for(int i = 23; ~ i; --i)if(f[u][i] and c[f[u][i]] <= lim)u = f[u][i];
if(sz[u] < k)return - 1;
return kth(rt[lq[u] - 1], rt[rq[u]], 0, inf, k);
}
signed main(){
// fileio(fil);
int mod;
mod = n = rd(), m = rd(), q = rd();
for(int i = 1; i <= n; ++i)h[i] = rd();
for(int i = 1; i <= (n << 1); ++i)ff[i] = i;
for(int i = 1; i <= m; ++i){
int u = rd(), v = rd(); ll w = rd();
E[i] = {u, v, w};
}
sort(E + 1, E + 1 + m);
for(int i = 1; i <= m; ++i){
int u = fd(E[i].u), v = fd(E[i].v); ll w = E[i].w;
if(u == v)continue;
ff[u] = ff[v] = ++n; c[n] = w;
add(n, u), add(n, v);
}
for(int i = 1; i <= n; ++i)if(! in[i])dfs(i, 0);
for(int i = 1; i <= n; ++i){
if(dfn[i] <= mod)upd(rt[i], rt[i - 1], 0, inf, h[dfn[i]], 1);
else rt[i] = rt[i - 1];
}
ll lastans = 0;
for(int i = 1; i <= q; ++i){
ll u = (rd() ^ lastans) % mod + 1, lim = rd() ^ lastans, k = (rd() ^ lastans) % mod + 1;
printf("%lld\n", lastans = qry(u, lim, k)); lastans = max(0ll, lastans);
}
return 0;
}
评价是:真的神仙题!
我们需要思考的是如何翻译题目。我们假设已经被安排的座位是一(黑点),否则是零(白点)。正常想法是类比一维的时候,我们记录区间内一的个数,然后看是否等于区间大小。这可以线段树维护。但是考虑到调换座位的操作会对一段区间造成影响,如果我每个都要
\(O(1)\)
修改肯定就炸了,我们就需要一种
可以合并的信息
去代替现在的。
区间操作我们可以想到区间加,那么我们现在能不能记录一些可加的信息来描述合法情况?
我们来考虑每一个点的情况,假设当前状态已经合法,现在是一个矩形然后四周可能有一圈白点。假设这个点是黑点,想想它满足什么性质时矩形合法而什么时候矩形不合法。本题最妙的地方来了!我们可以关注它周围点的状态来确定是否合法。具体的,如果这个点左边的点和上面的点有黑点,那么他就只能是矩形的一部分,否则它就必定为矩形的左上角,而左上角显然只有一个。也就是说我们要维护黑点
左边和上面都是白点的黑点
的数量,当数量为一时满足条件。
然后考虑白点周围状态。如果它周围有至少两个黑点那么当前状态就不合法。所以我们可以再记录一下
周围有至少两个黑点的白点
的数量,当数量为零时满足条件。
然后聪明如你,你会发现这两个状态需要同时满足,所以可以把它们放在一起维护。最后就是支持区间加,查询全局最小值数量。修改操作其实就是暴力交换后周围的一些点可能会有影响,把这些点重新算一遍就好了。
const int dir[4][2] = {1, 0, - 1, 0, 0, 1, 0, - 1};
int h, w, q;
vector < vector < int > > g;
int tt[N];
struct node{
int x, y, tim;
}a[N];
int res[N << 2], cnt[N << 2], tg[N << 2];
#define ls x << 1
#define rs x << 1 | 1
void upd(int x){
res[x] = min(res[ls], res[rs]);
cnt[x] = cnt[ls] * (res[x] == res[ls]) + cnt[rs] * (res[x] == res[rs]);
}
void init(int x, int l, int r){
if(l == r)return(void)(cnt[x] = 1);
int mid = l + r >> 1;
init(ls, l, mid), init(rs, mid + 1, r);
upd(x);
}
void pd(int x){
if(! tg[x])return;
tg[ls] += tg[x], res[ls] += tg[x];
tg[rs] += tg[x], res[rs] += tg[x];
return(void)(tg[x] = 0);
}
void mdf(int x, int l, int r, int ql, int qr, int y){
if(ql <= l and r <= qr)return(void)(res[x] += y, tg[x] += y);
int mid = l + r >> 1; pd(x);
if(ql <= mid)mdf(ls, l, mid, ql, qr, y);
if(mid < qr)mdf(rs, mid + 1, r, ql, qr, y);
upd(x);
}
int get(int x, int y){
if(x < 0 or y < 0 or x >= h or y >= w)return inf;
return a[g[x][y]].tim;
}
int loc(int x, int y){
if(x < 0 or y < 0 or x >= h or y >= w)return - 1;
return g[x][y];
}
void option(int i, int op){
vector < int > lp; int t1, t2;
lp.pb(get(a[i].x + 1, a[i].y));
lp.pb(get(a[i].x, a[i].y + 1));
lp.pb(t1 = get(a[i].x - 1, a[i].y));
lp.pb(t2 = get(a[i].x, a[i].y - 1));
sort(lp.bg(), lp.ed()); int lpos = lp[1];
if(a[i].tim > lpos)mdf(1, 1, h * w, lpos, a[i].tim - 1, op);
t1 = min(t1, t2); if(t1 > a[i].tim)mdf(1, 1, h * w, a[i].tim, t1 - 1, op);
}
int main(){
rd(h, w, q); g.rsz(h); for(int i = 0; i < h; ++i)g[i].rsz(w);
for(int i = 1; i <= h * w; ++i){
rd(a[i].x, a[i].y);
g[a[i].x][a[i].y] = a[i].tim = i;
tt[i] = i;
}
init(1, 1, h * w);
for(int i = 1; i <= h * w; ++i)option(i, 1);
for(int i = 1, u, v; i <= q; ++i){
rd(u, v); ++u, ++v;
int used[12], cc;
used[1] = u = tt[u], used[cc = 2] = v = tt[v];
int xx = a[u].x, yy = a[u].y;
for(int j = 0; j < 4; ++j){
int tmp = loc(xx + dir[j][0], yy + dir[j][1]);
if(~ tmp)used[++cc] = tmp;
}
xx = a[v].x, yy = a[v].y;
for(int j = 0; j < 4; ++j){
int tmp = loc(xx + dir[j][0], yy + dir[j][1]);
if(~ tmp)used[++cc] = tmp;
}
sort(used + 1, used + 1 + cc); cc = unique(used + 1, used + 1 + cc) - used - 1;
for(int j = 1; j <= cc; ++j)option(used[j], - 1);
swap(a[u].tim, a[v].tim);
swap(tt[a[u].tim], tt[a[v].tim]);
for(int j = 1; j <= cc; ++j)option(used[j], 1);
wt(cnt[1]); pc('\n');
}
return 0;
}
后记
从起稿开始(2024.11.6 16:00)到竣工(2024.11.8.15.26)一共花了我两天时间。其间我写了十道题左右,并重新梳理了暑假讲的和国庆拔高的
几乎
所有题目,当然一些太逆天的题我还是没能写完。从明天开始我就准备复习 dp 部分的内容,但可能很难再像这次写下这洋洋几千上万字了。今天下午,随着半期考试的落幕,没有停课的同学们也会陆续归队,机房不再冷清。但这样安静投入的去做一件事情是真的很好!每天回宿舍都很疲惫,晚上冼个澡,躺下就睡,早上总是 6:30 准时醒,生物钟就这样形成。
不知又要到何时,我内心才能如此平静?或许,改变自己的心态,既是一种挑战,也是一份礼物。当你成功克服自我后,也许会收获意想不到的惊喜!
但无论如何,ds 方面的内容算是弄完了。cdq 和整体二分我会在今天下午后半程复习完毕,下一次很系统的复习应该就要到 noip 后了,希望不要给自己留遗憾,也希望大家都能有光明的前途!