2024年11月

python bytecode解析

作者: wenmo8
时间: 2024-11-02
分类: 其它
评论

python bytecode解析

前言

我们的电脑是怎么运行的呢？
计算机内部的 CPU 处理器是个硅片，上面雕刻着精心布置的电路，输入特定的电流，就能得到另一种模式的电流，而且模式可以预测，给这些模式起上名字并赋予含义，我们就可以说这种电流模式代表加法，电脑的工作原理就是如此，我们起的这些名字叫做 CPU 指令，有时也被成为机器码。

_{[引自:James Bennett]}
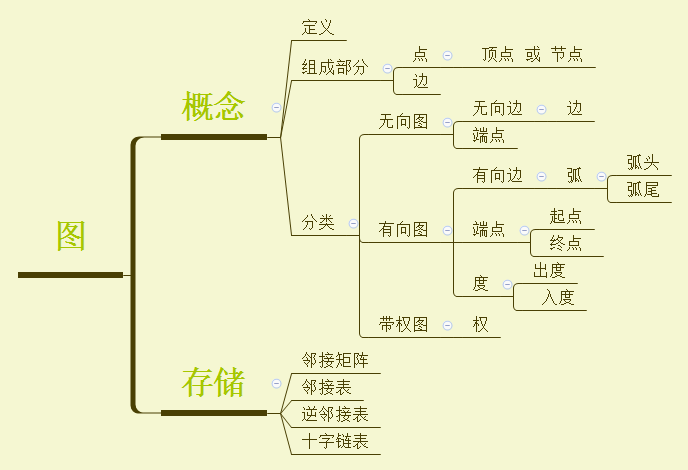
我们的编程语言是怎么运行的呢？一些语言通过编译器，直接将源代码编译成机器码，这些语言就是编译语言，还有一些语言解除解释器，直接在运行时把源代码解释为机器码，这些就是解释型语言。不过还有第三种语言，介于源代码和机器码之间，一些语言编译得到的指令，但是这种指令不能被现有的CPU直接运行，而需要解释器去理解，并将这些指令翻译为真实的 CPU 接受的二进制码，这种中间指令就是我们今天要说的bytecode（字节码），有很多语言属于此类比如java，C#，还有python。

Java编译的字节码运行在java虚拟机上，C#编译的字节码运行在.Net 虚拟机上，而Python 编译的字节码运行在 Python 虚拟机上。

‍

工作原理

CPython解释器在内部会将Python源代码编译成
字节码
，并缓存在
.pyc
文件中，目的是当再次执行该文件时，直接读取
.pyc
文件会更快，这样可以避免从源码重新编译到字节码，当然，Python再找到符合文件后，检查此文件的时间戳，如果发现字节码文件（文件在导入时就被编译完成）比源代码文件时间戳早（比如你修改过原文件），那么就会重新生成字节码，否则就会跳过此步骤。如果，Python在搜索时只找到了字节码而没有找到源代码文件，那么就会直接执行字节码文件（如果没有印象，请回想在模块导入时发生了什么）。然后，Python虚拟机执行字节码编译器发出的字节码。

‍

面向栈

这个是在看
码农高天
（一个非常厉害的pytohn核心开发者）的视频里学到的概念，CPython使用一个基于栈的虚拟机，也就是说，它完全是面向栈，这种数据结构的。就是不断地push、pop。

CPython使用3种类型的栈：

调用栈（call stack）。这是运行Python程序的主要结构，它为每个当前活动的函数调用，使用了一个东西
帧（frame）
，
栈底是程序的入口点，每个函数调用推送一个新的帧到调用栈，当函数调用返回后，这个帧被销毁
。
计算栈（evaluation stack，或称数据栈data stack）。在每个帧中，计算栈就是函数运行的地方，运行的代码大多数是由推入到这个栈中的东西组成的。在栈中操作它们，当函数被返回后，销毁它们。
块栈（block stack）。在每个帧中，块栈被Python用于跟踪某些类型的控制结构，如循环、
try/except
块和
with ... as ...
块，这些控制结构全部被推入到块栈中，当退出这些控制结构式，块栈被销毁，这将帮助Python了解任意给定时刻哪个块是活动的，比如一个continue或者break语句，这些可能影响结果的块。

大多数Python字节码指令操作的是当前调用栈的计算栈，虽然还有些指令可以做其他的事情，比如跳转到指定指令，或者操作块栈。

‍

字节码的阅读

其实还有
代码对象
和
字节码的工作
这两个概念没说，因为本文主要讲怎么阅读字节码，能够通过字节码手搓出py源码（是的，我是个CTFer），想了解更多的可以去本文末的推荐链接里看。

‍

dis模块

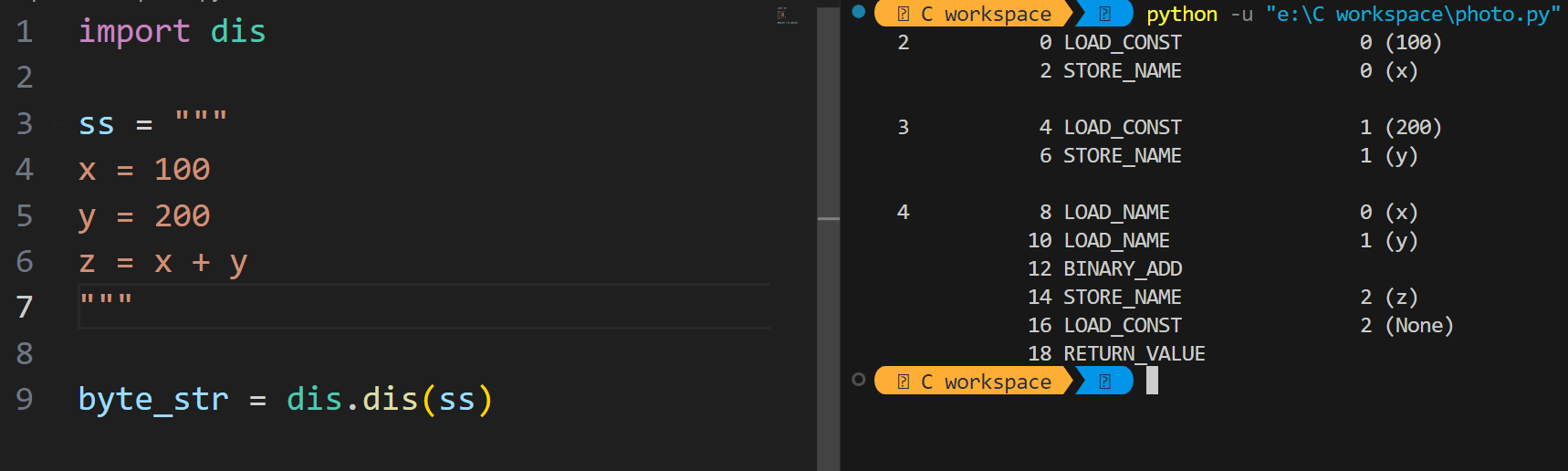
因为python代码运行是到字节码再到机器码一气呵成的，我们想要看到中间指令，需要借助python的标准库dis模块，它可以将py代码翻译成字节码。如下：

‍

案例

2024网鼎杯青龙组初赛的MISC02题目(1 解)，是一个linux内存镜像取证，前面繁琐的步骤略过，最后一步获得一个 flag.txt 文件，里面是python字节码，明显需要我们手搓还原py代码，如下：

 31         226 PUSH_NULL
            228 LOAD_NAME                8 (key_encode)
            230 LOAD_NAME                7 (key)
            232 PRECALL                  1
            236 CALL                     1
            246 STORE_NAME               7 (key)

 32         248 PUSH_NULL
            250 LOAD_NAME               10 (len)
            252 LOAD_NAME                7 (key)
            254 PRECALL                  1
            258 CALL                     1
            268 LOAD_CONST               7 (16)
            270 COMPARE_OP               2 (==)
            276 POP_JUMP_FORWARD_IF_FALSE    43 (to 364)

 33         278 PUSH_NULL
            280 LOAD_NAME                9 (sm4_encode)
            282 LOAD_NAME                7 (key)
            284 LOAD_NAME                5 (flag)
            286 PRECALL                  2
            290 CALL                     2
            300 LOAD_METHOD             11 (hex)
            322 PRECALL                  0
            326 CALL                     0
            336 STORE_NAME              12 (encrypted_data)

 34         338 PUSH_NULL
            340 LOAD_NAME                6 (print)
            342 LOAD_NAME               12 (encrypted_data)
            344 PRECALL                  1
            348 CALL                     1
            358 POP_TOP
            360 LOAD_CONST               2 (None)
            362 RETURN_VALUE

 32     >>  364 LOAD_CONST               2 (None)
            366 RETURN_VALUE

Disassembly of <code object key_encode at 0x14e048a00, file "make.py", line 10>:
 10           0 RESUME                   0

 11           2 LOAD_GLOBAL              1 (NULL + list)
             14 LOAD_FAST                0 (key)
             16 PRECALL                  1
             20 CALL                     1
             30 STORE_FAST               1 (magic_key)

 12          32 LOAD_GLOBAL              3 (NULL + range)
             44 LOAD_CONST               1 (1)
             46 LOAD_GLOBAL              5 (NULL + len)
             58 LOAD_FAST                1 (magic_key)
             60 PRECALL                  1
             64 CALL                     1
             74 PRECALL                  2
             78 CALL                     2
             88 GET_ITER
        >>   90 FOR_ITER               105 (to 302)
             92 STORE_FAST               2 (i)

 13          94 LOAD_GLOBAL              7 (NULL + str)
            106 LOAD_GLOBAL              9 (NULL + hex)
            118 LOAD_GLOBAL             11 (NULL + int)
            130 LOAD_CONST               2 ('0x')
            132 LOAD_FAST                1 (magic_key)
            134 LOAD_FAST                2 (i)
            136 BINARY_SUBSCR
            146 BINARY_OP                0 (+)
            150 LOAD_CONST               3 (16)
            152 PRECALL                  2
            156 CALL                     2
            166 LOAD_GLOBAL             11 (NULL + int)
            178 LOAD_CONST               2 ('0x')
            180 LOAD_FAST                1 (magic_key)
            182 LOAD_FAST                2 (i)
            184 LOAD_CONST               1 (1)
            186 BINARY_OP               10 (-)
            190 BINARY_SUBSCR
            200 BINARY_OP                0 (+)
            204 LOAD_CONST               3 (16)
            206 PRECALL                  2
            210 CALL                     2
            220 BINARY_OP               12 (^)
            224 PRECALL                  1
            228 CALL                     1
            238 PRECALL                  1
            242 CALL                     1
            252 LOAD_METHOD              6 (replace)
            274 LOAD_CONST               2 ('0x')
            276 LOAD_CONST               4 ('')
            278 PRECALL                  2
            282 CALL                     2
            292 LOAD_FAST                1 (magic_key)
            294 LOAD_FAST                2 (i)
            296 STORE_SUBSCR
            300 JUMP_BACKWARD          106 (to 90)

 15     >>  302 LOAD_GLOBAL              3 (NULL + range)
            314 LOAD_CONST               5 (0)
            316 LOAD_GLOBAL              5 (NULL + len)
            328 LOAD_FAST                0 (key)
            330 PRECALL                  1
            334 CALL                     1
            344 LOAD_CONST               6 (2)
            346 PRECALL                  3
            350 CALL                     3
            360 GET_ITER
        >>  362 FOR_ITER               105 (to 574)
            364 STORE_FAST               2 (i)

 16         366 LOAD_GLOBAL              7 (NULL + str)
            378 LOAD_GLOBAL              9 (NULL + hex)
            390 LOAD_GLOBAL             11 (NULL + int)
            402 LOAD_CONST               2 ('0x')
            404 LOAD_FAST                1 (magic_key)
            406 LOAD_FAST                2 (i)
            408 BINARY_SUBSCR
            418 BINARY_OP                0 (+)
            422 LOAD_CONST               3 (16)
            424 PRECALL                  2
            428 CALL                     2
            438 LOAD_GLOBAL             11 (NULL + int)
            450 LOAD_CONST               2 ('0x')
            452 LOAD_FAST                1 (magic_key)
            454 LOAD_FAST                2 (i)
            456 LOAD_CONST               1 (1)
            458 BINARY_OP                0 (+)
            462 BINARY_SUBSCR
            472 BINARY_OP                0 (+)
            476 LOAD_CONST               3 (16)
            478 PRECALL                  2
            482 CALL                     2
            492 BINARY_OP               12 (^)
            496 PRECALL                  1
            500 CALL                     1
            510 PRECALL                  1
            514 CALL                     1
            524 LOAD_METHOD              6 (replace)
            546 LOAD_CONST               2 ('0x')
            548 LOAD_CONST               4 ('')
            550 PRECALL                  2
            554 CALL                     2
            564 LOAD_FAST                1 (magic_key)
            566 LOAD_FAST                2 (i)
            568 STORE_SUBSCR
            572 JUMP_BACKWARD          106 (to 362)

 18     >>  574 LOAD_CONST               4 ('')
            576 LOAD_METHOD              7 (join)
            598 LOAD_FAST                1 (magic_key)
            600 PRECALL                  1
            604 CALL                     1
            614 STORE_FAST               1 (magic_key)

 19         616 LOAD_GLOBAL             17 (NULL + print)
            628 LOAD_FAST                1 (magic_key)
            630 PRECALL                  1
            634 CALL                     1
            644 POP_TOP

 20         646 LOAD_GLOBAL              7 (NULL + str)
            658 LOAD_GLOBAL              9 (NULL + hex)
            670 LOAD_GLOBAL             11 (NULL + int)
            682 LOAD_CONST               2 ('0x')
            684 LOAD_FAST                1 (magic_key)
            686 BINARY_OP                0 (+)
            690 LOAD_CONST               3 (16)
            692 PRECALL                  2
            696 CALL                     2
            706 LOAD_GLOBAL             11 (NULL + int)
            718 LOAD_CONST               2 ('0x')
            720 LOAD_FAST                0 (key)
            722 BINARY_OP                0 (+)
            726 LOAD_CONST               3 (16)
            728 PRECALL                  2
            732 CALL                     2
            742 BINARY_OP               12 (^)
            746 PRECALL                  1
            750 CALL                     1
            760 PRECALL                  1
            764 CALL                     1
            774 LOAD_METHOD              6 (replace)
            796 LOAD_CONST               2 ('0x')
            798 LOAD_CONST               4 ('')
            800 PRECALL                  2
            804 CALL                     2
            814 STORE_FAST               3 (wdb_key)

 21         816 LOAD_GLOBAL             17 (NULL + print)
            828 LOAD_FAST                3 (wdb_key)
            830 PRECALL                  1
            834 CALL                     1
            844 POP_TOP

 22         846 LOAD_FAST                3 (wdb_key)
            848 RETURN_VALUE

magic_key:7a107ecf29325423
encrypted_data:f2c85bd042247896b43345e589e3ad025fba1770e4ac0d274c1f7c2a670830379195aa5547d78bcee7ae649bc3b914da

‍

我们从
key_encode
函数源码第11行（字节码第一列是源码行号）开始看：

Disassembly of <code object key_encode at 0x14e048a00, file "make.py", line 10>:
 10           0 RESUME                   0

 11           2 LOAD_GLOBAL              1 (NULL + list)
             14 LOAD_FAST                0 (key)
             16 PRECALL                  1
             20 CALL                     1
             30 STORE_FAST               1 (magic_key)

第十行是定义
key_encode
函数，
LOAD_GLOBAL
加载内置list函数，
LOAD_FAST
加载key参数，
PRECALL
准备调用list函数，参数数量为一，
CALL
执行函数调用，

STORE_FAST
将结果存储在局部变量magic_key中。所以源码就是:

magic_key = list(key)

然后我们看源码第12行：

12          32 LOAD_GLOBAL              3 (NULL + range)
             44 LOAD_CONST               1 (1)
             46 LOAD_GLOBAL              5 (NULL + len)
             58 LOAD_FAST                1 (magic_key)
             60 PRECALL                  1
             64 CALL                     1
             74 PRECALL                  2
             78 CALL                     2
             88 GET_ITER
        >>   90 FOR_ITER               105 (to 302)
             92 STORE_FAST               2 (i)

前四行
LOAD_GLOBAL
、
LOAD_CONST
、
LOAD_FAST
分别将range、1、len、magic_key压入栈中，即加载，第一组
PRECALL
和
CALL
是调用len计算magic_key的长度，第二组
PRECALL
和
CALL
是调用range，
GET_ITER、FOR_ITER
开始循环，直到地址302结束，
STORE_FAST
将栈顶弹出存入变量 i 中。所以源码为：

magic_key = list(key)
for i in range(1,len(magic_key)):

然后我们看源码第13行：

 13          94 LOAD_GLOBAL              7 (NULL + str)
            106 LOAD_GLOBAL              9 (NULL + hex)
            118 LOAD_GLOBAL             11 (NULL + int)
            130 LOAD_CONST               2 ('0x')
            132 LOAD_FAST                1 (magic_key)
            134 LOAD_FAST                2 (i)
            136 BINARY_SUBSCR
            146 BINARY_OP                0 (+)
            150 LOAD_CONST               3 (16)
            152 PRECALL                  2
            156 CALL                     2
            166 LOAD_GLOBAL             11 (NULL + int)
            178 LOAD_CONST               2 ('0x')
            180 LOAD_FAST                1 (magic_key)
            182 LOAD_FAST                2 (i)
            184 LOAD_CONST               1 (1)
            186 BINARY_OP               10 (-)
            190 BINARY_SUBSCR
            200 BINARY_OP                0 (+)
            204 LOAD_CONST               3 (16)
            206 PRECALL                  2
            210 CALL                     2
            220 BINARY_OP               12 (^)
            224 PRECALL                  1
            228 CALL                     1
            238 PRECALL                  1
            242 CALL                     1
            252 LOAD_METHOD              6 (replace)
            274 LOAD_CONST               2 ('0x')
            276 LOAD_CONST               4 ('')
            278 PRECALL                  2
            282 CALL                     2
            292 LOAD_FAST                1 (magic_key)
            294 LOAD_FAST                2 (i)
            296 STORE_SUBSCR
            300 JUMP_BACKWARD          106 (to 90)

LOAD_GLOBAL
、
LOAD_CONST
、
LOAD_FAST
分别将全局常量str、hex、int压栈，常量'0x'压栈，变量magic_key和 i 压栈，
BINARY_SUBSCR
索引动作，即magic_key[i]，
BINARY_OP
执行+操作，
LOAD_CONST
将常量16压栈，
PRECALL
和
CALL
执行函数调用，在这里我们先暂停一下，强调一下：
因为是不断的面向栈操作，我们还原源码时一定要和进栈的顺序对应上
，所以我们此时可以还原
int('0x'+magic_key[i],16)
，继续往后看，将int、'0x'、magic_key、i、1压栈，
BINARY_OP
执行 - 操作，
BINARY_SUBSCR
索引，即magic_key[i-1]，
LOAD_CONST
将16压栈，
PRECALL
和
CALL
执行函数调用，此时可以还原
int('0x'+magic_key[i-1],16)
，然后
BINARY_OP
执行 ^ 操作，两组
PRECALL
和
CALL
执行函数调用，此时还原到
str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16)))
，
LOAD_METHOD
将方法replace压栈，后面将'0x'和''压栈，然后调用函数，即replace('0x','')，然后将magic_key、i压栈，进行索引存储，所以源码为：

magic_key = list(key)
for i in range(1,len(magic_key)):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')

后面的同理，不再赘叙，第15行、16行：

magic_key = list(key)
for i in range(1,len(magic_key)):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')

for i in range(0,len(key),2):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')

第18行：

magic_key = list(key)
for i in range(1,len(magic_key)):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')

for i in range(0,len(key),2):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')

magic_key = ''.join(magic_key)

第19行：

magic_key = list(key)
for i in range(1,len(magic_key)):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')

for i in range(0,len(key),2):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')

magic_key = ''.join(magic_key)
print(magic_key)

第20行：

magic_key = list(key)
for i in range(1,len(magic_key)):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')

for i in range(0,len(key),2):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')

magic_key = ''.join(magic_key)
print(magic_key)
wdb_key = str(hex(int('0x'+magic_key) ^ int('0x'+key,16))).replace('0x','')

第21行、22行，此时
key_encode
函数结束：

def key_encode(key):
	magic_key = list(key)
	for i in range(1,len(magic_key)):
		magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')

	for i in range(0,len(key),2):
		magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')

	magic_key = ''.join(magic_key)
	print(magic_key)
	wdb_key = str(hex(int('0x'+magic_key) ^ int('0x'+key,16))).replace('0x','')
	print(wdb_key)
	return wdb_key

然后我们看31行：

key = key_encode(key)

第32行：

key = key_encode(key)
if len(key) == 16:

第33行：

key = key_encode(key)
if len(key) == 16:
	encrypted_data = hex(sm4_encode(key,flag))

第34行：

def key_encode(key):
	magic_key = list(key)
	for i in range(1,len(magic_key)):
		magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')

	for i in range(0,len(key),2):
		magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')

	magic_key = ''.join(magic_key)
	print(magic_key)
	wdb_key = str(hex(int('0x'+magic_key) ^ int('0x'+key,16))).replace('0x','')
	print(wdb_key)
	return wdb_key

key = key_encode(key)
if len(key) == 16:
	encrypted_data = hex(sm4_encode(key,flag))
	print(encrypted_data)

至此我们的源码就搓出来了，题目还给了如下信息：

magic_key:7a107ecf29325423
encrypted_data:f2c85bd042247896b43345e589e3ad025fba1770e4ac0d274c1f7c2a670830379195aa5547d78bcee7ae649bc3b914da

分析可知，我们已知
magic_key
和
encrypted_data
，
encrypted_data
是由
flag
经过sm4加密得到的，密钥为
key
，所以我们需要知道
key
,就可以sm4解密得到
flag
，所以我们需要对 key_encode 函数的逻辑进行逆向得到
key
，最后exp如下：

def key_encode(key):
	magic_key = list(key)
	for i in range(1,len(magic_key)):
		magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')

	for i in range(0,len(key),2):
		magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')

	magic_key = ''.join(magic_key)
	# print(magic_key)
	wdb_key = str(hex(int('0x'+magic_key,16) ^ int('0x'+key,16))).replace('0x','')
	# print(wdb_key)
	return wdb_key

magic_key = list("7a107ecf29325423")

for i in range(0,16,2):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i+1],16))).replace('0x','')

for i in range(len(magic_key)-1,0,-1):
	magic_key[i] = str(hex(int('0x'+magic_key[i],16) ^ int('0x'+magic_key[i-1],16))).replace('0x','')

key = "".join(magic_key)
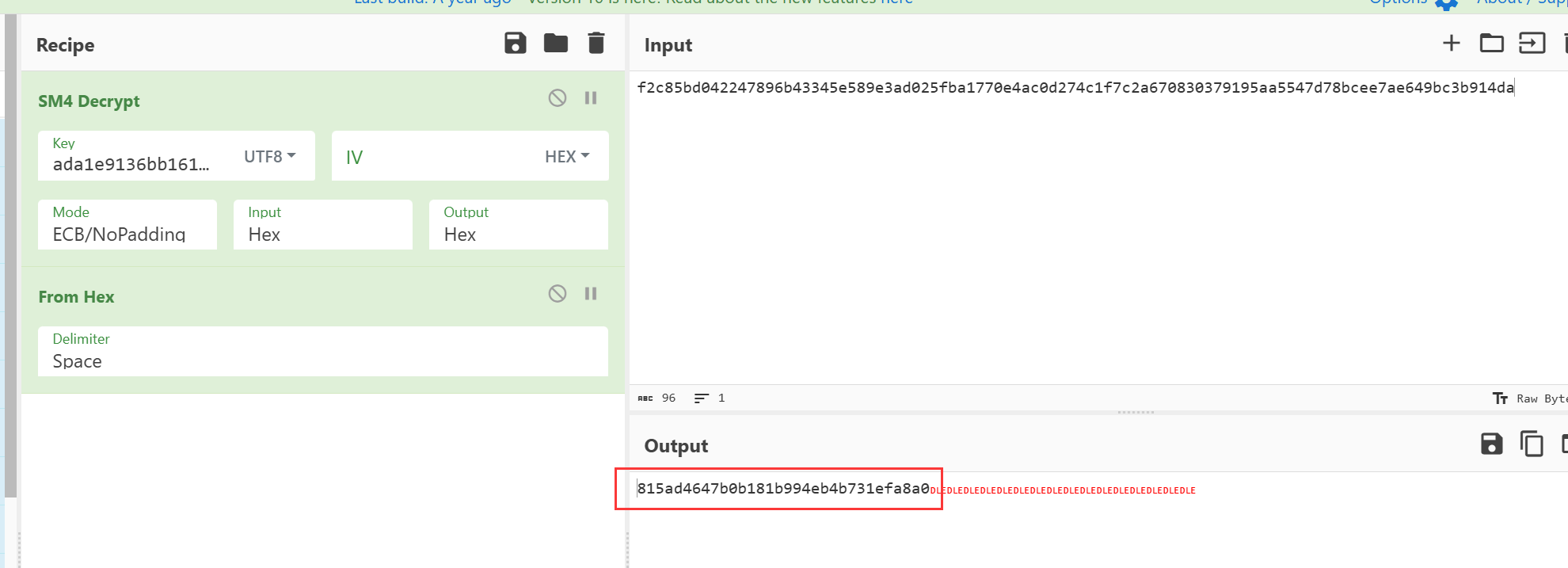
print(key_encode(key))

# 输出：ada1e9136bb16171

然后去赛博厨子解密即可拿到flag：wdflag{815ad4647b0b181b994eb4b731efa8a0}

‍

参考链接：

PyCon 2018：James Bennett--理解 Python 字节码掘金翻译计划
码农高天：字节码和虚拟机？python代码竟然是这么执行的！
王战山的学习笔记：Python中的字节码
python官方文档：dis — Disassembler for Python bytecode

‍

数据结构 - 图

作者: wenmo8
时间: 2024-11-02
分类: 其它
评论

今天我们开始学习目前学习到的最难最复杂的数据结构图。

简单回顾一下之前学习的数据结构，数组、单链表、队列等线性表中数据元素是一对一关系，而树结构中数据元素是一对多关系，而图结构中数据元素则是多对多关系，任何两个数据元素之间都有可能有关系，由此可见图结构的复杂程度。

希望通过这篇文章可以让大家很轻松的了解和学习图结构并快速入门，把一些晦涩难懂概念通过合理的组织归类使其简单明了，再配合一些图例说明，希望可以使大家茅塞顿开。

01
、基础概念

1、定义

图
是一个二元组G=(V(G),E(G))。其中V(G)是非空集，称为
点集
，对于V中的每个元素，我们称其为
顶点
或节点，简称
点
；E(G)为V(G)各节点之间边的集合，称为
边集
。

常用G=(V,E)表示图。

2、组成部分

上面的定义可能较为抽象，我们也可以从另一个角度来理解图，即图的内部结构，图由哪些要素组成的——
点
与
边
。简单来说图就是由若干个点以及连接两点的边构成的图形，而上面的定义也只是在说所有的点和所有的边组成图，这样是不是就很容易理解了。

其中点可以代表某种事物，而边可表示两个事物之间的关系，这样我们就可以把一些实际问题转为图，然后使用软件解决问题。

3、分类

我们可以根据边是否有方向，是否带权，简单的将图分类为无向图、有向图、带权图，当然还有其他类型的图，现阶段我们就不过多介绍了，容易把自己搞晕。

（1）无向图

无向图顾名思义就是
边没有方向
，即两个点之间没有方向，没有顺序之分，这样的边叫作
无向边
，也简称
边
。其中点也叫作
端点
。

（2）有向图

有向图则指
边有方向
，也就代表边所连接的两点有顺序之分，其中一个为
起点
，则另一个则为
终点
，而这样的边就叫作
有向边
或
弧
。起点和终点也叫
端点
。

其中同一个点既可以是起点，也可以是终点。

对于任何图，与一个点关联的所有边数称为该点的
度
。而对于有向图来说，以一个点为起点的边数称为该的点
出度
，以一个点为终点的边数称为该点的
入度
。

如上图点A的出度为3，入度1。

（3）带权图

带权图指每个边都带有一个权重，代表边连接的两点关系的强弱、远近。同时权只是代表边的权重，并不代表边的方向，因此无论无边图还是有边图都可以是带权图。

02
、存储方式

了解了图的基本知识以后，带来了一个新的问题，这么复杂的结构我们要怎么存储下来呢？

下面我们就来介绍几种常用的存储方式邻接矩阵、邻接表、逆邻接表、十字链表。

1、邻接矩阵

邻接矩阵就是用一个二维数组来存储任意两点之间的关系，其中行列索引表示点，而行列索引所在的位置的值表示两点关系，其中两点关系可以用以下数值表示：

（1）
0
：表示两点之间没有边；

（2）
1
：表示两点之间有边；

（3）
权值
：表示两点之间边的权值；

如果图存在n个点，则可以用n x n的二维数组来表示图，下面我们来看看常见图的表示方式。

（1）无向图

对于无向图，如果点A与点B有边，则[A,B]与[B,A]都为1，否则都为0，因此无向图的邻接矩阵是对称的，如下图：

（2）有向图

对于有向图，则可以通过把行索引当作边的起点，把列当作边的终点，来表示方向，比如[A,B]为1，而[B,A]为0，如下图：

对于有向图，我们可以发现关于点的度有以下特性：

点的
出度
就是第i行元素之和；

点的
入度
就是第i列元素之和；

点的
度
就是第i行元素之和 + 第i列元素之和；

（3）带权图

对于带权图，本质上和无向图与有向图相同，只是存储的值有所差别，如果两点之间有边则直接存权值，如果两点之间无边则存一个特殊值（如0、无穷），如果可以保证权值中不存在0,可以用0，否则要选一个其他特殊值，如下图：

总结

优点
：

（1）
简单直观
：实现简单，易于理解，尤其适合小型图。

（2）
快速查找
：便于判断两点之间是否有边，以及各点的度。

缺点
：

（1）
空间浪费
：空间复杂度高为O(n^2)，对于稀疏图，许多元素为零，造成空间浪费。

（2）
不易扩展
：不便于插入和删除点，需要更新整个矩阵，时间复杂度高为O(n)。

2、邻接表

对于邻接矩阵空间浪费以及不易扩展的问题，发展出了另一种链式存储方式——「邻接表」。

邻接表的存储思想和前面章节介绍的散列的链式存储很像。首先我们用一个数组存储所有的点，而每个点元素又作为单链表头，其后继节点则存储与头节点相邻的点元素。

（1）无向图

如下图，图中所有点都存储在数组中，而与其相邻的点存储在其后面的链表中。

点A相邻的点为点B和点C;

点C相邻的点为点A、点D和点E；

点D相邻的点为点C；

（2）有向图

与无向图不同的是有向图链表中存储的不是所有相邻的点，而是存储有方向的点，即以数组中的点为起的终点元素。

点A为起点的终点为点B和点C；

点B为起点的终点为点E；

点D为起点的终点不存在；

通过上图可以发现，邻接表对于有向图可以很直观的表示出某个点的出度，但是对于入度获取就很麻烦。

（3）带权图

带权图与无向图和有向图相比，只需要在元素中多加一个权重属性即可。

总结

优点
：

（1）
节省空间
：时间复杂度相对较低为O(m+n)，m为点数量，n为边数量，对于稀疏图存储效率更高；

（2）
操作灵活
：插入和删除点操作方便，时间复杂度为O(1)；

（3）
出度易取
：对于有向图获取某个点的出度非常方便，只需要找到这个点所在的数组元素位置，然后获取其链表中的元素个数即可；

缺点
：

（1）
不便查找
：判断两点之间是否有边的时间复杂度为O(V), 其中V 是该点的相邻点数量；

（2）
入度难算
：对于有向图点的入度的计算难度较大，时间复杂度为 O(E)，其中E是图中的边的数量；

3、逆邻接表

逆邻接表从名字上就可以看出来和邻接表是逆的关系，这个逆就体现在入度和出度上。我们知道邻接表计算出度容易，计算入度难，而逆邻接表恰恰相反是计算入度容易，计算出度难。

如下图数组中存储点元素，而链表中存储的是以数组中的点为终点的起点元素。

点A为终点的起点不存在；

点B为终点的起点为点A；

点D为终点的起点为点A和点E；

总结

与邻接表差异在于在存储的方向正好相反，所以入度和出度计算难度正好相反，而其他则完全一样。

4、十字链表

邻接表出度计算容易，逆邻接表入度计算容易，那么有没有一种结构同时计算出度入度都容易呢？答案就是十字链表。

十字链表是邻接表和逆邻接表的结合体，每个点的边通过双向链表存储，同时记录了边的出度和入度。

下面我们详细讲解一下十字链表是怎么得到的。

（1）合并逆邻接表与邻接表

如下图我们之间把逆邻接表和邻接表拼接到一起，得到一个伪十字链表。

之所以称这个结合体为伪十字链表，是因为它虽然同时存储了边的两个方向，解决了出度入度计算问题，但是也引发了新的问题——存储效率低。

从上图不难看出链表中存在严重的重复存储的问题。要解决这个问题，我们先梳理一下我们得到的伪十字链表结构。

（2）链表由存点改存边

首先数组存储所有点，左侧链表存储起点元素集合，右侧链表存储终点元素集合；然后我们想为什么需要两条链表呢？因为一条链表就代表一个方向；

那第一步我们是否可以先解决方向的问题呢？而目前的结构节点只有一个点的信息，显然没有方向性，因此我们需要把链表节点改造成包含两个点的结构即起点和终点，这也意味着链表由原来存储点元素变为存储边元素。

原来点A出度链表存储点B和点C，现在改为存储[A->B]边和[A->C]边。

原来点B入度链表存储点A，现在改为存储[A->B]边。

如下图：

（3）删除重复元素

到这里就有条件解决重复的元素的问题了，比如上面链表中有两个[A->B]边，如果我们想把点B入度链表中[A->B]边删除，那么我们必须要有一个途径使得点B的入度链表可以和点A的出度链表中[A->B]边链接上。

首先数组元素结构应该至少包含：数据域|入边头节点指针|出边头节点指针；

然后链表节点元素结构应该至少包含：边起点下标|边终点下标|下一个入边节点指针域|下一个出边节点指针域；

下面我们进行去除重复元素，首先表里下出度链表结构，移除现有入度链表，其中入度链表中的元素指向到出度链表中，最后结果如下图：

如上图红色实线箭头表示出度链表，而彩色虚线箭头表示入度链表。

点A为终点的边不存在，点A为起点的边为 [A->B]边和[A->C]边；

点B为终点的边为[A->B]边（即红色1号虚线），点B为起点的边为 [B->E]边；

点C为终点的边为[A->C]边（即绿色2号虚线）和[E->C]边（即绿色3号虚线）,点C为起点的边为[C->D]边；

总结

优点
：

（1）高效存储，适合复杂的有向图，支持快速遍历；

（2）快速计算出度入度；

缺点
：

（1）实现复杂，维护难度高；

注
：测试方法代码以及示例源码都已经上传至代码库，有兴趣的可以看看。
https://gitee.com/hugogoos/Planner

重新认识下：从程序员泥瓦匠到增长黑客子木

作者: wenmo8
时间: 2024-11-02
分类: 其它
评论

Welcome to
子木聊出海
! 从「程序员泥瓦匠」写技术博客，现在改到「子木聊出海」写一写以下相关的，欢迎阅读和交流～

一、关于我

我是子木，10 年的 SaaS、营销、电商和 AI 等领域经验，一路从技术开发到产品与增长负责人。在过去的职业生涯中，我的工作经历跨越了从编写代码、产品研发、到驱动增长的不同领域，尤其专注于工具类产品的设计、推广和用户增长策略

二、我的职业旅程：从技术，到产品，再到增长驱动产品

我的职业生涯起步于代码开发，那时我主要负责后端架构，追求高效和稳定的技术方案。在有赞工作的那几年，我不仅参与了搜索中台的核心开发，还在增长和市场拓展方面积累了丰富的经验。在担任高级工程师和增长工程师期间，我致力于通过数据和技术手段推动产品增长，例如构建关键词挖掘系统、优化 SEO 策略。我逐渐意识到，增长黑客和 Marketing Research 等可以成为市场营销和用户增长的强大支撑

之后，我走上了产品和增长的道路，先后负责过多个创新产品。两家 SaaS 公司作为业务线负责人，我主导了产品架构、市场定位和用户体验等环节。在这些项目中，我特别注重通过用户需求调研和数据分析来驱动产品迭代

三、现阶段的工作：专注出海与创新

目前，我的工作重心是出海 SaaS，特别是在 AI 视频生成和编辑工具领域。我和组内小伙伴在通过精准的 Google SEO 策略、社交媒体推广、红人营销和 Target Growth 策略，实现了用户和市场一定的增长。目前还在路上，需要我进一步对产品价值的理解，然后逐步扩展到用户需求的深层次挖掘和增长策略的制定

四、我相信的理念 & 个人愿景

我的工作理念可以概括为三点：
技术创新驱动产品价值
、
用户需求定义产品方向
、和
数据分析指导增长决策
。我注重细节并追求结果导向，每一个项目都力求将用户需求与产品设计完美结合，从而创造出能够解决真实问题的产品。

我对技术保持热情，同时希望通过更加市场导向的思维将这些技术应用到实际中去。这种双重背景赋予了我从细节出发、从数据入手制定增长策略的优势，也让在出海 SaaS 这条路上很 Enjoy

未来十年，继续出海软件方向深耕，尤其现阶段结合 AI 技术方向，希望留一些“小作品”在全球市场上。如果你对 AI、产品增长、出海市场感兴趣，或是有相关合作机会，欢迎交流和联系我！

from ：
https://bysocket.com/hello-world/

出处：子木聊出海
博客：bysocket.com
我是子木，爱分享 Learning by Writing. 专注于出海 SaaS，探索 SEO、红人营销、Ads、EDM 等增长策略

【填算符】（log 值域的做法）

作者: wenmo8
时间: 2024-11-02
分类: 其它
评论

比赛在这里呢

填算符

~~下发题解说的神马东西，赛时根本想不到~~

讲一个赛时想得到的
$O(n\log 值域)$
的思路，很好理解

我们处理出二进制下每一位上的 1 的最后一次出现的位置，
将第
$i\ (i\in[0,60])$
位上的 1 最后一次出现的位置记作
$pos_i$

同时我们设
$H=n-k-1$
为总共有的
bitor
的操作数

有以下结论：由于
$pos_i$
是
$i$
位上最后一个 1，所以一旦它后面放了一个与，这一位上就是 0 了；若我们想要这一位为 1，必须至少满足从
$pos_i$
到最后的运算符全是
bitor
。

发现有以下情况：

若
$n-pos_i>H$
，即
$pos_i$
之后需要放的运算符的数量比
bitor
的总操作数多，也就是说在
$pos_i$
之后我一定需要放
bitand
操作，所以这种情况下这一位一定不对答案有贡献
若
$n-pos_i<H$
，也就是说我可以从
$pos_i$
的前一个位置开始到最后全放
bitor
操作，那么这样第
$i$
位上可以是 1，为了使值最大，所以第
$i$
位上一定要是 1，所以从第
$pos_i$
位到最后必须全是
bitor
操作，
对于这种情况的
$i$
我们记为合法位
若
$n-pos_i=H$
，也就是说从第
$pos_i$
到最后的运算符可以全是
bitor
操作，但
$pos_i$
的前一位只能是
bitand
所以我们
特判从第 1 个位置到
$pos_i$
的前一位全放
bitand
能不能让到第
$pos_i$
个数时得到的值第 $\forall $
$j 满足 [pos_j=pos_i]$
位为 1，若能则该位也为合法位，否则不合法

对于所有合法位的
$pos$
取最小值设为
$end$
，因为已经保证
$end$
到最后的预算符全是
bitor
，此时有一下两种可能，而我们想尽量构成第二种可能：

$end$
的前一位预算符也为
bitor
，这样我们一定能达到答案最大了
，想使答案最优直接让从
$end-2$
开始的
$k$
个运算符为
bitor
就好了
$end$
的前一位在某些情况为
bitand
也是可以使答案最大的，所以我们
判断能不能让
$end$
的前一位为
bitand
同样使答案最大；
发现可以的条件相当于从第
$end-1$
个数到最前面用仅剩的
bitor
操作得到一个答案，使得这个答案第 $\forall $
$i 满足 [pos_i=end]$
位为 1，若能满足条件则第
$end-1$
个操作符为
bitand
。

满足条件的判断又和上述的第三个情况判断一致了，相当于以
$end-1$
为下界，再做一次求
$min(合法的\ pos)$
，实质上是不断的递归。

所以一个递归
$dfs(end, H)$
表示下界为
$end$
，还剩
$H$
个
bitor
操作，判断能不能得到我想要的答案：

若不能则直接从第
$end-2$
开始的
$k-res$
个运算符全为
bitand
就是答案（
$res$
为在之前的递归中已经确定的
bitand
的个数）

若能
则第
$end-1$
个位置可以为
bitand
，并设
$end'=min(这一层中合法的\ pos)$
，
继续递归
$dfs(end',H-(end-end'))$
判断第
$end'-1$
个位置能不能为
bitand
。

形式化如下：

搞人工智能开源大语言模型GPT2、Llama的正确姿势

作者: wenmo8
时间: 2024-11-02
分类: 其它
评论

（如果想及时收到人工智能相关的知识更新，请点击关注！！）

序言：
目前我们每一小节的内容都讲解得非常慢，因为这是人工智能研发中的最基础知识。如果我们不能扎实掌握这些知识，将很难理解后续更复杂且实用的概念。因此，我们甚至采用一个概念一节的方式来编排内容，区分得清清楚楚、明明白白，以便大家能够非常明确地了解各知识点之间的关联关系和界限。本节将讲述一种在人工智能领域中被视为“泰斗绝学”的方法，帮助我们高效地完成模型训练——这项绝学就是“迁移学习”。

迁移学习

正如我们在本章中已经看到的那样，使用卷积操作来提取特征是识别图像内容的一个强大工具。生成的特征图可以输入到神经网络的密集层中，与标签匹配，从而更准确地确定图像的内容。通过这种方法，结合一个简单、易于训练的神经网络和一些图像增强技术，我们构建了一个模型，在非常小的数据集上训练时，能够以80-90%的准确率区分马和人。

但是我们可以通过一种叫做迁移学习的方法进一步改进我们的模型。迁移学习的理念很简单：与其从零开始为我们的数据集学习一组滤波器，为什么不使用一个在更大数据集上学习到的滤波器集合呢？该数据集包含了比我们自己“从零开始构建”所能负担得起的更多特征。我们可以将这些滤波器放入我们的网络中，然后使用这些预学习的滤波器训练一个适合我们数据的模型。例如，我们的马或人数据集只有两个类别，而我们可以使用一个已经为一千个类别预训练过的现有模型，但到某个阶段我们不得不舍弃部分已有的网络结构，添加适合两分类的层来构建分类器。

图 3-14 展示了类似于我们这种分类任务的卷积神经网络架构。我们有一系列的卷积层，连接到一个密集层，进而连接到输出层。

                                  图 3-14. 卷积神经网络架构

我们已经看到，使用这种架构，我们能够构建一个相当不错的分类器。但是，通过迁移学习，如果我们可以从另一个模型中提取预学习的层，冻结或锁定它们以使其不可训练，然后将它们置于我们的模型之上，就像图 3-15 所示，这会怎么样呢？

                                        图 3-15. 通过迁移学习从另一个架构中获取层

当我们考虑到，一旦这些层被训练好，它们实际上只是一些数字，表示滤波器的值、权重和偏置，配合一个已知的架构（每层滤波器的数量、滤波器的大小等），那么重用它们的想法就非常直接了当了。

让我们看看代码中的实现。这方面有很多预训练的模型可以使用。我们将使用来自谷歌的流行模型Inception的第3版，它在一个名为ImageNet的数据库中用超过一百万张图片进行了训练。该模型有几十层，可以将图像分类为一千个类别。一个包含预训练权重的已保存模型也已经可以使用。要使用它，我们只需下载这些权重，创建一个Inception V3架构的实例，然后将这些权重加载到这个架构中，代码如下：

from tensorflow.keras.applications.inception_v3 import InceptionV3

weights_url = "
https://storage.googleapis.com/mledudatasets/inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5
"

weights_file = "inception_v3.h5"

urllib.request.urlretrieve(weights_url, weights_file)

pre_trained_model = InceptionV3(input_shape=(150, 150, 3),

include_top=False,

weights=None)

pre_trained_model.load_weights(weights_file)

现在我们有一个完整的预训练Inception模型。如果你想查看它的架构，可以用以下代码：

pre_trained_model.summary()

不过要小心，它很庞大！可以浏览一下，看看层和它们的名称。我喜欢用一个叫做mixed7的层，因为它的输出很小——7 × 7的图像——不过你可以随意尝试其他层。

接下来，我们将冻结整个网络，使其不再重新训练，然后设置一个变量指向mixed7的输出，作为我们要裁剪网络的位置。代码如下：

for layer in pre_trained_model.layers:

layer.trainable = False

last_layer = pre_trained_model.get_layer('mixed7')

print('last layer output shape: ', last_layer.output_shape)

last_output = last_layer.output

注意，我们打印了最后一层的输出形状，你会看到我们在这时得到了7 × 7的图像。这表示当图像被传递到mixed7时，滤波器输出的图像大小为7 × 7，所以很容易管理。同样，你不必选择这个特定层，可以尝试其他层。

现在让我们看看如何在这个输出下添加我们的密集层：

/
将输出层展开为1维
/

x = layers.Flatten()(last_output)

/
添加一个带有1,024个隐藏单元和ReLU激活的全连接层
/

x = layers.Dense(1024, activation='relu')(x)

/
添加一个用于分类的最终sigmoid层
/

x = layers.Dense(1, activation='sigmoid')(x)

就这么简单，我们将最后的输出展平，因为我们将把结果传递到密集层中。然后，我们添加一个包含1,024个神经元的密集层，和一个带有1个神经元的输出层。

现在我们可以简单地将模型定义为预训练模型的输入，接着是刚刚定义的x，然后以通常的方式编译它：

model = Model(pre_trained_model.input, x)

model.compile(optimizer=RMSprop(lr=0.0001),

loss='binary_crossentropy',

metrics=['acc'])

在这个架构上训练模型40个周期后，准确率达到99%+，验证准确率则达到96%+（见图3-16）。

                                图 3-16. 使用迁移学习训练马或人分类器

这里的结果比我们之前的模型要好得多，但你可以继续进行微调和改进。你还可以试试这个模型在更大数据集上的表现，比如Kaggle上著名的猫狗大战（Dogs vs. Cats）。这是一个非常多样化的数据集，包含了25,000张猫和狗的图片，很多图片中的主体都有一定遮挡——比如被人抱着的情况下。

使用之前的同样算法和模型设计，你可以在Colab上训练一个猫狗分类器，利用GPU每个周期大约3分钟。训练20个周期，大约需要1小时。

在测试一些非常复杂的图片时（如图3-17所示），这个分类器全都判断正确。我特意选择了一张长着像猫耳朵的狗的图片，还有一张背对着的狗的图片。另外两张猫的图片也都是非典型的。

                                    图 3-17. 成功分类的非典型猫狗图片

右下角的那只猫，闭着眼睛、耳朵下垂、伸着舌头舔爪子，把它加载到模型中时，得到了图3-18中的结果。你可以看到，它给出了一个非常低的值（4.98 × 10⁻²⁴），这表明网络几乎可以确定它是一只猫！

                                    图 3-18. 分类舔爪子的猫

你可以在作者的一个GitHub仓库中找到马或人分类器以及猫狗分类器的完整代码。

本节我们介绍了使用“迁移学习”的方法来完成模型训练，省去了繁琐的前期训练过程，通过迁移已有知识并结合少量数据进行微调即可实现模型的适应性。这种方法是通用的，适用于小型神经网络，同样也适用于如2024年Facebook的开源大型语言模型Llama等知名大模型。在这些预训练模型的基础上，迁移学习可以有效节省大量GPU资源的预训练成本。下一节我们要讲解的也是人工智能模型训练中的很重要的技能“随机失活”法。

2024年11月