MViT:性能杠杠的多尺度ViT | ICCV 2021
论文提出了多尺度视觉
Transformer
模型
MViT
,将多尺度层级特征的基本概念与
Transformer
模型联系起来,在逐层扩展特征复杂度同时降低特征的分辨率。在视频识别和图像分类的任务中,
MViT
均优于单尺度的
ViT
。来源:晓飞的算法工程笔记 公众号
论文: Multiscale Vision Transformers

Introduction
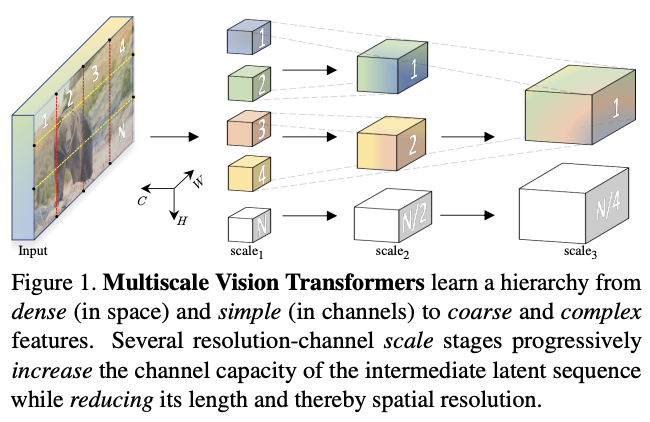
论文提出了用于视频和图像识别的多尺度ViT(
MViT
),将
FPN
的多尺度层级特征结构与
Transformer
联系起来。
MViT
包含几个不同分辨率和通道数的
stage
,从小通道的输入分辨率开始,逐层地扩大通道数以及降低分辨率,形成多尺度的特征金字塔。
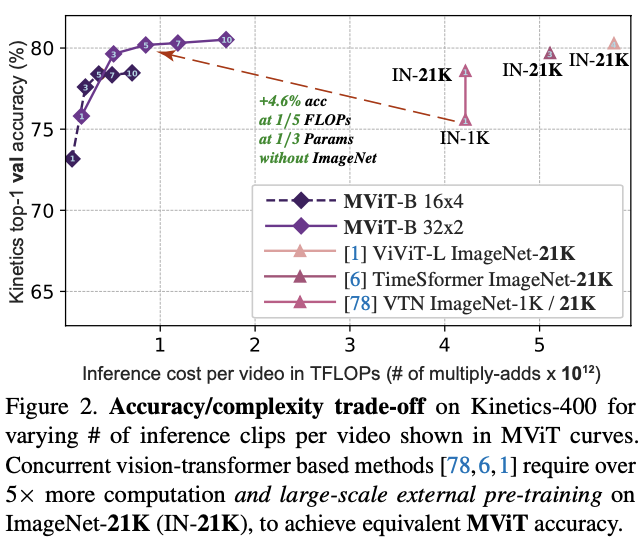
在视频识别任务上,不使用任何外部预训练数据,
MViT
比视频
Transformer
模型有显着的性能提升。而在
ImageNet
图像分类任务上,简单地删除一些时间相关的通道后,
MViT
比用于图像识别的单尺度ViT的显着增益。
Multiscale Vision Transformer (MViT)
通用多尺度
Transformer
架构的核心在于多
stage
的设计,每个
stage
由多个具有特定分辨率和通道数的
Transformer block
组成。多尺度
Transformers
逐步扩大通道容量,同时逐步池化从输入到输出的分辨率。
Multi Head Pooling Attention
多头池化注意(
MHPA
)是一种自注意操作,可以在
Transformer block
中实现分辨率灵活的建模,使得多尺度
Transformer
可在逐渐变化的分辨率下运行。与通道和分辨率固定的原始多头注意(
MHA
)操作相比,
MHPA
池化通过降低张量的分辨率来缩减输入的整体序列长度。
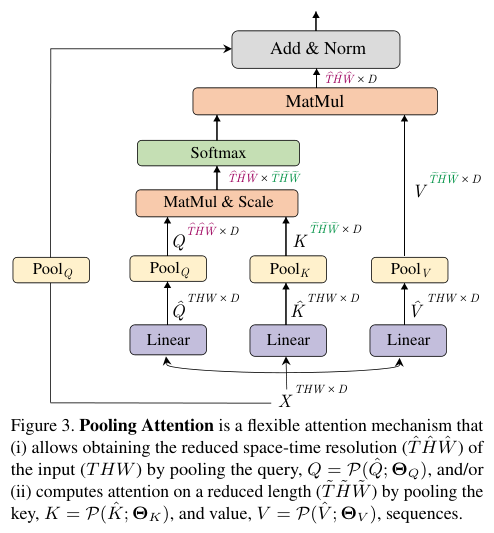
对于序列长度为
\(L\)
的
\(D\)
维输入张量
\(X\)
,
\(X \in \mathbb{R}^{L\times D}\)
,根据
MHA
的定义先通过线性运算将输入
\(X\)
映射为
Query
张量
\(\hat{Q} \in \mathbb{R}^{L\times D}\)
,
Key
张量
\(\hat{K} \in \mathbb{R}^{L\times D}\)
和
Value
张量
\(\hat{V} \in \mathbb{R}^{L\times D}\)
。
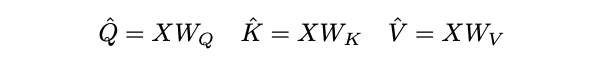
然后通过池化操作
\(\mathcal{P}\)
将上述张量缩减到特定长度。
Pooling Operator
在进行计算之前,中间张量
\(\hat{Q}\)
、
\(\hat{K}\)
、
\(\hat{V}\)
需要经过池化运算
\(\mathcal{P}(·; \Theta)\)
的池化,这是的
MHPA
和
MViT
的基石。
运算符
\(\mathcal{P}(·; \Theta)\)
沿每个通道对输入张量执行池化核计算。将
\(\Theta\)
分解为
\(\Theta := (k, s, p)\)
,运算符使用维度
\(k\)
为
\(k_T\times k_H\times k_W\)
、步幅
\(s\)
为
\(s_T\times s_H \times s_W\)
、填充
\(p\)
为
\(p_T\times p_H\times p_W\)
的池化核
\(k\)
,将维度为
\(L = T\times H\times W\)
的输入张量减少到
\(\tilde{L}\)
:
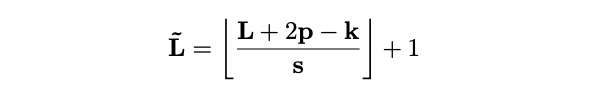
通过坐标公式计算,将池化的张量展开得到输出
\(\mathcal{P}(Y ; \Theta)\in \mathbb{R}^\tilde{L}\times D\)
,序列长度减少为
\(\tilde{L}= \tilde{T}\times \tilde{H}\times \tilde{W}\)
。
默认情况下,
MPHA
的重叠内核
\(k\)
会选择保持形状的填充值
\(p\)
,因此输出张量
\(\mathcal{P}(Y ; \Theta)\)
的序列长度能够降低
\(\tilde{L}\)
整体减少
\(s_{T}s_{H}s_{W}\)
倍。
Pooling Attention.
池化运算符
\(\mathcal{P}(\cdot; \Theta)\)
在所有
\(\hat{Q}\)
、
\(\hat{K}\)
、
\(\hat{V}\)
中间张量中是独立的,使用不同的池化核
\(k\)
、不同的步长
\(s\)
以及不同的填充
\(p\)
。定义
\(\theta\)
产生的池化后
pre-attention
向量为
\(Q = P(\hat{Q}; \Theta_Q)\)
,
\(K = P(\hat{K}; \Theta_K)\)
和
\(V = P(\hat{V}; \Theta_V)\)
,随后在这些向量上进行注意力计算:
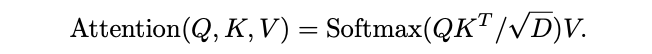
根据矩阵乘积可知,上述公式会引入
\(S_K=S_V\)
的约束。总体而言,池化注意力的完整计算如下:
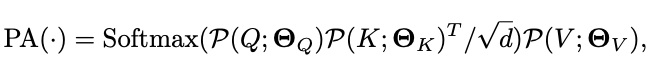
\(\sqrt{d}\)
用于按行归一化内积矩阵。池化注意力计算的输出序列长度的缩减跟
\(\mathcal{P}(\cdot)\)
中的
\(Q\)
向量一样,为步长相关的
\(s^Q_TS^Q_HS^Q_W\)
倍。
Multiple heads.
与常规的注意力操作一样,
MHPA
可通过
\(h\)
个头来并行化计算,将
\(D\)
维输入张量
\(X\)
的平均分成
\(h\)
个非重叠子集,分别执行注意力计算。
Computational Analysis.
Q
、
K
、
V
张量的长度缩减对多尺度
Transformer
模型的基本计算和内存需求具有显着的好处,序列长度缩减可表示为:
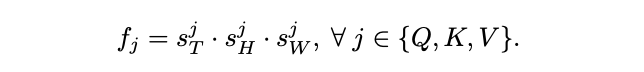
考虑到
\(\mathcal{P}(·; \Theta)\)
的输入张量具有通道
\(D\times T\times H\times W\)
,
MHPA
的每个头的运行时复杂度为
\(O(T HW D/h(D + T HW/f_Q f_K))\)
和内存复杂度为
\(O(T HW h(D/h + T HW/f_Q f_K))\)
。
另外,通过对通道数
\(D\)
和序列长度项
\(THW/f_Q f_K\)
之间的权衡,可指导架构参数的设计选择,例如头数和层宽。
Multiscale Transformer Networks
Preliminaries: Vision Transformer (ViT)
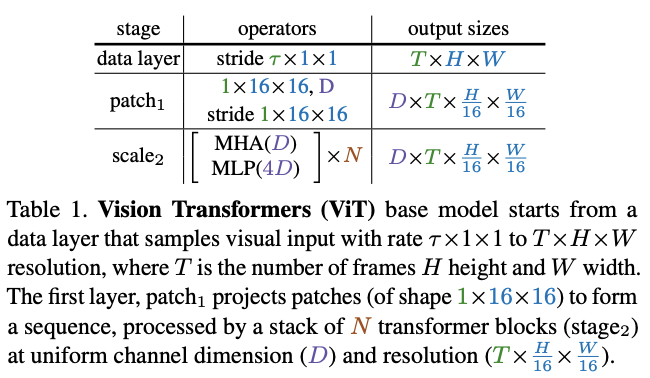
ViT
将
\(T\times H\times W\)
的输入切分成
\(1\times 16\times 16\)
的不重叠小方块,通过
point-wise
的线性变换映射成
\(D\)
维向量。
随后将
positional embedding
\(E\in \mathbb{R}^{L\times D}\)
添加到长度为
\(L\)
、通道为
\(D\)
的投影序列中,对位置信息进行编码以及打破平移不变性。最后,将可学习的
class embedding
附加到投影序列中。
得到的长度为
\(L + 1\)
的序列由
\(N\)
个
Transformer block
依次处理,每个
Transformer block
都包含
MHA
、
MLP
和
LN
操作。定义
\(X\)
视为输入,单个
Transformer block
的输出
\(Block(X)\)
的计算如下:

\(N\)
个连续
block
处理后的结果序列会被层归一化,随后将
class embedding
提取并通过线性层预测所需的输出。默认情况下,
MLP
的隐藏层通道是
\(4D\)
。另外,需要注意的是,
ViT
在所有块中保持恒定的通道数和空间分辨率。
Multiscale Vision Transformers (MViT).
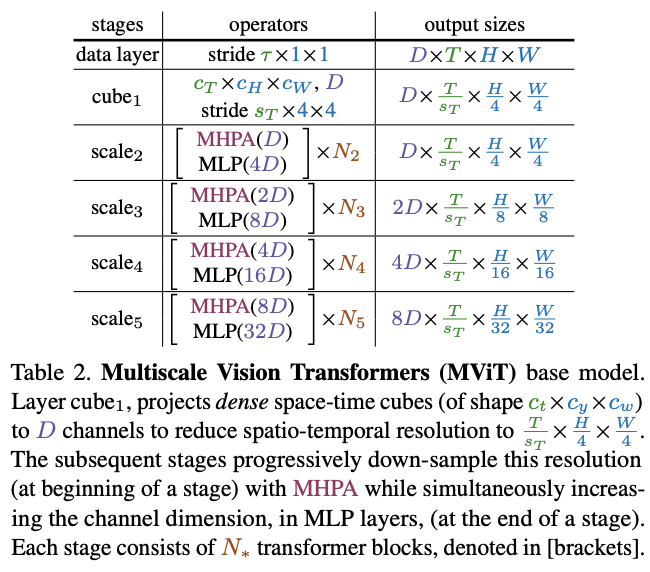
MViT
的关键是逐步提高通道通道以及降低空间分辨率,整体结构如表2所示。
Scale stages
每个
scale stage
包含
\(N\)
个
Transformer block
,
stage
内的
block
输出相同通道数和分辨率的特征。在网络输入处(表2中的
cube1
),通过三维映射将图像处理为通道数较小(比典型的
ViT
模型小8倍),但长度很长(比典型的
ViT
模型高16倍)图像块序列。
在
scale stage
之间转移时,需要上采样处理序列的通道数以及下采样处理序列的长度。这样的做法能够有效地降低视觉数据的空间分辨率,使得网络能够在更复杂的特征中理解被处理的信息。
Channel expansion
在
stage
转移时,通过增加最后一个
MLP
层的输出来增加通道数。通道数的增加与空间分辨率的缩减相关,假设空间分倍率下采样4倍,那通道数则增加2倍。这样的设计能够在一定程度上保持
stage
之间的计算复杂度,跟卷积网络的设计理念类似。
Query pooling
由
MPHA
公式可知,
Q
张量可控制输出的序列长度,通过步长为
\(s\equiv (s^Q_T, s^Q_H, s^Q_W)\)
的
\(\mathcal{P}(Q;k;p;s)\)
池化操作将序列长度缩减
\(s^Q_T\cdot s^Q_H\cdot s^Q_W\)
倍。在每个
stage
中,仅需在开头中减少分辨率,剩余部分均保持分辨率,所以仅设置
stage
的首个
MHPA
操作的步长`
\(S^Q > 1\)
,其余的约束为
\(s^Q\equiv (1,1,1)\)
。
Key-Value pooling
与
Q
张量不同,改变
K
和
V
张量的序列长度不会改变输出序列长度,但在降低池化操作的的整体计算复杂度中起着关键作用。
因此,对
K
、
V
和
Q
池化的使用进行解耦,
Q
池化用于每个
stage
的第一层,
K
、
V
池化用于剩余的层。由
MPHA
公式可知,
K
和
V
张量的序列长度需要相同才能计算注意力权重,因此
K
、
V
张量池化的步长需要相同。在默认设置中,约束同一
stage
的池化参数
\((k; p; s)\)
为相同,即
\(\Theta_K ≡ \Theta_V\)
,但可自适应地改变
stage
之间的
s
缩放参数。
Skip connections
如图3所示,由于通道数和序列长度在
residual block
内发生变化,需要在
skip connection
中添加
\(\mathcal{P}(\cdot; {\Theta}_{Q})\)
池化来适应其两端之间的通道不匹配。
同样地,为了处理
stage
之间的通道数不匹配,采用一个额外的线性层对
MHPA
操作的
layer-normalized
输出进行升维处理。
Network instantiation details

表3展示了
ViT
和
MViT
的基本模型的具体结构:
ViT-Base
(表 3a):将输入映射成尺寸为
\(1\times 16\times 16\)
且通道为
\(D = 768\)
的不重叠图像块,然后使用
\(N = 12\)
个
Transformer block
进行处理。对于
\(8\times 224\times 224\)
的输入,所有层的分辨率固定为
\(768\times 8\times 14\times 14\)
,序列长度为
\(8\times 14\times 14 + 1=1569\)
。MViT-Base
(表 3b):由4个
scale stage
组成,每个
stage
都有几个输出尺寸一致的
Transformer block
。
MViT-B
通过形状为
\(3\times 7\times 7\)
的立方体(类似卷积操作)将输入映射且通道为
\(D = 96\)
的重叠图像块序列,序列长度为
\(8\times 56\times 56 + 1 = 25089\)
。该序列每经过一个
stage
,序列长度都会减少4倍,最终输出的序列长度为
\(8\times 7\times 7 + 1 = 393\)
。同时,通道数也会被上采样2倍,最终增加到768。需要注意,所有池化操作以及分辨率下采样仅在数据序列上执行,不涉及
class token embedding
。
在
scale1 stage
将
MHPA
的头数量设置为
\(h = 1\)
,随着通道数增加头数量(保持
\(D/h=96\)
)。在
stage
转移时,通过
MLP
前一
stage
的输出通道增加2倍,并且在下一
stage
开头对
Q
执行
MHPA
池化,其中
\(s^{Q} = (1, 2, 2)\)
。
在
MHPA block
中使用
\(\Theta_K \equiv \Theta_V\)
的
K
、
V
池化,其中,
scale1
的步长为
\(s^{K}=(1,8,8)\)
。步长随着
stage
的分辨率缩小而减少,使得
K
、
V
在
block
间保持恒定的缩放比例。
Experiments
Video Recognition
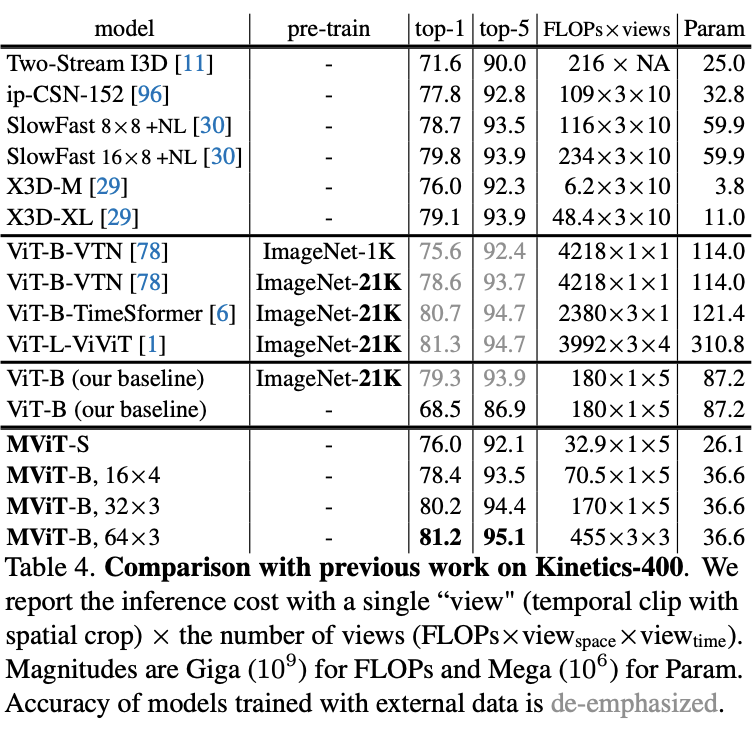
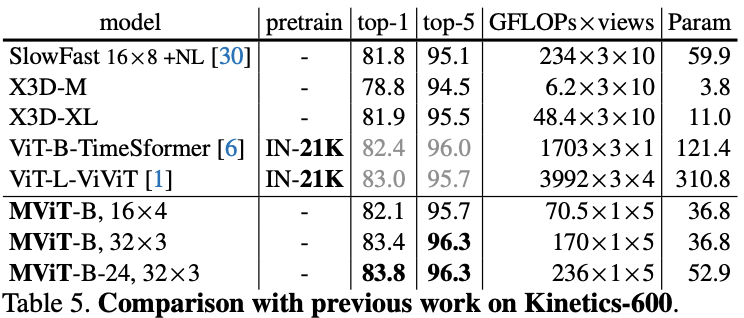
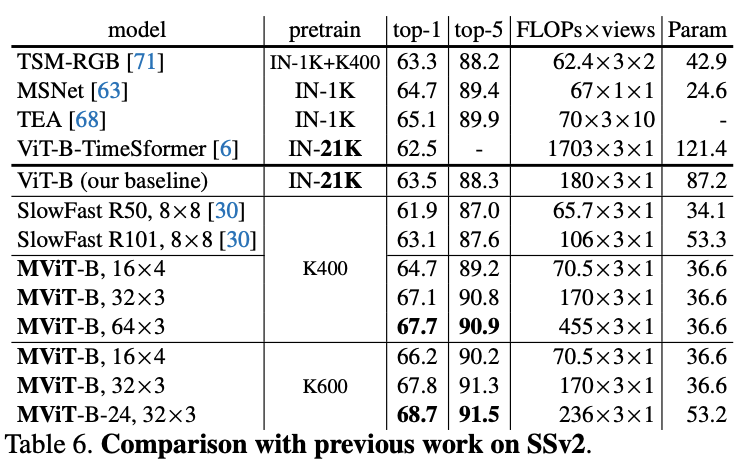

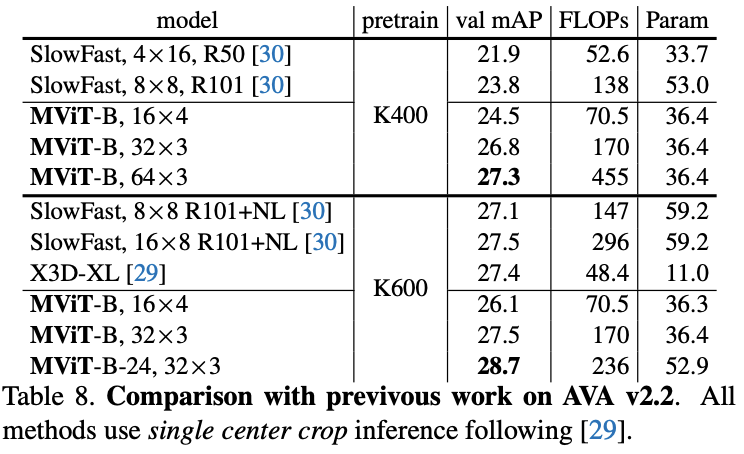
在五个视频识别数据集上的主要结果对比,
MViT
均有不错的性能提升。
Image Recognition
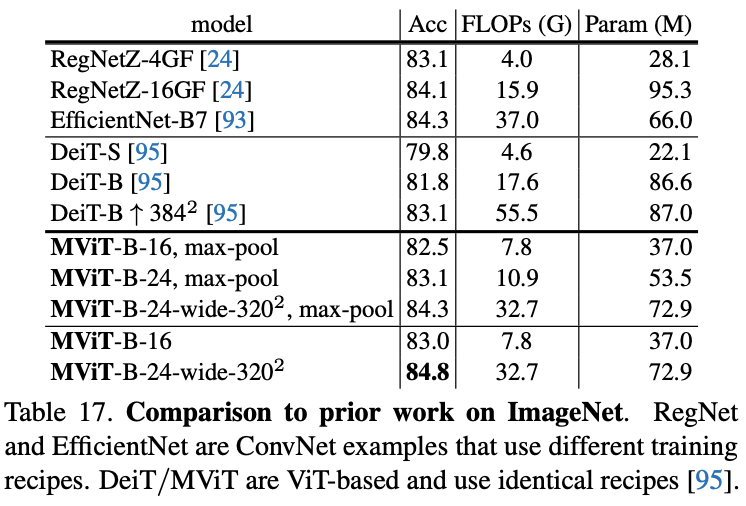
在ImageNet上对比图像分类效果。
Conclusion
论文提出了多尺度视觉
Transformer
模型
MViT
,将多尺度层级特征的基本概念与
Transformer
模型联系起来,在逐层扩展特征复杂度同时降低特征的分辨率。在视频识别和图像分类的任务中,
MViT
均优于单尺度的
ViT
。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
