cmu15545-数据访问方式:B+树(B+Tree)
基本概念
基于磁盘的B+树
为什么使用B+数进行数据访问(Access Method):

- 天然有序,支持范围查找
- 支持遍历所有数据,利用顺序IO
- 时间复杂度为
\(O(logn)\)
,满足性能需求 - 相比于B树,数据访问都在叶子结点:磁盘空间利用率高;并发冲突减少
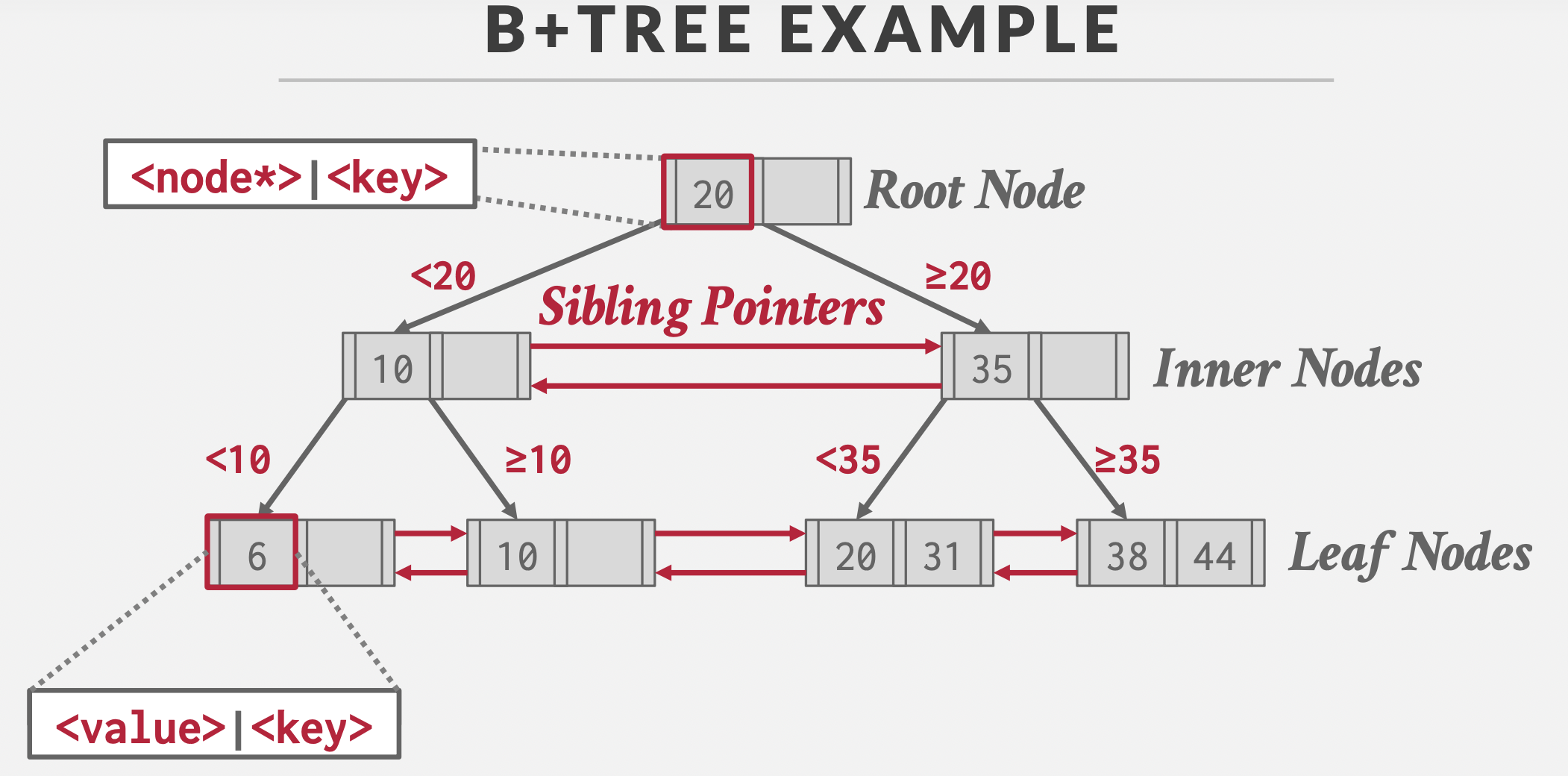
一个基础的B+树:
- 三类借点:根结点,中间结点,叶子结点
- 数据分布:根结点和中间结点只存储索引,叶子结点存储数据
- 指针关系:父子指针,兄弟指针
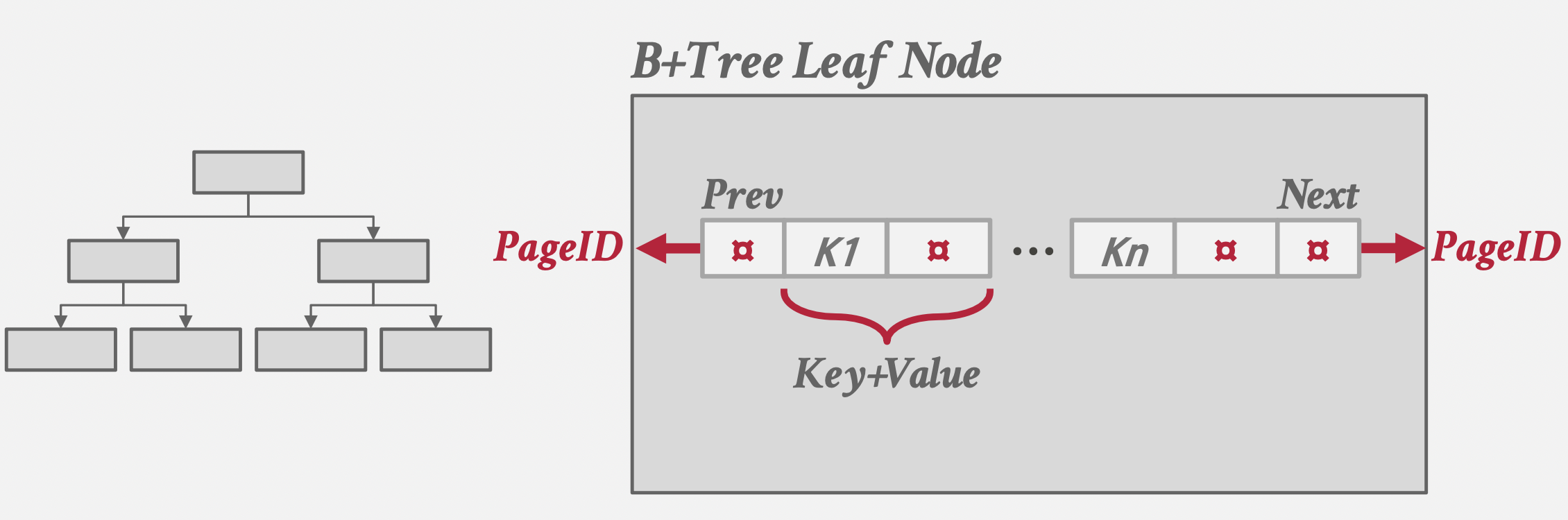
基于磁盘的B+树映象:
一个结点存储在一个堆文件(Heap File)页中;页ID(PageId)代替指针的作用。
键值联合存储
键值分别存储
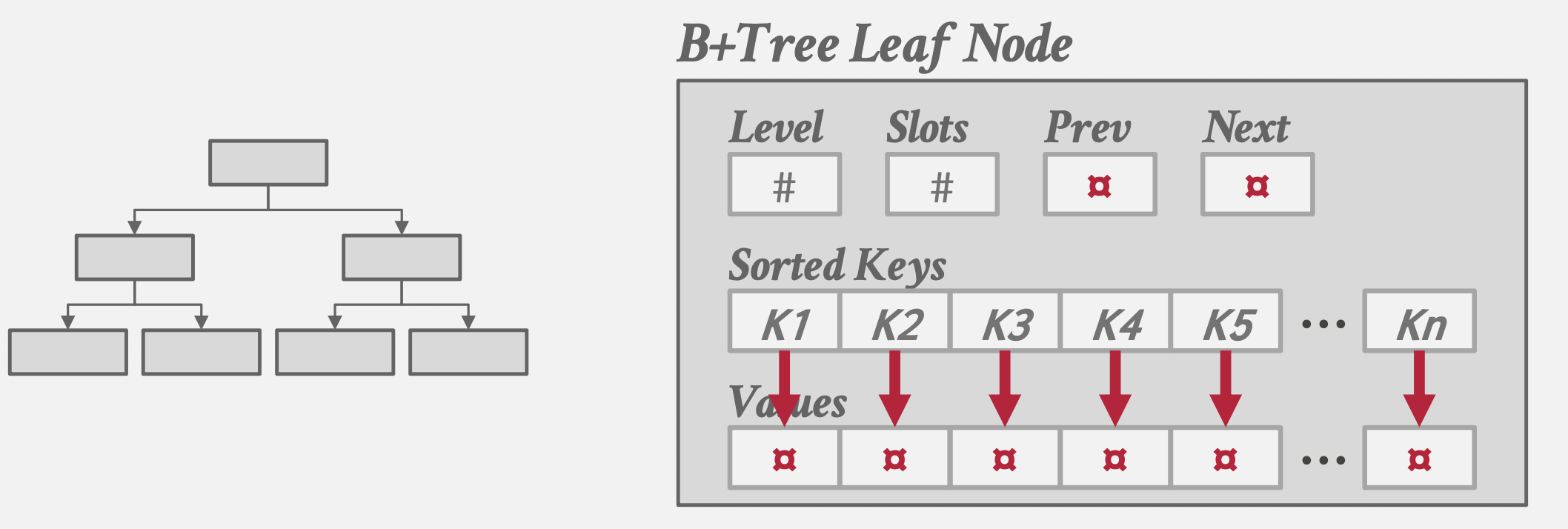
B+树的叶子结点存储实际数据,这个数据如何理解,取决于不同的数据库实现:有些存储RecordID,有些基于索引组织(Index-Organized Storage)的数据库则直接存储元组(Tuple)数据。
如果不了解RecordID,数据组织方式,可以参看
这篇博文
。
查询与索引
最左前缀匹配
有联合索引
<a,b,c>
,支持如下查询条件
(a=1 AND b=2 AND c=3)(a=1 AND b=2)
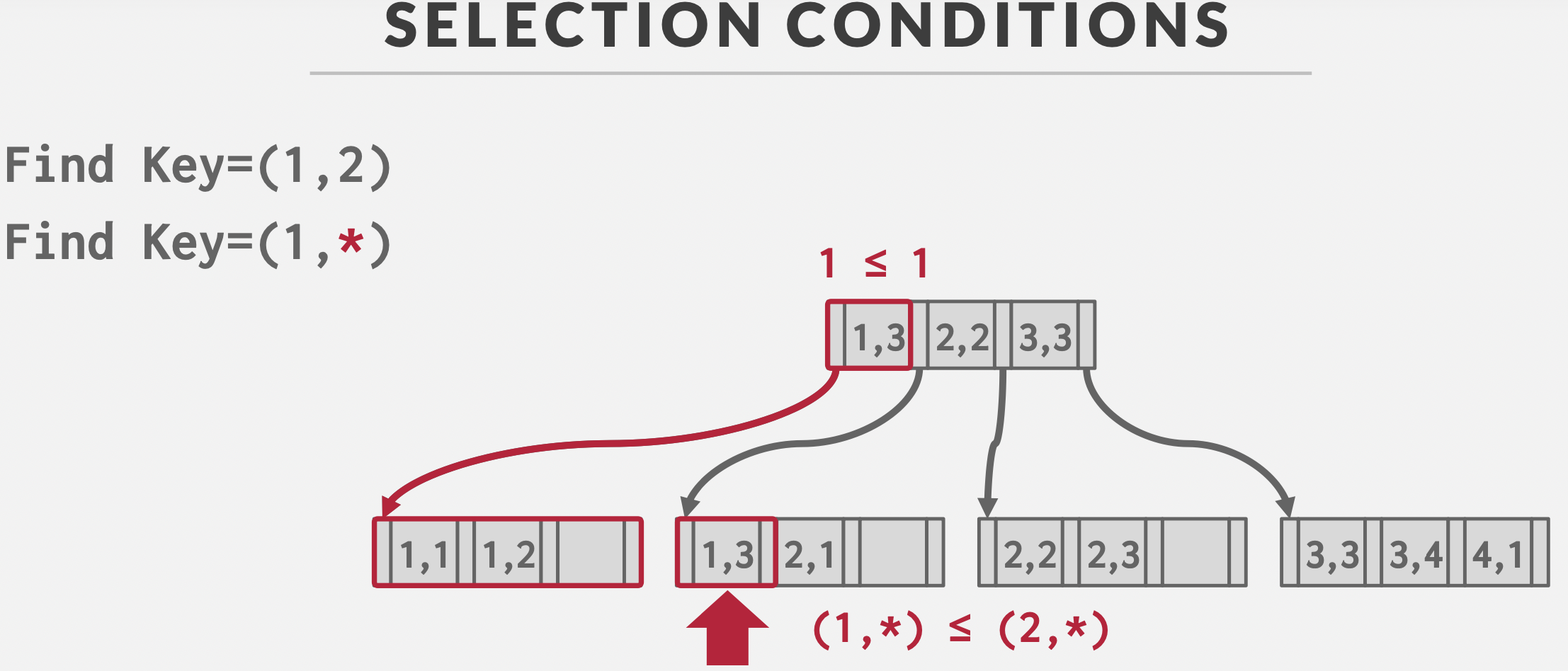
如果所有不满足最左前缀匹配原则,需要全表扫描。
如何处理重复键
加上RecordID使其变成唯一键
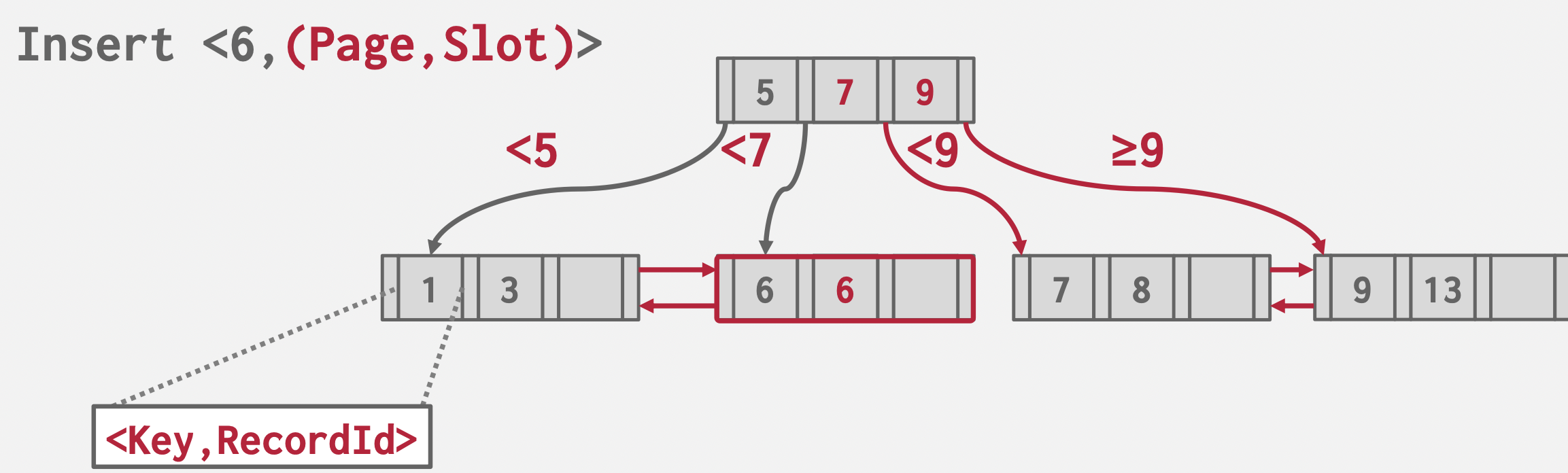
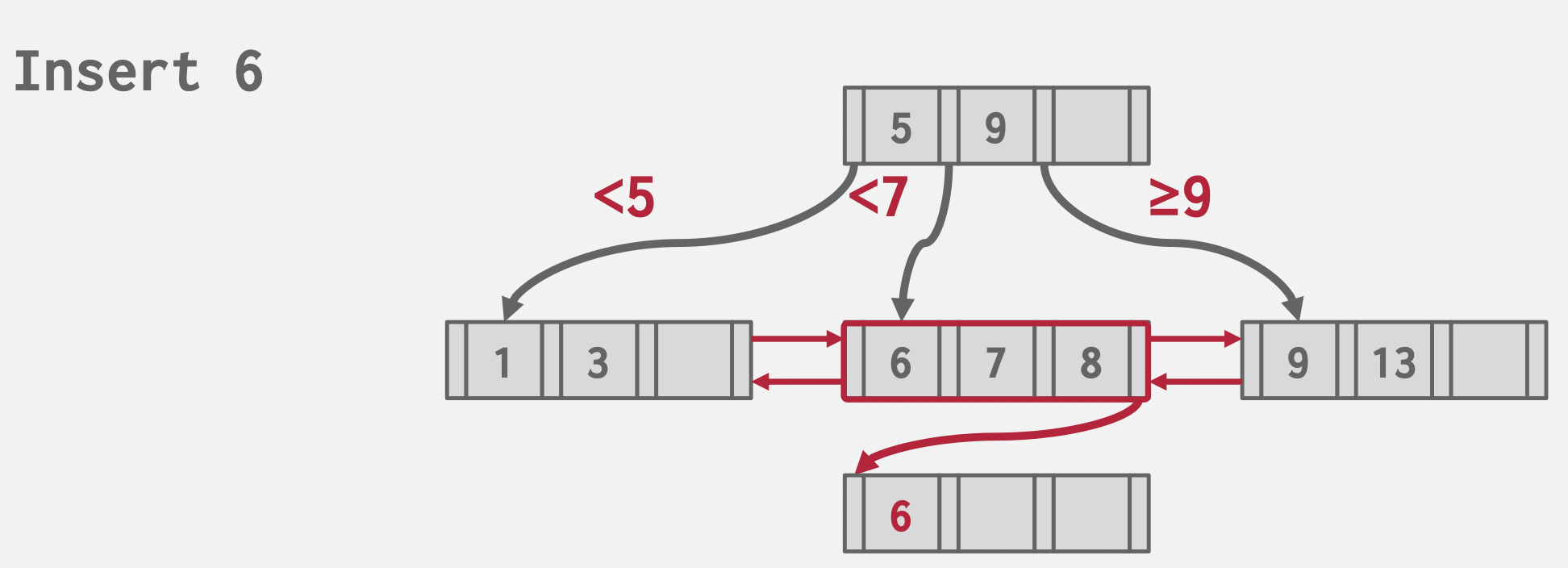
叶子结点溢出(没有实际系统采用)
聚簇索引
- 一个表只能有一个聚簇索引
- 索引键和值存储在一起
- 数据按照索引的键排序
- 操作数据时要同步操作索引
聚簇索引是非必须的,取决于数据库具体实现,Mysql和SQLite中数据直接用聚簇索引组织。
用B+树实现聚簇索引可以很方便地实现范围查询和便利,充分利用顺序IO。

对于非聚簇索引,虽然索引的键有序,但是对应的数据在磁盘上不一定是顺序存储的,所以很有效的方式是先得到PageID,后根据PageID进行排序,最后获取数据,充分利用顺序IO。
设计选择
结点大小(Node Size)
存储设备读取数据越慢,越需要利用顺序IO,结点就越大;
存储设备读取数据越快,越需要减少冗余数据读取,结点就越小。
- HDD:~1MB
- SSD:~10KB
- In-Memory:~512B
合并阈值(Merge Thredshold)
结点中的键数量低于半满的时候,不会立刻进行合并,而是允许小结点存在,然后再周期性地重建整棵树。
PostgreSQL中称其为不平衡的B+树("non-balanced" B+Tree, nbtree)。
变长键(Variable-length Keys)
- 指针:键存储指向实际数据的指针【无法利用顺序IO,因为要跳转去读取指针内容】
- 变长结点
- 填充数据(Padding)
实际系统中的索引数据和堆文件数据一样,是能存结点就存结点中,是在存不下存指针。
结点内部搜索(Intra-Node Search)
线性查找:由于SIMD指令集存在,实际顺序查询,其实可以是批处理
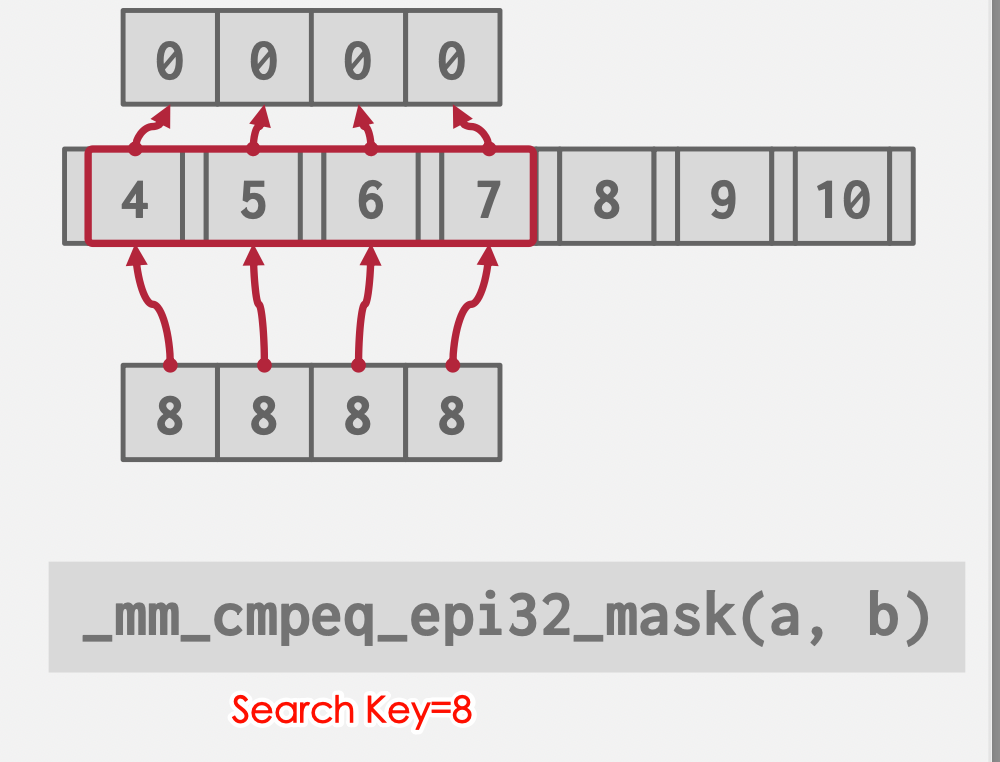
二分查找
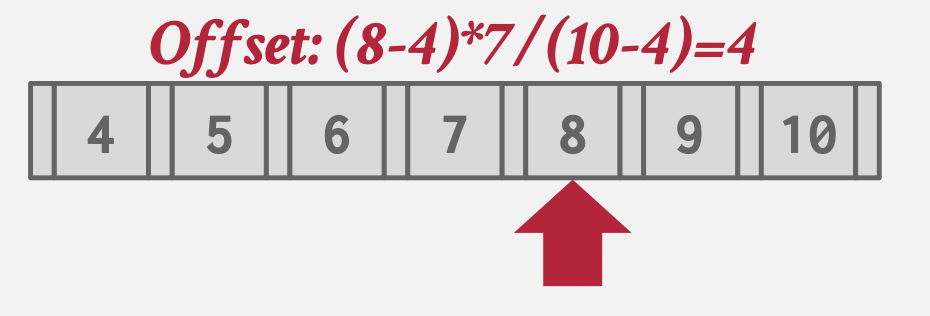
插值法:键没有间隙的时候(自增),可以直接计算出偏移
优化手段
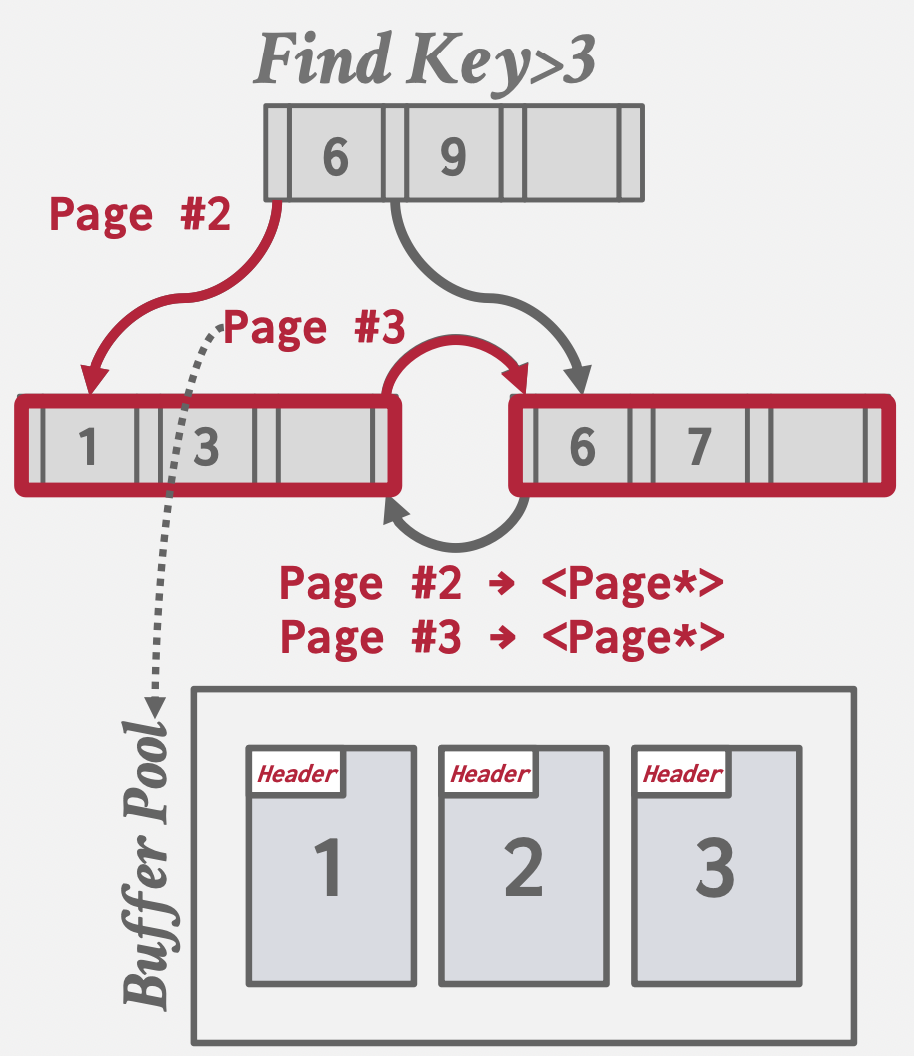
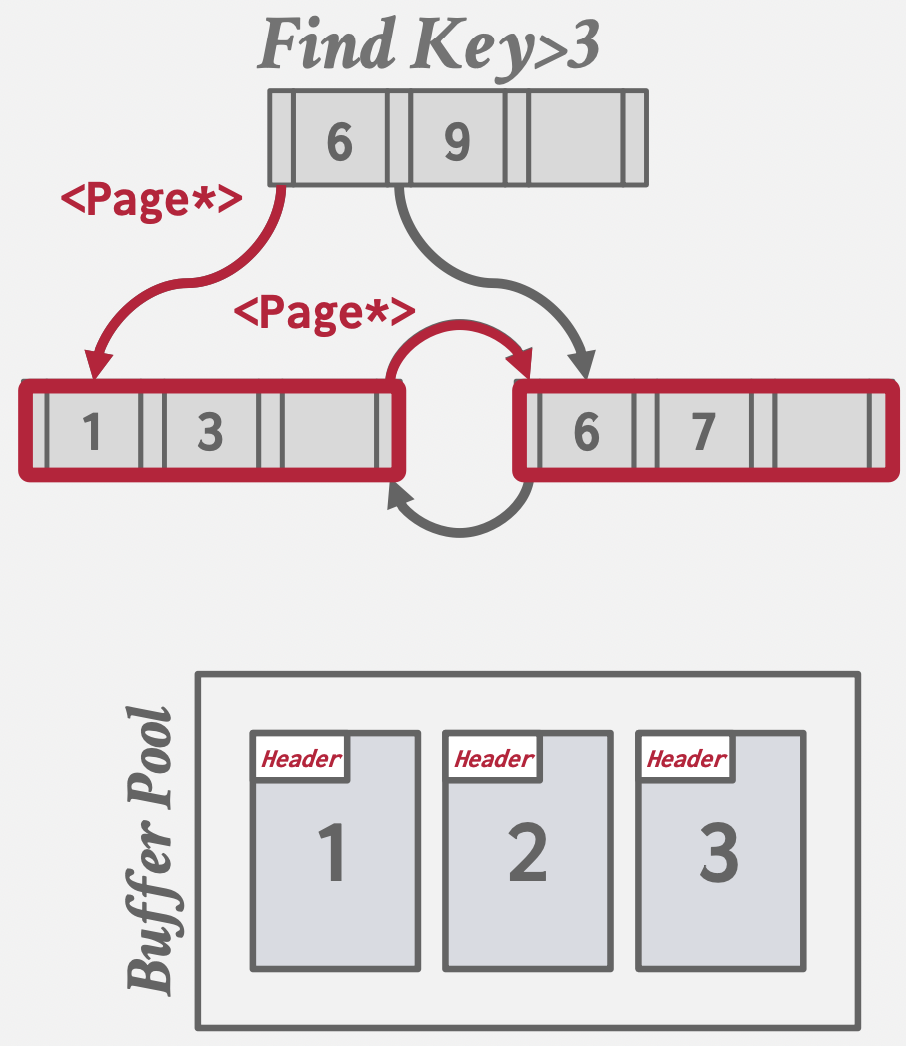
Pointer Swizzling
基本思想:当一个对象从磁盘加载到内存时,将其磁盘地址转换成内存地址(
swizzling
),以便程序在内存中直接通过指针访问。
例子:比如主键索引的B+树根结点读取到Buffer Pool后,会被pin住,不被置换出去,所以此时可以直接用内存指针访问根结点,省略用PageID问Buffer Pool要内存地址的步骤。
图示:
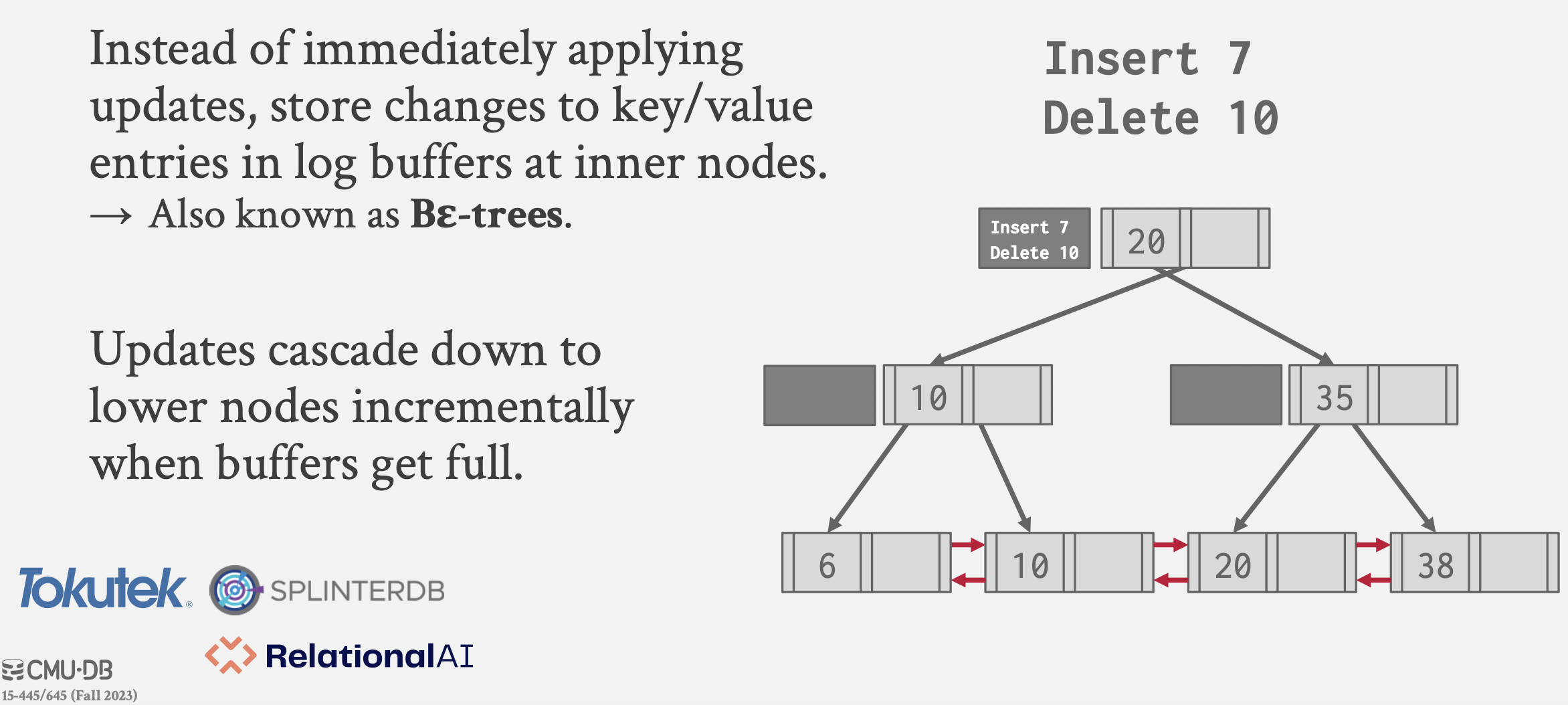
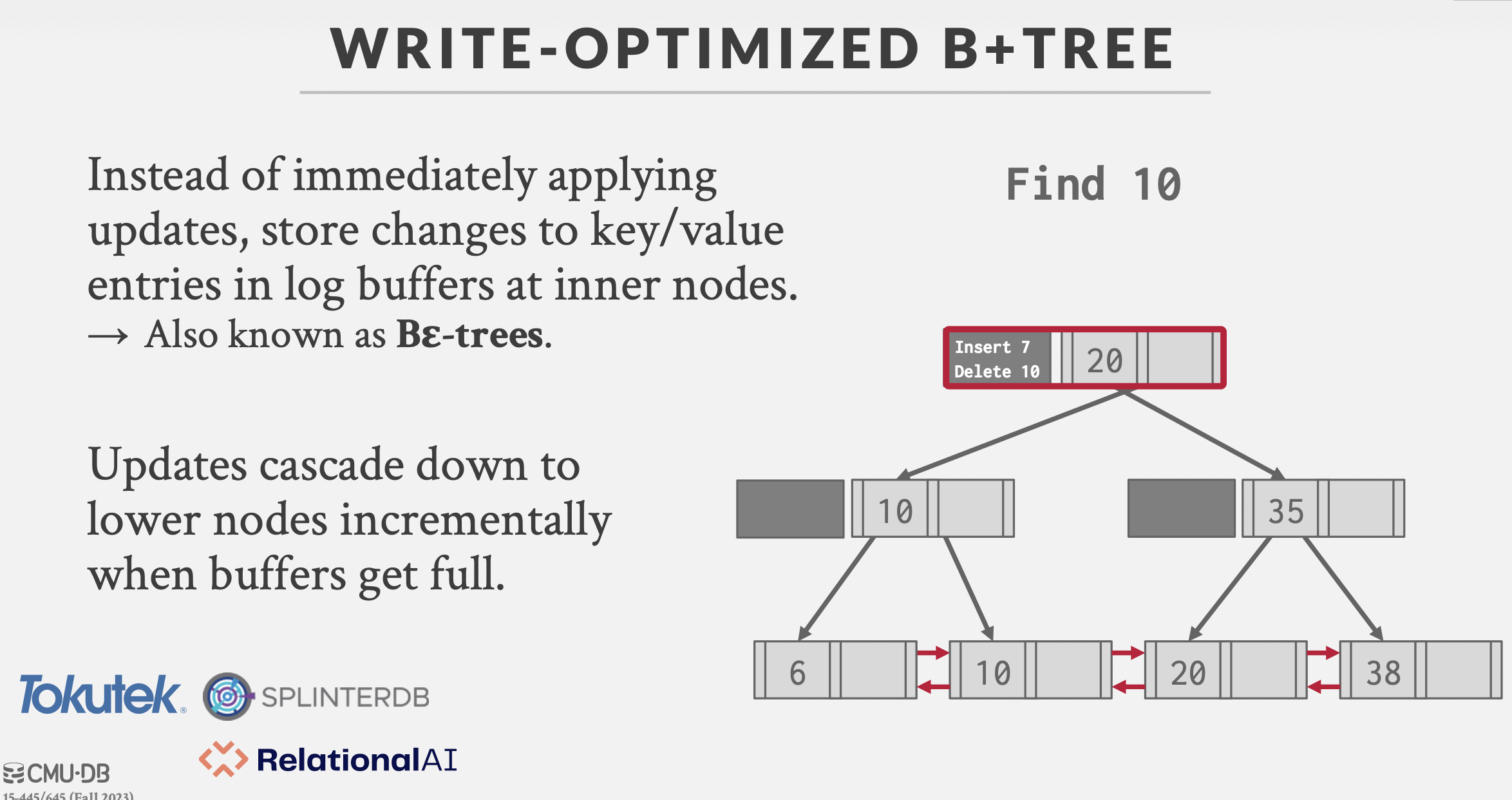
Bε-trees
一种B+树的写优化。
基本思想:更新时不直接修改数据 ,而是记录日志(类似于log-structured data storage)。
日志记录在结点上,当结点日志记录满以后,该结点的日志下推到孩子结点。
Bulk Insert
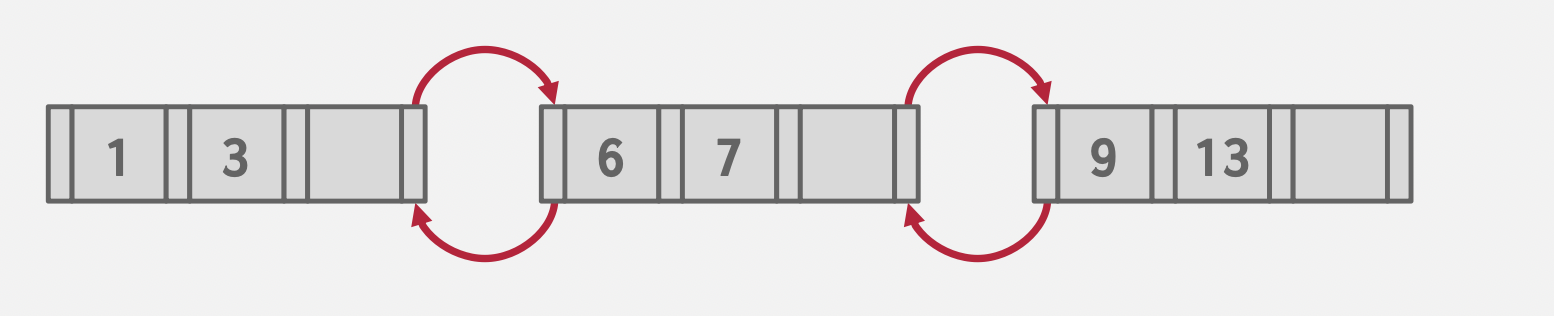
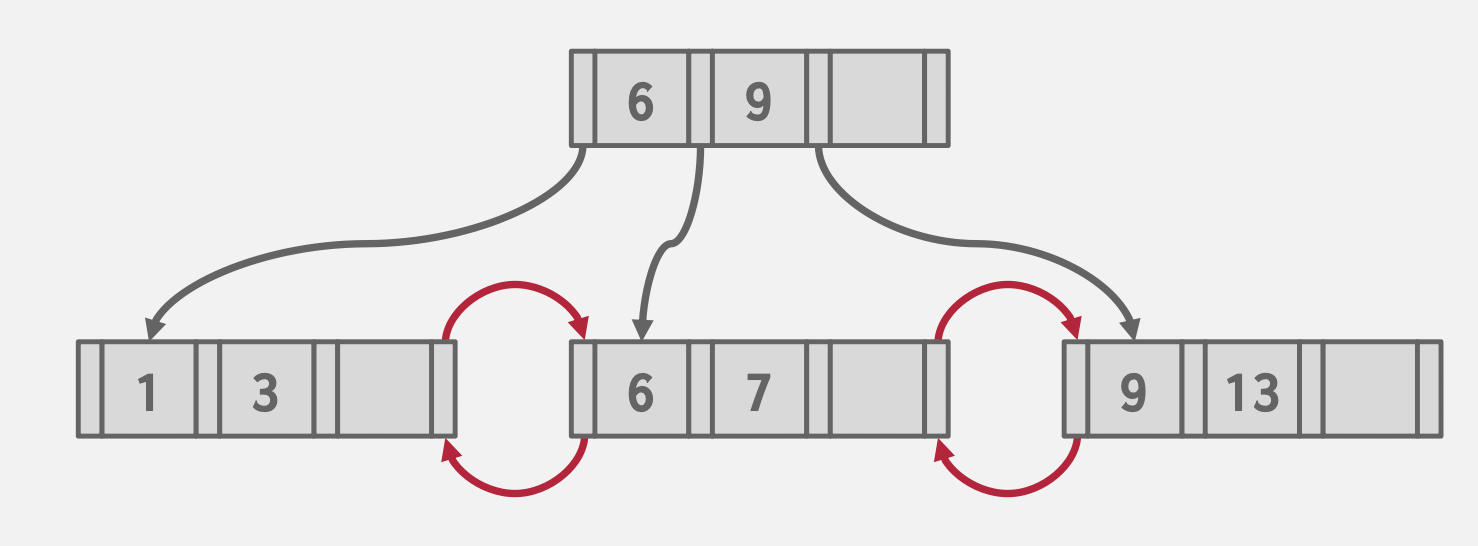
基本思想:由底至顶创建B+树,而不是由顶至底。
减少了插入时树的结构变化,前提是需要预先排序数据。
Keys: 3, 7, 9, 13, 6, 1
Sorted Keys: 1, 3, 6, 7, 9, 13
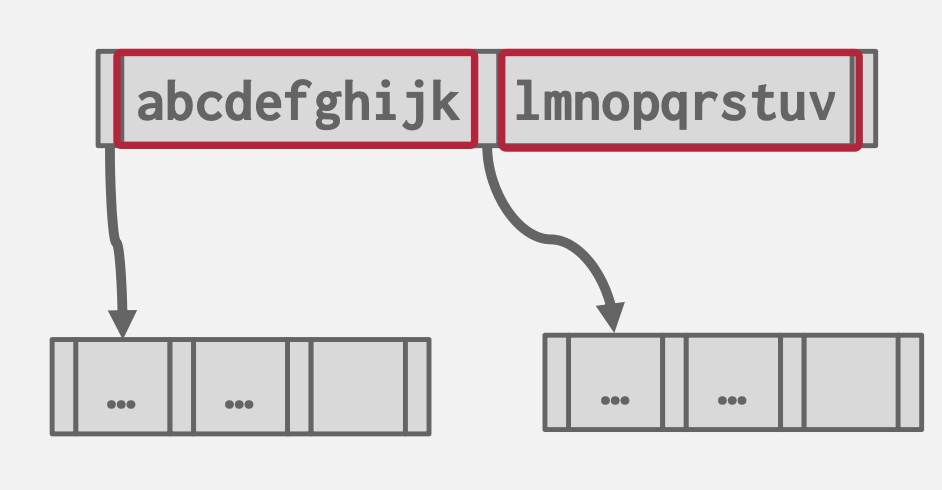
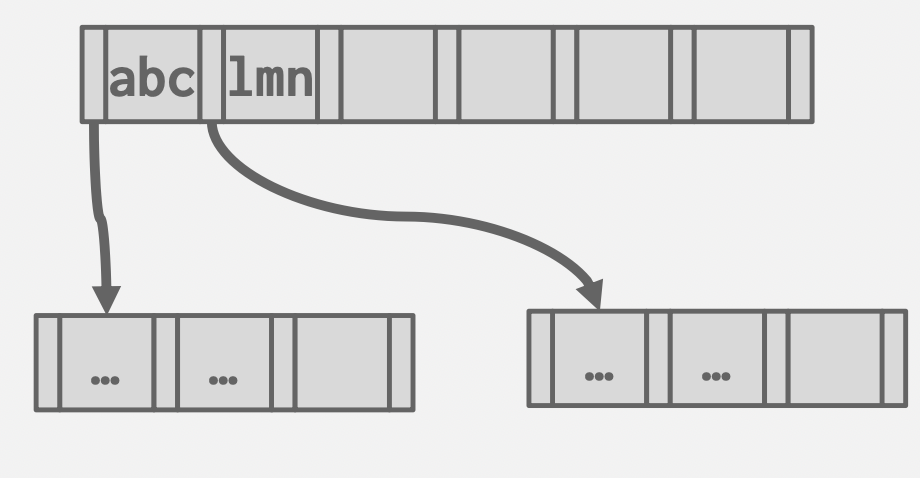
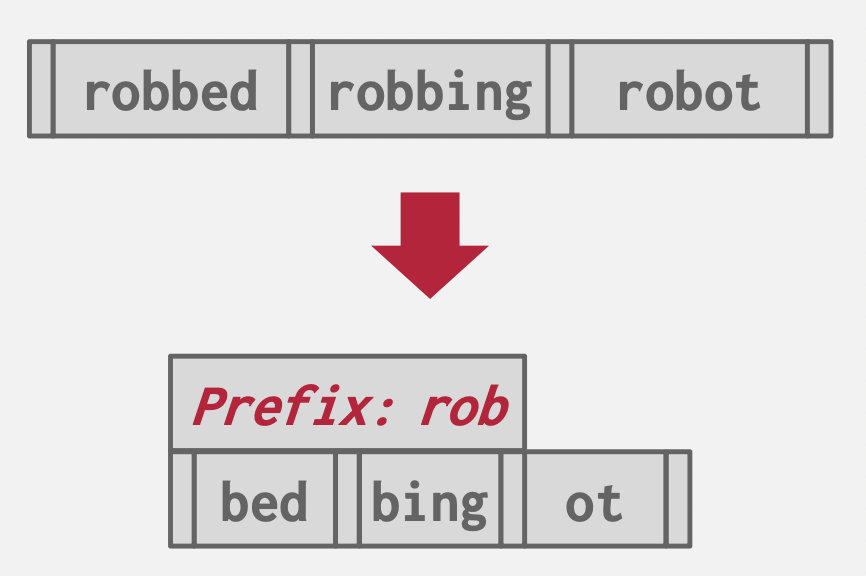
Prefix Compression
基本思想:字典序压缩前缀。
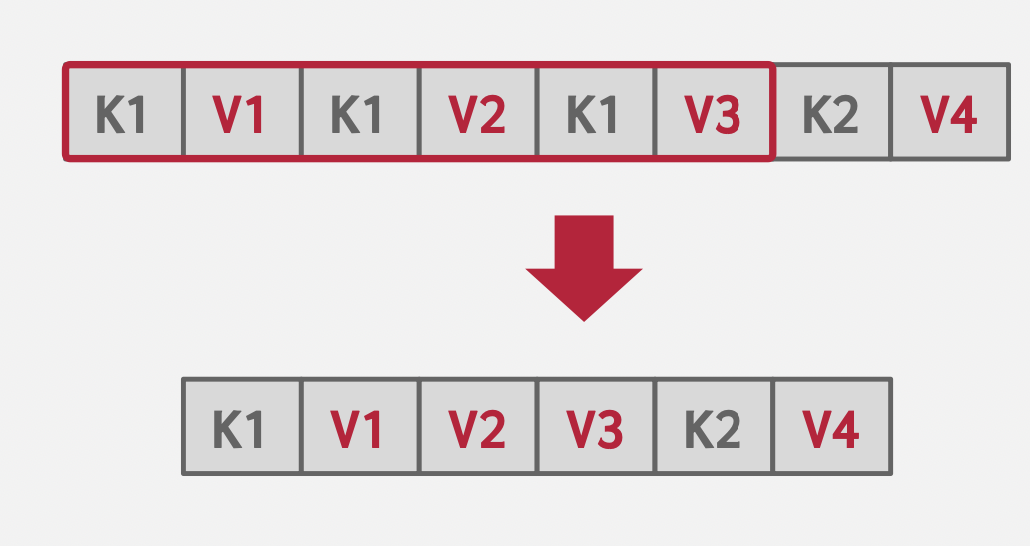
Deduplication
基本思想:非唯一索引中避免重复存储相同键。
Suffix Truncation
基本思想:中间结点只是起引路作用,所以存储能辨识的最小前缀即可。