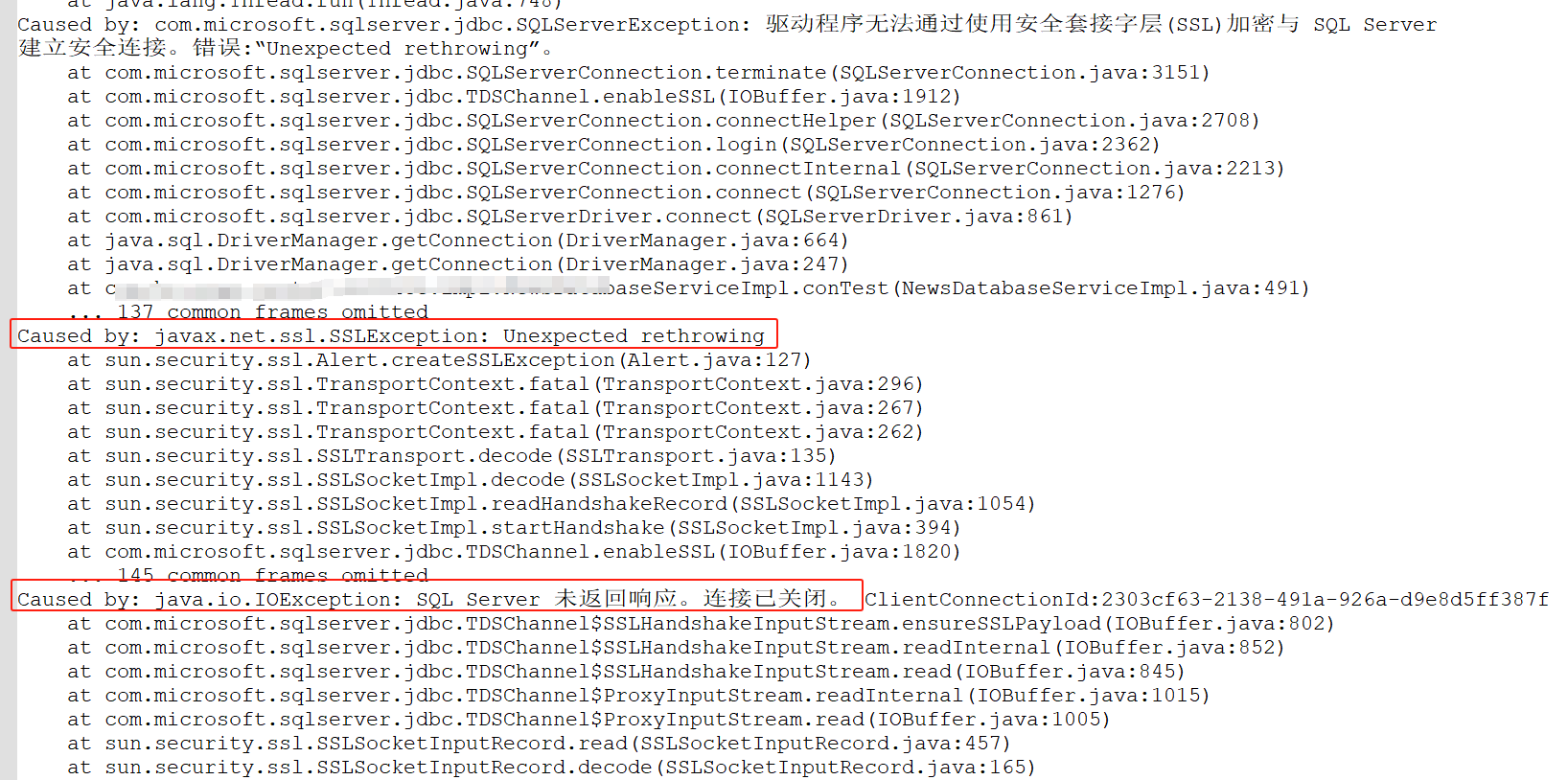
【原创】浅谈EtherCAT主站EOE(下)-EtherCAT IgH主站EoE具体实现
本文介绍了linux内核态EtherCAT主站igh 中EoE的具体实现,希望对你有所帮助。
1.IgH 框架概述
详见本博客博文
【原创】EtherCAT主站IgH解析(一)--主站初始化、状态机与EtherCAT报文
,不再赘述。
2. IgH EOE机制
【原创】浅谈EtherCAT主站EOE(上)-EOE网络
中已经对EOE有了整体的认识,EOE是与操作系统EtherNet相关的,这意味着不同的主站、在不同的操作系统下具体实现是不一样的,接下来我们看看linux内核态中的igh主站EOE是如何实现的。
2.1 EoE服务规范
按照ETG官方文档中对EoE应用服务的定义,EoE主站需要提供如下服务:
- 初始化EoE请求(Initiate EoE),暂不清楚其作用和应用场合。
request:EOE frameType 0x02
response: EOE frameType 0x03
- EoE帧传输请求(EoE Fragment),用于传输主站与从站的标准以太网数据,
只有请求,没有响应。
request:EOE frameType 0x00
- 设置IP参数请求(Set IP Parameter),设置从站的IP地址、网关等配置信息,请求-响应模式。
request:EOE frameType 0x02
response: EOE frameType 0x03
- 设置MAC过滤器请求(Set MAC Filter),请求-响应模式。暂不清楚其作用和应用场合。
request:EOE frameType 0x04
response: EOE frameType 0x05
关于EOE服务的数据结构规范参考ETG100.6.
2.1 EoE虚拟网络设备
首先IgH主站运行在Linux内核态,所以上篇文章
【原创】浅谈EtherCAT主站EOE(上)-EOE网络
中的情况之一。
主站完成从站扫描后,EtherCAT主站根据SII信息中邮箱协议的支持情况,为支持EoE的从站创建虚拟网络设备,注册到linux网络设备驱动中,用于和EoE从站的数据交互,在Linux看来就是多了很多虚拟以太网网卡,每个网络接口对于一个ethercat eoe从站。
2.1.1 EoE Virtual Network Interfaces
创建虚拟网络设备接口时,其接口名称规定如下:
eoe<MASTER>[as]<SLAVE>
[as]
a表示使用别名,
<SLAVE>
则为站点别名;s表示使用别名,
<SLAVE>
则为站点地址,
<MASTER>
表示主站index。
2.1.2 EoE Virtual Network MAC Address
Eoe Mac地址派生自唯一的mac。
现在,EoE MAC地址从可用网络接口的链接列表的第一个全局唯一MAC地址的NIC部分派生,或者从EtherCAT主站使用的MAC地址派生,或者linux随机生成。
EoE MAC地址将采用
02:NIC:NIC:NIC:RP:RP
的格式,其中
NIC
来自唯一的MAC地址,而RP是EoE从站的环位置。
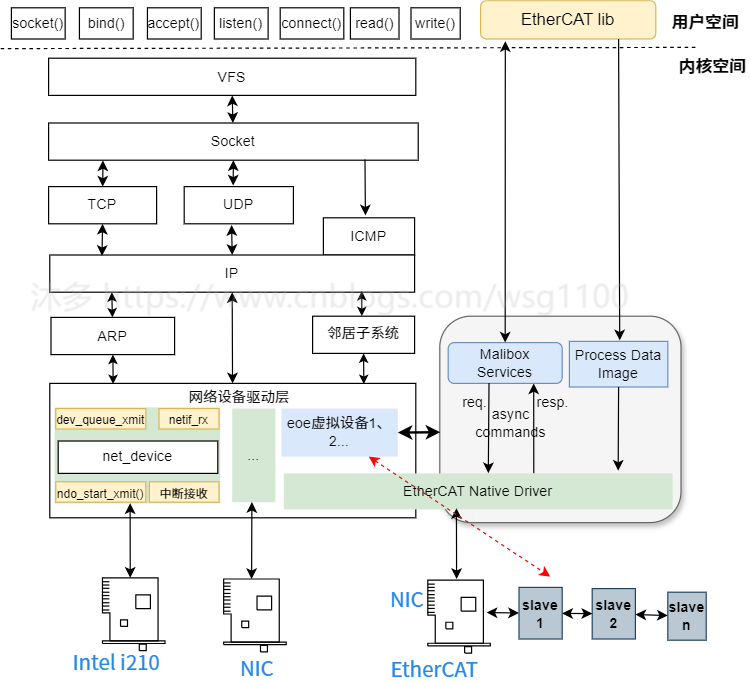
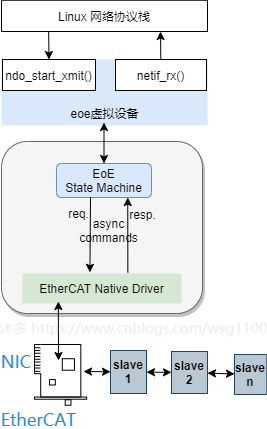
2.2.3 Linux网络数据处理流程
再介绍igh eoe具体实现之前,有必要先介绍Linux网络数据处理,以Linux 应用TCP通信为例,根据上图,简要说明一个网络数据如何到达网络设备驱动层的:
VFS 层:应用通过write socket文件描述符发送数据,
write
系统调用找到
struct file
,根据里面的
file_operations
的定义,调用
sock_write_iter
函数。
sock_write_iter
函数调
sock_sendmsg
函数。Socket 层:从
struct file
里面的
private_data
得到
struct socket
,根据里面
ops
的定义,调用
inet_sendmsg
函数。Sock 层:从
struct socket
里面的
sk
得到
struct sock
,根据里面
sk_prot
的定义,调用
tcp_sendmsg
函数。TCP 层:
tcp_sendmsg
函数会调用
tcp_write_xmit
函数,
tcp_write_xmit
函数会调用
tcp_transmit_skb
,在这里实现了 TCP 层面向连接的逻辑;完成TCP头添加传递给IP层。IP 层:扩展
struct sock
,得到
struct inet_connection_sock
,根据里面
icsk_af_ops
的定义,调用
ip_queue_xmit
函数。IP 层:
ip_route_output_ports
函数里面会调用
fib_lookup
查找路由表。FIB 全称是 Forwarding Information Base,转发信息表,也就是路由表。填写 IP 层的头。还要做的一件事情就是通过
iptables
规则。完成IP头添加后,IP 层接着调用
ip_finish_output
进行 MAC 层处理。MAC 层需要 ARP 获得 MAC 地址,因而要调用
___neigh_lookup_noref
查找属于同一个网段的邻居,它会调用
neigh_probe
发送 ARP。有了 MAC 地址,添加MAC头后,就可以调用
dev_queue_xmit
发送二层网络包了,它会调用
__dev_xmit_skb
会将请求放入队列,最后到达设备层。设备层:网络包的发送会触发一个软中断
NET_TX_SOFTIRQ
来处理队列中的数据。在软中断处理函数中,会将网络包从队列上拿下来,调用网络设备的传输函数
ndo_xmit_frame
,将网络包发到设备的队列上去。
到此上层应用发送的网络数据包已到达EOE虚拟网络设备驱动中,如何将上层应用的网络数据报通过EtherCAT EOE 发送给从站,这需要主站来实现,具体实现机制后面详细分析。接收从站应用网络数据包是一个相反的过程。
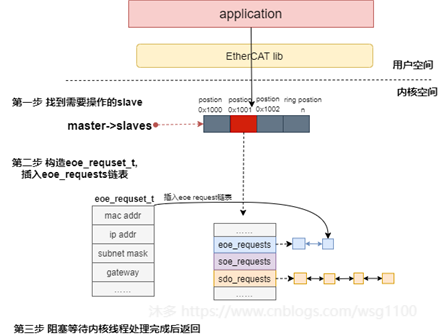
2.2 EoE request实现
对于
Set IP Parameter request
、
Set MAC Filter request
类似IgH
SDO upload/download
请求机制,简述如下。
- 通过
ioctl()
向应用提供
Set IP Parameter
、
Set MAC Filter
请求的接口。 - 各参数通过
ioctl
传递到内核后,根据参数找到需要操作的从站对象,构建eoe request对象
eoe_request_t
,插入到从站对象
eoe_requests
链表中,然后阻塞等待内核线程执行状态机处理完成。
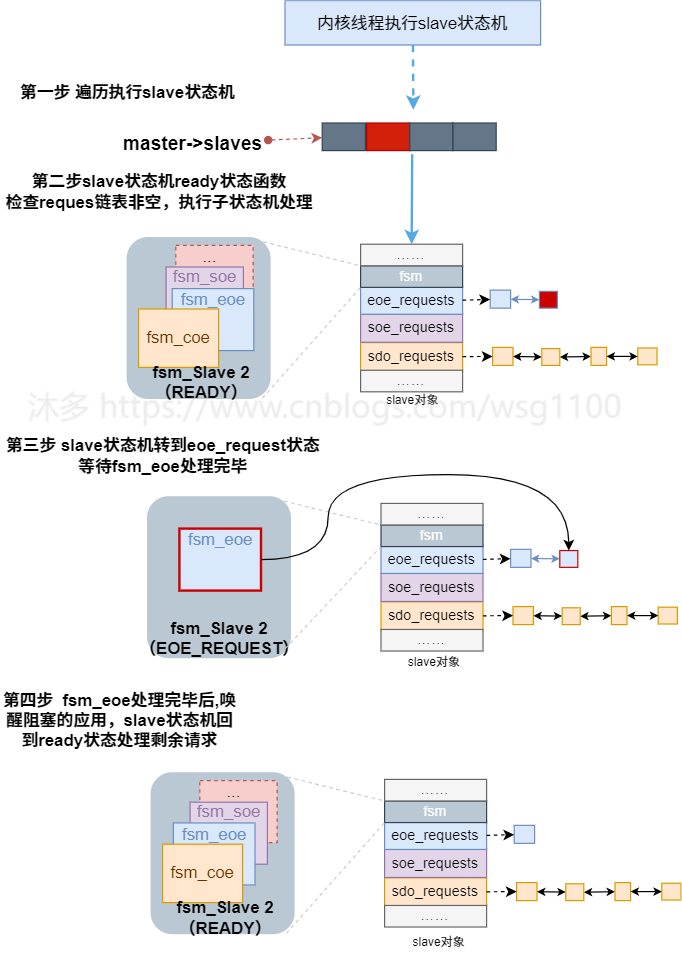
状态机方面,类似slave状态机下处理sdo下载请求的子状态机
fsm_coe
,在slave状态机下新添加处理eoe请求的子状态机
fsm_eoe
。内核线程执行slave状态机过程中,slave状态机的READY状态函数判断从站对象的
eoe_requests
链表是否有挂起的请求需要处理(链表非空),有则初始化并执行子状态机
fsm_eoe
来处理链表上的request。fsm_eoe
状态机执行,与从站邮箱通信完成
Set IP Parameter
后,唤醒阻塞的用户态应用。内核线程继续执行slave状态机的下一个状态。
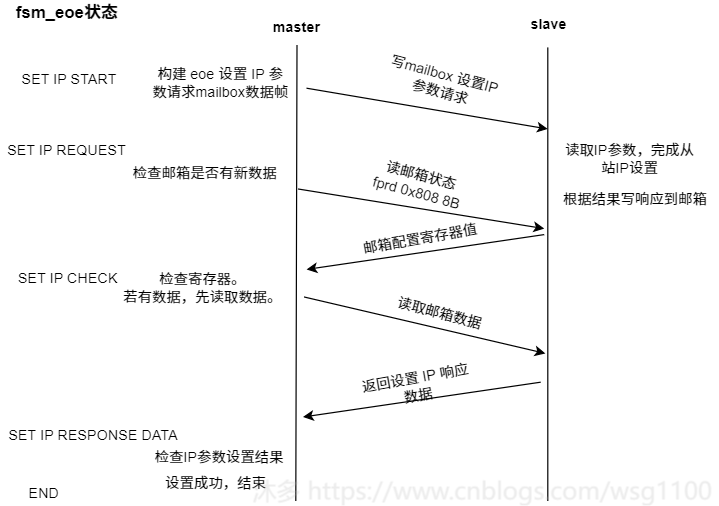
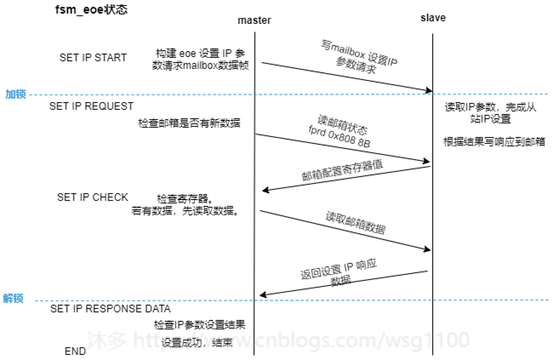
Fsm_eoe状态机状态状态转换如下:
SET_IP_START
:
设置Ip参数入口,检查邮箱EOE支持情况,构造设置 ip 请求箱帧,
发送数据帧,SET_IP_REQUEST状态。SET_IP_REQUEST
: 设置IP参数请求帧已接收
,
发送查询邮箱数据帧,检查邮箱是否有数据,转到SET_IP_CHECK状态。SET_IP_CHECK
:查询邮箱数据帧已接收,如果从站邮箱有数据,则发送取邮箱数据帧,转到SET_IP_RESPONSE状态。SET_IP_RESPONSE
:
邮箱数据帧已接收
,若邮箱数据是set IP request 响应数据,检查结果,转到结束或出错。
若不是响应数据,则继续发送查询邮箱数据帧,跳转到SET_IP_CHECK继续检查。
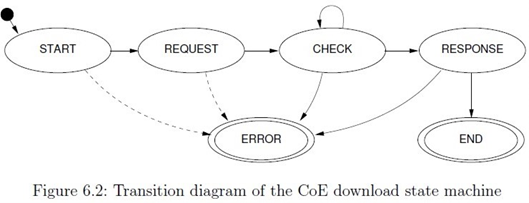
Fsm_eoe状态转换、与从站邮箱数据交互如图所示:
2.3 EoE Frament实现
5.2中,linux网络应用数据经过协议栈层层封装,调用网络设备的传输函数
ndo_xmit_frame
,将网络包发到EOE虚拟网络设备后,主站需要一种机制将EOE虚拟网络设备中的网络数据包通过EtherCAT数据帧发送到从站。
同时,主站需要查询邮箱,将从站TCP/IP应用需要发送的标准以太网数据通过邮箱协议读取,解析并提交给linux网络协议栈接收处理。
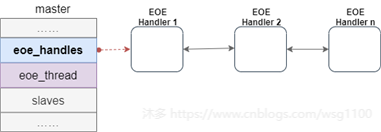
2.3.1.EoE Handler
虚拟EoE接口、EOE帧请求状态机和相关功能封装在
ec_eoe_t
类中,称为EoE handler。每个EOE虚拟网卡对应一个EoE handler。主站扫描从站过程中,根据从站对邮箱协议支持情况,为EoE从站创建虚拟设备,同时创建EOE handler,并将EOE handler放到EoE虚拟设备的私有数据中。
主站使用链表
eoe_handlers
来管理主站下的EoE handler,创建后的EoE handler插入该链表中,方便后续内核线程遍历处理。
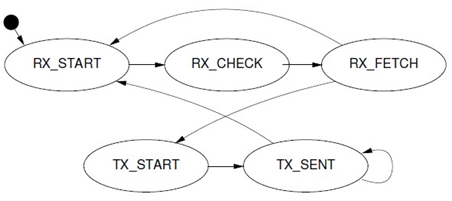
2.3.2 EoE 状态机
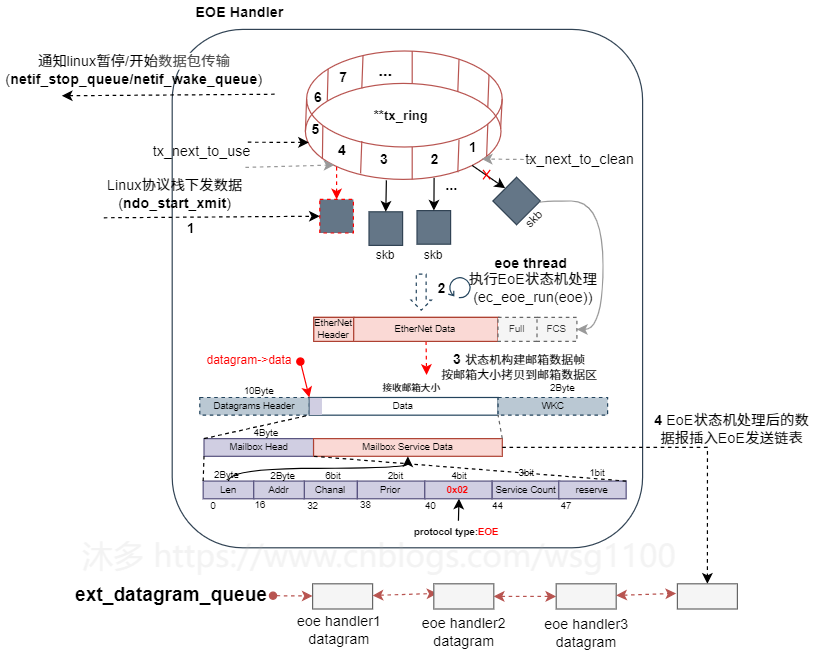
每个EOE数据(以太网数据包)通过邮箱分段发送和接收,根据邮箱的交互特性,则每个EOE handler需要一个状态机来完成EOE数据收发工作。
RX_START
:EOE状态机起始状态,
发送邮箱查询数据帧
查询从站邮箱是否新数据。发送后跳转
RX_CHECK
状态。RX_CHECK
:
邮箱查询数据帧已接收
,若从站邮箱没有数据,转到
TX_START
开始写邮箱数据。
若邮箱有新数据,
发送读取邮箱数据帧
读取邮箱数据,转到
RX_FETCH
。
- RX_FETCH
:
读取邮箱数据帧已接收,
如果邮箱数据不是“EoE Fragment request”,结束读流程转到发送流程TX_START。
如果接受的邮箱数据是一个”EOE Fragment request”如果是一个起始帧,则分配一个新的socket_buffer,否则填充到已有的socket_buffer的正确的位置,转到
RX_START
继续接收。
如果是最后一个帧,将socket_buffer提交到linux网络协议栈处理,完成一个接收流程,开始发送流程,转到
TX_START
状态。
- TX_START
:开始一个发送序列,检查
tx_ring
是否有网络数据包需要发送,如果没有,转到
RX_START
开始一个新的接收序列。
检查一个skb是否发送完毕,若完全发送成功,将其从
tx_ring
删除,通知linux可以继续往网络设备下发数据包。开始发送一个新的skb的第一个EOE帧,转到
TX_SENT
.
- TX_SENT:
根据WKC检查第一个EOE帧是否发送成功,第一个EOE帧发送成则转到
TX_SENT
发送下一个帧
,
直到整个skb发送完。
如果skb的最后一帧发送成功,转到RX_START 开始一个新的接收序列。
2.3.3 EoE 线程
每个EOE虚拟网卡对应一个EoE handler,多个从站就需要多个handler,且Linux协议层下发的skb远大于邮箱大小,每个skb需要多次邮箱通信才能完成一个skb发送,若将所有handler放到
idle_thead
或
operat_thead
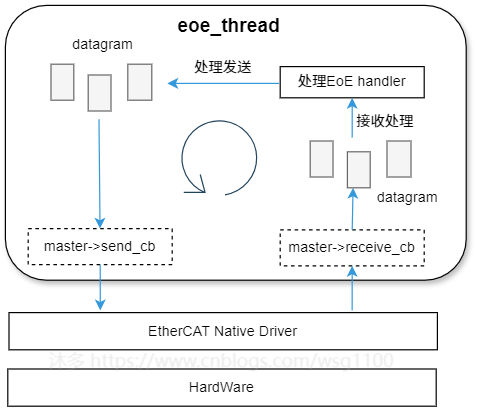
去处理,不仅严重影响其他数据交互的及时性,而且每几个周期只能发送或接收一个EoE片段,这导致数据速率非常低,因为在应用程序周期之间的时间内未执行EoE状态机,EoE数据速率将取决于应用程序任务的周期。
为解决这些问题,故在主站中单独使用一个内核线程
eoe_thead
来处理所有
EoE handler
,在从站邮箱空闲时进行EOE数据发送,保证了带宽的恒定。
添加eoe线程后带来一些其他问题,如从站邮箱并发操作、xenomai实时应用与eoe并发访问主站发送等,需要一定机制解决,这在后面章节4.5介绍。
EOE线程每周期处理一个状态,所以EOE线程的运行周期决定EOE通讯延迟,即与操作系统调度强相关。
2.3.4 TX Ring
为提高各EOE数据吞吐量,充分利用EtherCAT剩余带宽,为每个虚拟网络设备添加
skb_buff
发送缓冲区队列
tx_ring
。每次内核通过接口的
hard_start_xmit()
回调进行发送一个skb时,将这个skb插入
tx_ring
中,再由
eoe_thead
执行EoE handler处理发送;EoE Handler 处理过程中根据
tx_ring
的容量情况通知linux协议栈暂停/开始向该EoE虚拟设备发送数据,以控制流量。
对于接收,EtherCAT总线带宽100Mbps,考虑到是多个从站共同使用、且带宽不完全由EoE占用,上层linux能及时处理,暂不需要。
2.3.5 EoE 处理流程简述
- 协议栈处理后的网络数据包skb,通过EOE虚拟设备驱动提供的回调函数
ndo_xmit_frame()
插入EoE handler的
tx_ring
中,如果该队列已满,则通过调用
netif_stop_queue()
来通知上层暂停新skb的下发。
- EoE线程循环处理主站下处于激活状态的
EoE Handler
,即执行状态机EoE状态机,解析或填充datagram。
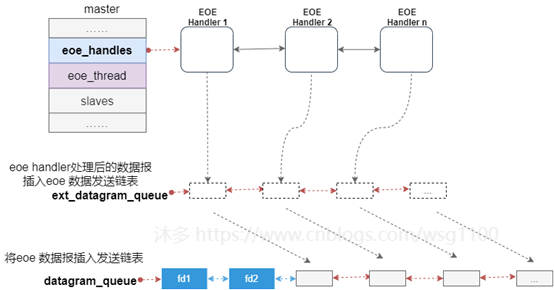
执行完所有的
EoE handler
一个状态后,状态机已构建好EoE通信数据报,调用eoe发送回调函数,将这些数据报对象,插入eoe发送链表
ext_datagram_queue
.先将
ext_datagram_queue
上的数据报转移到主发送链表
datagram_queue
,再调用主发送函数
ecrt_master_send()
发送,发送过程与2.4节数据报发送流程一致。
2.4. 共享资源访问控制
若Ether CAT主站仅使用邮箱的CoE功能,CoE功能相关状态机由内核线程
idle_thead
(或
operat_thead
)执行。在此基础上实现EOE功能需要添加内核线程eoe_thread来处理EoE数据,因为两个线程都需要访问主站总线、从站邮箱,所以总线和从站邮箱会成为两个内核线程的共享资源,对它们的访问必须按顺序进行。
2.4.1 主站
多任务下,主站总线是共享资源,必须按顺序对它进行访问。
IDLE阶段
主站IDLE阶段,内核EoE线程、
idle_thead
都需要调用主站发送函数
ecrt_master_send()
访问总线,这个阶段总线顺序访问由master对象中的信号量
io_sem
来保证。
Operation阶段
应用请求主站后,主站处于operation状态,此时
idle_thead
退出,所以总线便成为
EoE线程
与
周期应用程序
之间的共享资源,这时需要根据具体的操作系统来解决。
对于普通linux应用,使用普通内核信号量即可,
在
ioctl
系统调用发送的操作前后使用io_sem来保证
。对于Xeomai和RTAI应用,需要区分内核态和用户态:
- 对于
用户态应用
,若用按普通linux的方式,使用普通内核信号量,会导致实时任务切换到非实时域,影响周期任务实时性。正确的解决方式为有两种:
方法一、将内核线创建为xenomai内核线程,且使用xenomai内核锁来避免域切换(整个协议栈使用xenomai实现,工作量较大)
。
方法二、将EOE处理循环通过ioctl导出到用户空间,由xenomai用户线程来驱动EOE的处理。
- 对于
内核态应用
,使用IgH已有的方式,
内核应用必须负责提供适当的锁定机制和回调函数
,如果另一个实例想要访问主站,则它必须通过回调请求总线访问,如下图所示。
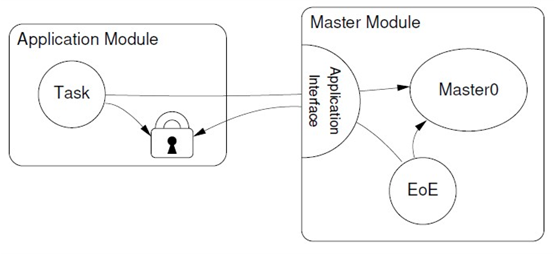
风险:周期应用与EOE线程对主站总线的顺序访问,可能加大周期数据的抖动。
2.4.2 slave邮箱
对于邮箱,若不按顺访问,可能出现如下情况
假如主站先后成功对同一个从站下发COE和EoE请求,但从站先将COE响应还是EoE响应写到邮箱未知,若此时邮箱内为EoE响应数据可读,由于读取报文前后的不确定性,可能造成CoE 状态机读取了EoE响应数据,CoE状态机处理时检测到数据类型错误而丢弃。而EoE读取失败,两个状态机均无法正常执行。
为此解决办法是
只让一个状态机去取邮箱数据
,slave对象中添加一个标志表示邮箱有没有被使用,使用mutex或原子变量来保护该变量,当状态机要读邮箱时先判断该标识,若邮箱已被其他状态机使用,先跳转到下一个状态或重试。
这只能保证只有一个线程中的状态机取数据,但还没解决邮箱数据与执行读的状态机不一致导致数据丢失的问题,所以还要解决数据丢失问题:
a. 抽象邮箱数据为ec_mbox_data_t,为每个从站状态机添加从站支持的协议对应的邮箱数据对象ec_mbox_data_t,如下。

b. 主
站接收到
EtherCAT
数据帧解析子报文时,加入报文解析步骤
,解析报文,看是否符合邮箱数据格式,若符合根据邮箱数据类型分别拷贝到对应的ec_mbox_data_t对象中,如接收的报文满足COE邮箱数结构,则将报文数据保存到mbox_coe_data中。这样不论该数据是哪个状态机读取的,该数据都会得到保存。
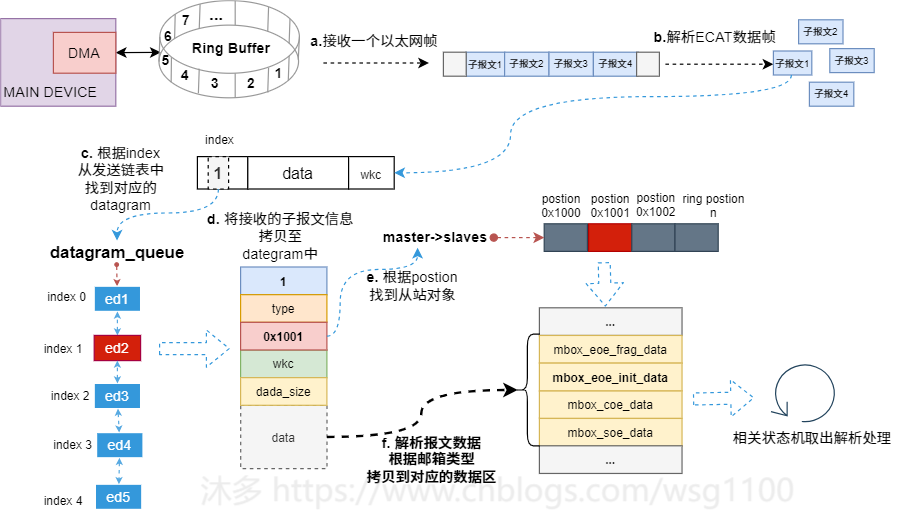
c. 修改邮箱相关状态机,状态机读邮箱数据时,若邮箱已被占用,直接跳转下一个状态,先检查对应的
ec_mbox_data_t
有无数据,有则处理,没有则回到上check状态重试。
风险:每个子报文数据都需要判断是否为邮箱数据,并解析,增加CPU资源、一周期内主站时间消耗增加;
接收过程中,目前从站对象、数据报之间的查找关系通过遍历链表来实现,随着从站数据量增加,时间复杂度呈线性增长,是否考虑通过其他数据结构优化。
3. EOE虚拟网络设备管理
3.1 Linux Bridge介绍
主站为每个EOE从站创建了虚拟网络设备,有了虚拟网卡,我们很自然就会联想到让网卡接入到交换机里,来实现多个容器间的相互连接。而Linux Bridge就是 Linux 系统下的虚拟化交换机,虽然它是以“网桥”(Bridge)而不是“交换机”(Switch)为名,但在使用过程中,你会发现 Linux Bridge 看起来像交换机,功能使用起来像交换机、程序实现起来也像交换机,所以它实际就是一台虚拟交换机。
Linux Bridge 是在 Linux Kernel 2.2 版本开始提供的二层转发工具,由brctl命令创建和管理。Linux Bridge 创建以后,就能够接入任何位于二层的网络设备,无论是真实的物理设备(比如 eth0),还是虚拟的设备(比如 veth 或者 tap),都能与 Linux Bridge 配合工作。当有二层数据包(以太帧)从网卡进入 Linux Bridge,它就会根据数据包的类型和目标 MAC 地址,按照如下规则转发处理:
- 如果数据包是广播帧,转发给所有接入网桥的设备。如果数据包是单播帧,且 MAC 地址在地址转发表中不存在,则洪泛(Flooding)给所有接入网桥的设备,并把响应设备的接口与 MAC 地址学习(MAC Learning)到自己的 MAC 地址转发表中。
- 如果数据包是单播帧,且 MAC 地址在地址转发表中已存在,则直接转发到地址表中指定的设备。
如果数据包是此前转发过的,又重新发回到此 Bridge,说明冗余链路产生了环路。由于以太帧不像 IP 报文那样有 TTL 来约束,所以一旦出现环路,如果没有额外措施来处理的话,就会永不停歇地转发下去。那么对于这种数据包,就需要交换机实现生成树协议(Spanning Tree Protocol,STP)来交换拓扑信息,生成唯一拓扑链路以切断环路。
刚刚提到的这些名词,比如二层转发、泛洪、STP、MAC 学习、地址转发表,等等,都是物理交换机中已经非常成熟的概念了,它们在 Linux Bridge 中都有对应的实现,所以我才说,Linux Bridge 不仅用起来像交换机,实现起来也像交换机。
不过,它与普通的物理交换机也还是有一点差别的,普通交换机只会单纯地做二层转发,
Linux Bridge 却还支持把发给它自身的数据包,接入到主机的三层协议栈中
。
对于通过brctl命令显式接入网桥的设备,Linux Bridge 与物理交换机的转发行为是完全一致的,它也不允许给接入的设备设置 IP 地址,因为网桥是根据 MAC 地址做二层转发的,就算设置了三层的 IP 地址也没有意义。然而,Linux Bridge 与普通交换机的区别是,除了显式接入的设备外,它自己也无可分割地连接着一台有着完整网络协议栈的 Linux 主机,因为 Linux Bridge 本身肯定是在某台 Linux 主机上创建的,我们可以看作是 Linux Bridge 有一个与自己名字相同的隐藏端口,隐式地连接了创建它的那台 Linux 主机。
因此,Linux Bridge 允许给自己设置 IP 地址,这样就比普通交换机多出了一种特殊的转发情况:如果数据包的目的 MAC 地址为网桥本身,并且网桥设置了 IP 地址的话,那该数据包就会被认为是收到发往创建网桥那台主机的数据包,这个数据包将不会转发到任何设备,而是直接交给上层(三层)协议栈去处理。这时,网桥就取代了物理网卡 eth0 设备来对接协议栈,进行三层协议的处理。
主站为每个EOE从站创建了虚拟网络设备,这些虚拟网络设备需要连接外网,否则上位机或其他网络设备无法与其连接,在linux下,其连接外网有
桥接
和
NAT
两种方式,两种方式如下图所示。
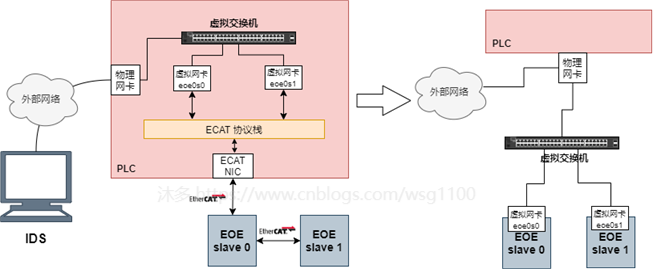
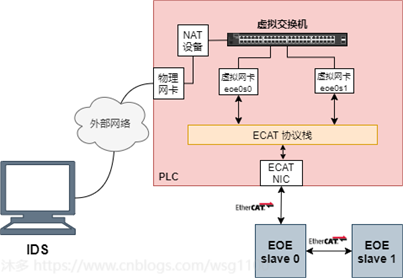
Linux中使用虚拟网桥实现图中虚拟交换机的功能,创建网桥
eoebr0
,eoe虚拟网卡都连到
eoebr0
上,与上图中不同的是,
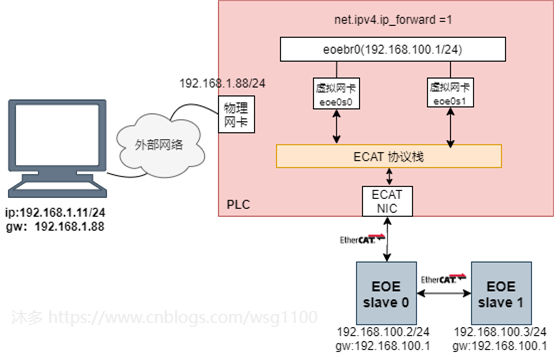
物理网卡不连接到eoebr0,通过设置 net.ipv4.ip_forward = 1,开启物理机的转发功能,同时为网桥设置ip地址,作为所有EOE虚拟网卡的网关。
这样其中物理网卡eth0收到数据包,根据数据包的目的ip地址将数据包发往网桥
eoebr0
,
eoebr0
再根据路由表继续发送数据包到EOE虚拟网卡,最后有EtherCAT master 通过EOE完成数据包到从站的传输。从站发送的EOE数据包一个相反的过程。
注: Linux内核需启用相关模块,以便支持桥接、路由。
3.2 桥接
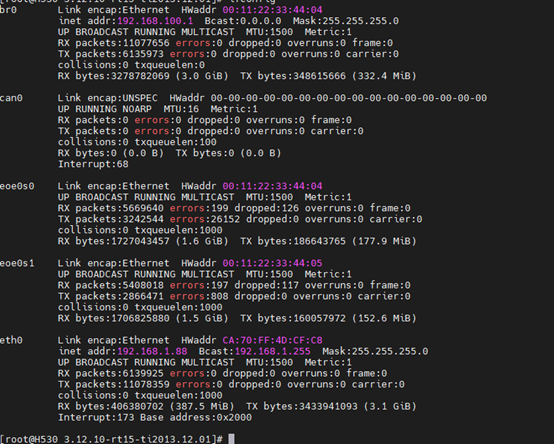
综上,创建一个包含所有EoE接口的网桥,网桥内从站EOE处于同一网段:
- 创建网桥设备
br0
$sudo brctl addbr br0
- 配置网桥设备
br0
IP
$sudo ip addr add 192.168.100.1/24 dev br0
或
$sudo ifconfig br0 192.168.57.1/24
- 向br0中添加网卡
$sudo brctl addif br0 eoe0s0
$sudo brctl addif br0 eoe0s1
- 设置eoe虚拟网卡IP并up
$sudo ifconfig eoe0s0 0.0.0.0 up
$sudo ifconfig eoe0s1 0.0.0.0 up
- 设置从站eoe Ip参数
$sudo ethercat ip addr 192.168.100.2/24 link 00:11:22:33:44:04 default 192.168.100.1 name xxx0 -p 0
$sudo ethercat ip addr 192.168.100.3/24 link 00:11:22:33:44:05 default 192.168.100.1 name xxx1 -p 1
- Up
br0
$sudo ip link set br0 up
- Down
br0
#ip link set br0 down
- 从
br0
中删除网卡
#brctl delif br0 eoe0s0
#brctl delif br0 eoe0s1
- 删除网桥
br0
#brctl delbr br0
上面的示例允许使用通过EoE连接到EtherCAT总线的子网
192.168.100.0/24
访问IPv4节点。
但是,示例使用配置命令临时配置,如果总线拓扑发生更改,则会重新创建EoE接口,并且必须再次将其添加到网桥。 因此,需使用Linux网络配置文件来保存配置,或使用
udev
脚本、应用监测网络热拔插等动态配置方式,以便自动添加出现的EoE设备。
3.3 路由
为每个EoE接口创建一个IP子网:
$ip addr add 192.168.200.1/24 dev eoe0s0
$ip addr add 192.168.201.1/24 dev eoe0s1
$echo 1 > /proc/sys/net/ipv4/ip_forward
如果它们能够在不同的EoE接口IP网络之间进行通信,则必须在连接到EoE从站的IP节点上正确设置默认网关。
如果必须设置从站IP地址和其他参数(而不是主站EoE接口),则可以通过命令行工具
ethercat ip
来实现。
ethercat ip addr 192.168.100.3/24 link 00:11:22:33:44:05 default 192.168.100.1 name xxxx -p 1
EOE虚拟网卡仅负责传输linux网络协议栈下发的数据包,可通过设置linux iptables来过滤不相关的数据包。
4. 总结
EtherCAT EoE协议与普通以太网EtherNet强相关,所以EtherCAT 主站EoE实现方式与具体的操作系统强相关,本文介绍了linux内核态igh的EoE实现方式。