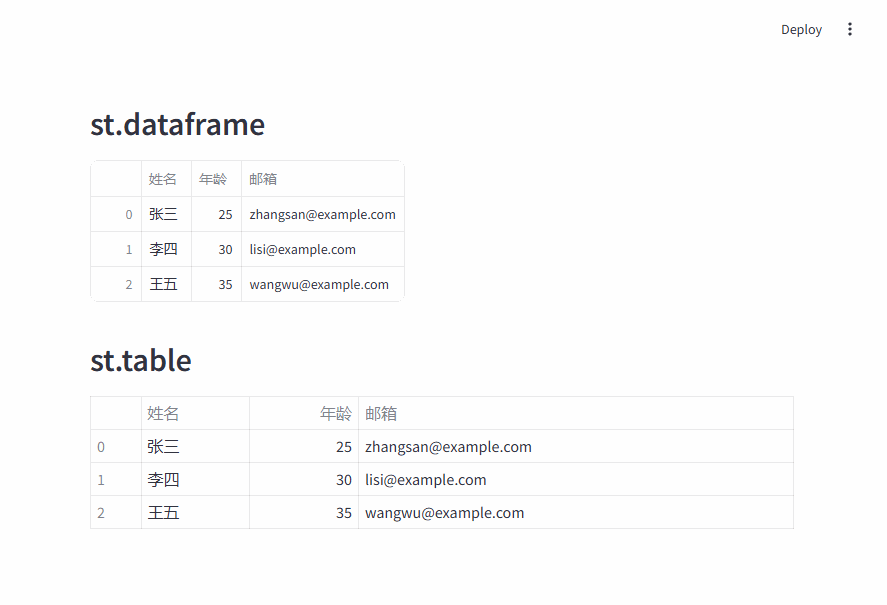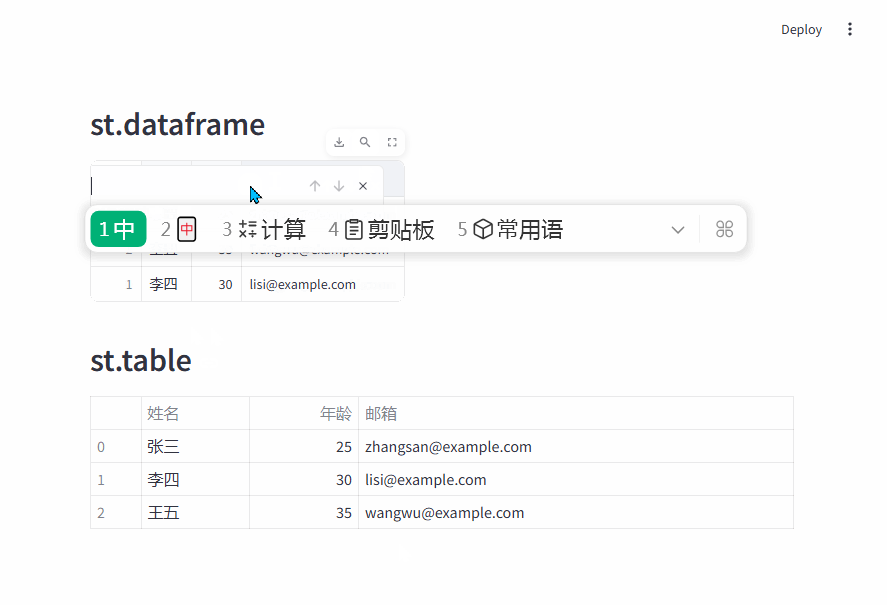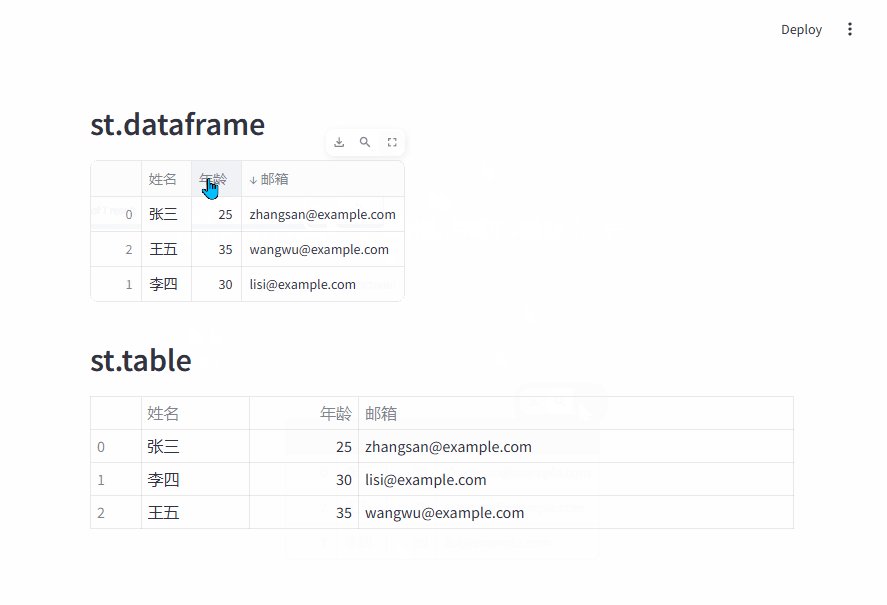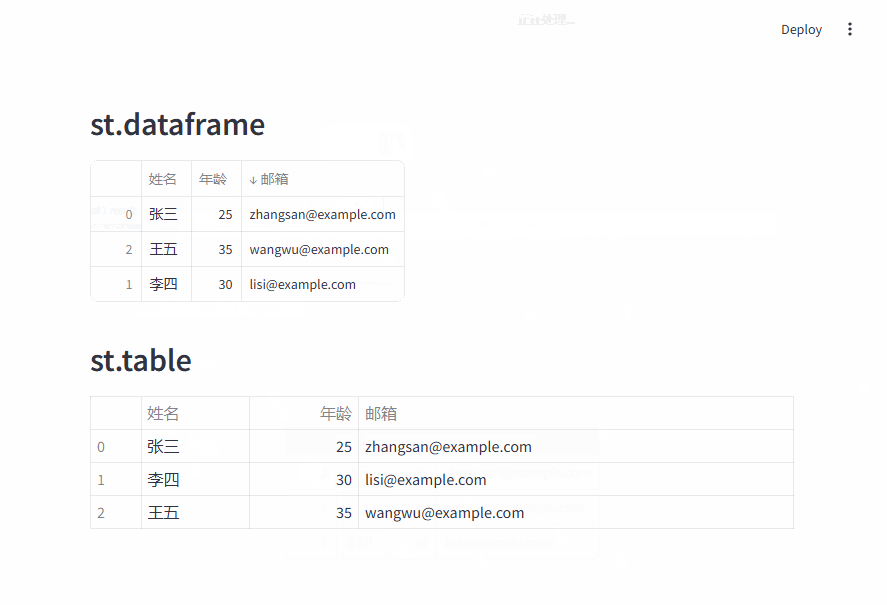
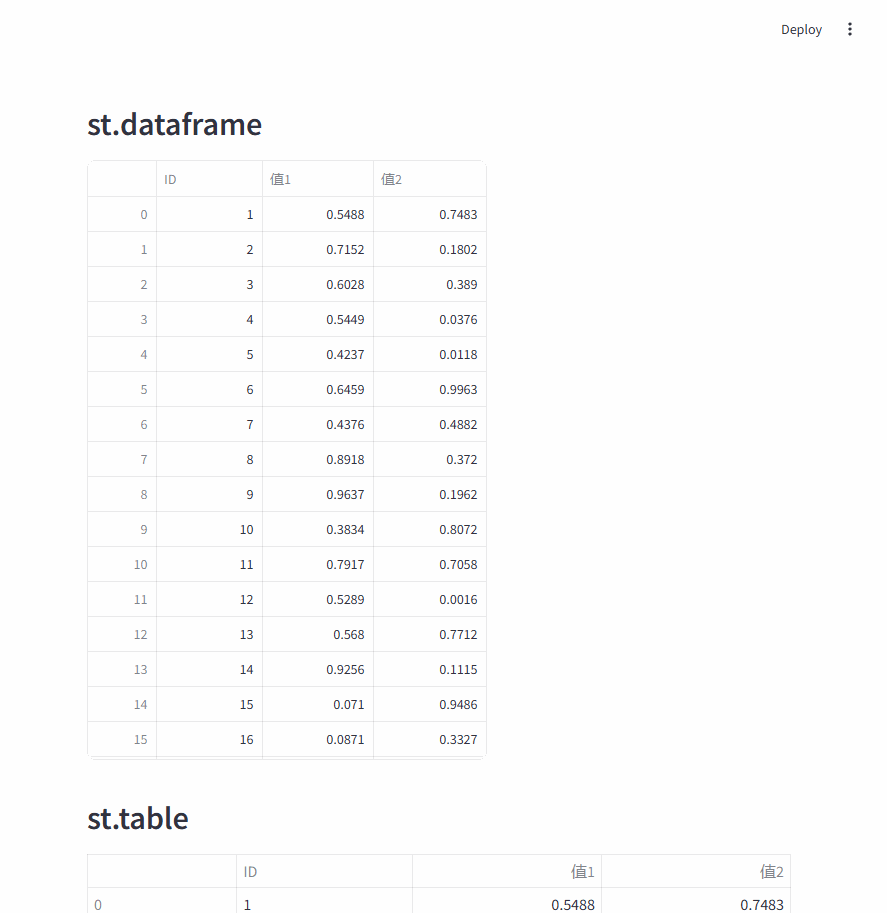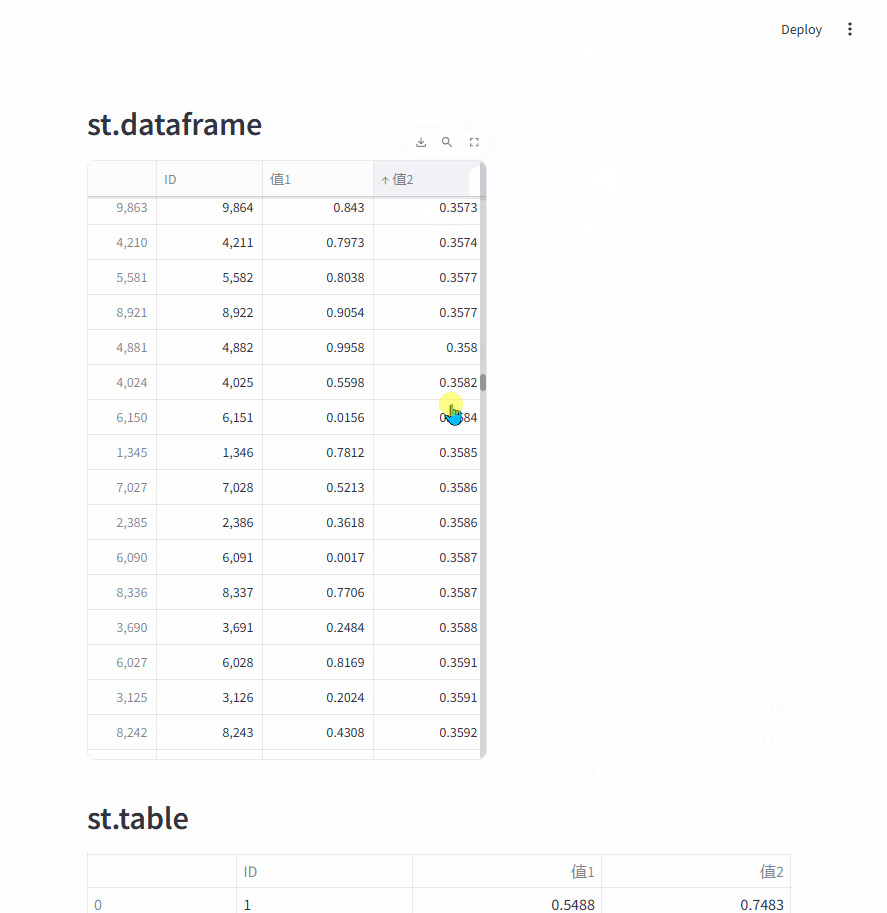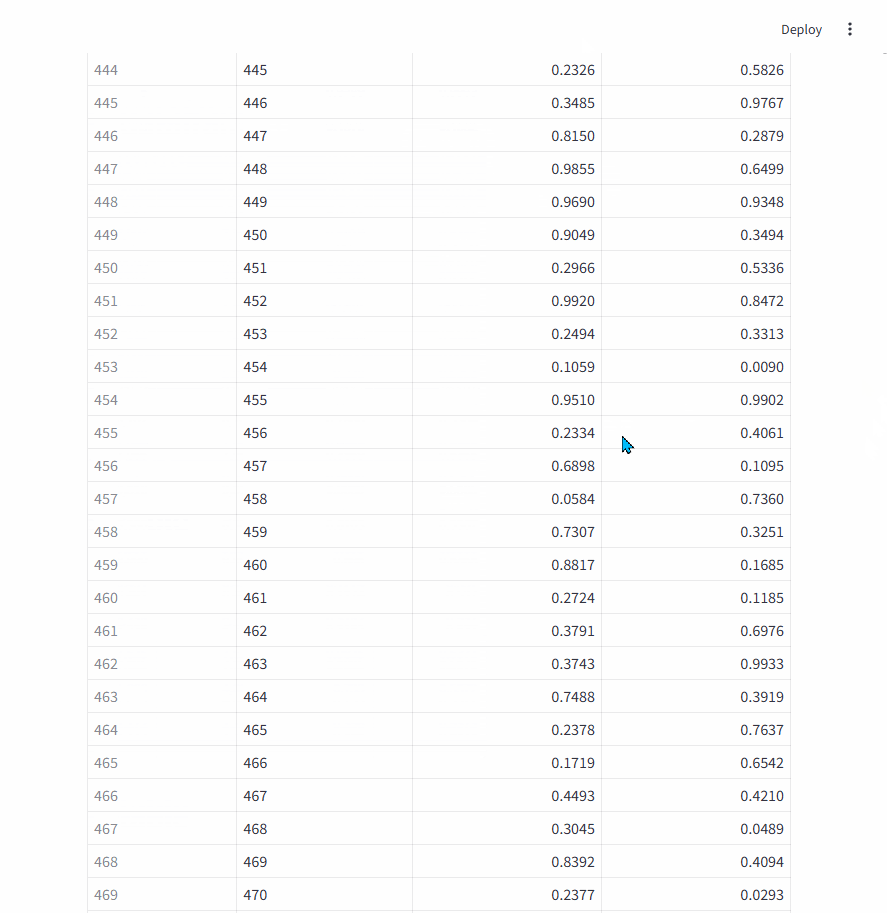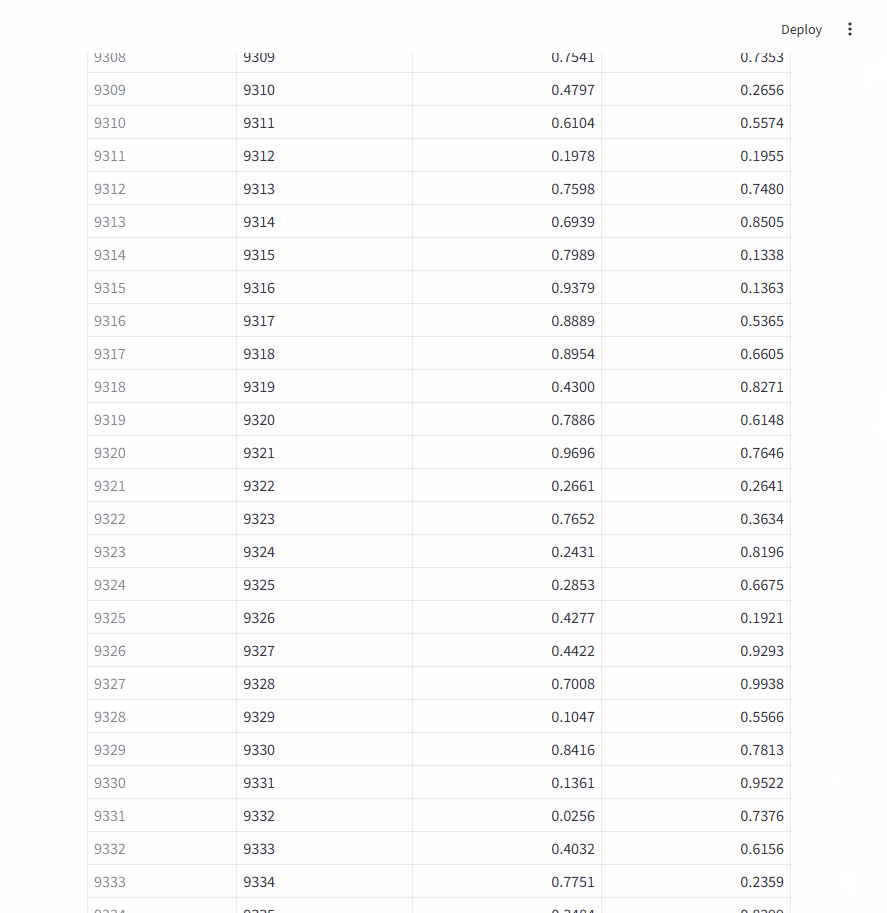
使用 C# 入门深度学习:线性代数
教程名称:使用 C# 入门深度学习
作者:痴者工良
地址:
线性代数
推荐书籍
大家都知道学习 Pytorch 或 AI 需要一定的数学基础,当然也不需要太高,只需要掌握一些基础知识和求解方法,常见需要的数学基础有线性代数、微积分、概率论等,由于高等数学课程里面同时包含了线性代数和微积分的知识,因此读者只需要学习高等数学、概率论两门课程即可。数学不用看得太深,这样太花时间了,能理解意思就行。
首先推荐以下两本书,无论是否已经忘记了初高中数学知识,对于数学基础薄弱的读者来说,都可以看。
《普林斯顿微积分读本》
《普林斯顿概率论读本》
国内的书主要是一些教材,学习难度会大一些,不过完整看完可以提升数学水平,例如同济大学出版的《高等数学》上下册、《概率论与数理统计》,不过国内的这些教材主要为了刷题解题、考研考试,可能不太适合读者,而且学习起来的时间也太长了。
接着是推荐《深度学习中的数学》,作者是涌井良幸和涌井贞美,对于入门的读者来说上手难度也大一些,不那么容易看得进去,读者可以在看完本文之后再去阅读这本经典书,相信会更加容易读懂。
另外,千万不要用微信读书这些工具看数学书,排版乱七八糟的,数学公式是各种抠图,数学符号也是用图片拼凑的,再比如公式里面中文英文符号都不分。
建议直接买实体书,容易深度思考,数学要多答题解题才行。就算买来吃灰,放在书架也可以装逼呀。买吧。
本文虽然不要求读者数学基础,但是还是需要知道一些数学符号的,例如求和∑ 、集合交并∩∪等,这些在本文中不会再赘述,读者不理解的时候需要自行搜索资料。
基础知识
标量、向量、矩阵
笔者只能给出大体的概念,至于数学上的具体定义,这里就不展开了。
标量(scalar):只有大小没有方向的数值,例如体重、身高。
向量(vector):既有大小也有方向的数值,可以用行或列来表示。
矩阵(matrix):由多行多列的向量组成。
张量(Tensor):在 Pytorch 中,torch.Tensor 类型数据结构就是张量,结构跟数组或矩阵相似。
- Tensor:是PyTorch中的基本数据类型,可以理解为多维数组。 Tensor可以用来表示数据集、模型参数和模型输出等。
- Scalar:是一个特殊类型的Tensor,只有一维。 Scalar用来表示标量值,如学习率、损失值等。
- Vector:是一个特殊类型的Tensor,有一维或两维。 Vector用来表示向量值,如梯度、特征值等。
- Matrix:是一个特殊类型的Tensor,有两维。 Matrix用来表示矩阵值,如权重矩阵、输出矩阵等。
比如说 1.0、2 这些都是标量,在各种编程语言中都以基础数据类型提供了支持,例如 C# 的基元类型。
下面将标量转换为 torch.Tensor 类型。
var x = torch.tensor(1.0);
var y = torch.tensor(2);
x.print_csharp();
y.print_csharp();
[], type = Float64, device = cpu, value = 1
[], type = Int32, device = cpu, value = 2
将数组转换为 torch.Tensor 类型:
var data = new int[ , ]{ {1, 2}, { 3, 4}};
var x_data = torch.tensor(data);
x_data.print_csharp();
由于上一章已经讲解了很多数组的创建方式,因此这里不再赘述。
Pytorch 的一些数学函数
Pytorch 通过 torch.Tensor 表示各种数据类型,torch.Tensor 提供超过 100 多种的张量操作,例如算术运算、线性代数、矩阵操作、采样等。
由于篇幅有限,这里就不单独给出,读者请自行参考以下资料:
https://pytorch.org/docs/stable/torch.html
https://pytorch.ac.cn/docs/stable/torch.html
线性代数
向量
向量的概念
在研究力学、物理学等工程应用领域中会碰到两类的量,一类完全由
数值的大小
决定,例如温度、时间、面积、体积、密度、质量等,称为
数量
或
标量
,另一类的量,
只知道数值的大小还不能完全确定所描述量
,例如加速度、速度等,这些量除了大小还有方向,称为向量。
在平面坐标轴上有两点
\(A(x_{1},y_{1})\)
、
\(B(x_{2},y_{2})\)
,以 A 为起点 、B 为终点的线段被称为被称为有向线段,其既有大小也有方向,使用 $\overrightarrow{AB} $ 表示,使用坐标表示为
\((x_{2}-x_{1},y_{2}-y_{1})\)
,如果不强调方向,也可以使用 $\alpha $ 等符号进行简记。

A、B 之间的距离称为向量的模,使用 | $\overrightarrow{AB} $ | 或 | $\overrightarrow{BA} $ | 或 | $\alpha $ | 表示。
平面中的向量,其距离公式是:
\]
其实原理也很简单,根据勾股定理,AB 的平方等于两个直角边长平方之和,所以:
\]

去平方就是:
\]
如下图所示,其两点间的距离:
\]

使用 C# 计算向量的模,结果如下
var A = torch.from_array(new[] { 1.0, 1.0 });
var B = torch.from_array(new[] { 4.0, 4.0 });
var a = B - A;
var norm = torch.norm(a);
norm.print_csharp();
[], type = Float64, device = cpu, value = 4.2426
注意,计算向量的模只能使用浮点型数据,不能使用 int、long 这些整型。
同理,对于三维空间中的两点
\(A(x_{1},y_{1},z_{1})\)
、
\(B(x_{2},y_{2},z_{2})\)
,距离公式是:
\]
向量的加减乘除法
向量的加法很简单,坐标相加即可。
如图所示,平面中有三点 A(1,1)、B(3,5)、C(6,4)。

得到三个向量分别为:$\overrightarrow{AB} (2,4)
\(、\)
\overrightarrow{BC} (3,-1)
\(、\)
\overrightarrow{AC} (5,3) $
根据数学上向量的加法可知,$\overrightarrow{AB} $ + $\overrightarrow{BC} $ = $\overrightarrow{AC} $
var B = torch.from_array(new[] { 2.0, 4.0 });
var A = torch.from_array(new[] { 3.0, -1.0 });
var a = A + B;
a.print_csharp();
[2], type = Float64, device = cpu, value = double [] {5, 3}
同理,在 Pytorch 中,向量减法也是两个 torch.Tensor 类型相减即可。
推广到三维空间,计算方法也是一样的。
var B = torch.from_array(new[] { 2.0, 3.0, 4.0 });
var A = torch.from_array(new[] { 3.0, 4.0, 5.0 });
var a = B - A;
a.print_csharp();
[3], type = Float64, device = cpu, value = double [] {-1, -1, -1}
另外,向量乘以或除以一个标量,直接运算即可,如 $ \overrightarrow{AB} (2,4) $,则 $ 3 * \overrightarrow{AB} (2,4) $ = (6,12)。
向量的投影
如图所示, $\overrightarrow{AB} (2,4) $ 是平面上的向量,如果我们要计算向量在 x、y 上的投影是很简单的,例如在 x 轴上的投影是 2,因为 A 点的 x 坐标是 1,B 点的 x 坐标是 3,所以 3 - 1 = 2 为 $\overrightarrow{AB} (2,4) $ 在 x 轴上的投影,5 - 1 = 4 是在 y 轴上的投影。

在数学上使用
\(Projx(u)\)
表示向量 u 在 x 上的投影,同理
\(Projy(u)\)
是 u 在 y 上的投影。
如果使用三角函数,我们可以这样计算向量在各个轴上的投影。
\]
\]
AC、BC 长度是 4,根据勾股定理得出 AB 长度是 $4\sqrt{2} $,由于
\(cos \frac{\pi }{2} = \frac{\sqrt{2}} {2}\)
,所以
\(Projx(u) = 4\)
。

那么在平面中,我们已知向量的坐标,求向量与 x 、y 轴的夹角,可以这样求。
\]
\]
例如上图中 $\overrightarrow{AB} (4,4) $,x 和 y 都是 4,其中
\(|v| = 4\sqrt{2}\)
,所以
\(\cos \alpha = \frac{4}{4\sqrt{2}} = \frac{\sqrt{2}}{2}\)
从 x、y 轴推广到平面中任意两个向量
\(\alpha\)
、
\(\beta\)
,求其夹角
\(\varphi\)
的公式为:
\]
继续按下图所示,计算
\(\overrightarrow{AB}\)
、
\(\overrightarrow{AC}\)
之间的夹角,很明显,我们按经验直接可以得出夹角
\(\varphi\)
是 45° 。

但是如果我们要通过投影方式计算出来,则根据 $ \frac{\alpha \cdot \beta}{|\alpha|\cdot|\beta|} $ ,是 C# 计算如下。
var AB = torch.from_array(new[] { 4.0, 4.0 });
var AC = torch.from_array(new[] { 4.0, 0.0 });
// 点积
var dot = torch.dot(AB, AC);
// 求每个向量的模
var ab = torch.norm(AB);
var ac = torch.norm(AC);
// 求出 cosφ 的值
var cos = dot / (ab * ac);
cos.print_csharp();
// 使用 torch.acos 计算夹角 (以弧度为单位)
var theta = torch.acos(cos);
// 将弧度转换为角度
var theta_degrees = torch.rad2deg(theta);
theta_degrees.print_csharp();
[], type = Float64, device = cpu, value = 0.70711
[], type = Float64, device = cpu, value = 45

柯西-施瓦茨不等式
\(a\)
、
\(b\)
是两个向量,根据前面学到的投影和夹角知识,我们可以将以下公式进行转换。
\]
\]
由于
\(-1 \le \cos \varphi \le 1\)
,所以:
\]
这个就是 柯西-施瓦茨不等式。
也就是说,当两个向量的夹角最小时,两个向量的方向相同(角度为0),此时两个向量的乘积达到最大值,角度越大,乘积越小。在深度学习中,可以将两个向量的方向表示为相似程度,例如向量数据库检索文档时,可以算法计算出向量,然后根据相似程度查找最优的文档信息。

向量的点积
点积即向量的数量积,点积、数量积、内积,都是同一个东西。
两个向量的数量积是标量,即一个数值,而向量积是不同的东西,这里只说明数量积。
数量积称为两个向量的数乘,而向量积才是两个向量的乘法。
向量的数乘公式如下:
\]
加上前面学习投影时列出的公式,如果可以知道向量的模和夹角,我们也可以这样求向量的点积:
\]
例如 $\overrightarrow{AB} (2,4)
\(、\)
\overrightarrow{BC} (3,-1) $ 两个向量,如下图所示。

计算其点积如下:
var B = torch.from_array(new[] { 2.0, 4.0 });
var A = torch.from_array(new[] { 3.0, -1.0 });
var dot = torch.dot(A, B);
dot.print_csharp();
[], type = Float64, device = cpu, value = 2
读者可以试试根据点积结果计算出
\(\angle ABC\)
的角度。
向量积
在画坐标轴时,我们默认轴上每个点间距都是 1,此时 x、y、z 上的单位向量都是 1,如果一个向量的模是 1,那么这个向量就是单位向量,所以单位向量可以有无数个。

在数学中,我们往往会有很多未知数,此时我们使用
\(i\)
、
\(j\)
、
\(k\)
分别表示与 x、y、z 轴上正向一致的三个单位向量,
在数学和物理中,单位向量通常用于表示方向而不关心其大小
。不理解这句话也没关系,忽略。
在不关心向量大小的情况下,我们使用单位向量可以这样表示两个向量:
\]
\]
在三维空间中,
\(i\)
、
\(j\)
、
\(k\)
分别表示三个轴方向的单位向量。
- \(i\)
表示沿 x 轴方向的单位向量。 - \(j\)
表示沿 y 轴方向的单位向量。 - \(k\)
表示沿 z 轴方向的单位向量。
这种方式表示 a 在 x 轴上有
\(x_{1}\)
个单位,在 y 轴上有
\(y_{1}\)
个单位,在 z 轴上有
\(z_{1}\)
个单位。
一般来说,提供这种向量表示法,我们并不关心向量的大小,我们只关心其方向,如下图所示。

现在我们来求解一个问题,在空间中找到跟 $\overrightarrow{AB}
\(、\)
\overrightarrow{BC} $ 同时垂直的向量,例如下图的 $\overrightarrow{AD} $,很明显,这样的向量不止一个,有无数个,所以我们这个时候要了解什么是法向量和单位向量。

法向量是一个与平面垂直的向量(这里不涉及曲面、曲线这些),要找出法向量也很简单,有两种方法,一种是坐标表示:
\begin{vmatrix}
&i &j &k \\
&x_{1} &y_{1} &z_{1} \\
&x_{2} &y_{2} &z_{2}
\end{vmatrix} = (y_{1}z_{2}-z_{1}y_{2})i - (x_{1}z_{2}-z_{1}x_{2})j + (x_{1}y_{2}-y_{1}x_{2})k
\]
这样记起来有些困难,我们可以这样看,容易记得。
\begin{vmatrix}
&i &j &k \\
&x_{1} &y_{1} &z_{1} \\
&x_{2} &y_{2} &z_{2}
\end{vmatrix} = (y_{1}z_{2}-z_{1}y_{2})i + (z_{1}x_{2}-x_{1}z_{2})j + (x_{1}y_{2}-y_{1}x_{2})k
\]
那么法向量
\(n\)
的
\(x = (y_{1}{z2} -z_{1}y_{2})\)
,y、z 轴同理,就不给出了,x、y、z 分别就是 i、j、k 前面的一块符号公式,所以法向量为:
\]
任何一条下式满足的向量,都跟
\(a\)
、
\(b\)
组成的平面垂直。
\]
例题如下。
求与
\(a = 3i - 2j + 4k\)
,
\(b = i + j - 2k\)
都垂直的法向量 。
首先提取
\(a\)
在每个坐标轴上的分量
\((3,-2,4)\)
,b 的分量为
\((1,1,-2)\)
。
则:
\begin{vmatrix}
&i &j &k \\
&3 &-2 &4 \\
&1 &1 &-2
\end{vmatrix} = (4-4)i + (4-(-6))j + (3-(-2))k = 10j + 5k
\]
所以法向量
\(n(0,10,5)\)
。
这就是通过向量积求得与两个向量都垂直的法向量的方法。
你甚至可以使用 C# 手撸这个算法出来:
var A = torch.tensor(new double[] { 3.0, -2, 4 });
var B = torch.tensor(new double[] { 1.0, 1.0, -2.0 });
var cross = Cross(A, B);
cross.print();
static Tensor Cross(Tensor A, Tensor B)
{
if (A.size(0) != 3 || B.size(0) != 3)
{
throw new ArgumentException("Both input tensors must be 3-dimensional.");
}
var a1 = A[0];
var a2 = A[1];
var a3 = A[2];
var b1 = B[0];
var b2 = B[1];
var b3 = B[2];
var i = a2 * b3 - a3 * b2;
var j = a3 * b1 - a1 * b3;
var k = a1 * b2 - a2 * b1;
return torch.tensor(new double[] { i.ToDouble(), -j.ToDouble(), k.ToDouble() });
}
[3], type = Float64, device = cpu 0 -10 5
由于当前笔者所用的 C# 版本的 cross 函数不对劲,不能直接使用,所以我们也可以利用内核函数直接扩展一个接口出来。
public static class MyTorch
{
[DllImport("LibTorchSharp")]
public static extern IntPtr THSLinalg_cross(IntPtr input, IntPtr other, long dim);
public static Tensor cross(Tensor input, Tensor other, long dim = -1)
{
var res = THSLinalg_cross(input.Handle, other.Handle, dim);
if (res == IntPtr.Zero) { torch.CheckForErrors(); }
return torch.Tensor.UnsafeCreateTensor(res);
}
}
var A = torch.tensor(new double[] { 3.0, -2, 4 });
var B = torch.tensor(new double[] { 1.0, 1.0, -2.0 });
var cross = MyTorch.cross(A, B);
cross.print_csharp();
[3], type = Float64, device = cpu, value = double [] {0, 10, 5}
当前笔者所用版本 other 参数是 Scalar 而不是 Tensor,这里应该是个 bug,最新 main 分支已经修复,但是还没有发布。

另外,还有一种通过夹角求得法向量的方法,如果知道两个向量的夹角,也可以求向量积,公式如下:
\]
一般来说,对于空间求解问题,我们往往是可以计算向量积的,然后通过向量积得出
\(|a| \cdot |b| \sin\alpha\)
的结果,而不是通过
\(|a| \cdot |b| \sin\alpha\)
求出
\(a \times b\)
。
关于此条公式,这里暂时不深入。
直线和平面表示法
在本小节节中,我们将学习空间中的直线和平面的一些知识。
在空间中的平面,可以使用一般式方程表达:
\]
其中 A、B、C 是法向量的坐标,即
\(n = \{A,B,C\}\)
。
首先,空间中的直线有三种表示方法,分别是对称式方程、参数式方程、截距式方程。
直线的对称式方程
给定空间中的一点
\(P_{0}(x_{0},y_{0},z_{0})\)
有一条直线 L 穿过
\(p_{0}\)
点,以及和非零向量
\(v=\{l,m,n\}\)
平行。

直线上任意一点和
\(p_{0}\)
的向量都和
\(v\)
平行,
\(\overrightarrow{P_{0}P} =\{x - x_{0},y - y_{0}, z - z_{0}\}\)
,所以其因为其对应的坐标成比例,所以其截距式方程为:
\]
直线的参数式方程
因为:
\]
所以:
\[\begin{cases}x = x_{0} + lt
\\y = y_{0} + mt
\\z = z_{0} + nt
\end{cases}
\]
这便是直线的参数式方程。
直线的一般式方程
空间中的直线可以看作是两个平面之间的交线,所以直线由两个平面的一般式方程给出:
\[\begin{cases}v_{1} = A_{1}x + B_{1}y + C_{1}z + D_{1}
\\ v_{2} = A_{2}x + B_{2}y + C_{2}z + D_{2}
\end{cases}
\]
这些公式在计算以下场景问题时很有帮助,不过本文不再赘述。
① 空间中任意一点到平面的距离。
② 直线和平面之间的夹角。
③ 平面之间的夹角。
矩阵
矩阵在在线性代数中具有很重要的地位,深度学习大量使用了矩阵的知识,所以读者需要好好掌握。
如下图所示,A 是一个矩阵,具有多行多列,
\(a_{11}、a_{12}、...、a_{1n}\)
是一个行,
\(a_{11}、a_{21}、...、a_{m1}\)
是一个列。

在 C# 中,矩阵属于二维数组,即
\(m*n\)
,例如要创建一个
\(3*3\)
的矩阵,可以这样表示:
var A = torch.tensor(new double[,]
{
{ 3.0, -2.0, 4.0 },
{ 3.0, -2.0, 4.0 },
{ 3.0, -2.0, 4.0 }
});
A.print_csharp();
使用
.T
将矩阵的行和列倒过来:
var A = torch.tensor(new double[,]
{
{ 3.0, -2.0, 4.0 }
});
A.T.print_csharp();
生成的是:
{
{3.0},
{-2.0},
{4.0}
}
如图所示:

矩阵的加减
矩阵的加减法很简单,就是相同位置的数组加减。
var A = torch.tensor(new double[,]
{
{ 1.0, 2.0, 4.0 },
{ 1.0, 2.0, 4.0 },
{ 1.0, 2.0, 4.0 }
});
var B = torch.tensor(new double[,]
{
{ 1.0, 1.0, 2.0 },
{ 1.0, 1.0, 2.0 },
{ 1.0, 1.0, 2.0 }
});
(A+B).print_csharp();
结果是:
{
{2, 3, 6},
{2, 3, 6},
{2, 3, 6}
}
如果直接将两个矩阵使用 Pytorch 相乘,则是每个位置的数值相乘,这种乘法称为 Hadamard 乘积:
var A = torch.tensor(new double[,]
{
{ 1.0, 2.0 }
});
var B = torch.tensor(new double[,]
{
{ 3.0, 4.0 }
});
// 或者 torch.mul(A, B)
(A * B).print_csharp();
[2x1], type = Float64, device = cpu, value = double [,] { {3}, {8}}
矩阵乘法
我们知道,向量内积可以写成
\(x_{2}x_{1}+y_{2}y_{1}+z_{2}z_{1}\)
,如果使用矩阵,可以写成:
&x_{1} &y_{1} &z_{1} \\
\end{bmatrix} \cdot
\begin{bmatrix}
&x_{2} \\
&y_{2} \\
&z_{2}
\end{bmatrix} = x_{2}x_{1}+y_{2}y_{1}+z_{2}z_{1}
\]
换成实际案例,则是:
&1 &2 &3\\
\end{bmatrix} \cdot
\begin{bmatrix}
&4 \\
&5 \\
&6
\end{bmatrix} = 1*4 + 2*5 + 3*6 = 32
\]
使用 C# 计算结果:
var a = torch.tensor(new int[] { 1, 2, 3 });
var b = torch.tensor(new int[,] { { 4 }, { 5 }, { 6 } });
var c = torch.matmul(a,b);
c.print_csharp();
[1], type = Int32, device = cpu, value = int [] {32}
上面的矩阵乘法方式使用 **A ⊗ B ** 表示,对于两个多行多列的矩阵乘法,则比较复杂,下面单独使用一个小节讲解。
**A ⊗ B **
矩阵的乘法比较麻烦,在前面,我们看到一个只有行的矩阵和一个只有列的矩阵相乘,结果只有一个值,但是对于多行多列的两个矩阵相乘,矩阵每个位置等于 A 矩阵行和 B 矩阵列相乘之和。
比如下面是一个简单的
2*2
矩阵。
\[\begin{bmatrix}
&a_{11} &a_{12} \\
&a_{21} &a_{22}
\end{bmatrix} \cdot
\begin{bmatrix}
&b_{11} &b_{12} \\
&b_{21} &b_{22}
\end{bmatrix}
=
\begin{bmatrix}
&c_{11} &c_{12} \\
&c_{21} &c_{22}
\end{bmatrix}
\]
因为
\(c_{11}\)
是第一行第一列,所以
\(c_{11}\)
是 A 矩阵的第一行乘以 B 第一列的内积。
\begin{bmatrix}
&a_{11} &a_{12}
\end{bmatrix} \cdot
\begin{bmatrix}
&b_{11} \\
&b_{21}
\end{bmatrix}
= a_{11}*b_{11}+a_{12}*b_{21}
\]
因为
\(c_{12}\)
是第一行第二列,所以
\(c_{12}\)
是 A 矩阵的第一行乘以 B 第二列的内积。
\begin{bmatrix}
&a_{11} &a_{12}
\end{bmatrix} \cdot
\begin{bmatrix}
&b_{12} \\
&b_{22}
\end{bmatrix}
= a_{11}*b_{12}+a_{12}*b_{22}
\]
因为
\(c_{21}\)
是第二行第一列,所以
\(c_{21}\)
是 A 矩阵的第二行乘以 B 第一列的内积。
\begin{bmatrix}
&a_{21} &a_{22}
\end{bmatrix} \cdot
\begin{bmatrix}
&b_{22} \\
&b_{21}
\end{bmatrix}
= a_{21}*b_{11}+a_{22}*b_{21}
\]
因为
\(c_{22}\)
是第二行第二列,所以
\(c_{22}\)
是 A 矩阵的第二行乘以 B 第二列的内积。
\begin{bmatrix}
&a_{21} &a_{22}
\end{bmatrix} \cdot
\begin{bmatrix}
&b_{12} \\
&b_{22}
\end{bmatrix}
= a_{21}*b_{12}+a_{22}*b_{22}
\]
例题如下:
\[\begin{bmatrix}
&1 &2 \\
&3 &4
\end{bmatrix} \cdot
\begin{bmatrix}
&5 &6 \\
&7 &8
\end{bmatrix}
=
\begin{bmatrix}
&(1*5 + 2*7) &(1*6 + 2*8) \\
&(3*5 + 4*7) &(3*6 + 4*8)
\end{bmatrix}
=
\begin{bmatrix}
&19 &22 \\
&43 &50
\end{bmatrix}
\]
使用 C# 计算多行多列的矩阵:
var A = torch.tensor(new double[,]
{
{ 1.0, 2.0 },
{ 3.0, 4.0 }
});
var B = torch.tensor(new double[,]
{
{ 5.0 , 6.0 },
{ 7.0 , 8.0 }
});
torch.matmul(A, B).print_csharp();
{ {19, 22}, {43, 50}}