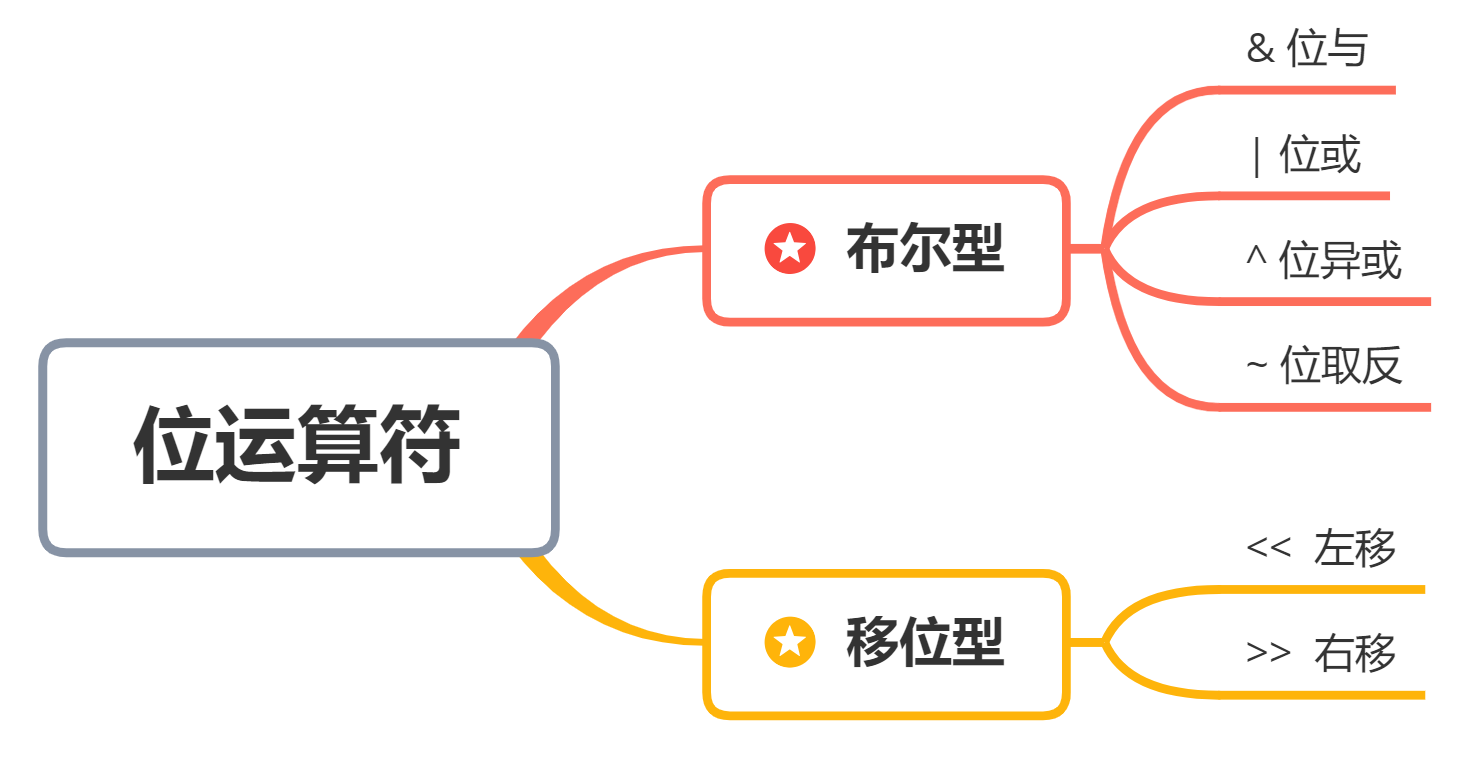
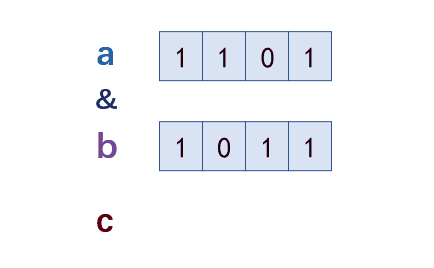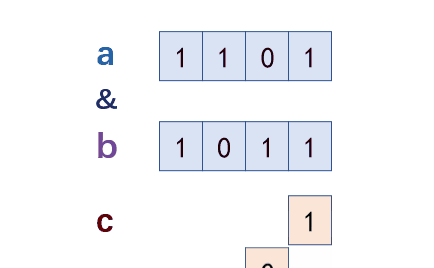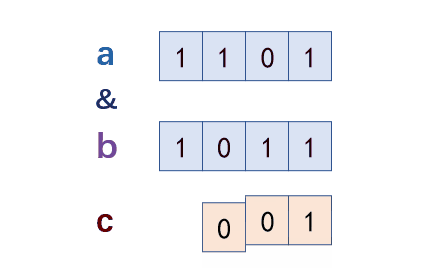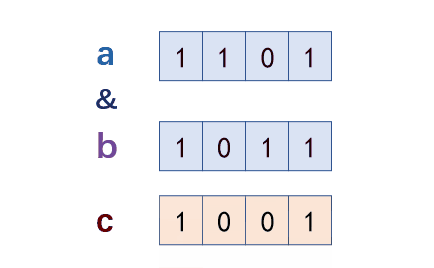
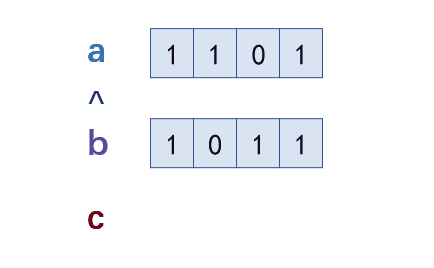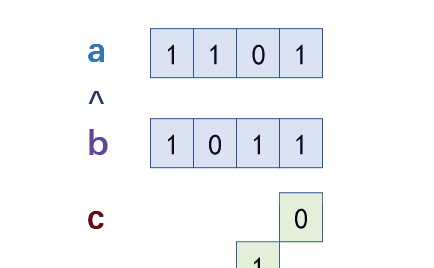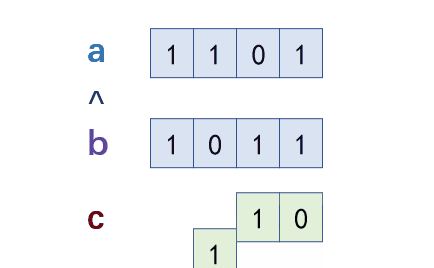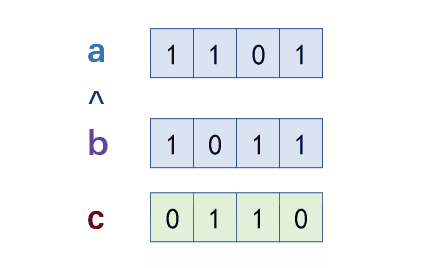
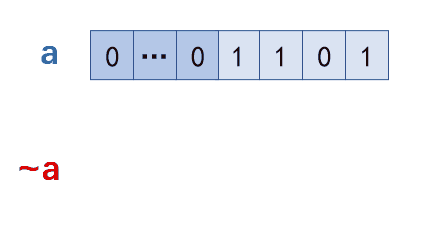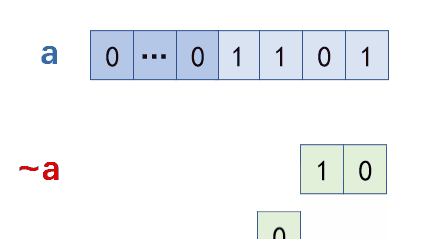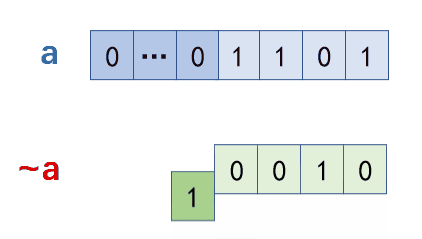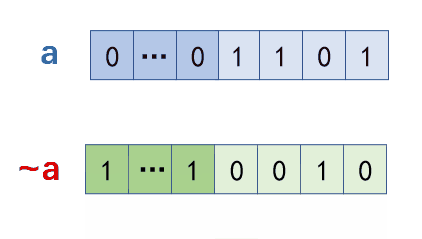
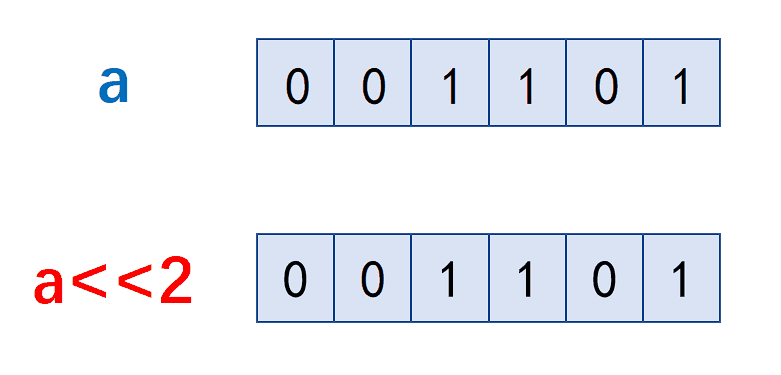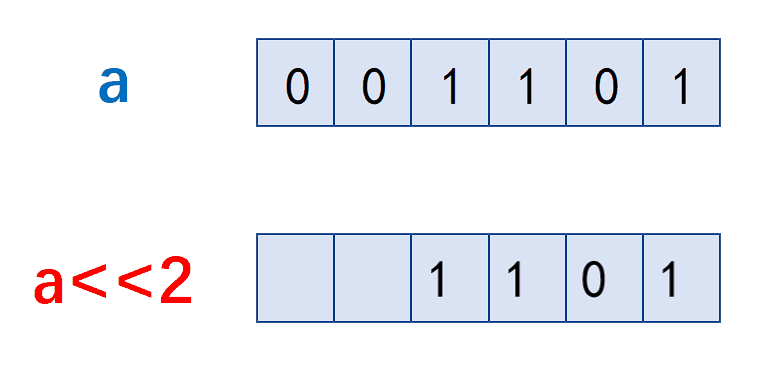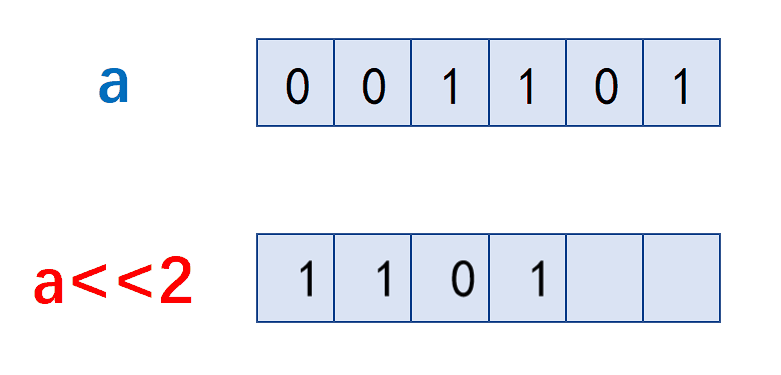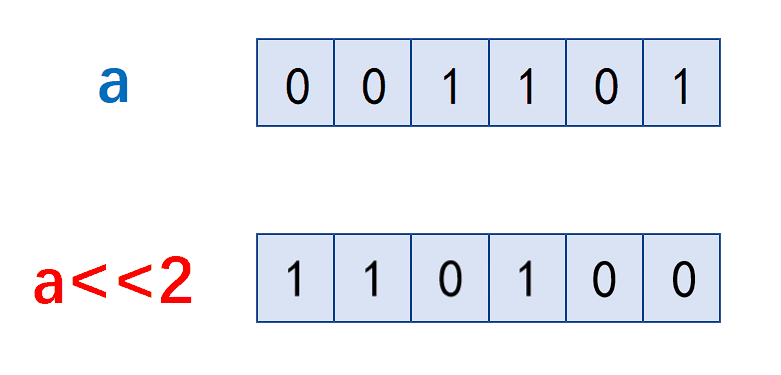
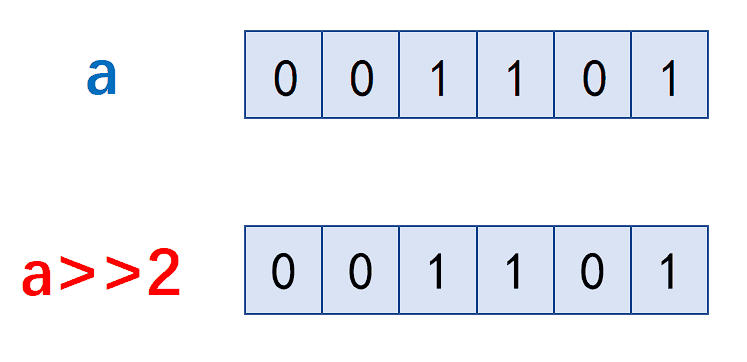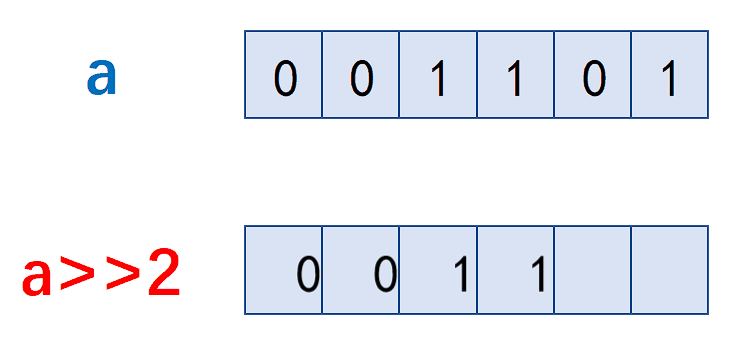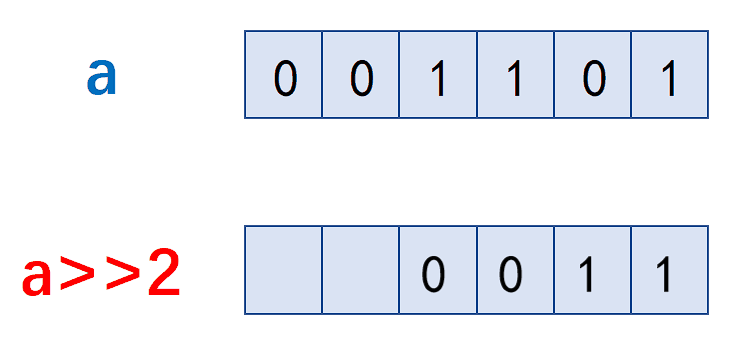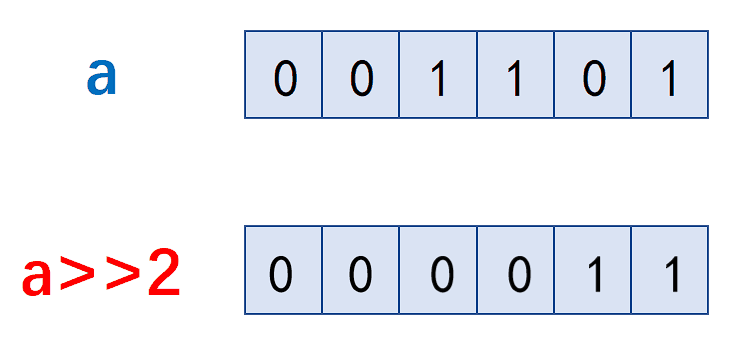
如何理解单例模式?
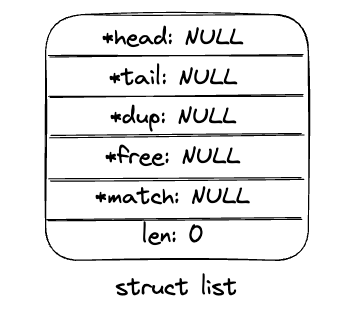
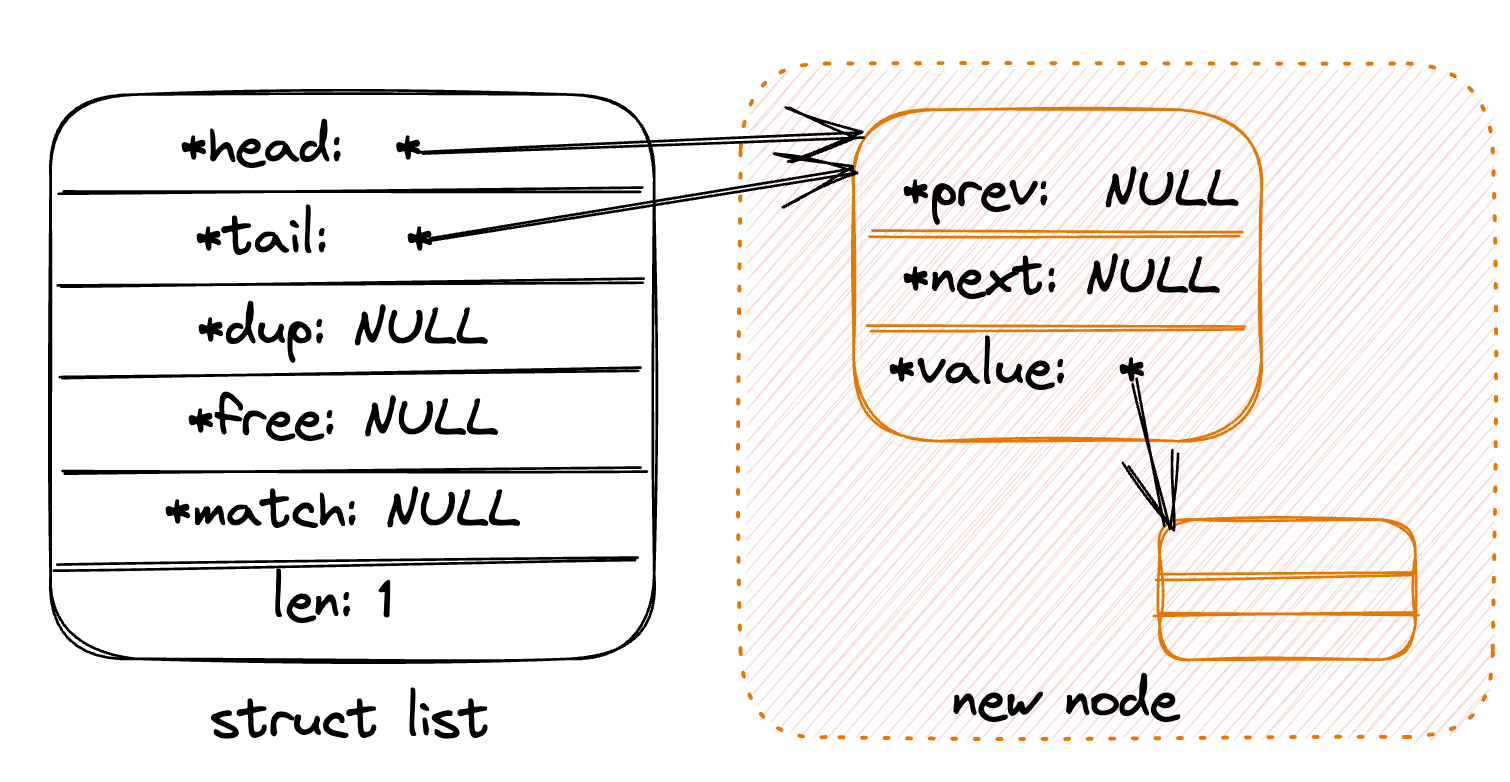
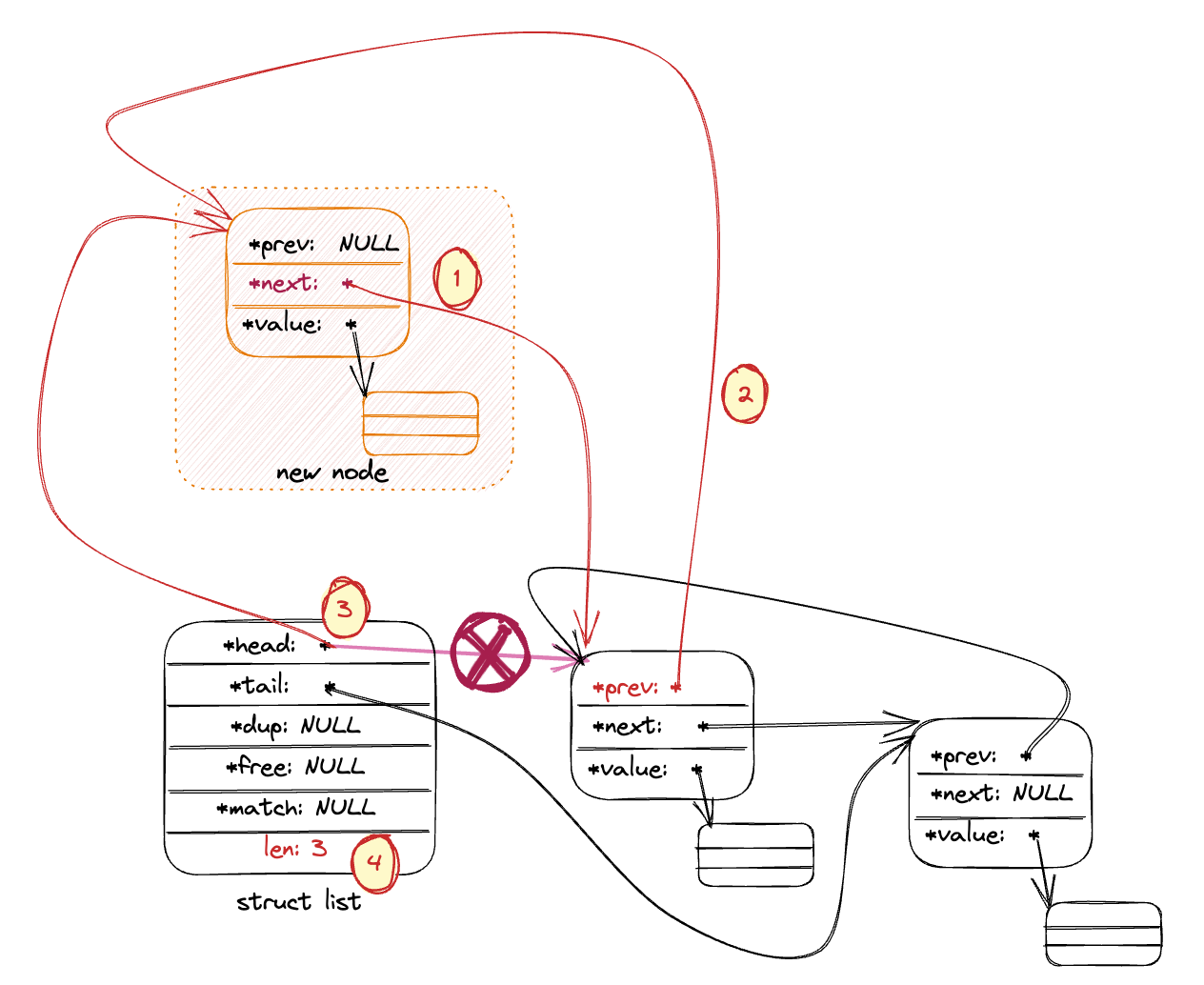
单例模式(Singleton Pattern):采取一定的方法保证在整个的软件系统中,对某个类只能存在一个对象实例,并且该类只提供一个取得其对象实例的方法。
通俗点来讲:就是一个男人只能有一个老婆,一个女人只能有一个老公
单例模式一共有8种方式实现,下面一一举例:
1、饿汉式(静态常量属性)
实现步骤
构造器私有化- 在类的内部定义
静态常量对象 - 向外暴露一个
静态的公共方法getInstance,返回一个类的对象实例
参考代码
/**
* Husband,一个女人只能有一个老公husband -> Husband实现单例模式
* 方式1:饿汉式(静态常量属性)实现单例模式
*/
public class Husband {
// 第二步:创建私有的静态常量对象
private static final Husband husband = new Husband();
// 第一步:构造器私有化
private Husband() {
}
// 第三步:向外提供一个静态的公共方法,以获取该类的对象
public static Husband getInstance() {
// 返回的永远是 同一个 husband对象
return husband;
}
}
细节说明
- 为什么构造器要私有化? -> 使外部无法创建Husband对象,只能使用已经准备好的对象 -> 不能滥情
- 为什么属性设置成final? -> 只创建这一个对象husband,以后不会再变 -> 一生只钟情一人
- 为什么设置成类变量static? -> 构造器已被私有化,外部无法创建Husband对象,需要类内部提前准备好对象 -> 在类加载时将对象准备好
- 为什么公共方法要用static? -> 非static方法属于对象,需要通过对象.方法名()调用 -> 外部类无法创建对象,在没有对象时,外部类无法访问非static方法
- 为什么叫饿汉式? -> 只要加载了类信息,对象就已经创建好 -> 只要饿了,就吃东西
优缺点
- 优点:实现了在整个软件过程中创建一次类的对象,不存在线程安全问题(反射会破坏单例模式安全性),调用效率高
- 缺点:如果只加载了类,并不需要用到该类对象,对象也已经创建好 -> 存在内存资源浪费问题。
2、饿汉式(静态代码块)
实现步骤
- 构造器私有化
- 定义静态常量不初始化
- 静态代码块中为类属性初始化创建对象
- 向外提供一个静态的公共方法,以获取该类的对象
参考代码
/**
* Husband,一个女人只能有一个老公 -> Husband实现单例模式
* 方式2:饿汉式(静态代码块)实现单例模式
*/
public class Husband {
// 第二步:创建私有的静态常量对象
private static final Husband husband;
static {
husband = new Husband();
}
// 第一步:构造器私有化 -> 外部无法创建该类对象,只能使用已经准备好的对象
private Husband() {
}
// 第三步:向外提供一个静态的公共方法,以获取该类的对象
public static Husband getInstance() {
// 返回的永远是 同一个 husband对象
return husband;
}
}
细节说明
:原理和第一种饿汉式相同,都是利用类加载时完成对象属性的创建
优缺点同上一种饿汉式
3、懒汉式(线程不安全)
实现步骤
- 构造器私有化
- 定义一个私有静态属性对象
- 提供一个公共的static方法,可以返回一个类的对象
参考代码
/**
* 一个男人只能有一个老婆wife -> Wife类实现单例模式
* 方式3:懒汉式单例模式(线程不安全)
*/
public class Wife {
// 第二步:设置私有静态属性
private static Wife wife = null;
// 第一步:构造器私有化
private Wife() {
}
// 第三步:向外提供获取对象的静态方法
public static Wife getInstance() {
if (wife == null) { // 如果没有老婆,则分配一个老婆
wife = new Wife();
}
return wife;
}
}
细节说明
- 为什么叫懒汉式? -> 即使加载了类信息,不调用getInstance()方法也不会创建对象 -> 饿了(加载类信息)也不吃东西(不创建对象),懒到一定程度。
- 为什么要if判断? -> 防止每次调用时都会重新创建新的对象 -> 防止滥情
优缺点
优点:只有需要对象时才会调用方法返回该类对象,没有则创建对象,避免了资源浪费 -> 实现了延时加载
缺点:
线程不安全
,分析if代码块:if (wife == null) { // 当线程1进入if代码块后,还没有完成对象的创建之前,线程2紧随其后也进入了if代码块内 // 此时就会出现线程1创建了对象,线程2也创建了对象 -> 破坏了单例模式 -> 线程不安全 wife = new Wife(); // 通俗的来讲:多个女生看上了同一个男生,问男生有没有老婆?男生回答没有老婆 -> 多个女生先后都当过男生的老婆 -> 前妻太多 -> 违背了单例模式的"一生只钟情一人"的核心思想 }
4、懒汉式(同步代码块)
参考代码
/**
* 一个男人只能有一个老婆wife -> Wife类实现单例模式
* 方式4:懒汉式单例模式(同步代码块,线程安全,性能差)
*/
public class Wife {
// 第二步:设置私有静态属性
private static Wife wife = null;
// 第一步:构造器私有化
private Wife() {
}
// 第三步:向外提供获取对象的静态方法
public static Wife getInstance() {
synchronized(Wife.class) { // 同步代码块,每个线程进入if判断前都需要获得互斥锁,保证同一时间只有一个线程进入
if (wife == null) {
wife = new Wife();
}
}
return wife;
}
}
说明:给if语句加上synchronized关键字,保证每一次只有一个线程获得互斥锁进入同步代码块,并且将同步代码块全部执行完之后释放锁,切换其他线程执行,类似于数据库中事务的概念(给SQL语句增加原子性),这里是给if语句增加原子性,要么全部执行,要么都不执行。
优缺点
优点:线程安全(反射会破坏安全性)
缺点:性能差 -> 只有第一次创建对象时需要同步代码,确保同一时间只有一个线程进入if语句,后面线程再调用该方法时,对象已经创建好只需要直接返回 -> 每一次线程调用该方法后,都需要等待获取其他线程释放的互斥锁 -> 浪费了大量时间在 等待获取互斥锁 上 -> 效率低下
通俗的来讲:多个女生问同一个男生有没有老婆? -> 男生回答:需要成为对象才有资格知道(设置同步代码块,线程需要获取互斥锁才能执行代码) -> 每一个女生都需要经过一段长时间的发展,处成对象(线程获取互斥锁) -> 男生告诉自己的对象自己没有老婆(一个线程进入if判断) -> 男生有了老婆(创建对象) -> 返回对象
5、懒汉式(同步方法)
参考代码
/**
* 一个男人只能有一个老婆wife -> Wife类实现单例模式
* 方式5:懒汉式单例模式(同步方法,线程安全,性能差)
*/
public class Wife {
// 第二步:设置私有静态属性
private static Wife wife = null;
// 第一步:构造器私有化
private Wife() {
}
// 第三步:向外提供获取对象的静态方法
public synchronized static Wife getInstance() { // 同步方法,原理和同步代码块实现懒汉式相同
if (wife == null) {
wife = new Wife();
}
return wife;
}
}
优缺点
:和同步代码块实现懒汉式类似,这里不过多赘述。
6、懒汉式(DCL模式⭐)
DCL模式实现懒汉式单例模式,即双重检查机制(DCL, Double Check Lock),线程安全,性能高
<- 面试重点
参考代码
/**
* 一个男人只能有一个老婆wife -> Wife类实现单例模式
* 方式6:懒汉式单例模式(DCL模式 -> 双重检查,线程安全,性能高)
*/
public class Wife {
// 第二步:设置私有静态属性
// volatile关键字:极大程度上避免JVM底层出现指令重排情况,极端情况除外
private static volatile Wife wife = null;
// 第一步:构造器私有化
private Wife() {
}
// 第三步:向外提供获取对象的静态方法
public static Wife getInstance() {
// 第一层if判断作用:当对象已经创建好时,直接跳过if语句,返回已经创建好的对象,不在等待获取互斥锁 -> 节省时间,提高性能
if (wife == null) {
// 注意:这里容易有多个线程同时进入第一层if的代码块中,等待获取对象锁
synchronized (Wife.class) { // 同步代码块,保证每个线程进入if判断前都需要获得互斥锁
// 第二层if判断作用:当有多个线程都进入了第一层if语句内,会出现线程1进入时对象为空,则创建对象,释放互斥锁,线程2获得互斥锁后如果没有第二层if判断,则直接创建对象,破坏了单例模式 -> 第二层if保证线程安全
if (wife == null) {
wife = new Wife();
// 在JVM底层创建对象时,大致分为3条指令
// 1.分配内存空间 -> 2.构造器初始化 -> 3.对象引用指向内存空间
// JVM为了执行效率,会打乱指令顺序(指令重排),有可能是1 -> 3 -> 2
// 当执行到3时,对象还没有创建完成,但是其他线程在第一层if判断已经创建好对象直接返回,显然不合理(对象属性还没有初始化完成) -> 保证指令执行顺序不被打乱(保证单条语句编译后的原子性) -> 使用volatile变量,禁止JVM优化重排指令
}
}
}
return wife;
}
}
DCL模式的两层if判断的作用:
- 第一层if:已经创建好对象时直接返回,不再排队获取互斥锁,提升效率
- 第二层if:保证线程安全
通俗的来讲:
有多个女生问同一个男生有没有老婆?
-> 男生口头回答说
没有老婆
(进入第一层if判断,如果有老婆则直接远离:不要去碰一个已婚的男人,他是一个女人的余生,不是你的男人不要情意绵绵) -> 其中一个女生和男生处成对象(一个线程获取到互斥锁) -> 经过发展后,女生和男生登记结婚,民政局办理结婚证时检查男生婚姻情况(第二层if判断) --未婚--> 成为夫妻,男生获得老婆获得老婆信息
优缺点
- 优点:性能高,线程安全,延时加载
- 缺点:由于JVM底层模型,volatile不能完全避免指令重排的情况,会偶尔出现问题,反射、序列化会破坏双检索单例。
7、懒汉式(静态内部类)
参考代码
/**
* 一个男人只能有一个老婆wife -> Wife类实现单例模式
* 方式7:懒汉式单例模式(静态内部类,线程安全,性能高)
*/
public class Husband {
private Husband() {}
private static class Wife {
private static Husband husband = new Husband();
}
public static Husband getInstance() {
return Wife.husband;
}
}
细节说明
- 静态内部类实现的单例模式同样是懒汉式 -> 外部类加载时并没有创建好对象,只有调用特定方法时才会加载静态内部类信息(内部类的静态对象属性创建完毕)
- 静态内部类的方式实现的单例模式:线程安全(只有在第一次加载内部类信息时才会创建对象),效率高(不需要获取互斥锁)
优缺点
- 优点:线程安全,效率高,实现了延迟加载
- 缺点:只适合简单的对象实例,需要创建的对象实例有复杂操作时(如要对 对象实例 进行其他赋值操作),代码会更复杂。反射会破坏单例模式。
8、饿汉式(枚举)
参考代码
enum Husband {
HUSBAND;
}
说明:除了第8种枚举类实现单例模式,其他七种模式都会被反射、序列化破坏单例模式(因为反射可以获得类的私有属性的构造器),只有枚举类实现的单例不会被反射破坏,反射无法获取到枚举类的构造方法。
优缺点
- 优点:线程安全,调用效率高,不会被反射、序列化破坏枚举单例
- 缺点:不能延时加载