论文信息

论文标题：CosFace: Large Margin Cosine Loss for Deep Face Recognition
论文作者：H. Wang, Yitong Wang, Zheng Zhou, Xing Ji, Zhifeng Li, Dihong Gong, Jin Zhou, Wei Liu
论文来源：2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition
论文地址：
download
论文代码：
download
引用次数：1594

1 介绍

当前提出的损失函数缺乏良好的鉴别能力，所以本文基于 “最大化类间方差和最小化类内方差” 的思想提出了 大边际余弦损失（LMCL）。

2 方法

2.1 引入

$\text{Softmax}$ 损失函数【指交叉熵损失函数】：

$L_{s}=\frac{1}{N} \sum_{i=1}^{N}-\log p_{i}=\frac{1}{N} \sum_{i=1}^{N}-\log \frac{e^{f_{y_{i}}}}{\sum_{j=1}^{C} e^{f_{j}}}    \quad\quad(1)$

其中，

$f_{j}=W_{j}^{T} x=\left\|W_{j}\right\|\|x\| \cos \theta_{j}$

Note
：$\theta_{j}$ 代表了 权重向量 $W_{j}$ 和 $x$ 之间的夹角；

分类任务的期望，是使得各个类别的数据均匀分布在超球面上。

NSL 损失
：【 固定权重向量 $W$ 的模长 $\|W\|=s$ 和特征向量 $x$ 的模长 $\|x\|=s$】

通过固定 $\|x\|=s$ 消除径向的变化，使得模型在角空间中学习可分离的特征。

例如，考虑二分类的情况，设 $\theta_{i}$ 表示特征向量与类 $C_{i}$（$i = 1,2$）权重向量之间的夹角。NSL 强制 $C_{1}$ 的 $\cos \left(\theta_{1}\right)>\cos \left(\theta_{2}\right)$，$C_{2}$ 也是如此，因此来自不同类的特性被正确地分类。

由于 NSL 学习到的特征没有足够的可区分性，只强调正确的分类。所以，本文在分类边界中引入余弦间隔，纳入 Softmax 的余弦公式中。

为开发一个大间隔分类器，进一步需要 $\cos \left(\theta_{1}\right)-m>\cos \left(\theta_{2}\right) $ 及 $\cos \left(\theta_{2}\right)-m>\cos \left(\theta_{1}\right)$，其中 $m \geq 0$ 是一个固定参数来控制余弦间隔的大小。由于$\cos \left(\theta_{i}\right)-m$ 低于 $\cos \left(\theta_{i}\right)$，因此对分类的约束更加严格，推广到多类：

${\large L_{l m c}=\frac{1}{N} \sum_{i}-\log \frac{e^{s\left(\cos \left(\theta_{y_{i}, i}\right)-m\right)}}{e^{s\left(\cos \left(\theta_{y_{i}, i}\right)-m\right)}+\sum_{j \neq y_{i}} e^{s \cos \left(\theta_{j, i}\right)}}} \quad\quad(4)$

其中，

$\begin{array}{l}W =\frac{W^{*}}{\left\|W^{*}\right\|}\\x =\frac{x^{*}}{\left\|x^{*}\right\|}\\\cos \left(\theta_{j}, i\right) = W_{j}^{T} x_{i}\end{array} \quad\quad(5)$

2.2 方法对比

$\text{Softmax}$ 的决策边界：
【$magin< 0$】

$\left\|W_{1}\right\| \cos \left(\theta_{1}\right)=\left\|W_{2}\right\| \cos \left(\theta_{2}\right)$

边界依赖于权重向量的大小和角度的余弦，这导致在余弦空间中存在一个重叠的决策区域。

$\text{NSL}$ 的决策边界：
【$magin= 0$】

通过去除径向变化，NSL 能够在余弦空间中完美地分类测试样本。然而，由于没有决策边际，它对噪声的鲁棒性并不大：决策边界周围的任何小的扰动都可以改变决策。

$\text{A-Softmax}$ 的决策边界：

对于 $C_{1}$，需要 $\theta_{1} \leq \frac{\theta_{2}}{m}$。然而问题是 $\text{Margin}$ 随着 $W_1$ 和 $W_2$ 之间的夹角发生变化，如果两个类的样本区分难度很大，导致 $W_1$ 和 $W_2$ 夹角很小，可能会出现 $\text{Margin}$ 很小的情况。

$\text{LMCL }$ 的决策边界：

$\begin{array}{l}C_{1}: \cos \left(\theta_{1}\right) \geq \cos \left(\theta_{2}\right)+m \\C_{2}: \cos \left(\theta_{2}\right) \geq \cos \left(\theta_{1}\right)+m\end{array}$

因此，$\cos \left(\theta_{1}\right)$ 被最大化，而 $\cos \left(\theta_{2}\right)$ 被最小化，使得 $C_{1}$ 执行大边际分类。$\text{Figure 2}$ 中 $\text{LMCL}$ 的决策边界，可以在角度余弦分布中看到一个清晰的 $\text{Margin}$( $\sqrt{2} m$)。这表明 LMCL 比 NSL 更健壮，因为在决策边界（虚线）周围的一个小的扰动不太可能导致不正确的决策。余弦裕度一致地应用于所有样本，而不考虑它们的权值向量的角度。

2.3 特征归一化

特征归一化的必要性包括两个方面：

• • 没有归一化之前的 $\text{Softmax}$ 损失函数会潜在地学习特征向量的 $L_{2}$ 模长和角度余弦。由于 $L_{2}$ 模长的增大，会一定程度上降低损失函数的值，这样会削弱余弦约束；
  • 同时希望所有数据的特征向量都具有相同的二范数，以至于取决于余弦角来增强判别性能。在超球面上，来自相同类别的特征向量被聚类在一起，而来自不同类别的特征向量被拉开；

比如假设特征向量为 $\mathrm{x}$，让 $\cos \left(\theta_{i}\right)$ 和 $\cos \left(\theta_{j}\right)$ 代表特征与两个权重向量的余弦，如果没有归 一化特征，损失函数会促使 $\|x\|\left(\cos \left(\theta_{i}\right)-m\right)>\|x\|\left(\cos \left(\theta_{j}\right)\right)$ ，但是优化过程中如果 $\left(\cos \left(\theta_{i}\right)-m\right)<\cos \left(\theta_{j}\right)$ ，为了降低损失函数，用 $\|x\|$ 的增加来换取损失函数的降低也是很可能的，所以会导致优化问题产生次优解。
此外尺度参数 $s$ 应该设置足够大，对于 NSL，太小的 $s$ 会导致收敛困难甚至无法收敛。在 LMCL，我 们需要设置更大的 $s$ 才能保证在预设的 Margin 以及在足够大的超球面空间来学习特征。
接下来分析 $s$ 应该有一个下界来保证获得期望的分类性能。给定归一化的学习特征向量 $x$ 和单位权重向量 $W$，用 $C$ 表示类别总数，假设学习到的特征分别位于超平面上，以相应的权重向量为中心。$p_{W}$  表示类里面期望的最小的后验概率(也就是与 $W$ 重合的特征的后验概率)， $s$  下界为:

$s \geq \frac{C-1}{C} \log \frac{(C-1) P_{W}}{1-P_{W}}  \quad\quad(6)$

可以分析出，如果在类别数保持一定情况下，想要得到最佳的 $p_{W}$，$\mathrm{~s}$ 要足够大。此外，如果固定 $p_{W}$，随着类别数的增加，也需要增大 $\mathrm{s}$ 值，因为类别数的增加会提升分类的难度。

2.4 LMCL的理论分析

选择合适的 $\text{Margin}$ 很重要，分析超参数 $\text{Margin}$ 的理论界限很有必要。

考虑二分类问题，类别分别是 $\mathrm{C}_1$  和 $\mathrm{C}_2$，归一化特征为 $x$，归一化权重向量 $W_{i}$，$W_{i}$ 与 $x$ 之间的夹角为 $\theta_{i}$，对于NSL而言，决策边界 $\cos \left(\theta_{1}\right)=\cos \left(\theta_{2}\right)$ 等同于 $W_{1}$ 和 $W_{2}$ 的角平分线。对于 $\mathrm{LMCL}$，对于 $\mathrm{C}_1$ 类样本它会驱使决策边界 $\cos \left(\theta_{1}\right)-m=\cos \left(\theta_{2}\right)$ 的形成，这样会导致  $\theta_{1}$ 比 $\theta_{2}$ 小的多。因此类间差异扩大，类内差异缩小。

我们发现 Margin 与 $W_{1}$ 和 $W_{2}$ 之间的角度有关系。当 $W_{1}$ 和 $W_{2}$ 都给定的时候，余弦 Margin 具有范围的限制。具体而言，假设一个场景，即属于第 $i$ 类的所有特征向量与第 $i$ 类的相应权重向量 $W_{i}$ 完全重叠。 换句话说，每个特征向量都与类 $i$ 的权重向量相同，并且显然，特征空间处于极端情况，其中所有特征向量都位于其类中心，在这种情况下，决策边界的 Margin 已最大化（即，余弦 Margin 的严格上限）。

理论上 $m$ 的范围是: $0 \leq m \leq\left(1-\max \left(W_{i}^{T} W_{j}\right)\right), i \neq j$ ，$\text{softmax}$ 损失尝试使来自任意两个类的两个权重之间的角度最大化，以执行完美分类。很明显，softmax 损失的最佳解决方案应将权重向量均匀分布在单位超球面上。引入的余弦 Maging 的可变范围可以推断如下:

$\begin{array}{l}0 \leq m \leq 1-\cos \frac{2 \pi}{C}, \quad(K=2) \\0 \leq m \leq \frac{C}{C-1}, \quad(C \leq K+1) \\0 \leq m \ll \frac{C}{C-1}, \quad(C>K+1)\end{array}   \quad\quad(7)$

$C$ 是训练类别数，$K$ 是学习特征的维度。这个不等式意味着随着类别数目越多，$\text{Margin}$ 的设置上界相应减少，特别是类别数目超过特征维数，这个上界允许范围变得会更小。在实践中 $m$ 不要取理论上界，理论上界是一种理想的情况（所有特征向量都根据相应类别的权重向量居中在一起），这样当 $m$ 太大模型是不会收敛的，因为余弦约束太严格，无法在现实中满足。其次过于严格的余弦约束对噪声数据非常敏感，影响整体性能。

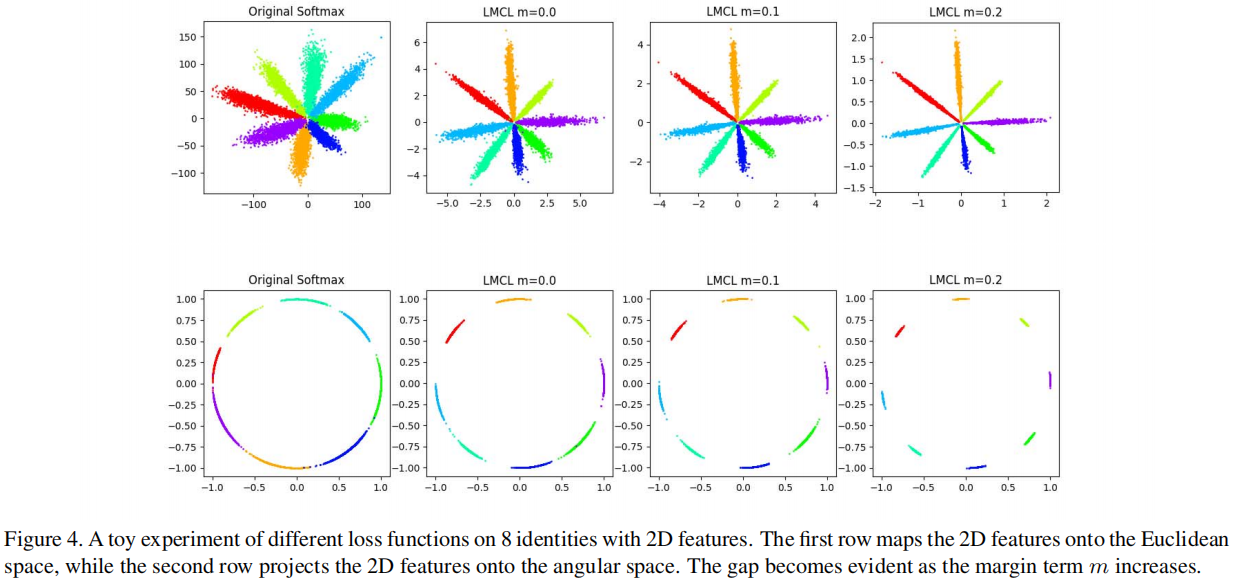
作者做了一个小实验验证了这些思想，取了 8 个人的人脸数据，用原始的 $\text{Softmax}$ 损失和本文提出的 LMCL 损失函数训练样本，然后将特征提取并可视化，$m$ 应该小于 $1-\cos \left(\frac{2 \pi}{8}\right)$，大约 $0.29$ ，分 别设置 $ \mathrm{m}=0,0.1,0.2$  三种情况，可以观察到原始的 $\text{softmax}$ 损失在决策边界上产生了混淆，而提出的 LMCL 则表现出更大的优势。随着$m$ 的增加，不同类别之间的角度 $\text{Margin}$ 已被放大。