论文信息

论文标题：Domain Confused Contrastive Learning for Unsupervised Domain Adaptation
论文作者：Quanyu Long, Tianze Luo, Wenya Wang and Sinno Jialin Pan

论文来源：
NAACL 2023
论文地址：
download
论文代码：download
视屏讲解：click

1 介绍

引入：

• 监督对比学习不适用于 NLP 无监督域适应，因为存在语法差异、语义偏移；

Note：
域差异较大：对比于图像之间的域差异，文本之间的域差异相对较大；

• 从领域适应的角度来看，构建跨域正样本和对齐域不可知对在相关文献中得到的重视较少；
  
  • 跨域正样本对齐：对比学习中的正采样减少了域差异；
  • 对齐域不可知：即下文提到的将源域、目标域和领域谜题 对齐；

提出：

• • 领域谜题（domain puzzle）：丢弃与领域相关的信息来混淆模型，因此很难区分这些谜题属于哪个领域；

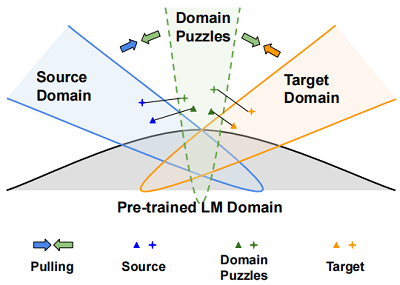
• • Fig 1：领域谜题可被认为是中间域，目的是使源样本和目标样本更接近，并通过学习域不变表示来连接两个域；

建议：

• • 不建议在源域和目标域之间直接寻找匹配的句子，而是利用源（目标）数据及其相应的领域谜题来减少域的差异，如 Fig1 所示。

• • 制作领域谜题的一个简单想法是屏蔽特定于领域的 Token，然而，Token 级的操作过于离散和不灵活，无法反映自然语言中的复杂语义变化。因此，本文的目标是寻找更好的领域谜题，在每个训练实例的表示空间中保持高置信度的预测和任务辨别能力；

2 相关工作

2.1 对抗训练

域对抗训练已经被证明可以提高很多自然语言模型的性能，这类算法通常考虑对单词嵌入的扰动，并减少输入样本周围的对抗损失，对抗训练的目标是：

$\underset{\theta_{f}, \theta_{y}}{\text{min}}\sum\limits _{(x, y) \sim \mathcal{D}}\left[\max _{\delta} \mathcal{L}\left(f\left(x+\delta ; \theta_{f}, \theta_{y}\right), y\right)\right]$

标准的对抗训练可用通过使用虚拟对抗训练进行正则化：

$\begin{array}{r}\underset{\theta_{f}, \theta_{y}}{\text{min}} \sum_{(x, y) \sim \mathcal{D}}[\mathcal{L}(f(x ; \theta_{f}, \theta_{y}), y)+\alpha_{a d v}\underset{\delta}{\text{max}} \mathcal{L}(f(x+\delta ; \theta_{f}, \theta_{y}), f(x ; \theta_{f}, \theta_{y}))]\end{array}$

内部最大化可以通过投影梯度下降（PGD）来求解，对抗性扰动 $\delta$ 的近似：

$\delta_{t+1}=\Pi_{\|\delta\|_{F} \leq \epsilon}\left(\delta_{t}+\eta \frac{g_{y}^{a d v}\left(\delta_{t}\right)}{\left\|g_{y}^{a d v}\left(\delta_{t}\right)\right\|_{F}}\right)$

$g_{y}^{a d v}\left(\delta_{t}\right)=\nabla_{\delta} \mathcal{L}\left(f\left(x+\delta_{t} ; \theta_{f}, \theta_{y}\right), y\right)$

其中，$\Pi_{\|\delta\|_{F} \leq \epsilon}$ 在 $\epsilon$ 球上执行投影。PGD 的优点在于它只依赖于模型本身来产生不同的对抗性样本，使模型能够更好地推广到不可见的数据。

3 方法

整体框架：

该模型将以源标记和未标记的目标句子作为输入。然后，它将通过制造对抗性扰动来增加输入数据。下一步用一个编码器生成一个隐藏表示，该编码器将进一步用于产生三个损失来训练整个模型，即情绪分类损失、对比损失和一致性损失。

3.1 制作领域谜题

对于 UDA，Saito等人[2017] 提到，简单地匹配分布并不能确保没有目标标签的目标域的高精度。此外，它还可能导致负转移，恶化知识从源域向目标域的转移。即使匹配的句子具有相同的标签，由于巨大的句法和语义转移，基于实例的匹配策略对齐来自不同域的例子，也会为预先训练的语言模型引入噪声，例如在 Fig3 中对齐源域和目标域句子。

或者，我们也可以定位和屏蔽与句子主题和类型相关的领域特定的标记。由于 Fig3 中绿色框中的句子成为领域不可知的，我们将那些领域混淆的句子（无法判断这些句子属于哪个领域）称为领域谜题。将源域与域难题以及目标域和域难题之间的匹配分布，也将使语言模型产生域不变表示。

然而，特定领域的标记并不总是明显的，由于自然语言的离散性，在不影响语义的情况下决定正确的标记是一个挑战，特别是当句子是复杂的。因此，我们在表示空间中寻找领域谜题，并引入对抗性扰动，因为我们可以依赖模型本身来产生不同但有针对性的领域谜题。请注意，这里的对抗性攻击的目的不是为了增强鲁棒性，而是为了构造精细产生的扰动，以便在表示空间中获得更好的域不变性。

为了生成域混淆的增强，我们采用带有扰动的对抗性攻击来进行域分类。使用对抗性攻击学习域分类器的损失可以指定如下：

$\begin{array}{l}\mathcal{L}_{\text {domain }}=\mathcal{L}\left(f\left(x ; \theta_{f}, \theta_{d}\right), d\right)+\alpha_{a d v} \mathcal{L}\left(f\left(x+\delta ; \theta_{f}, \theta_{d}\right), f\left(x ; \theta_{f}, \theta_{d}\right)\right)\end{array}$

$\delta=\Pi_{\|\delta\|_{F} \leq \epsilon}\left(\delta_{0}+\eta \frac{g_{d}^{a d v}\left(\delta_{0}\right)}{\left\|g_{d}^{a d v}\left(\delta_{0}\right)\right\|_{F}}\right)$

3.2 学习域不变特征

在获得域难题后，简单地应用分布匹配将会牺牲从源域学习到的判别知识，而基于实例的匹配也会忽略全局域内信息。为了在没有目标标签的情况下学习情感方面的辨别性表征，我们建议通过对比学习来学习领域不变特征。

此外，对比损失鼓励正对彼此接近，而负对相距很远。具体来说，最大化正对之间的相似性学习基于实例的不变表示，最小化负对之间的相似性从全局视角学习均匀分布的表示，使聚集在任务决策边界附近的实例彼此远离。这将有助于增强学习模型的任务辨别能力。

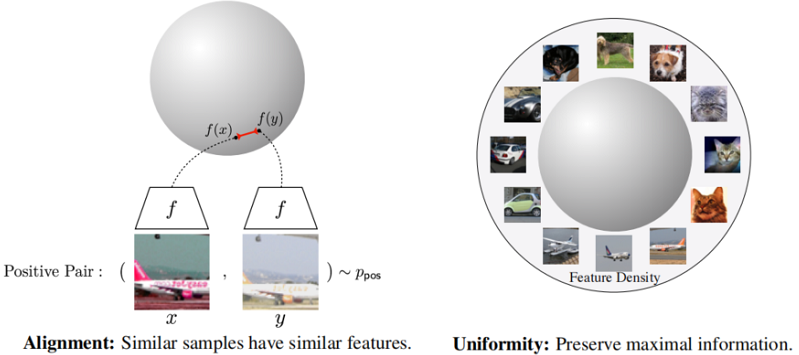
对于正采样，希望模型能够将原始句子和大多数具有领域挑战性的示例编码为在表示空间中更接近，随着训练的进行逐渐将示例拉到域决策边界。 对于负采样，它扩大了情感决策边界，并为两个领域提升了更好的情感判别特征。 然而，对于跨域负采样，对比损失可能会将目标（源）域中的负样本推离源（目标）域中的 anchor（见F ig4(b）左）。 这与试图拉近不同领域的领域谜题的目标相矛盾。

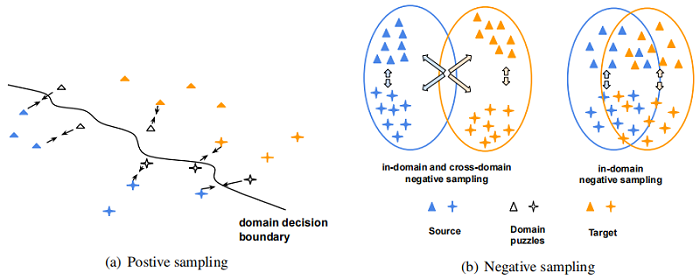
为了避免跨域排斥的损害，从负集中排除具有不同域的样本非常重要。修改后的 InfoNCE 损失：

$\mathcal{L}_{\text {contrast }}=-\frac{1}{N} \sum\limits _{i}^{N} \log \frac{\exp \left(s\left(z_{i}, z_{i}^{\prime}\right) / \tau\right)}{\sum_{k}^{N} \mathbb{1}_{k \neq i} \exp \left(s\left(z_{i}, z_{k}\right) / \tau\right)}$

其中 $N$ 是具有来自同一域的样本的小批量大小，$z_{i}=g\left(f\left(x_{i} ; \theta_{f}\right)\right)$，$g(\cdot)$ 是一个隐藏层投影头。 我们将 $x^{\prime}=x+\delta$ 表示为域拼图增强，$s(\cdot)$ 计算余弦相似度，$\mathbb{I}_{k \neq i}$ 是指示函数，$\tau$ 是温度超参数。

3.3 一致性正则化

给定基于域分类的扰动嵌入 $x+\delta$，我们还鼓励模型产生与原始实例 $f\left(x ; \theta_{f}, \theta_{y}\right)$ 一致的情感预测。

为此，我们最小化对称 $KL$ 散度，公式为：

$\mathcal{L}_{\text {consist }}=\mathcal{L}\left(f\left(x ; \theta_{f}, \theta_{y}\right), f\left(x+\delta ; \theta_{f}, \theta_{y}\right)\right)$

3.4 整体训练目标

对于整体训练目标，我们以端到端的方式训练神经网络，损失加权和如下。

$\begin{array}{l}\min _{\theta_{f}, \theta_{y}, \theta_{d}} \sum_{(x, y) \sim \mathcal{D} S} \mathcal{L}\left(f\left(x ; \theta_{f}, \theta_{y}\right), y\right)+\sum_{(x, y) \sim \mathcal{D}^{S}, \mathcal{D}^{T}}\left[\alpha \mathcal{L}_{\text {domain }}+\lambda \mathcal{L}_{\text {contrast }}+\beta \mathcal{L}_{\text {consist }}\right] \end{array}$

4 实验

参数敏感实验

可视化分析

5 总结

略