聊聊简单又不简单的图上多跳过滤查询
摘要:
多跳查询能力也是一个衡量产品性能非常重要的指标。
本文分享自华为云社区《
聊聊超级快的图上多跳过滤查询
》,作者:弓乙。
在图数据库/图计算领域,多跳查询是一个非常常用的查询,通常来说以下类型的查询都可以算作是多跳过滤查询:
1.查询某个用户的朋友认识的朋友 --二跳指定点label的查询2.查询某个公司的上下游对外投资关系 --N跳指定方向过滤查询3.查询某个公司实际持股股东 --N跳内带过滤查询4.搜索可提供某个零部件的供货商 --N跳内带过滤的until查询5.局点变更影响分析 --N跳内带过滤查询
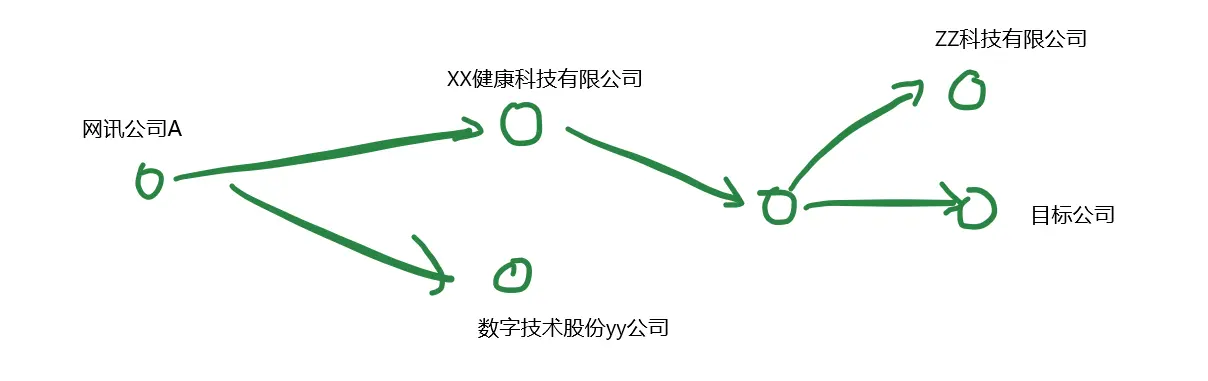
如下图,可用3跳查询得到网讯公司A所有的对外投资机构。
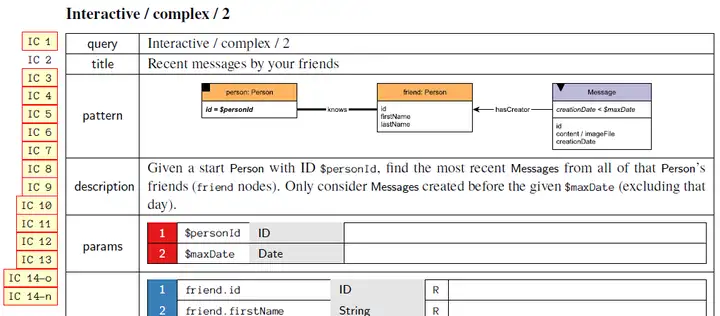
与此同时,多跳查询能力也是一个衡量产品性能非常重要的指标,比如LDBC(Linked Data Benchmark Council)的交互式查询场景下就设计了多个考察图数据库系统多跳查询能力的测试用例,交互式查询Interactive的Complex Query中有多个用例均为多跳查询,如下图是一个查朋友最近发送的消息的IC2用例,是一个经典的图上2-hop查询。
在图计算的尺度里,多跳过滤某些情况下被称为k-hop算法,BFS,DFS算法,区别仅在于traversal的策略是深度优先还是广度优先。
而在图数据库中一般将多跳过滤看做是
需要特殊优化
的模式匹配查询(cypher)或可组合的复合查询(gremlin)。
以下展示常用的图查询语言gremlin/cypher的二跳查询的写法,结果均为返回李雷朋友的朋友:
gremlin: g.V('李雷').out('朋友').out('朋友')
cypher: match (n)-->(m1:朋友)-->(s1)-->(m2:朋友)-->(s2) where id(n)='李雷' return s2
这两个语句
轻盈又直观
,看起来一切都被解决地如此优雅。
但事实真的如此吗?
很遗憾,当我们兴致勃勃地构图,将数据导入图数据,再使用类似上述语句查询实际业务场景时,你也许会惊讶地发现,也许结果与我们所期待的并不一致。
接下来,我将展开说说为什么使用多跳过滤查询会比我们想象中的更复杂,了解了图上遍历的概念后,我们能把而基于多跳过滤这一特性,我们又能怎么做使得这个重要的查询又快又流程呢?
功能那些事儿
上面我们介绍了查询一个用户朋友的朋友的例子,这里我们假设业务场景是向李雷推荐好友,思路是:向他推荐其好友的好友,但是
推荐的好友中不应包含李雷本身的好友
,比如图中小明同时是李雷的一跳好友和二跳好友。这时我们不应向李雷推荐小明,因为她已经是李雷的好友了。
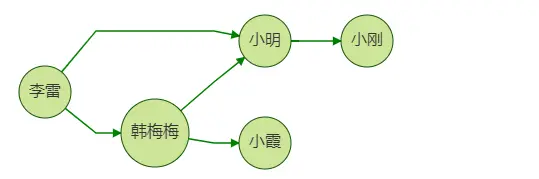
仅仅增加了一个返回的二跳邻居不包含一跳邻居这个条件,让我们来看下与上面单纯的2跳查询的gremlin和cypher变成什么样了?
gremlin:
g.V("李雷").repeat(out("朋友").simplePath().where(without('1hop')).store('1hop')).
times(2)
cypher:
match (a)-[:朋友]->(d) where id(a)='李雷' with a, collect(d) asneighbor
match (a)-[:朋友]-(b)-[:friend]-(c)where not (c inneighbor)return c
不知道各位有什么感觉?如果是不熟悉图查询语言的朋友们看到这里一定两眼发黑了吧哈哈。
不用担心,如果我们灵活使用一些特性,也许事情会变得简单,比如这是一个GES原生API多跳过滤查询Path Query的json请求:
{"repeat": [{"operator": "outV"}],"times": 2,"vertices": ["李雷"],"strategy":"ShortestPath"}
假如我们可以把它翻译为gremlin的写法的话,它大概是:
g.V('李雷').repeat(out()).times(2).strategy('ShortestPath')
以上的写法除了strategy('ShortestPath')其他本身就是gremlin已经支持的语法,意为
-查询从李雷出发以ShortestPath为遍历策略的二跳邻居。
遍历策略是什么?
理解遍历策略是了解
多跳过滤
的基石,我们这里从图论里几个定义展开:
A walk is a finite or infinite sequence of edges which joins a sequence of vertices.[2]
Let G= (V, E, ϕ) be a graph. A finite walk is a sequence of edges (e1, e2, …, en − 1) for which there is a sequence of vertices (v1, v2, …, vn) such that ϕ(ei) = {vi, vi + 1} for i = 1, 2, …, n − 1. (v1, v2, …, vn) is the vertex sequence of the walk. The walk is closed if v1 = vn, and it is open otherwise. An infinite walk is a sequence of edges of the same type described here, but with no first or last vertex, and a semi-infinite walk (or ray) has a first vertex but no last vertex.
A trailis a walk in which all edges are distinct.[2]
A pathis a trail in which all vertices (and therefore also all edges) are distinct
以上应用wiki中对于图上不同的点集组成的边集说明,详情见Path (graph theory) - Wikipedia。
以下,我将几个相似又不同的概念用四个维度区分开。
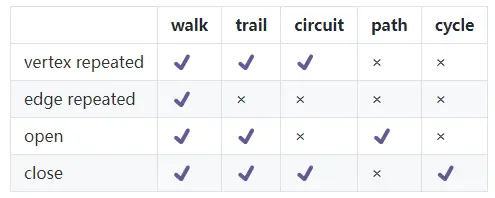
以上5个概念均指代在G=(V,E,φ)中,由点V,边E组成的序列。
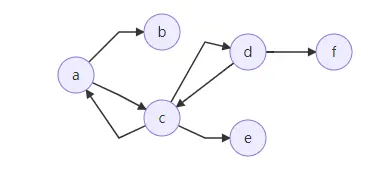
上图中,对于序列a->c->d->f,我们可以将它称为walk, trail, path,三者都可以。因为该序列的起点a与终点f不同,不属于对序列要求close状态circuit和cycle。
而序列a->c->a->c, 我们只能将其归为walk。因为其不闭合不属于circuit和cycle,且点有重复(a,c两个都有重复)不属于path,边集有重复(a->c的边有重复)不属于trail。
遍历策略对
最终的结果和遍历效率
都有决定性的影响。

这里简单说明下新增的shortestPath策略:
- Walk:以图论中划定的walk进行图遍历:即在traversal的过程中允许经过重复的点和重复的边。
- ShortestPath:以shortestPath的规则进行图遍历:即在BFS traversal的过程不会遍历在前面跳数出现过的点。在这种模式下的路径每个终点到起点都是最短路径。
BFS与DFS
影响遍历顺序的另一个角度一般我们分为:
- BFS - Breadth-first search 广度优先搜索
- DFS - Depth-first search 深度优先搜索
BFS在图遍历时会优先遍历一个点的所有邻居,再遍历其邻居的邻居,而DFS会优先遍历点的邻居的邻居,直到到达最深的节点。
我们可以设置一个batchSize,表示在进行BFS时不遍历全部的邻居,而是每层以batchSize的数量进行遍历,然后再以batchSize的个数遍历下一层邻居。
可以推断出,当batchSize=1时,该BFS约等于DFS的遍历策略。
性能那些事儿
多跳过滤的性能受很多因素影响。以下总结一些会影响到性能的因素以供参考:

而对于不同规模的图,多跳过滤查询的TPS大部分情况下并不取决于图的点边规模,而是与图的密度密切相关。
比如一个二跳查询,那么TPS就与该图的二跳邻居分布强相关。
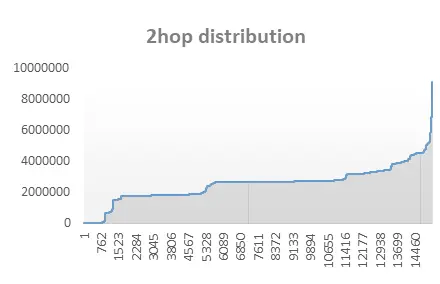
简单来讲,多跳过滤最终的性能主要受
遍历过程中触达节点的个数影响
。同样规模的图,其多跳过滤tps可能相差很大。大部分情况下基准测试仅提供横向比较,考验的是图数据库/图引擎本身的性能指标,有一定参考价值,但仍以实际业务图表现为主。
经验上,稀疏的图性能表现大大好于稠密的图。
多跳查询的使用
为了简化多跳过滤查询的表达,我们用一些参数来表达查询过程。如前面章节介绍过的遍历策略,batchSize等。
本章我们将一一介绍以下特性参数:

接下来我们以GES的path query(filterquery version2版本)接口来举例介绍多跳过滤查询的使用。
该接口支持对
多跳过滤查询,循环执行遍历
查询进行加速。可以看做是gremlin的repeat语句的扩充表达,例如以下gremlin语句:
g.V('1','2').repeat(out()).times(2).emit().dedup()
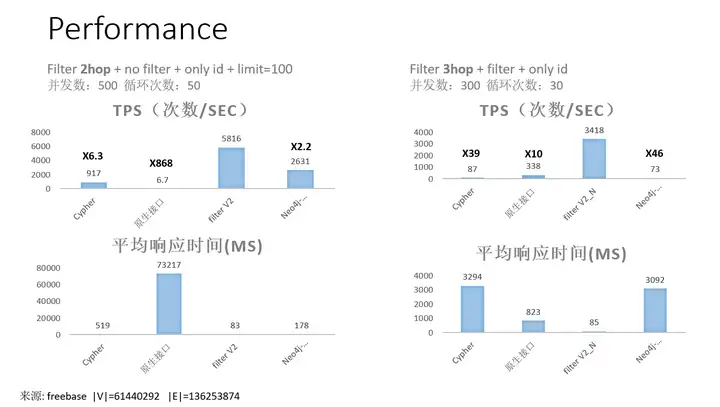
以下为该接口的2跳/3跳查询在1亿规模图上的测试情况。
其中,
- filterV2 - GES
的多跳过程查询原生接口,该API性能最佳,TPS与延迟表现优异。 - Cypher - GES
的cypher查询(较老版本)。 - Neo4j - Neo4j
community 4.2.3版本cypher。 - gremlin - GES
的gremlin,未在图中体现,实际性能最差,故未做对比。
请求样例1
POST /ges/v1.0/{projectId}/graphs/{graphName}/action?action_id=path-query
{"repeat": [{"operator": "outV"}
],"emit": true,"times": 2,"vertices": ["1","2"]
}
以上请求等价于gremlin语句:
g.V('1','2').repeat(out()).times(2).emit().dedup()####
特性参数简要说明
速查参数表
filterV2的参数过于复杂,需要花一定的时间去理解?请看下面总结出的速查表,帮助您快速使用repeat模式:
PS:strategy策略的说明查看下方
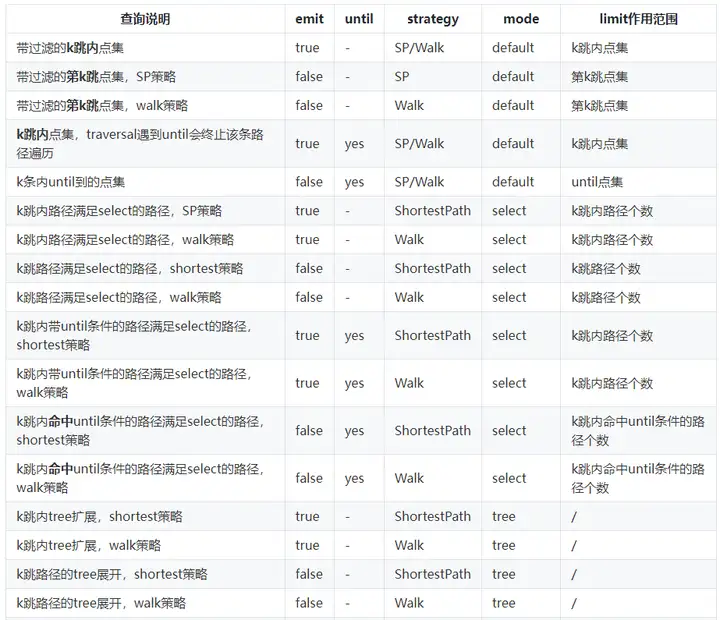
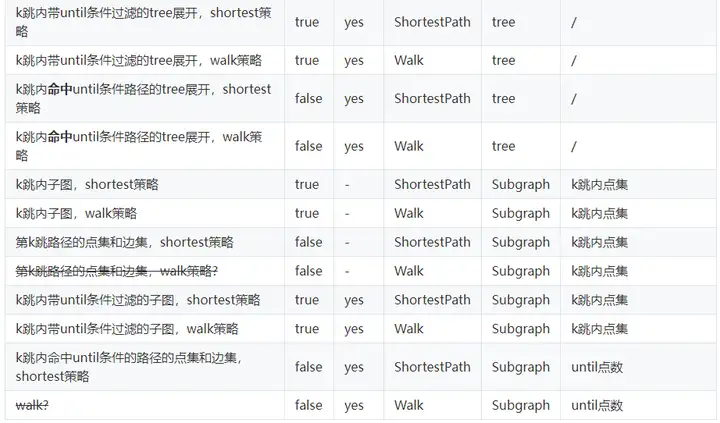
emit模式
emit是一个filtered query参数中对其他各个参数影响最大的参数。我们将其定义为,是否输出query过程中的点,其含义也与gremlin中的emit一致。
下面将介绍,在不同模式下emit的表现形式:
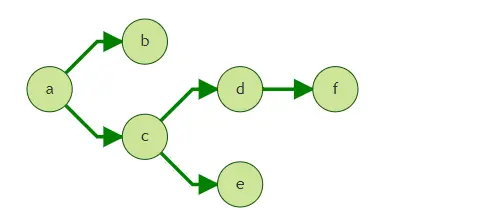
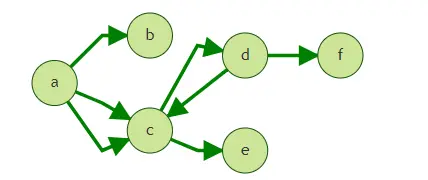
上图中,假定我们从点a出发,执行filtered khop query的查询。
strategy
图遍历过程中使用的策略,目前可选:ShortestPath和Walk。
- Walk:以图论中划定的walk进行图遍历:即在traversal的过程中允许经过重复的点和重复的边。
- ShortestPath:以shortestPath的规则进行图遍历:即在BFS traversal的过程不会遍历在前面跳数出现过的点。在这种模式下的路径每个终点到起点都是最短路径。
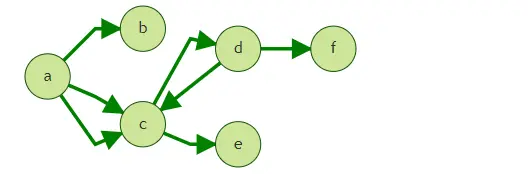
上图中,假定我们从点a出发,执行query的4跳查询。
Walk: a->c->a->b, a->c->a->c, a->c->d->f, a->c->d->c
ShortestPath: a->c->d->f
简单查询
1. 查询从a出发的第三跳邻居
使用gremlin查询:
g.V('a').out().out().out()
g.V('a').repeat(out()).times(3)
以上两种写法是等效的,结果为点f。路径为a->c->d->f。
对应在API参数为:
{"repeat": [
{"operator": "outV"}
],"emit": false,"times": 3,"vertices": ["a"]
}
2. 查询从a出发的三跳内邻居
使用gremlin查询:
g.V('a').repeat(out()).times(3).emit()
结果为b,c,d,e,f。
对应在API参数为:
{"repeat": [
{"operator": "outV"}
],"emit": true,"times": 3,"vertices": ["a"]
}
组合模式说明
emit+strategy
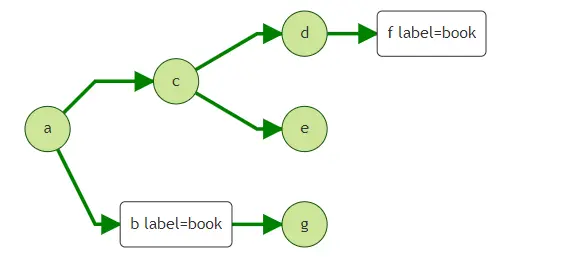
1. 查询第三跳邻居
在上面的图中,如果按照[简单查询1](#1. 查询从a出发的第三跳邻居), 将得到点f, c, b。
路径为a->c->a->b, a->c->d->f, a->c->d->c。
如果,我们只想得到f, 而不希望取到前两跳已经出现过的点c和b。则需要使用strategy模式中的ShortestPath。ShortestPath模式保证API在traversal的过程中起始点到各点是最短路径。该模式能够有效降低多跳查询中指数增长的查询量。
gremlin的写法为:
g.V("a").repeat(out().simplePath().where(without('hops')).store('hops')).times(3).path()
结果为仅为a->c->d->f。
对应在API参数为:
{"repeat": [
{"operator": "outV"}
],"emit": false,"strategy": "ShortestPath","times": 3,"vertices": ["a"]
}
emit+until
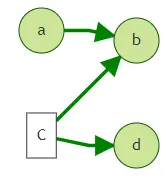
1.提前终止traversal模式说明
我们以上面的图来说明该模式,当我们不清楚查询需要经过多少跳,但希望通过某些条件提前终止遍历,可以用到until。
如以下两个问题:
1.得到从a出发N跳内label=book的点。2.得到从a出发N跳内所有点,停止查询的条件为遇到label=book的点。
以上问题可以配合emit参数来解决,用gremlin可以写为:
Q1: g.V('a').repeat(out()).until(hasLabel('book'))
Q2: g.V('a').repeat(out()).until(hasLabel('book')).emit()
与之对应的API为:
{"repeat": [
{"operator": "outV"}
],"until": [
{"vertex_filter": {"property_filter": {"leftvalue": {
“label_name":""},"predicate": "=","rightvalue": {"value": "book"}
}
}
}
],"emit": false/true,//这里根据Q1,Q2的情况选择emit的值。 "times": 5,"vertices": ["a"],"strategy": "Walk"}
repeat模式说明
repeat+times
可通过参数repeat+times实现多种形式的多跳过滤及repeat模式过滤。
1.仅多跳过滤
gremlin的写法为:
g.V("a").repeat(out().in()).times()
或
g.V("a").out().in()
对应在API参数为:
{"repeat": [
{"operator": "outV"},
{"operator": "inV"}
],"strategy": "Walk","times": 2,"vertices": ["a"]
}
2.repeat mode
假如我们从点a出发,查询其带方向的四跳邻居。即:
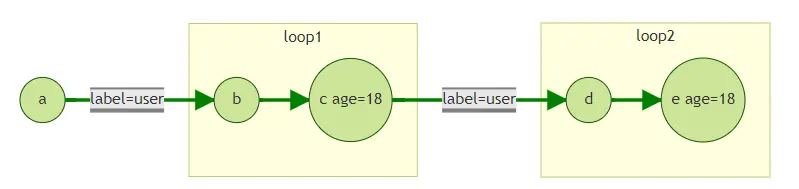
gremlin的写法为:
g.V('a').repeat(out('user').out().has('age',18)).times(2)
或
g.V('a').out('user').out().has('age',18).out('user').out().has('age',18)
对应在API参数为:
{"repeat": [
{"operator": "outV","edge_filter": {"property_filter": {"leftvalue": {"label_name": ""},"predicate": "=","rightvalue": {"value": "user"}
}
}
},
{"operator": "outV","vertex_filter": {"property_filter": {"property_name": {"label_name": "age"},"predicate": "=","rightvalue": {"value": "18"}
}
}
}
],"times": 4,"emit": false,"vertices": ["a"]
}
by模式说明
by模式当前支持两种形式:
- select+by mode
- by mode
by mode
该模式可针对输出的点进行输出格式上的过滤,返回的格式形如:
{"data": {"vertices": [
{"id": "47","label": "user"},
{"id": "51","label": "user"}
]
}
}
例如针对二跳邻居,我们可以通过参数by对id,label,property进行过滤:
g.V("a").repeat(out()).times(2).by(id())
转化为filtered query V2的形式为:
{"repeat": [
{"operator": "outV"}
],"times": 2,"vertices": ["a"],"by": [{"id": true}]
}
select + by mode
该模式可任意选择traverse路径上经过的N层。但每层只能在by中指定一个输出,返回的格式形如:
{"select": [
["李雷", "小明","小智"],
["李雷","韩梅梅", "小智"],
["李雷", "韩梅梅", "小霞"]
]
}
下面我们来介绍一下select+by模式。如下图,我们希望返回李雷的二跳邻居的路径情况。
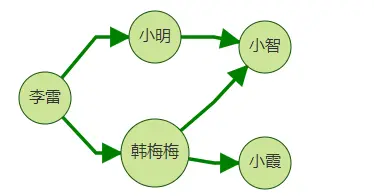
{"repeat": [
{"operator": "outV"}
],"times": 2,"vertices": ["李雷"],"by": [{"id": true},{"id": true},{"id": true}],"select": ["v0", "v1", "v2"]
}
g.V('1').as('v0').both().as('v1').both().as('v2').select('v0','v1','v2').by(id()).select(values)
在上面body体中,我们使用select自带的隐含层数别名v0, v1, v2。其分别表示
用户输入的点集第0层-v0, K跳中的第1层-v1, K跳中的第2层-v2。
select中选中的别名与by中指定的格式一一对应。
以上案例输出格式形如:
{"select": [
["李雷", "小明","小智"],
["李雷","韩梅梅", "小智"],
["李雷", "韩梅梅", "小霞"]
]
}
当然,我们也可以有更多的更丰富的输出。比如我们希望将输入点李雷的id和label都展示在路径中,并且去掉了中间第一跳的好友小明和韩梅梅,直接显示李雷及其第二跳好友的关系:
{"repeat": [
{"operator": "outV"}
],"times": 2,"vertices": ["李雷"],"by": [{"id": true},{"label": true},{"id": true}],"select": ["v0", "v0", "v2"]
}
最终展示结果是对路径自动去重的。比如在这个例子中,李雷到小智有两条路径,中间分别经过好友小明和韩梅梅, 但最终仅显示了一条。
以上案例输出格式形如:
{"select": [
["李雷", "person", "小智"],
["李雷", "person", "小霞"]
]
}
案例
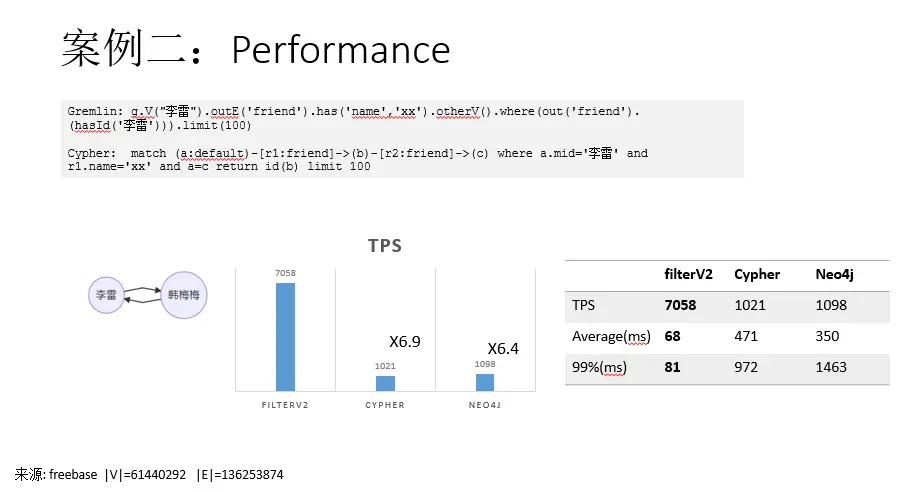
案例一.好友推荐
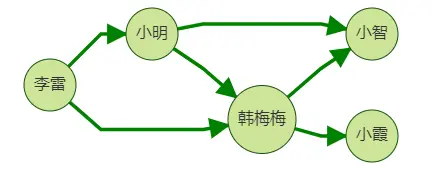
我们向李雷推荐好友,思路是:向他推荐其好友的好友,但是推荐的好友中不应包含李雷本身的好友,比如图中韩梅梅同时是李雷的一跳好友和二跳好友。这时我们不应向李雷推荐韩梅梅,因为她已经是李雷的好友了。
下面将分别展示使用gremlin,cypher和下一代filter query查询,返回均为推荐路径:李雷->李雷好友->推荐好友。
gremlin
gremlin>g.V("李雷").repeat(out("friend").simplePath().where(without('1hop')).store('1hop')).
times(2).path().by("name").limit(100)
gremlin>[李雷,小明,小智]
[李雷,韩梅梅,小智]
[李雷,韩梅梅,小霞]
cypher
match (a)-[:friend]->(d) where id(a)='李雷' with a, collect(d) asneighbor
match (a)-[:friend]-(b)-[:friend]-(c)where not (c inneighbor)returna.name, b.name, c.name
[
{"row": ["李雷", "小明","小智"],"meta": [null, null, null]
},
{"row": ["李雷","韩梅梅", "小智"],"meta": [null, null, null]
},
{"row": ["李雷", "韩梅梅", "小霞"],"meta": [null, null, null]
}
]
filtered query V2
{"repeat": [
{"operator": "outV","edge_filter": {"property_filter": {"leftvalue": {"label_name": "labelName"},"predicate": "=","rightvalue": {"value": "friend"}
}
}
}
],"times": 2,"vertices": ["李雷"],"by": [{"id": true},{"id": true},{"id": true}],"select": ["v0", "v1", "v2"]
}
{"select": [
["李雷", "小明","小智"],
["李雷","韩梅梅", "小智"],
["李雷", "韩梅梅", "小霞"]
]
}
案例二:自环写法案例
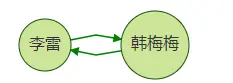
gremlin
gremlin>g.V("李雷").outE('friend').has('name','xx').otherV().where(out('friend').
(hasId('李雷'))).limit(100)
cypher
match (a:default)-[r1:friend]->(b)-[r2:friend]->(c) where a.mid='李雷' and r1.name='xx' and a=c return id(b) limit 100
reference
LDBC Social Network Benchmark (LDBC SNB)
从零开始学Graph Database(1)- 基础篇-云社区-华为云