全面掌握胶囊网络:从基础理论到PyTorch实战
本文全面深入地探讨了胶囊网络(Capsule Networks)的原理、构建块、数学模型以及在PyTorch中的实现。通过本文,读者不仅能够理解胶囊网络的基础概念和高级数学原理,还能掌握其在实际问题中的应用方法。
关注TechLead,分享AI与云服务技术的全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人。

一、引言
深度学习在最近几年取得了显著的进展,特别是在计算机视觉、自然语言处理和其他人工智能应用领域。尽管如此,当前的深度学习模型,尤其是卷积神经网络(CNNs)还存在一些局限性。例如,它们往往对输入的微小变化高度敏感,而且对于学习复杂的空间层次结构效率不高。正是为了解决这些问题,胶囊网络(Capsule Networks,CapsNets)应运而生。
胶囊网络是由 Geoffrey Hinton 教授等人于 2017 年引入的,旨在解决传统深度学习模型的一些根本性问题。与传统的深度网络相比,胶囊网络具有更强的能力去识别复杂的层次结构和空间关系,这对于很多实际应用场景来说是非常重要的。
本文将详细介绍胶囊网络的基础概念,从其背后的动机、核心构建块到数学原理等方面进行深入探讨。我们也会与卷积神经网络进行比较,以便更清晰地展示胶囊网络的优势。最重要的是,本文将提供一个使用 PyTorch 实现的胶囊网络的完整实战指南,包括代码段、注释以及相关输出。
二、胶囊网络的起源与动机
胶囊网络(Capsule Networks, CapsNets)是由 Geoffrey Hinton、Alex Krizhevsky 和 Ilya Sutskever 等人于 2017 年提出的。该网络模型的出现并非偶然,而是为了解决传统深度学习模型,特别是卷积神经网络(CNN)在某些方面存在的局限性。
动机:何为胶囊网络?
胶囊网络的设计初衷主要来自于解决两个问题:
局部敏感性
和
层次结构解析能力的不足
。
局部敏感性
:传统的 CNN 在图像识别任务中表现优秀,但它们对于输入的微小变化非常敏感。例如,稍微旋转或平移一个图像可能导致 CNN 的输出发生显著变化。层次结构解析能力的不足
:CNN 主要关注局部特征,并可能忽略这些特征如何在更高层次上组织成有用的结构。这就导致了它们在理解复杂空间层次关系方面的不足。
解决方案:胶囊与动态路由
胶囊网络引入了“胶囊”(capsule)的概念。每个胶囊都是一个小型的神经网络,它能够识别特定类型的视觉模式,并且对其存在的概率和姿态参数进行编码。通过这样的设计,胶囊能够保留更多的空间层次信息。
胶囊网络还引入了一种名为“动态路由”的机制。该机制能够在不同胶囊之间传递信息,从而使得网络能够更好地理解对象的内部组成结构和相对空间关系。
为何重要?
理解胶囊网络的动机不仅有助于我们更好地理解其工作原理,而且能让我们看到这一模型在处理一系列复杂任务时的潜力。例如,在医疗图像分析、自动驾驶以及高级监控系统中,对对象的几何结构和相对关系的理解是非常关键的。
三、胶囊网络的基础构建块
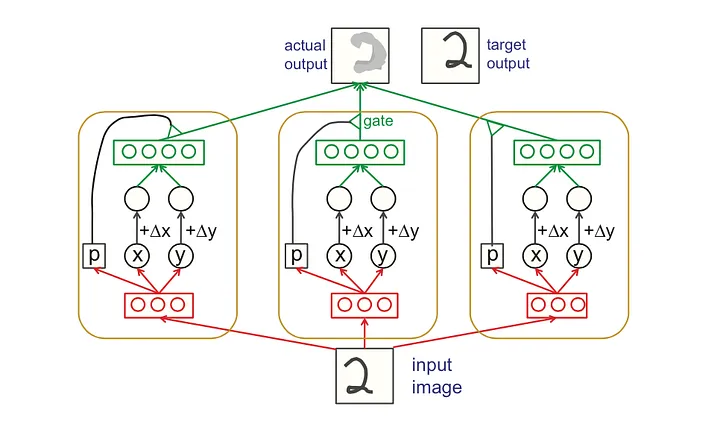
3.1 胶囊
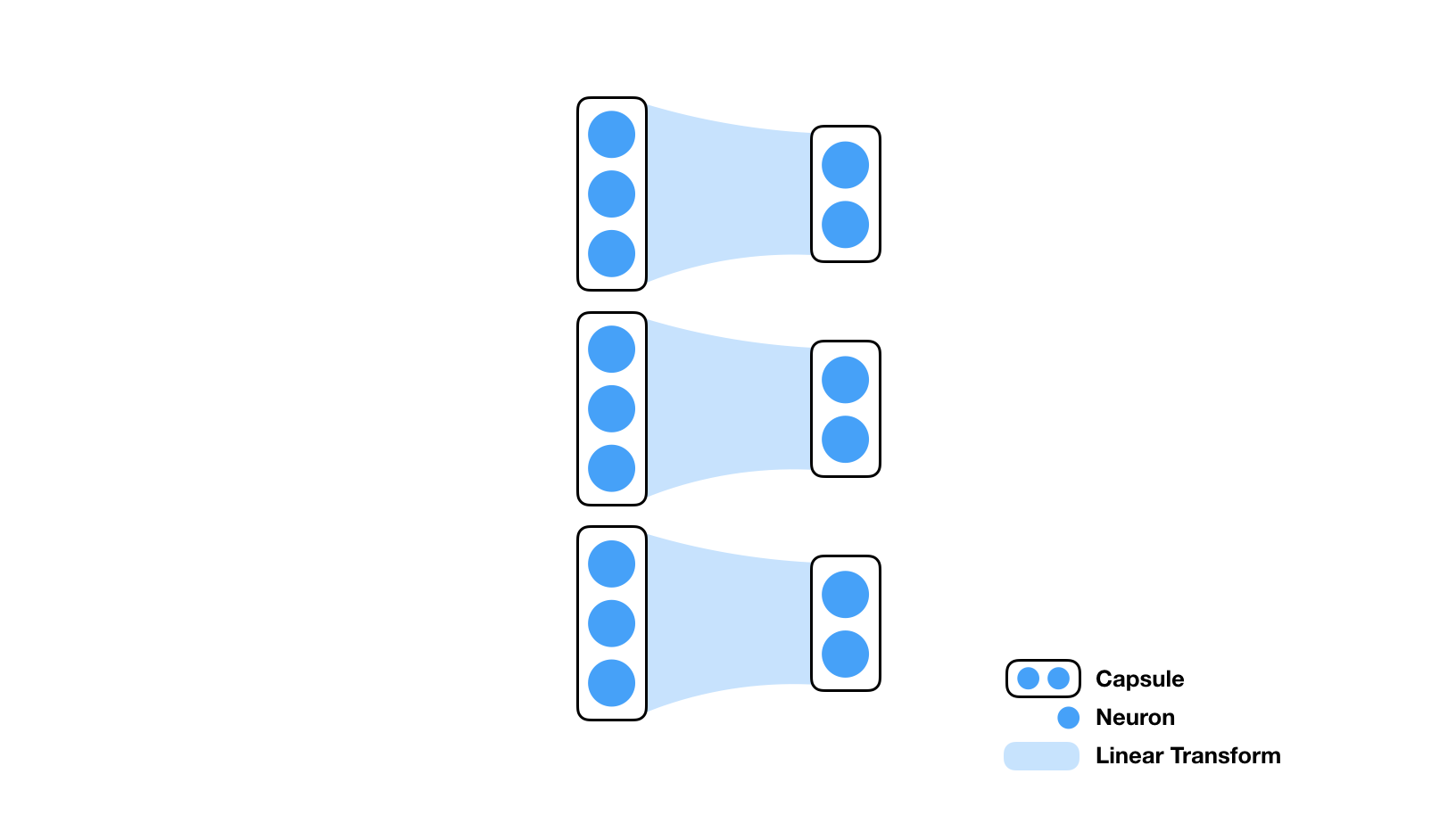
胶囊(Capsule)是胶囊网络(Capsule Networks, CapsNets)的核心组件,扮演着捕捉和编码复杂模式与层次结构信息的角色。与传统神经网络中的神经元相比,胶囊具有更高维度的输出和更复杂的内部结构,这使得胶囊能够对输入数据进行更为精细和丰富的描述。
高维输出向量
传统神经元的输出通常是一个标量,表示某一特定特征或属性的激活强度。与之不同,胶囊的输出是一个高维向量。这个输出向量的模长通常用于表示某种特定特征是否存在,而向量的方向则用于编码该特征的更多属性——如位置、方向、大小等。
# Python/PyTorch代码示例: 胶囊输出向量
import torch
# 模拟一个胶囊的输出向量
capsule_output = torch.Tensor([0.8, 0.1, 0.3])
# 输出向量的模长
magnitude = torch.norm(capsule_output)
print("Magnitude of the capsule output:", magnitude.item()) # 输出模长,表示特征出现的概率
# 输出向量的方向
direction = capsule_output / magnitude
print("Direction of the capsule output:", direction) # 输出方向,编码特征属性
局部不变性与局部可变性
在捕捉图像或其他类型数据的局部特征时,胶囊能够在保持局部不变性(例如,平移不变性)的同时,也保留局部可变性(如相对位置、大小等)。这种平衡性使胶囊特别适用于需要精细描述对象及其组成部分的应用场景。
信息编码与解码
胶囊不仅可以编码高级特征的存在与属性,还能通过解码这些高维向量来重构输入或进行更高层次的推断。
# Python/PyTorch代码示例: 使用胶囊输出进行信息解码
def decode_capsule_output(capsule_output):
# 这里仅作为一个示例,实际应用会更复杂
decoded_info = capsule_output * 2.0 # 假设解码过程
return decoded_info
decoded_info = decode_capsule_output(capsule_output)
print("Decoded information:", decoded_info)
数学基础与底层操作
胶囊通常涉及一系列底层数学运算,如“压缩”(squashing)函数用于限制输出向量的模长。这些运算与胶囊的具体应用和架构有关,但都旨在实现更为复杂和丰富的数据表示。
# Python/PyTorch代码示例: 压缩函数
def squash(vector):
norm = torch.norm(vector)
return (norm / (1.0 + norm ** 2)) * vector
squashed_output = squash(capsule_output)
print("Squashed output:", squashed_output)
3.2 动态路由
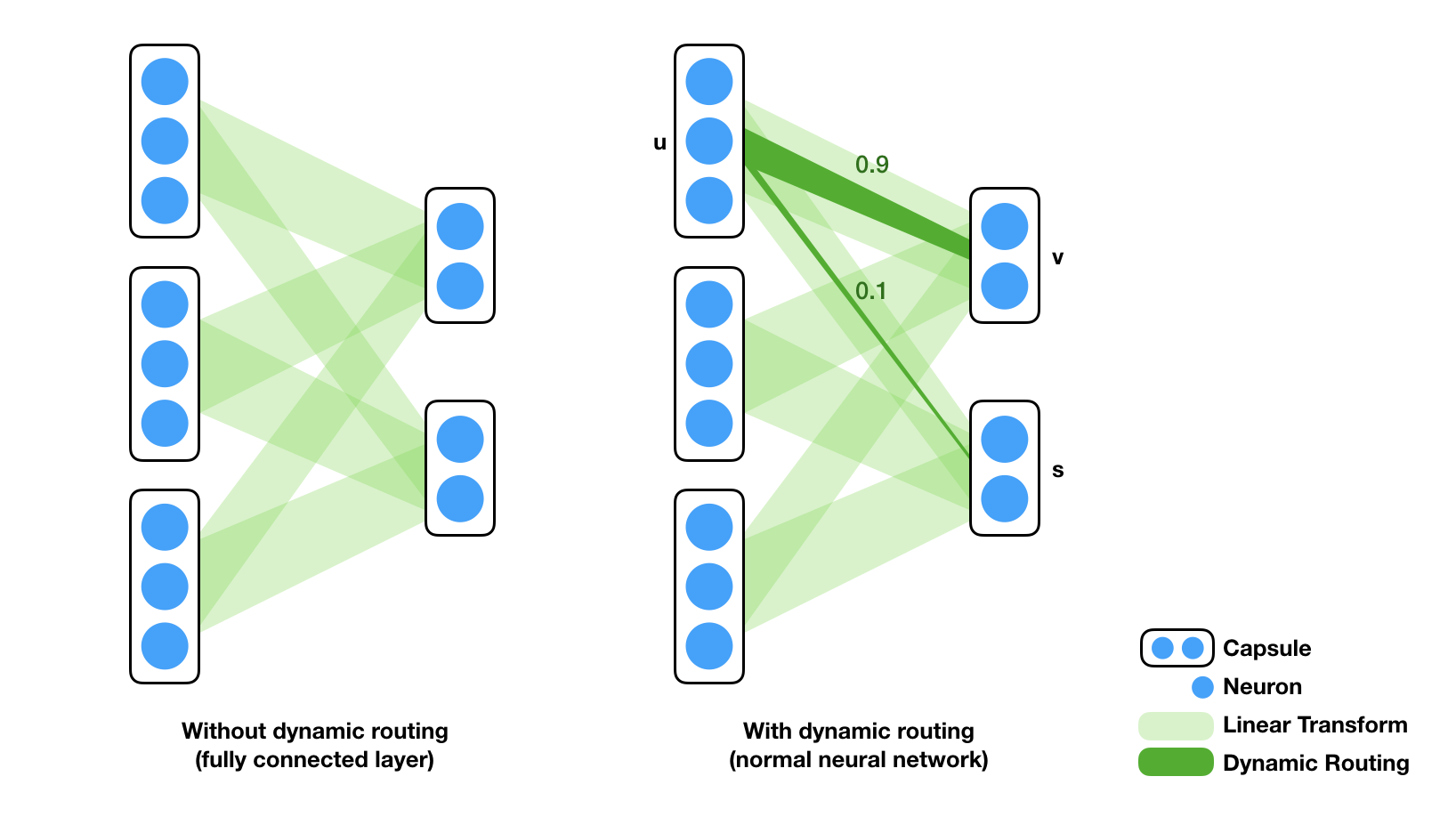
动态路由(Dynamic Routing)是胶囊网络中的一种关键算法,用于在不同层之间传递信息。相比于传统的前向传播机制,如卷积神经网络(CNN)中的最大池化(Max Pooling)操作,动态路由具有更高的灵活性和信息保留能力。
路由机制与权重更新
在动态路由中,下层胶囊的输出会被加权求和,以生成上层胶囊的输入。这个加权求和不是固定的,而是通过迭代算法动态更新的,使得网络可以自适应地确定哪些信息更应该被传递到上一层。
# Python/PyTorch代码示例: 动态路由
import torch
import torch.nn.functional as F
def dynamic_routing(lower_capsule_output, routing_iterations=3):
batch_size, lower_dim, _ = lower_capsule_output.shape
upper_dim = 10 # 假设上层胶囊有10个
# 初始化路由权重为0
b_ij = torch.zeros(batch_size, lower_dim, upper_dim)
for i in range(routing_iterations):
# 使用softmax计算每个下层胶囊到上层胶囊的权重(coupling coefficients)
c_ij = F.softmax(b_ij, dim=2)
# 计算上层胶囊的加权输入
s_j = (c_ij[:, :, None] * lower_capsule_output).sum(dim=1)
# 使用激活函数计算上层胶囊的输出(这里简化为ReLU)
v_j = F.relu(s_j)
# 更新路由权重
b_ij += (lower_capsule_output * v_j[:, None, :]).sum(dim=-1)
return v_j
# 模拟下层胶囊输出(batch_size=32, lower_dim=8, vector_dim=16)
lower_capsule_output = torch.rand(32, 8, 16)
# 运行动态路由算法
upper_capsule_output = dynamic_routing(lower_capsule_output)
算法优势与特性
- 信息丰富性
: 动态路由能够保留更多的结构信息,如物体的部件和层次关系。 - 参数效率
: 由于动态路由可以自适应地选择重要信息,它可以减少网络中不必要的参数。 - 鲁棒性
: 动态路由增加了模型对于输入变化(如平移、缩放)的鲁棒性。
从理论到实践
动态路由算法是Geoffrey Hinton等人在2017年首次提出的,至今已有多种改进和变种。在实践中,动态路由算法经常需要与特定的胶囊架构和任务相结合进行优化。
例如,一些研究通过引入注意力机制(Attention Mechanisms)进一步改善动态路由的性能。而在某些任务中,如图像分割,动态路由与卷积层或递归层的结合也有研究报道。
四、胶囊网络的数学原理
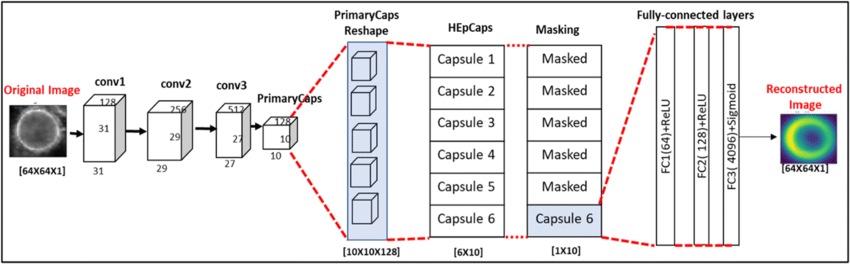
4.1 向量表示
胶囊网络与传统神经网络的一个重要区别在于其对信息的高维向量表示。这种高维向量不仅仅是一个简单的数值集合,它具有丰富的几何与数学内涵。本节将深入探讨这一向量表示的数学特性。
向量的角度与模长
在胶囊网络中,高维向量的模长(magnitude)通常用于表示某个特定特征出现的概率或强度,而向量的方向则编码了该特征的附加属性,如位置、旋转等。这种区分非常关键,因为它允许模型在一个统一的框架内同时处理“存在性”与“属性”。
数学表达如下:
[
\text{模长} = | \mathbf{v} |_2, \quad \text{方向} = \frac{\mathbf{v}}{| \mathbf{v} |_2}
]
旋转与变换
在胶囊网络中,高维向量经常需要进行一系列变换,这些变换通常通过矩阵乘法来实现。这些矩阵可视为一种“变换矩阵”,其作用类似于传统的仿射变换,但在高维空间中进行。
# Python/PyTorch代码示例: 向量变换
import torch
# 初始向量
initial_vector = torch.Tensor([0.8, 0.2])
# 变换矩阵
transformation_matrix = torch.Tensor([[0.9, -0.1], [0.1, 0.8]])
# 应用变换
transformed_vector = torch.matmul(transformation_matrix, initial_vector)
内积与相似度
在动态路由算法中,两个胶囊间的相似度常常用它们输出向量的内积来衡量。这种相似度计算能够有效捕获两个高维向量在空间中的相对位置和方向,从而为路由提供有用的参考信息。
[
\text{相似度} = \mathbf{u} \cdot \mathbf{v} = \sum_{i} u_i \times v_i
]
# Python/PyTorch代码示例: 内积计算
similarity = torch.dot(initial_vector, transformed_vector)
正交与子空间
在某些应用场景中,可以利用高维向量的正交性(orthogonality)来表示不同的、互斥的特征。比如,在自然语言处理中,不同词义的编码向量可能会被设计为相互正交,以减少歧义。
高级数学工具:流形学与信息几何
在更高级的胶囊网络研究中,流形学(Manifold Learning)和信息几何(Information Geometry)等数学工具也得到了应用。这些高级数学工具可以帮助我们更精确地描述和理解高维向量空间的复杂结构。
4.2 路由算法

动态路由算法是胶囊网络中至关重要的一部分,其工作方式与传统的神经网络中的前向传播算法有显著不同。该算法负责决定如何将底层胶囊的输出向量路由到更高层的胶囊,这一过程涉及到一系列复杂的数学运算。在本节中,我们将深入探讨动态路由算法的数学原理。
软路由与硬路由
在动态路由算法中,存在两种主要类型:软路由和硬路由。软路由通常基于“赋予权重”的概念,通过学习得到的参数来决定输出向量的组合;而硬路由则更为直接,通常通过一定的逻辑或决策树来确定路由。
数学上,软路由可以表示为:
[
\text{输出向量} = \sum_{i} c_i \mathbf{v}_i
]
其中 ( c_i ) 是权重系数,通常通过“注意力机制”或“聚合算法”来确定。
动态路由的迭代过程
动态路由算法通常采用迭代的方式进行。在每次迭代中,底层胶囊通过某种形式的“协商”来更新它们与上层胶囊之间的连接权重。
[
c_{ij} = \frac{\exp(b_{ij})}{\sum_k \exp(b_{ik})}
]
其中,(b_{ij}) 通常是一个“相似度得分”,可以通过底层和上层胶囊的输出向量的内积来计算。
# Python/PyTorch代码示例: 动态路由算法
import torch.nn.functional as F
# 相似度得分矩阵
b = torch.randn(10, 6) # 假设有10个底层胶囊和6个上层胶囊
# 更新路由权重
c = F.softmax(b, dim=1)
损失函数与优化
在动态路由算法中,损失函数通常涉及到多个方面,包括但不限于向量模长的损失、分类准确性损失以及路由稳定性损失。这些损失共同指导模型的优化过程。
[
\mathcal{L} = \alpha \mathcal{L}
\text{marg} + \beta \mathcal{L}
\text{class} + \gamma \mathcal{L}_\text{route}
]
其中,(\alpha, \beta, \gamma) 是超参数,用于平衡各项损失。
五、PyTorch实现胶囊网络
5.1 模型搭建
使用PyTorch实现胶囊网络涉及到多个关键步骤,其中包括定义底层和上层胶囊、实现动态路由算法,以及训练模型。在本节中,我们将侧重于模型的具体搭建过程。
定义胶囊层
首先,我们需要定义一个胶囊层,这通常由多个单独的胶囊组成。每个胶囊都是一个小型神经网络,可以通过标准的全连接层或卷积层来实现。
import torch
import torch.nn as nn
import torch.nn.functional as F
class CapsuleLayer(nn.Module):
def __init__(self, num_capsules, num_route_nodes, in_channels, out_channels):
super(CapsuleLayer, self).__init__()
self.num_route_nodes = num_route_nodes
self.num_capsules = num_capsules
self.capsules = nn.ModuleList([
nn.Conv2d(in_channels, out_channels, kernel_size=9, stride=2, padding=0)
for _ in range(num_capsules)
])
动态路由
接下来,我们需要实现胶囊间的动态路由算法。这通常包括一个或多个迭代过程,用于计算每个底层胶囊应该传递多少信息给每个上层胶囊。
def forward(self, x):
outputs = [capsule(x).view(x.size(0), -1, 1) for capsule in self.capsules]
outputs = torch.cat(outputs, dim=-1)
outputs = self.squash(outputs)
return outputs
def squash(self, tensor, dim=-1):
squared_norm = (tensor ** 2).sum(dim=dim, keepdim=True)
scale = squared_norm / (1 + squared_norm)
return scale * tensor / torch.sqrt(squared_norm)
构建完整模型
最后,我们将所有的胶囊层和其他标准网络层(如全连接层、损失层等)组合在一起,构建一个完整的胶囊网络模型。
class CapsuleNetwork(nn.Module):
def __init__(self):
super(CapsuleNetwork, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=256, kernel_size=9, stride=1)
self.primary_capsules = CapsuleLayer(num_capsules=8, num_route_nodes=-1, in_channels=256, out_channels=32)
self.digit_capsules = CapsuleLayer(num_capsules=10, num_route_nodes=32 * 6 * 6, in_channels=8, out_channels=16)
self.decoder = nn.Sequential(
nn.Linear(16 * 10, 512),
nn.ReLU(inplace=True),
nn.Linear(512, 1024),
nn.ReLU(inplace=True),
nn.Linear(1024, 784),
nn.Sigmoid()
)
5.2 训练
成功构建胶囊网络模型后,下一步是进行模型训练。训练过程中有几个关键因素需要特别注意,包括损失函数的选择、优化器的配置,以及评估指标的设计。
损失函数设计
胶囊网络的损失函数通常是一个组合损失,包括Reconstruction Loss(重建损失)和Margin Loss(边缘损失)。
class CapsuleLoss(nn.Module):
def forward(self, output, target, reconstructions, data):
# Margin loss
zero = torch.zeros(1)
margin_loss = target * torch.clamp(0.9 - output, min=0.) ** 2 \
+ 0.5 * (1. - target) * torch.clamp(output - 0.1, min=0.) ** 2
margin_loss = margin_loss.sum()
# Reconstruction loss
reconstruction_loss = F.mse_loss(reconstructions, data.view(reconstructions.size()[0], -1))
return (margin_loss + 0.0005 * reconstruction_loss)
优化器选择
通常使用Adam优化器,它的自适应学习速率通常在胶囊网络上表现得相对好。
from torch.optim import Adam
model = CapsuleNetwork()
optimizer = Adam(model.parameters())
训练循环
在训练循环内部,我们需要确保进行前向传播、计算损失、执行反向传播,并更新权重。
# 训练数据加载器
train_loader = ...
# 损失函数
criterion = CapsuleLoss()
for epoch in range(num_epochs):
model.train()
for batch_id, (data, target) in enumerate(train_loader):
optimizer.zero_grad()
output, reconstructions = model(data)
loss = criterion(output, target, reconstructions, data)
loss.backward()
optimizer.step()
模型评估
训练完成后,除了查看训练数据上的表现,还需要在验证数据集上进行评估。
model.eval()
total_correct = 0
total_test = 0
with torch.no_grad():
for batch_id, (data, target) in enumerate(test_loader):
output, _ = model(data)
pred = output.data.max(1)[1]
total_correct += pred.eq(target.data).cpu().sum()
total_test += len(data)
accuracy = total_correct / total_test
print(f'Test Accuracy: {accuracy}')
六、胶囊网络实际场景应用

胶囊网络作为深度学习的一个新兴领域,已经在多个实际应用场景中展现出其独特的优势。这些应用通常涉及到对几何变换具有高度敏感性或者需要高度精准表示层级结构的任务。
6.1 计算机视觉
对象识别
胶囊网络通过更精确地表示对象的各个部分和它们之间的空间关系,提供了比传统卷积神经网络更准确的对象识别。
图像分割
胶囊网络在语义分割任务中也表现出色,能够准确地将图像分割为多个不同的对象或区域。
6.2 医学图像分析
在医学影像如MRI和X光等的分析中,胶囊网络可以更准确地识别各种生物结构,从而有助于早期诊断和治疗方案制定。
6.3 自然语言处理
尽管自然语言处理(NLP)主要由循环神经网络和Transformer结构主导,胶囊网络也在一些特定任务中表现出其优势,如文本分类和情感分析。
6.4 强化学习
在复杂环境中,胶囊网络可以作为代理(Agent)的视觉模块,提供更精准的环境识别和理解,从而帮助代理更有效地作出决策。
七、总结
本文全面深入地探讨了胶囊网络(Capsule Networks)的原理、构建块、数学模型以及在PyTorch中的实现。我们还深入分析了胶囊网络在各种实际应用场景,如计算机视觉、医学图像分析等方面的性能和优势。通过本文,读者不仅能够理解胶囊网络的基础概念和高级数学原理,还能掌握其在实际问题中的应用方法。总体来说,胶囊网络作为深度学习的一个创新性发展,具有重要的理论和实用价值。
如有帮助,请多关注
TeahLead KrisChang,10+年的互联网和人工智能从业经验,10年+技术和业务团队管理经验,同济软件工程本科,复旦工程管理硕士,阿里云认证云服务资深架构师,上亿营收AI产品业务负责人。