HanLP — 感知机(Perceptron)
感知机(Perceptron)是一个二类分类的线性分类模型,属于监督式学习算法。
最终目的:
将不同的样本分类
感知机饮食了多个权重参数,输入的特征向量先是和对应的权重相乘,再加得到的积相加,然后将加权后的特征值送入激活函数,最后得到输出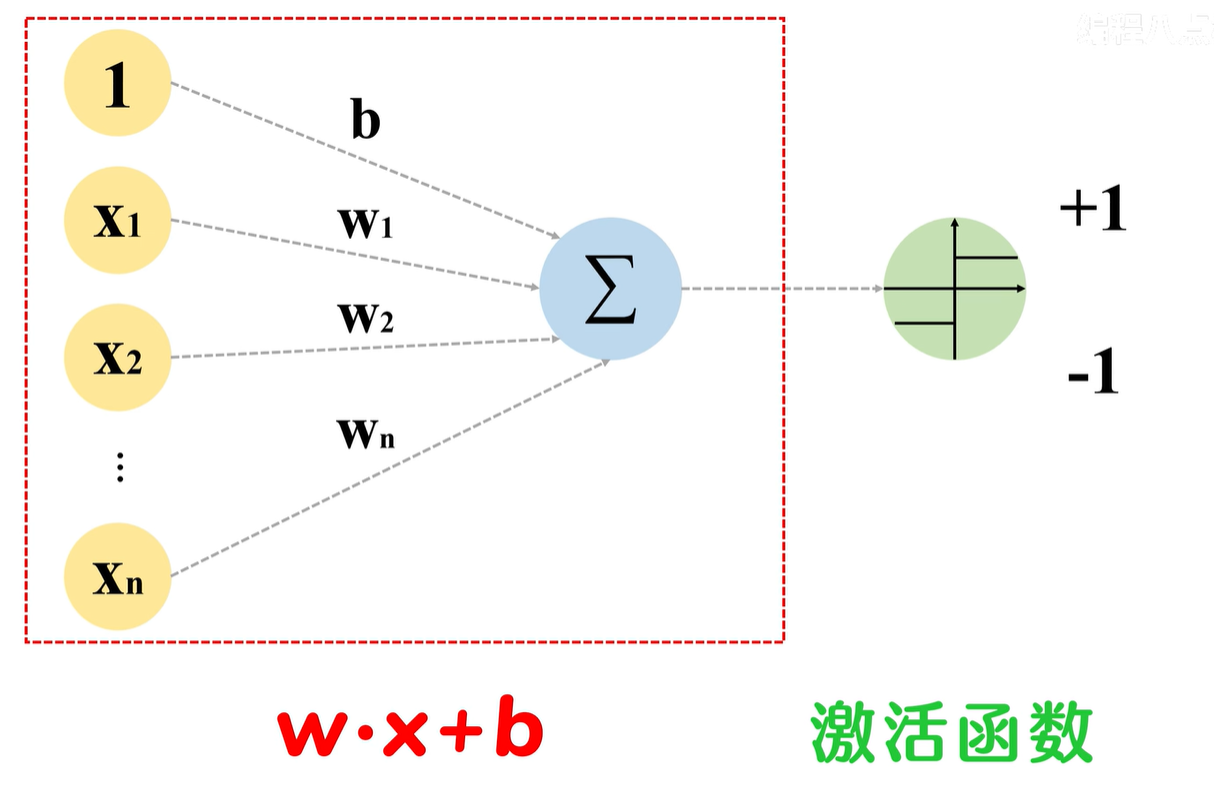
激活函数的前面部分,是线性方程
wx+b
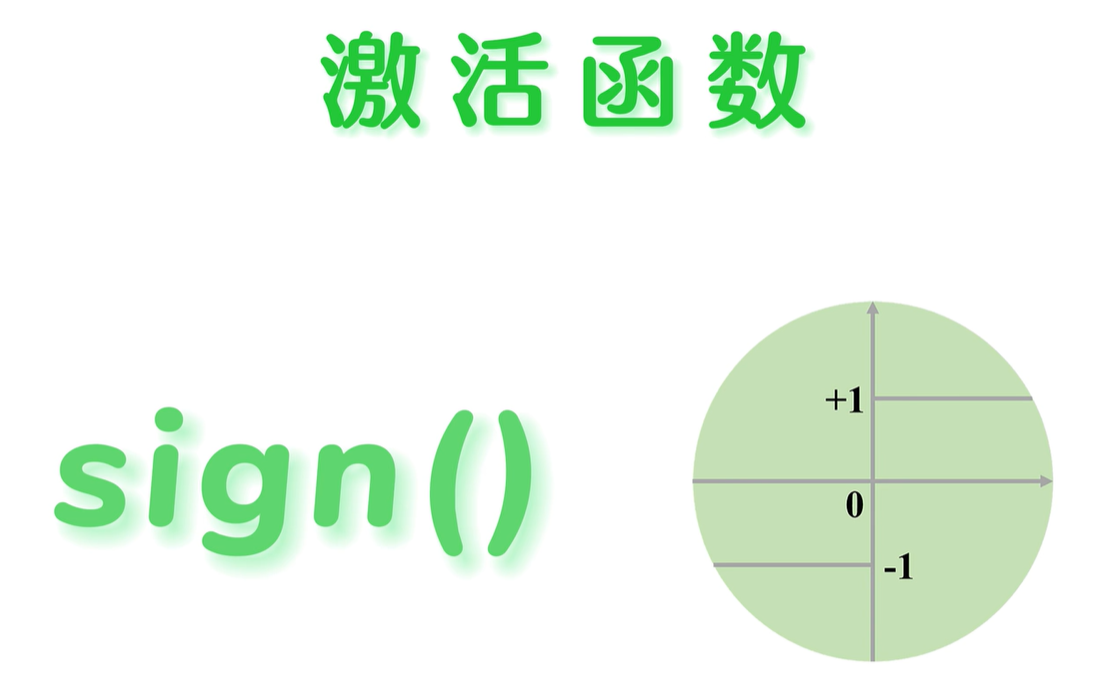
线性方程输出的是连续的值,但对于分类来说,最终需要的类别信息是离散的值,这时候,激活函数就派上用场了,激活函数的存在,是将连续回归值,转变成1 -1 这样的离散值,从而实现类别划分
激活函数
激活函数有很多种,在深度学习中,有着非常重要的作用,在感知机中使用的激活函数是
sin()
,
假如输入到模型中的是一个二维的特征向量(x1,x2),则整个过程可以表示为如下: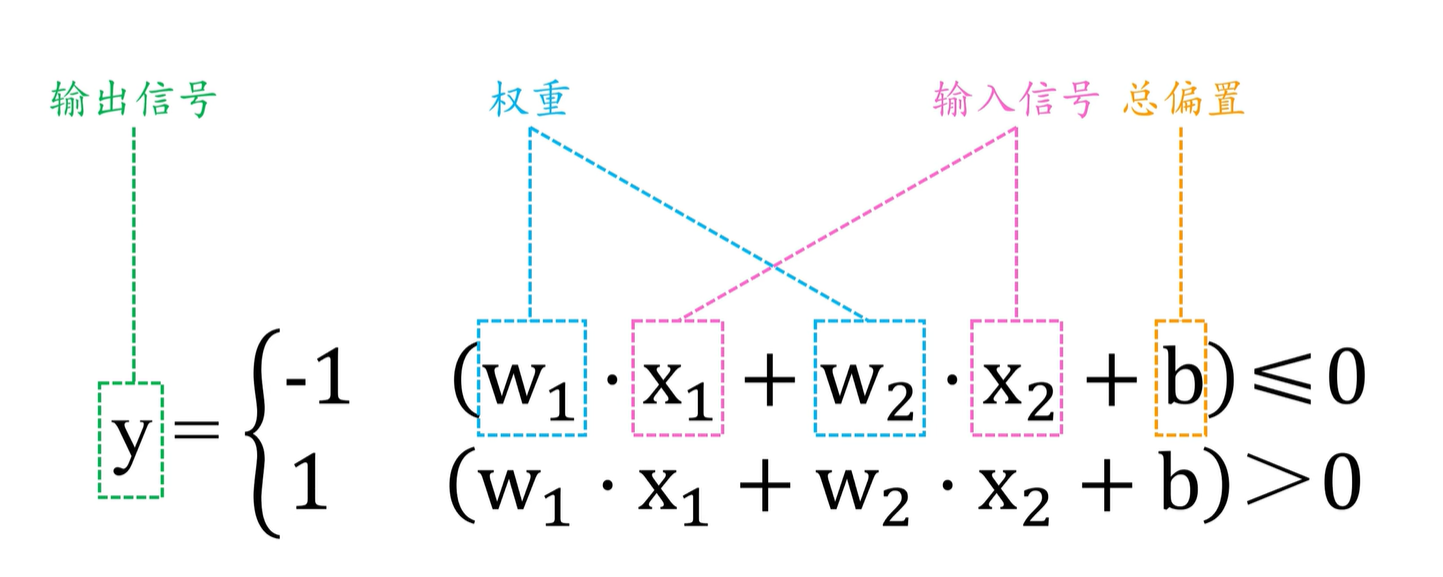
输入的特征向量(x1,x2)先分别和权重(w1,w2)相乘,再将两者相加,最后加上偏置 b ,最终得到的值,和阈值 0 做比较,如果值大于0 则输出1,否则则输出 -1
这样一来,就会划分到了线性方程 wx+b=0 两侧的样本,就分成了正、负两类,用感知机进行二分类,需要先找到能够将正、负样本完全区分开的决策函数
wx+b=0
,如下图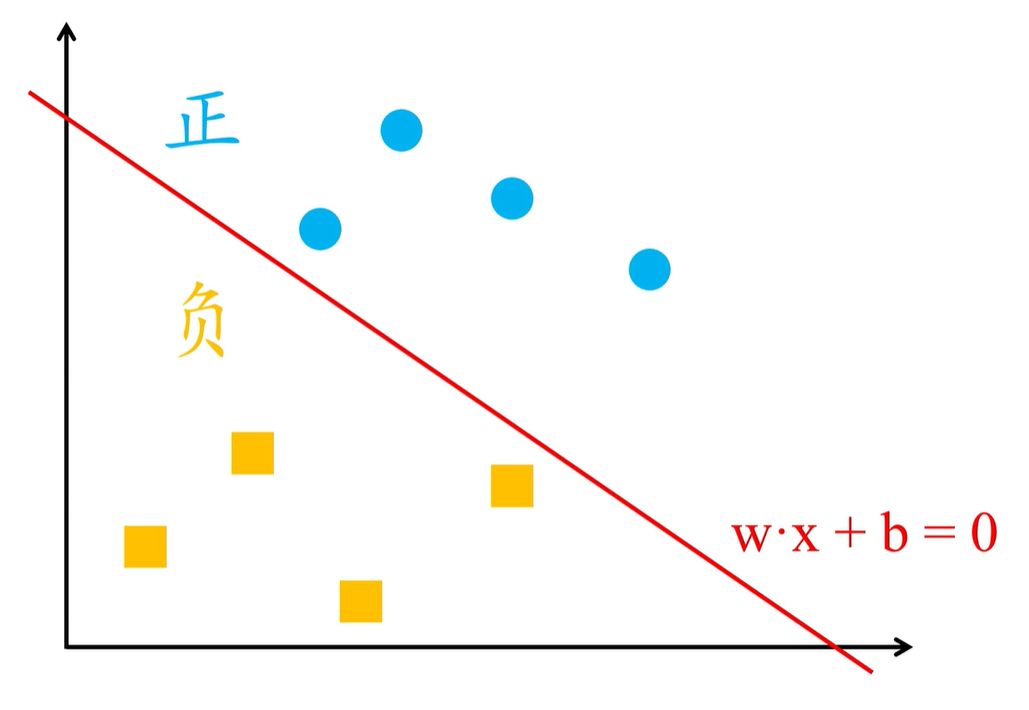
因此就需要确定一个学习策略,也就是定义一个
损失函数
,再通过训练样本,通过减小损失值,不断迭代模型参数,最终找到最优参数 w 和 b ,
损失函数的作用:
用来衡量模型的输出结果,和真实结果之间的偏差,然后根据偏差,修正模型,
回归任务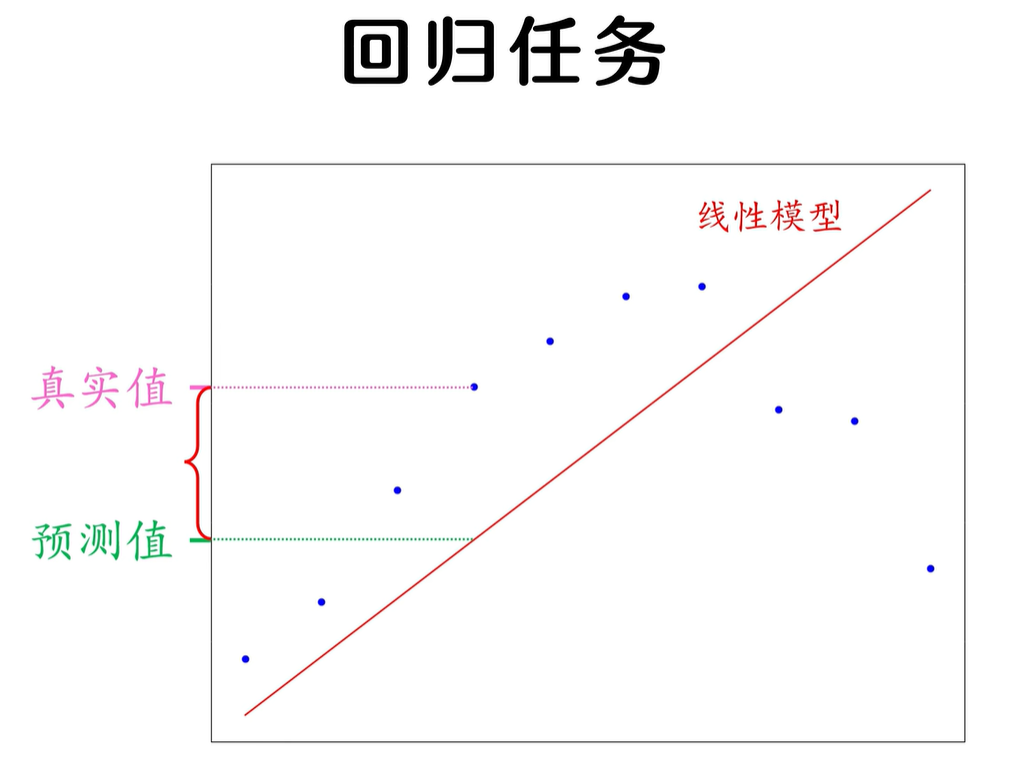
在回归任务中,标签和模型输出都是连续的数值,很容易就能衡量出二者之间的差异。
可对于感知机的分类问题来说,我们又该如何衡量差异呢?一个直观的想法,就是去统计误分类样本的个数作为损失值,误分类的样本个数越多,说明这个该样本空间下的表现越差,但是这样的函数是非连续的,对 w 和 b 不可导,所以我们无法使用这样的损失函数来更新 w 和 b.
为了得到连续可导的损失函数,感知机选择用误分类样本到决策函数的距离,来衡量偏差
这里是单个样本点到决策函数的距离公式
\(\frac {1}{||w||} |w*x_0+b|\)
其中
\(x_0\)
表示样本点的输入
\(||w||\)
等于权重向量
\(w\)
的模长
\(||w|| = \sqrt{(w_1^2 + w_2^2 + ... + w_n^2)}\)
对于感知机分类问题来说,可以用
\(-y_0(w*x_0+b)\)
来代替
\(|w*x_0+b|\)
\(y_0\)
表示样本点
\(x_0\)
对应的标签值。
为什么可以这样代替呢?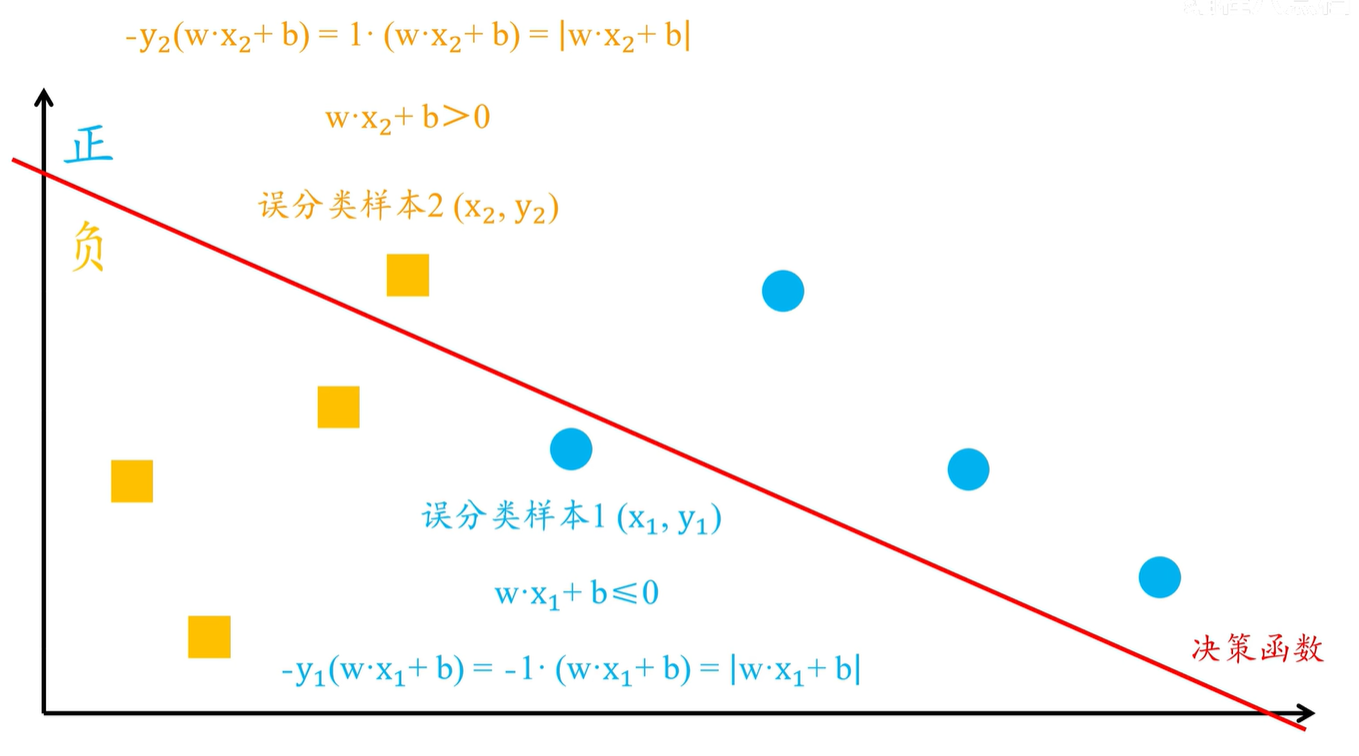
假设有两个误分类样本
样本1
\((x_1,y_1)\)
样本2 $(x_2,y_2)
\(,
样本1 的真实类别为正样本,即:\)
y_1 = 1$,但是在模型中,样本1 却被误分类为了负样本,也就是计算得到的
\(wx1+b \leq 0\)
,那么
\(-y_1(w*x_1+b)=-1(w*x_1+b)\)
最终的结果变成了正值,大小等于
\(|w*x_1+b|\)
样本2 的真实类别为负样本,
\(y_2=-1\)
即在模型中被误分类为了正样本。也就是计算得到的
\(w*x_2+b > 0\)
,那么
\(-y_2(w*x_2+b)\)
就等于
\(1(w*x_2+b)\)
,结果仍为正值,大小等于
\(|w*x_2+b|\)
因此:所有误分类的样本到决策函数的距离和就可以表示为如下
感知机所关心的,是怎么能将两类样本正确地区分开,对样本点到决策函数距离的大小并不关心,如下图,红线和绿线都能将两类样本正确地区分开,所以对感知机来说,这两条线的分类效果是一样的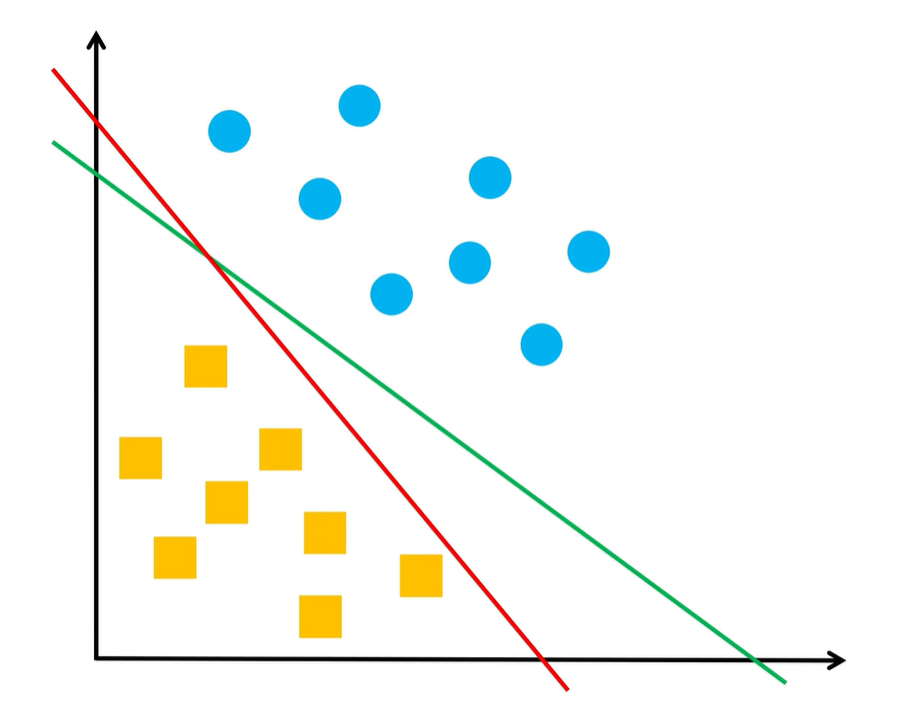
因此,可以把
\(\frac {1}{||w||}\)
去掉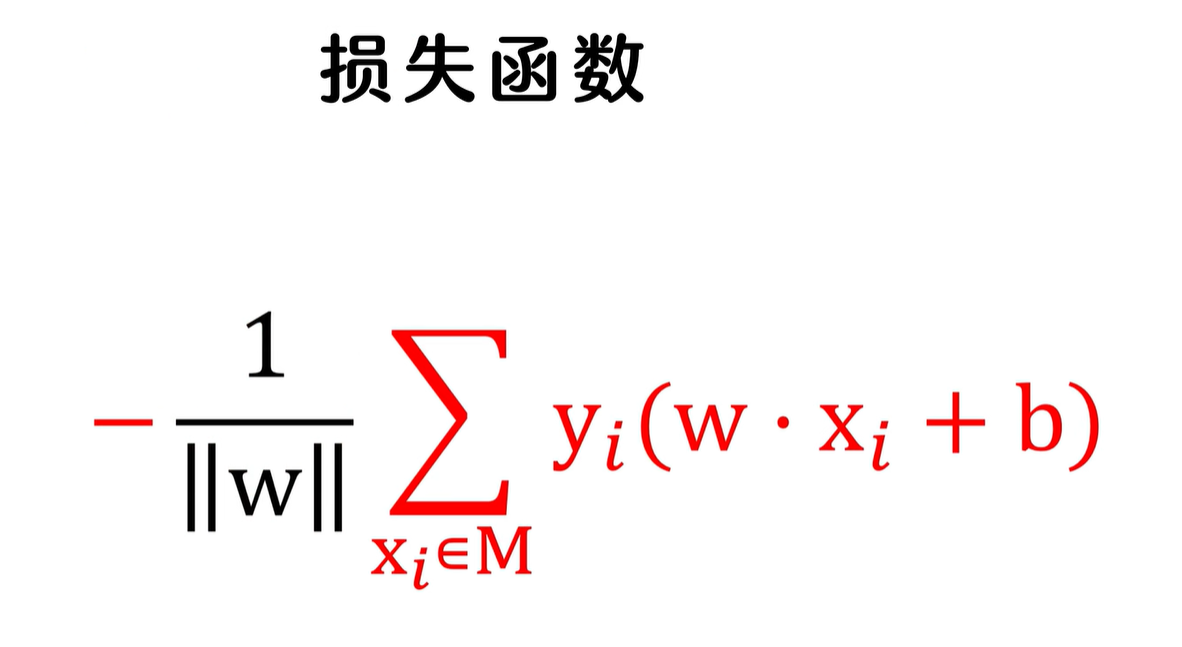
最终,感知机的函数就是 $$ L(w,b) = - \sum_{x_i{\in}M}y_i(w*x_i+b) $$
感知机适用于样本特征简单,且线性可分的二分类问题,因为运算简单,所以计算效率高。
不过在复杂的场景中,感知机往往不能胜任,所以我们在感知机的基础上,又诞生了多层感知机和神经网络