Softmax 回归

有一种
logistic
回归的一般形式，叫做
Softmax
回归，能让在试图识别某一分类时做出预测，或者说是多种分类中的一个，不只是识别两个分类，来一起看一下。

假设不单需要识别猫，而是想识别猫，狗和小鸡，把猫加做类1，狗为类2，小鸡是类3，如果不属于以上任何一类，就分到“其它”或者说“以上均不符合”这一类，把它叫做类0。这里显示的图片及其对应的分类就是一个例子，这幅图片上是一只小鸡，所以是类3，猫是类1，狗是类2，猜这是一只考拉，所以以上均不符合，那就是类0，下一个类3，以此类推。将会用符号表示，会用大写的
\(C\)
来表示的输入会被分入的类别总个数，在这个例子中，有4种可能的类别，包括“其它”或“以上均不符合”这一类。当有4个分类时，指示类别的数字，就是从0到
\(C-1\)
，换句话说就是0、1、2、3。

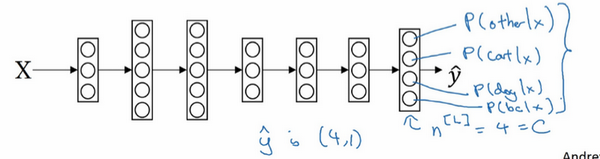
在这个例子中，将建立一个神经网络，其输出层有4个，或者说
\(C\)
个输出单元，因此
\(n\)
，即输出层也就是
\(L\)
层的单元数量，等于4，或者一般而言等于
\(C\)
。想要输出层单元的数字告诉这4种类型中每个的概率有多大，所以这里的第一个节点(最后输出的第1个方格+圆圈)输出的应该是或者说希望它输出“其它”类的概率。在输入
\(X\)
的情况下，这个(最后输出的第2个方格+圆圈)会输出猫的概率。在输入
\(X\)
的情况下，这个会输出狗的概率(最后输出的第3个方格+圆圈)。在输入
\(X\)
的情况下，输出小鸡的概率（最后输出的第4个方格+圆圈），把小鸡缩写为
bc
（
baby chick
）。因此这里的
\(\hat y\)
将是一个
\(4×1\)
维向量，因为它必须输出四个数字，给这四种概率，因为它们加起来应该等于1，输出中的四个数字加起来应该等于1。

让的网络做到这一点的标准模型要用到
Softmax
层，以及输出层来生成输出，让把式子写下来，然后回过头来，就会对
Softmax
的作用有一点感觉了。

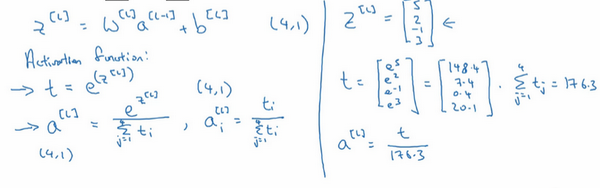
在神经网络的最后一层，将会像往常一样计算各层的线性部分，
\(z^{[l]}\)
这是最后一层的
\(z\)
变量，记住这是大写
\(L\)
层，和往常一样，计算方法是
\(z^{[l]} = W^{[l]}a^{[L-1]} + b^{[l]}\)
，算出了
\(z\)
之后，需要应用
Softmax
激活函数，这个激活函数对于
Softmax
层而言有些不同，它的作用是这样的。首先，要计算一个临时变量，把它叫做t，它等于
\(e^{z^{[l]}}\)
，这适用于每个元素，而这里的
\(z^{[l]}\)
，在的例子中，
\(z^{[l]}\)
是4×1的，四维向量
\(t=e^{z^{[l]}}\)
，这是对所有元素求幂，
\(t\)
也是一个4×1维向量，然后输出的
\(a^{[l]}\)
，基本上就是向量
\(t\)
，但是会归一化，使和为1。因此
\(a^{[l]} = \frac{e^{z^{[l]}}}{\sum_{j =1}^{4}t_{i}}\)
，换句话说，
\(a^{[l]}\)
也是一个4×1维向量，而这个四维向量的第
\(i\)
个元素，把它写下来，
\(a_{i}^{[l]} = \frac{t_{i}}{\sum_{j =1}^{4}t_{i}}\)
，以防这里的计算不够清晰易懂，马上会举个例子来详细解释。

来看一个例子，详细解释，假设算出了
\(z^{[l]}\)
，
\(z^{[l]}\)
是一个四维向量，假设为
\(z^{[l]} = \begin{bmatrix} 5 \\ 2 \\ - 1 \\ 3 \\ \end{bmatrix}\)
，要做的就是用这个元素取幂方法来计算
\(t\)
，所以
\(t =\begin{bmatrix} e^{5} \\ e^{2} \\ e^{- 1} \\ e^{3} \\ \end{bmatrix}\)
，如果按一下计算器就会得到以下值
\(t = \begin{bmatrix} 148.4 \\ 7.4 \\ 0.4 \\ 20.1 \\ \end{bmatrix}\)
，从向量
\(t\)
得到向量
\(a^{[l]}\)
就只需要将这些项目归一化，使总和为1。如果把
\(t\)
的元素都加起来，把这四个数字加起来，得到176.3，最终
\(a^{[l]} = \frac{t} {176.3}\)
。

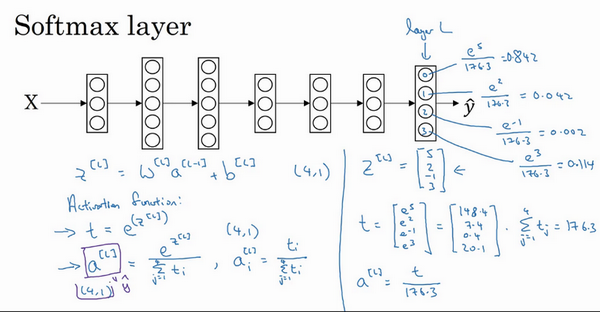
例如这里的第一个节点，它会输出
\(\frac{e^{5}}{176.3} =0.842\)
，这样说来，对于这张图片，如果这是得到的
\(z\)
值(
\(\begin{bmatrix} 5 \\ 2 \\ - 1 \\ 3 \\ \end{bmatrix}\)
)，它是类0的概率就是84.2%。下一个节点输出
\(\frac{e^{2}}{176.3} =0.042\)
，也就是4.2%的几率。下一个是
\(\frac{e^{- 1}}{176.3} =0.002\)
。最后一个是
\(\frac{e^{3}}{176.3} =0.114\)
，也就是11.4%的概率属于类3，也就是小鸡组，对吧？这就是它属于类0，类1，类2，类3的可能性。

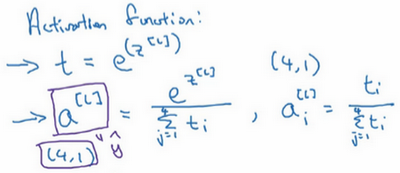
神经网络的输出
\(a^{[l]}\)
，也就是
\(\hat y\)
，是一个4×1维向量，这个4×1向量的元素就是算出来的这四个数字(
\(\begin{bmatrix} 0.842 \\ 0.042 \\ 0.002 \\ 0.114 \\ \end{bmatrix}\)
)，所以这种算法通过向量
\(z^{[l]}\)
计算出总和为1的四个概率。

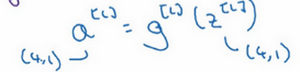
如果总结一下从
\(z^{[l]}\)
到
\(a^{[l]}\)
的计算步骤，整个计算过程，从计算幂到得出临时变量
\(t\)
，再归一化，可以将此概括为一个
Softmax
激活函数。设
\(a^{[l]} = g^{[l]}(z^{[l]})\)
，这一激活函数的与众不同之处在于，这个激活函数
\(g\)
需要输入一个4×1维向量，然后输出一个4×1维向量。之前，的激活函数都是接受单行数值输入，例如
Sigmoid
和
ReLu
激活函数，输入一个实数，输出一个实数。
Softmax
激活函数的特殊之处在于，因为需要将所有可能的输出归一化，就需要输入一个向量，最后输出一个向量。

那么
Softmax
分类器还可以代表其它的什么东西么？来举几个例子，有两个输入
\(x_{1}\)
，
\(x_{2}\)
，它们直接输入到
Softmax
层，它有三四个或者更多的输出节点，输出
\(\hat y\)
，将向展示一个没有隐藏层的神经网络，它所做的就是计算
\(z^{[1]} = W^{[1]}x + b^{[1]}\)
，而输出的出
\(a^{[l]}\)
，或者说
\(\hat y\)
，
\(a^{[l]} = y = g(z^{[1]})\)
，就是
\(z^{[1]}\)
的
Softmax
激活函数，这个没有隐藏层的神经网络应该能让对
Softmax
函数能够代表的东西有所了解。

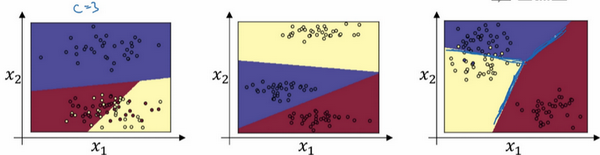
这个例子中（左边图），原始输入只有
\(x_{1}\)
和
\(x_{2}\)
，一个
\(C=3\)
个输出分类的
Softmax
层能够代表这种类型的决策边界，请注意这是几条线性决策边界，但这使得它能够将数据分到3个类别中，在这张图表中，所做的是选择这张图中显示的训练集，用数据的3种输出标签来训练
Softmax
分类器，图中的颜色显示了
Softmax
分类器的输出的阈值，输入的着色是基于三种输出中概率最高的那种。因此可以看到这是
logistic
回归的一般形式，有类似线性的决策边界，但有超过两个分类，分类不只有0和1，而是可以是0，1或2。

这是（中间图）另一个
Softmax
分类器可以代表的决策边界的例子，用有三个分类的数据集来训练，这里（右边图）还有一个。对吧，但是直觉告诉，任何两个分类之间的决策边界都是线性的，这就是为什么看到，比如这里黄色和红色分类之间的决策边界是线性边界，紫色和红色之间的也是线性边界，紫色和黄色之间的也是线性决策边界，但它能用这些不同的线性函数来把空间分成三类。

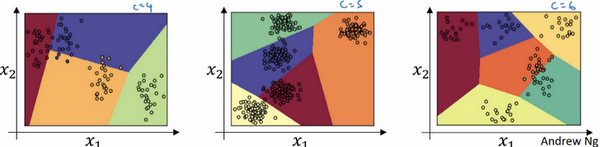
来看一下更多分类的例子，这个例子中（左边图）
\(C=4\)
，因此这个绿色分类和
Softmax
仍旧可以代表多种分类之间的这些类型的线性决策边界。另一个例子（中间图）是
\(C=5\)
类，最后一个例子（右边图）是
\(C=6\)
，这显示了
Softmax
分类器在没有隐藏层的情况下能够做到的事情，当然更深的神经网络会有
\(x\)
，然后是一些隐藏单元，以及更多隐藏单元等等，就可以学习更复杂的非线性决策边界，来区分多种不同分类。