[数据结构] 树、森林及二叉树的应用
树、森林
树的存储结构
双亲表示法
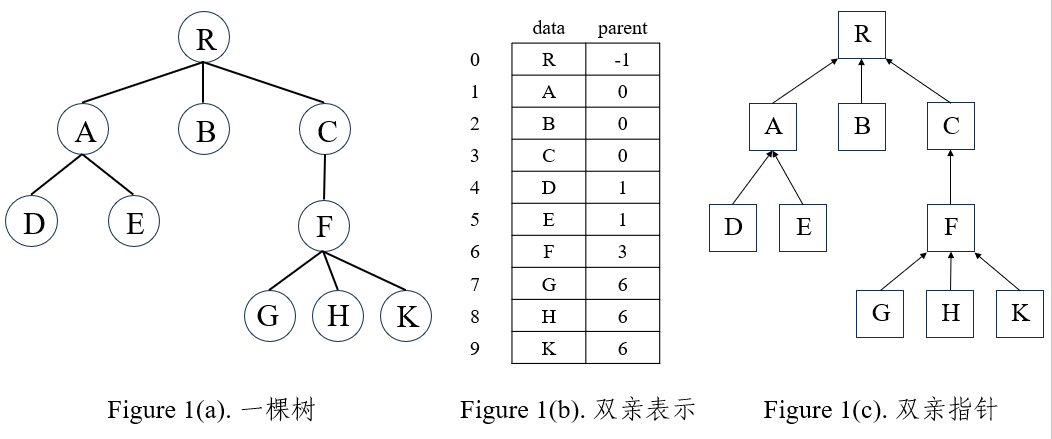
双亲表示法的存储结构
#define MAX_TREE_SIZE 100
typedef struct {
int data;
int parent;
}PTNode;
typedef struct {
PTNode nodes[MAX_TREE_SIZE];
int n;
}PTree;
【注】
区别树的顺序存储结构与二叉树的顺序存储结构。在树的顺序存储结构中,数组下标代表节点的编号,下标中所存的内容指示了节点之间的关系。而在二叉树的顺序存储结构中, 数组下标既表达了节点的编号,又指示了二叉树中节点之间的关系。当然,二叉树属于树,因此二叉树也可以用树的存储结构来存储,但树却不能都用都用二叉树的存储结构来存储。
孩子表示法
孩子表示法是将每个节点的孩子节点视为一个线性表,且以单链表作为存储结构,则
\(n\)
个节点就有
\(n\)
个孩子链表(叶节点的孩子链表为空表)。而
\(n\)
个头指针又组成一个线性表。
与双亲表示法相反,孩子表示法寻找孩子的操作非常方便,而寻找双亲的操作则需要遍历
\(n\)
个节点中孩子链表指针域所指向的
\(n\)
个孩子链表。
孩子兄弟表示法
又称
二叉树表示法
,即以二叉链表作为树的存储结构。孩子兄弟表示法使每个节点包括三个部分的内容:
节点值、指向节点第一个孩子节点的指针、指向节点下一个兄弟节点的指针
结构体如下:
typedef struct CSNode {
inr data;
struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;
树、森林、二叉树的转换
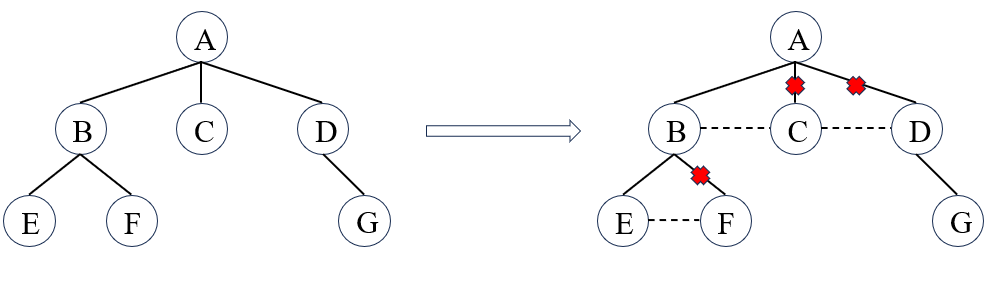
树转换为二叉树
(1)在兄弟节点之间画一条线;
(2)对每个节点,只保留它与第一个孩子的连线,而与其他孩子的连线全部删除;
(3)以树根为轴心,顺时针旋转45°。
以下代码引用我大佬同学:作者:Amαdeus,出处:https://www.cnblogs.com/MAKISE004/p/17089756.html //树 转化为 二叉树 BinaryTree CSTree_Transform_to_BinaryTree(CSTree ct){ if(!ct) return NULL; BinaryTree T = (BinaryTree)malloc(sizeof(BiNode)); T->data = ct->data; //相当于将left变为firstchild, 将right变为nextsibling 本质的形态没有改变 T->leftchild = CSTree_Transform_to_BinaryTree(ct->firstchild); T->rightchild = CSTree_Transform_to_BinaryTree(ct->nextsibling); return T; }
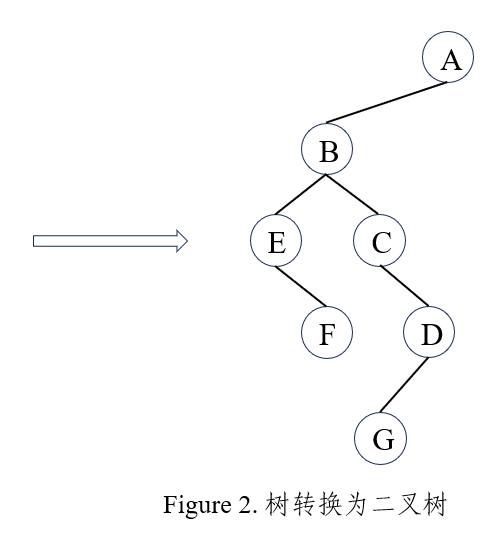
森林转换为二叉树
(1)将森林中的每棵树转换成相应的二叉树;
(2)每棵树的根视为兄弟关系,加上连线;
(3)以第一棵树的根为轴心顺时针旋转45°。
以下代码引用我大佬同学:作者:Amαdeus,出处:https://www.cnblogs.com/MAKISE004/p/17089756.html //森林 转化为 二叉树 BinaryTree Forest_Transform_to_BinaryTree(CSTree ct[], int low, int high){ if(low > high) return NULL; //每个树变成二叉树 BinaryTree T = CSTree_Transform_to_BinaryTree(ct[low]); //通过rightchild连接每一个二叉树的根节点 T->rightchild = Forest_Transform_to_BinaryTree(ct, low + 1, high); return T; }
树、森林的遍历
树的遍历
先根遍历。若树非空,则按如下规则遍历:
- 先访问根节点
- 再依次遍历根节点的每棵子树,遍历子树时仍遵循先根后子树的规则
后根遍历。若树非空,则按如下规则遍历:
- 先依次遍历根节点的每棵子树,遍历子树时仍遵循先子树后根的规则
- 再访问根节点
树的先根遍历与对应二叉树的先序序列相同,树的后根遍历与对应二叉树的中序序列相同。
森林的遍历
先序遍历森林。若森林非空,则按如下规则遍历:
- 访问森林中第一棵树的根节点
- 先序遍历第一棵树中根节点的子树森林
- 先序遍历除去第一棵树之后剩余的树构成的森林
中序遍历森林。若森林非空,则按如下规则遍历:
- 中序遍历森林中第一棵树的根节点的子树森林
- 访问第一棵树的根节点
- 中序遍历粗去第一棵树之后剩余的树构成的森林
树与二叉树的应用
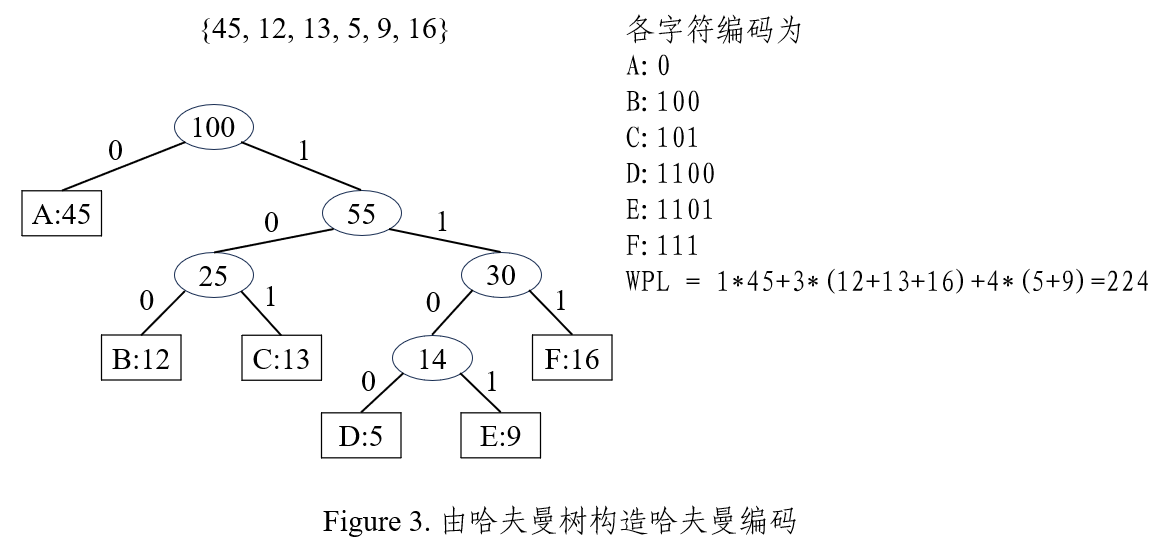
哈夫曼树和哈夫曼编码
几个概念
路径:树中一个节点到另一个节点之间的分支构成
路径长度:路径上的分支数目
权:树中节点被赋予的一个表示某种意义的数值
带权路径长度:从树的根到一个节点的路径长度与该节点上权值的乘积
\[WPL = \sum_{i=1}^{n}w_il_i
\]
其中,
\(w_i\)
是第
\(i\)
个叶节点所带的权值,
\(l_i\)
是该叶节点到根节点的路径长度
在含有
\(n\)
个带权叶节的二叉树中,其中带权路径长度最小的二叉树称为
哈夫曼树
。
下面看个算法:递归求WPL
int getWPL(struct TreeNode *root, int depth) {
if (root == NULL) { // 如果节点为空,返回0
return 0;
}
if (root->left == NULL && root->right == NULL) { // 如果节点是叶子节点,返回带权路径长度
return depth * root->val;
}
// 如果节点不是叶子节点,递归计算左子树和右子树的WPL,并相加返回
return getWPL(root->left, depth + 1) + getWPL(root->right, depth + 1);
}
接下来咱们举个栗子,来看一下哈夫曼编码
看题:来自北邮考研机试
题解:
// 优先队列求哈夫曼树最短带权路径长度
#include<bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
priority_queue<int, vector<int>, greater<int> > q;
for(int i = 0; i < n; i ++) {
int x;
cin >> x;
q.push(x);
}
int ans = 0;
while(q.size() > 1) {
int t1 = q.top();
q.pop();
int t2 = q.top();
q.pop();
q.push(t1 + t2);
ans += t1 + t2;
}
cout << ans << endl;
return 0;
}
并查集
这里不想做太多解释,我们看一下y总的模版(写的时候已经快要零点了,第二天还要早起)
(PS:第二天果然多睡了半个小时)
(1)朴素并查集:
int p[N]; //存储每个点的祖宗节点
// 返回x的祖宗节点
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
(2)维护size的并查集:
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) {
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合:
size[find(b)] += size[find(a)];
p[find(a)] = find(b);
(3)维护到祖宗节点距离的并查集:
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离
// 返回x的祖宗节点
int find(int x) {
if (p[x] != x) {
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) {
p[i] = i;
d[i] = 0;
}
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量
作者:yxc
链接:https://www.acwing.com/blog/content/404/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int p[N];//定义多个集合
int find(int x) {
if(p[x] != x) p[x] = find(p[x]);
/*
经上述可以发现,每个集合中只有祖宗节点的p[x]值等于他自己,即:
p[x]=x;
*/
return p[x];
//找到了便返回祖宗节点的值
}C
int main() {
int n, m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++) p[i]=i;
while(m --) {
char op[2];
int a, b;
scanf("%s%d%d", op, &a, &b);
if(*op == 'M') p[find(a)] = find(b);//集合合并操作
else
if(find(a)==find(b))
//如果祖宗节点一样,就输出yes
printf("Yes\n");
else
printf("No\n");
}
return 0;
}