决策树的生成

有了信息增益和信息增益比，我就可以以此衡量特征的相对好坏，进而可以用于决策树的生成。相对应的基于信息增益计算的方法所生成的决策树的算法我们叫做ID3算法，而基于信息增益的算法我们叫做C4.5，二者唯一的区别就在于一个使用信息增益衡量特征好坏而另外一个使用信息增益比，因此本文重点讲述ID3算法。

ID3算法

1. 特殊情况判断
   
   • 如果数据集中所有的样本均属于同一类
     \(C_k\)
     ，那么直接将
     \(C_k\)
     作为该结点的类别标记，并返回决策树
     \(T\)
     。
   • 如果此时特征集合
     \(A=\varnothing\)
     为空，那么将
     \(D\)
     中相同类别数最多样本的类别作为该结点的类别标记并返回
     \(T\)
     。
2. 若没有出现上述特殊情况，则计算
   \(A\)
   中各特征的信息增益
   \(g(D, A_i)\)
   ，并选择信息增益最大的特征
   \(A_g\)
   。
3. 若
   \(A_g\)
   的信息增益小于阈值
   \(\epsilon\)
   ，那么同样的，将
   \(D\)
   中相同类别数最多的样本的类别作为该结点的类别标记并返回
   \(T\)
   。
4. 否则使用
   \(A_g=a_i\)
   再次将训练集分割为若干非空子集
   \(D_i\)
   ，其中
   \(a_i\)
   是特征
   \(A_g\)
   的每个可能取值，然后对每一个
   \(D_i\)
   以其实例数最大的类作为标记构建子节点。
5. 对第
   \(i\)
   个子结点以
   \(D_i\)
   为训练集，特征集合
   \(A=A - {A_g}\)
   为特征集，递归调用
   \((1)-(5)\)
   。

下面是更形象化的图示：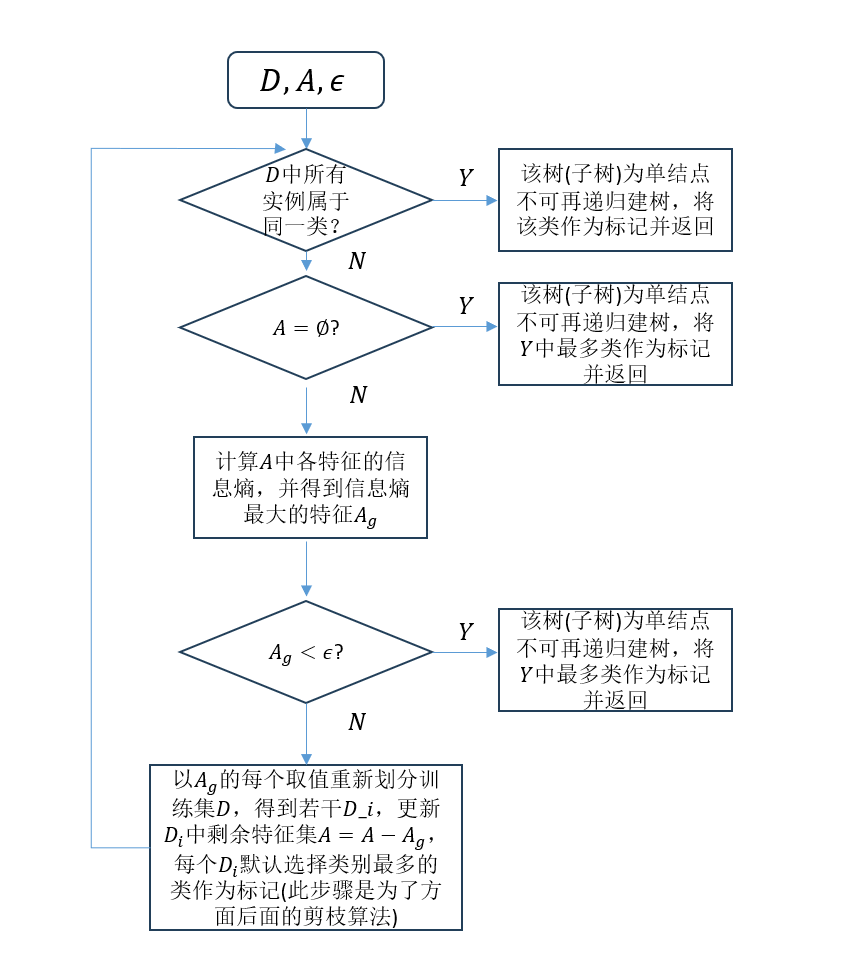

决策树的剪枝

为了减少决策树的复杂度，并降低过拟合，对决策树进行剪枝是十分有必要的。

代价复杂度剪枝

设决策树
\(T\)
的叶子结点个数为
\(|T|\)
，叶子结点表示为
\(t\)
，
\(N_t\)
表示
\(t\)
上的所有样本点，
\(N_{tk}\)
表示第
\(k\)
类的样本点，
\(H_t(T)\)
表示叶子节点
\(t\)
上的经验熵(损失)。

那么决策树的损失函数可以定义为

前一项表示模型对训练数据的预测误差。

算法

对每个叶子节点的父节点进行剪枝，设剪枝前树的损失为
\(T_\alpha(T_A)\)
，为剪枝的为
\(T_\alpha(T_B)\)
，若满足

则表明需要进行剪枝，此过程持续进行，直到无法再继续剪枝。