浮点数(小数)在计算机中如何用二进制存储？

【版权声明】未经博主同意，谢绝转载！（请尊重原创，博主保留追究权）
https://www.cnblogs.com/cnb-yuchen/p/18107586
出自【
进步*于辰的博客
】

注：为了阐述更加严谨，本篇文章中将使用一些二进制的相关概念，出自上篇博文。

前言

在解析
Float类
的源码时，我对
MAX_VALUE/MIN_VALUE
的值很好奇，它们是怎么来的？于是利用我所知的二进制知识，尝试运算。一开工就发现没辙，因为我压根不知道小数的二进制是怎样表示、又是如何存储的。于是寻得一方案：

启发博文：
浮点数(小数)在计算机中如何用二进制存储？
（转发）。

这位博主的阐述专业且详细，下面我通过个人理解，尽量简明扼要地为大家阐明这个知识点。

正文

在开始之前，大家先看一张图。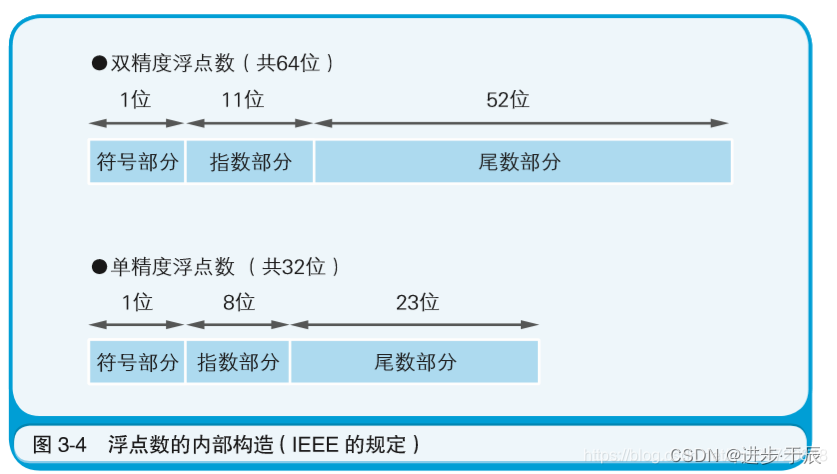

Float 就是单精度，就是说 Float 变量由
32
位（4字节）二进制表示。现在大家对这张图有所疑惑，无妨，我要表达的意思是，小数的二进制由三部分组成，与整数完全不同。换言之，给我们一组小数的二进制，我们无法直接看出它的
真值
是多少。因此，需要使用一种纸面上的二进制数表现形式。

如何运算出这种纸面上的二进制数表现形式？
所谓纸面上，就是一目了然，也就是使用整数二进制的表现形式去表现小数。那位博主是这样说的：

二进制转换为十进制的方法就是各个位的数字与位权乘积之和。

什么是“位权”？这张图给了答案。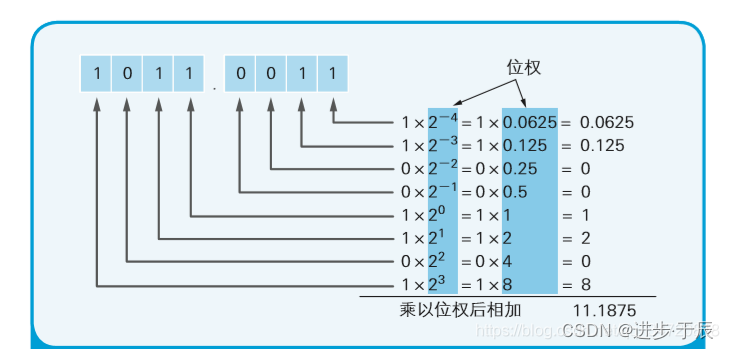

就是
底数的指数幂
。

答案很清楚了，可是如何运算浮点数的小数部分的二进制，难道使用如上“求和”的方法？当然可以，不过不太方便。

从另一位博主那儿“取经”得一方法：使用上图示例。整数部分照旧，是
1011
，将小数部分
0.1875
进行以下运算：

0.1875 * 2 = 0.3750 → 0
0.3750 * 2 = 0.7500 → 0
0.7500 * 2 = 1.5000 → 1
0.5000 * 2 = 1.0000 → 1

得
0011
。

结论：

将小数部分乘以
2
，取结果的整数部分，如此反复，直至结果为
0
，最后依次得到的整数部分就是小数部分的二进制。

PS：暂不懂其中原理，就挺好用。

补充一点
：那位博主将
100
个 float 类型的
0.1
相加，最终结果不是
10.0
。

大家便可明了，无论二选一，
0.1
都是无限小数。无论单双精度，都无法表示完全，必然有所缺失或增加（四舍五入），故是
10.000002
。

成功了一半，可
1011.0011
只是
11.1875
在纸面上的二进制数表现形式。

浮点数(小数)在计算机中如何用二进制存储？
回到第一张图，小数的二进制由符号、指数、尾数三部分组成，这说明必然有一个公式，将这三部分进行运算，从而得到“真值”。

公式是这样的：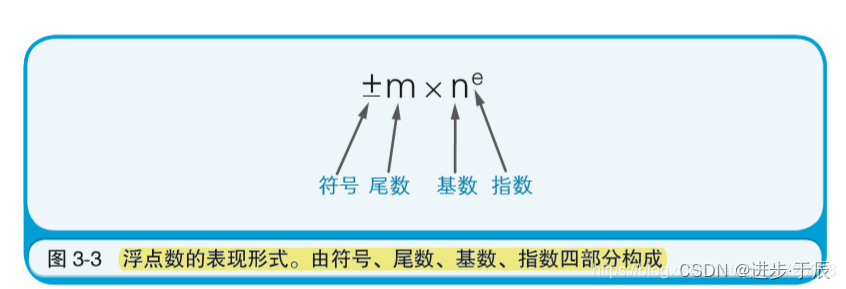

二进制中基数（又称“底数”）是
2
，自然不必考虑。小数内部构造的三部分正好与图中三个未知变量对应，下面我一一剖析。（以单精度为例）

符号部分占
1
位，即
0/1
。（PS：小数没有“补码”之说）

指数部分（
8
位）与尾数部分（
23
位）又是如何表示小数的？

我们来探讨一下，看到
m * n
^e
这样的公式，给你
11.1875
这个小数，你能想到哪些等式？

11.1875 = 666666.875 * 10
^-1
，m是
666666.875
，n是
10
，e是
-1
11.1875 = 1.11875 * 10
¹
， m是
1.11875
，n是
10
，e是
1
......

有问题么？这里是二进制，n 是
2
，不是
10
，故等式不能这么写。

可是要满足如下等式，m 是多少？

11.1875 = m * 2
^-1
11.1875 = m * 2
¹
......

看到这样的等式，大家是否似曾相识？没错，位运算，也就是这样：

11.1875 = m * 2
^-1
= m >> 1
11.1875 = m * 2
¹
= m << 1
......

明白了么？

可这里有个问题，因为位运算移动的位数
e
是任意的，故
m
任意，则必然存在一个规范，用于限制
e
的值。

规范定义：

尾数部分用的是“将小数点前面的值固定为
1
的正则表达式”。
什么是正则表达式？按照特定的规则来表示数据的形式的表达式。

这样就清楚了，规范就是“
将小数点左边第一位固定为
1
，其他为
0
”。如此，
e
就只有一个值。

PS：不过，对于那位博主将规范定义为“正则表达式”这一点，我的个人看法是，意思没错，可用词似乎不恰当，当时我就被误导了。当然，也可能是我的功底不扎实。

规范知道了，可尾数
m
是多少呢？大家在上文的阅读中有没有注意到一个细节？就是“
纸面上的二进制数表现形式
”那儿，我最后说了一句：“成功了一半”。成功在哪？又何出此言？

其实，
小数在纸面上的二进制数表现形式就是
m * 2
^e
的结果
。以
11.1875
为例：

11.1875 → 1011.0011

规范是“将小数点左边第一位固定为
1
，其他为
0
”，就是这样：

11.1875
→
1011.0011
=
1.0110011
<< 3 =
1.0110011
* 2
³

这样，难道 m 是
1.0110011
？当然不是，那位博主已阐明：

因此，m 是
01100110000000000000000
。e 是
3
。

对应到小数的内部构造，
11.1875
的二进制是：

0 00000011 01100110000000000000000

这是正确答案吗？还不是。

运用以上方法，我们来计算一下
0.1875
的二进制：

0.0011						原始数值
1.1							左移使个位为 1
1.10000000000000000000000	确保小数点后有23位
10000000000000000000000		仅保留小数点后的部分

得出，m 是
10000000000000000000000
，e 是
-3
。

因此，
0.1875
的二进制是
0 10000011 10000000000000000000000
。（指数
e
使用的是“原码”，不是“补码”）

这样看来，似乎没有问题，可实际上指数部分还有点“门道”。

那位博主阐述道：

指数部分使用了“
EXCESS系统表现
”。

什么是“EXCESS系统表现”？那位博主已阐述得很清楚，我就不赘述了。

总结：

• 11.1875
  的二进制是
  0 10000010 01100110000000000000000
  。
• 0.1875
  的二进制是
  0 06666661100 10000000000000000000000
  。

PS：

1. 如果采用双精度，同理，只是二进制位数增加了而已。
2. 那位博主运用 c++ 代码进行了验证，我把他提供的 code copy test 了一下，同样验证无误，只是目前我暂不知如何使用 java 进行验证，需要大家自行研究了。

本文完结。

上一篇：《
二进制相关概念、运算与应用
》。