OI-Wiki 学习笔记
算法基础
\(\text{Update: 2024 - 07 - 22}\)
复杂度
定义
衡量一个算法的快慢,一定要考虑数据规模的大小。
一般来说,数据规模越大,算法的用时就越长。
而在算法竞赛中,我们衡量一个算法的效率时,最重要的不是看它在某个数据规模下的用时,而是看它的用时随数据规模而增长的趋势,即
时间复杂度
。
符号定义
相等是
\(\Theta\)
,小于是
\(O\)
,大于是
\(\Omega\)
。
大
\(\Theta\)
符号
对于函数
\(f(n)\)
和
\(g(n)\)
,
\(f(n)=\Theta(g(n))\)
,当且仅当
\(\exists c_1,c_2,n_0>0\)
,使得
\(\forall n \ge n_0, 0\le c_1\cdot g(n)\le f(n) \le c_2\cdot g(n)\)
。
大
\(O\)
符号
\(\Theta\)
符号同时给了我们一个函数的上下界,如果只知道一个函数的渐进上界而不知道其渐进下界,可以使用
\(O\)
符号。
\(f(n) = O(g(n))\)
,当且仅当
\(\exists c,n_0\)
,使得
\(\forall n \ge n_0,0\le f(n)\le c\cdot g(n)\)
。
研究时间复杂度时通常会使用
\(O\)
符号,因为我们关注的通常是程序用时的上界,而不关心其用时的下界。
大
\(\Omega\)
符号
同样的,我们使用
\(\Omega\)
符号来描述一个函数的渐进下界。
\(f(n) = \Omega(g(n))\)
,当且仅当
\(\exists c, n_0\)
,使得
\(\forall n \ge n_0, 0 \le c \cdot g(n) \le f(n)\)
。
主定理
建议背下来,不是很好理解。
\]
那么
\]
需要注意的是,这里的第二种情况还需要满足
\(\text{regularity condition}\)
, 即
\(a f(n/b) \leq c f(n)\)
,
\(\text{for some constant}\)
\(c < 1\)
\(\text{and sufficiently large}\)
\(n\)
。
几个例子:
\(T(n) = 2T(\frac{n}{2}) + 1\)
,那么
\(a = 2, b = 2, {\log_2 2} = 1\)
,那么
\(\epsilon\)
可以取值在
\((0, 1]\)
之间,从而满足第一种情况,所以
\(T(n) = \Theta(n)\)
。\(T(n) = T(\frac{n}{2}) + n\)
,那么
\(a = 1, b = 2, {\log_2 1} = 0\)
,那么
\(\epsilon\)
可以取值在
\((0, 1]\)
之间,从而满足第二种情况,所以
\(T(n) = \Theta(n)\)
。\(T(n) = T(\frac{n}{2}) + {\log n}\)
,那么
\(a = 1, b = 2, {\log_2 1} = 0\)
,那么
\(k\)
可以取值为
\(1\)
,从而满足第三种情况,所以
\(T(n) = \Theta(\log^2 n)\)
。\(T(n) = T(\frac{n}{2}) + 1\)
,那么
\(a = 1, b = 2, {\log_2 1} = 0\)
,那么
\(k\)
可以取值为
\(0\)
,从而满足第三种情况,所以
\(T(n) = \Theta(\log n)\)
。
空间复杂度
类似地,算法所使用的空间随输入规模变化的趋势可以用
空间复杂度
来衡量。
枚举
实际上一些题的正解就是枚举,但需要很多优化。
要点:
建立简洁的数学模型。
减少不必要的枚举空间。
选择合适的枚举顺序。
模拟
模拟即为将题目描述中的操作用代码实现,码量一般比较大,写错比较难调,相当浪费时间。
写模拟题时有以下注意的点:
在写代码之前,尽量在演草纸上自习分析题目的实现过程。
在代码中尽量把每个部分抽离出来写成函数,模块化。
将题目中的信息转化,不要残留多种表达。
如果一次没过大样例,分块调试。
实现代码时按照演草纸上的思路一步步实现。
递归
定义
我们可以用以下代码理解递归:
long long f(传入数值) {
if(终止条件) return 最小子问题解;
return f(缩小问题规模);
}
递归的优点
- 结构清晰、可读性强,可以参考归并排序的两种实现方式。
- 练习分析为题的结构,当发现问题可以分解成相同结构的小问题时,递归写多了就能敏锐发现这个特点,进而高效解决问题。
递归的缺点
在程序执行中,递归是利用堆栈来实现的。每当进入一个函数调用,栈就会增加一层栈帧,每次函数返回,栈就会减少一层栈帧。而栈不是无限大的,当递归层数过多时,就会造成
栈溢出
的后果。
显然有时候递归处理是高效的,比如归并排序;
有时候是低效的
,比如数孙悟空身上的毛,因为堆栈会消耗额外空间,而简单的递推不会消耗空间。比如这个例子,给一个链表头,计算它的长度:
// 典型的递推遍历框架
int size(Node *head) {
int size = 0;
for (Node *p = head; p != nullptr; p = p->next) size++;
return size;
}
// 我就是要写递归,递归天下第一
int size_recursion(Node *head) {
if (head == nullptr) return 0;
return size_recursion(head->next) + 1;
}
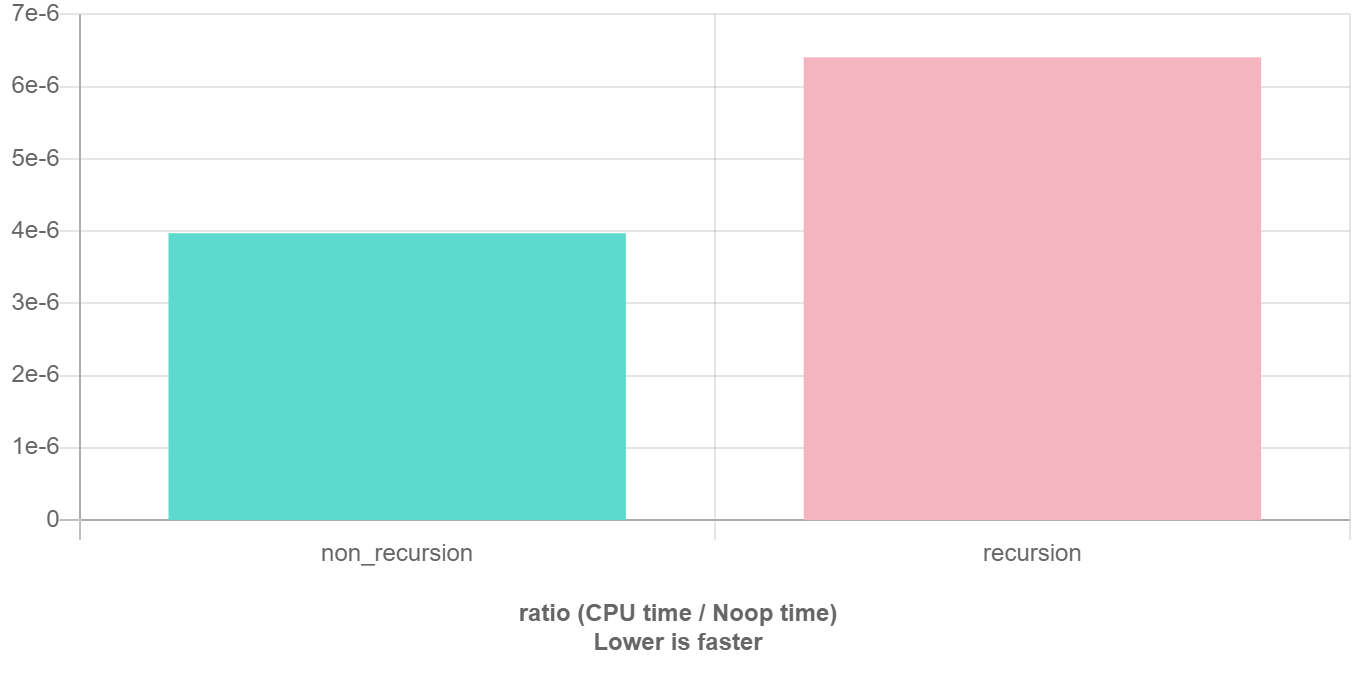
递归优化见后文
搜索优化
和
记忆化搜索
。
要点
明白一个函数的作用并相信它能完成这个任务,千万不要跳进这个函数里面企图探究更多细节,否则就会陷入无穷的细节无法自拔,人脑能压几个栈啊。
递归与枚举的区别
枚举是横向地把问题划分,然后依次求解子问题;而递归是把问题逐级分解,是纵向的拆分。
递归与分治的区别
递归是一种编程技巧,一种解决问题的思维方式;分治算法很大程度上是基于递归的,解决更具体问题的算法思想。
分治
定义
就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
过程
分治算法的核心思想就是「分而治之」。
大概的流程可以分为三步:分解
\(\to\)
解决
\(\to\)
合并。
分解原问题为结构相同的子问题。
分解到某个容易求解的边界之后,进行递归求解。
将子问题的解合并成原问题的解。
分治法能解决的问题一般有如下特征:
该问题的规模缩小到一定的程度就可以容易地解决。
该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质,利用该问题分解出的子问题的解可以合并为该问题的解。
该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
注意:如果各子问题是不独立的,则分治法要重复地解公共的子问题,也就做了许多不必要的工作。此时虽然也可用分治法,但一般用动态规划较好。
贪心
适用范围
贪心算法在有最优子结构的问题中尤为有效。
最优子结构的意思是问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
证明
贪心算法有两种证明方法:反证法和归纳法。
一般情况下,一道题只会用到其中的一种方法来证明。
反证法:如果交换方案中任意两个元素/相邻的两个元素后,答案不会变得更好,那么可以推定目前的解已经是最优解了。
归纳法:先算得出边界情况(例如
\(n = 1\)
)的最优解
\(F_1\)
,然后再证明:对于每个
\(n\)
,
\(F_{n + 1}\)
都可以由
\(F_{n}\)
推导出结果。
常见题型
在提高组难度以下的题目中,最常见的贪心有两种。
「我们将
\(XXX\)
按照某某顺序排序,然后按某种顺序(例如从小到大)选择。」。「我们每次都取
\(XXX\)
中最大/小的东西,并更新
\(XXX\)
。」(有时「
\(XXX\)
中最大/小的东西」可以优化,比如用优先队列维护)
二者的区别在于一种是离线的,先处理后选择;一种是在线的,边处理边选择。
排序解法
用排序法常见的情况是输入一个包含几个(一般一到两个)权值的数组,通过排序然后遍历模拟计算的方法求出最优值。
后悔解法
思路是无论当前的选项是否最优都接受,然后进行比较,如果选择之后不是最优了,则反悔,舍弃掉这个选项;否则,正式接受。如此往复。
排序
几种排序算法的比较
一张表格速通
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 空间 | 稳定性 |
|---|---|---|---|---|---|
| 选择排序 | \(O(n^2)\) | \(O(n^2)\) | \(O(n^2)\) | \(O(1)\) | 不稳定 |
| 冒泡排序 | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) | \(O(1)\) | 稳定 |
| 插入排序 | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) | \(O(n)\) | 稳定 |
| 计数排序 | \(O(n + w)^1\) | \(O(n + w)\) | \(O(n + w)\) | \(O(n + w)\) | 稳定 |
| 基数排序 | \(O(kn + \sum\limits_{i = 1}^{k} w_i)^2\) | \(O(kn + \sum\limits_{i = 1}^{k} w_i)\) | \(O(kn + \sum\limits_{i = 1}^{k} w_i)\) | \(O(n + k)\) | 稳定 |
| 快速排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n^2)\) | \(O(\log n) \sim O(n)\) | 不稳定 |
| 归并排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n)\) | 稳定 |
| 堆排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n \log n)\) | \(O(1)\) | 不稳定 |
| 桶排序 | \(O(n + \frac{n^2}{k} + k)^3\) | \(O(n)\) | \(O(n^2)\) | \(O(n + m)^4\) | 稳定 |
| 希尔排序 | \(O(n \log n) \sim O(n^2)\) | \(O(n^{1.3})\) | \(O(n^2)\) | \(O(1)\) | 不稳定 |
| 锦标赛排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n)\) | 稳定 |
| \(\text{tim}\) 排序 |
\(O(n \log n)\) | \(O(n)\) | \(O(n \log n)\) | \(O(n)\) | 稳定 |
\(^1\)
:其中
\(w\)
为排序元素的值域。
\(^2\)
:其中
\(k\)
为排序元素的最大位数,
\(w_i\)
为第
\(i\)
个关键字的值域。
\(^3\)
:其中
\(k\)
表示将
\(n\)
个元素放进
\(m\)
个桶中,每个桶的数据为
\(k = \frac{n}{m}\)
。
\(^4\)
:其中
\(m\)
表示将
\(n\)
个元素放进的
\(m\)
个桶。
前缀和
定义
前缀和可以简单理解为「数列的前
\(\text{i}\)
项的和」,是一种重要的预处理方式,能大大降低查询的时间复杂度。
一维前缀和
预处理递推式为:
\]
查询
\([l, r]\)
的数值:
\]
二维前缀和
预处理递推式为:
\]
查询
\((i, j) \sim (k, w)\)
的数值:
\]
树上前缀和
设
\(s_i\)
表示结点
\(i\)
到根节点的权值总和。
若是点权,
\(x, y\)
路径上的和为
\(s_x + s_y - s_{lca} - s_{fa_{lca}}\)
若是边权,
\(x, y\)
路径上的和为
\(s_x + s_y - 2 \times s_{lca}\)
差分
定义
差分是一种和前缀和相对的策略,可以当作是求和的逆运算。
这种策略的定义是令
\(b_i = \begin{cases} a_i - a_{i - 1} \, &i \in[2, n] \\ a_1 \, &i = 1 \end{cases}\)
性质
\(a_i\)
的值是
\(b_i\)
的前缀和,即
\(a_n = \sum\limits_{i = 1}^n b_i\)
。计算
\(a_i\)
的前缀和
\(sum = \sum\limits_{i = 1}^n a_i = \sum\limits_{i = 1}^n \sum\limits_{j = 1}^{i} b_j = \sum\limits_{i = 1}^n (n - i + 1) b_i\)
。
它可以维护多次对序列的一个区间加上一个数,并在最后询问某一位的数或是多次询问某一位的数。注意修改操作一定要在查询操作之前。
树上差分
树上差分可以理解为对树上的某一段路径进行差分操作,这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作,并且询问某条边或者某个点在经过操作后的值的时候,就可以运用树上差分思想了。
树上差分通常会结合树基础和最近公共祖先来进行考察。树上差分又分为
点差分
与
边差分
,在实现上会稍有不同。
点差分
举例:对树上的一些路径
\(\delta(s_1, t_1), \delta(s_2, t_2), \delta(s_3, t_3)\dots\)
进行访问,问一条路径
\(\delta(s, t)\)
上的点被访问的次数。
对于一次
\(\delta(s, t)\)
的访问,需要找到
\(s\)
与
\(t\)
的公共祖先,然后对这条路径上的点进行访问(点的权值加一),若采用
\(\text{DFS}\)
算法对每个点进行访问,由于有太多的路径需要访问,时间上承受不了。这里进行差分操作:
&d_s\leftarrow d_s + 1\\
&d_{lca}\leftarrow d_{\textit{lca}} - 1\\
&d_t\leftarrow d_t + 1\\
&d_{f(\textit{lca})}\leftarrow d_{f(\textit{lca})} - 1\\
\end{aligned}
\]
其中
\(f(x)\)
表示
\(x\)
的父亲节点,
\(d_i\)
为点权
\(a_i\)
的差分数组。
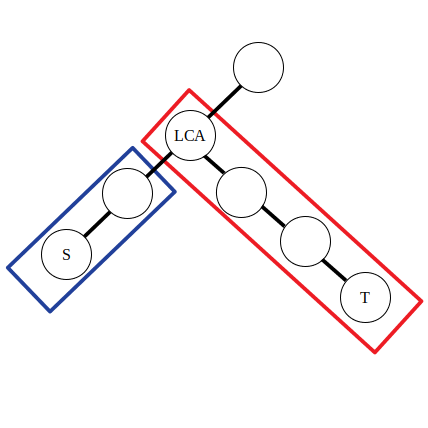
可以认为公式中的前两条是对蓝色方框内的路径进行操作,后两条是对红色方框内的路径进行操作。不妨令
\(\textit{lca}\)
左侧的直系子节点为
\(\textit{left}\)
。那么有
\(d_{\textit{lca}} - 1 = a_{\textit{lca}} - (a_{\textit{left}} + 1)\)
,
\(d_{f(\textit{lca})} - 1 = a_{f(\textit{lca})} - (a_{\textit{lca}} + 1)\)
。可以发现实际上点差分的操作和上文一维数组的差分操作是类似的。
边差分
若是对路径中的边进行访问,就需要采用边差分策略了,使用以下公式:
&d_s\leftarrow d_s + 1\\
&d_t\leftarrow d_t + 1\\
&d_{\textit{lca}}\leftarrow d_{\textit{lca}} - 2\\
\end{aligned}
\]
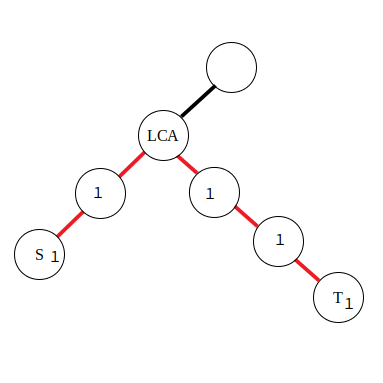
由于在边上直接进行差分比较困难,所以将本来应当累加到红色边上的值向下移动到附近的点里,那么操作起来也就方便了。对于公式,有了点差分的理解基础后也不难推导,同样是对两段区间进行差分。
\(\text{Update: 2024 - 07 - 23}\)
二分
时间复杂度
二分查找的最优时间复杂度为
\(O(1)\)
,平均时间复杂度和最坏时间复杂度均为
\(O(\log n)\)
。
空间复杂度
迭代版本的二分查找的空间复杂度为
\(O(1)\)
。
递归(无尾调用消除)版本的二分查找的空间复杂度为
\(O(\log n)\)
。
三分法
三分法衍生自二分法,三分法求单峰函数的峰值。
算法流程:
设当前搜索域为
\([l,r]\)
,取该区间的三等分点
\(\text{lmid,rmid}\)
。
若满足
\(f(\text{lmid})<f(\text{rmid})\)
,则可以排除
\([l,\text{lmid}]\)
。
若满足
\(f(\text{lmid})=f(\text{rmid})\)
,则可以排除
\([l,\text{lmid}] \cup [\text{rmid},r]\)
。
若满足
\(f(\text{lmid})>f(\text{rmid})\)
,则可以排除
\([\text{rmid},r]\)
。
实数三分
double l = L, r = R;
for(int i = 1; i <= 100; i ++) {
double lmid = l + (r - l) / 3, rmid = r - (r - l) / 3;
if(f(lmid) < f(rmid)) l = lmid;
else r = rmid;
}
double ans = f(l);
整数三分
long long l = L, r = R;
while(r - l > 3) {
long long lmid = l + (r - l) / 3, rmid = r - (r - l) / 3;
if(f(lmid) < f(rmid)) l = lmid;
else r = rmid;
}
long long ans = f(l);
for(int i = l + 1; i <= r; i ++) ans = max(ans, f(i));
算法优化:
考虑计算时间复杂度,由于每次搜索域缩减到
\(\frac{2}{3}\)
。
因此时间复杂度为
\(O(\log_{\frac{3}{2}} \frac{R - L}{eps})\)
。
我们完全可以将
\(\text{lmid}\)
和
\(\text{rmid}\)
不断接近,以此达到使
\(\log\)
的底数无限接近
\(2\)
。
在单峰性/单谷性能够证明的题目中,三分法都能高效地适配。
分数规划
分数规划通常描述为下列问题:每个物品有两个属性
\(c_i, d_i\)
,要求通过某种方式选出若干个,使得
\(\frac{\sum c_i}{\sum d_i}\)
最大或最小。
经典的例子有最优比率环、最优比率生成树等等。
分数规划可以用二分法来解决。
倍增
倍增在很多算法中均有运用,其中最常用的是
\(\text{RMQ}\)
问题和求
\(\text{LCA}\)
。
构造
构造题是比赛中常见的一类题型。
从形式上来看,问题的答案往往具有某种规律性,使得在问题规模迅速增大的时候,仍然有机会比较容易地得到答案。
这要求解题时要思考问题规模增长对答案的影响,这种影响是否可以推广。
例如,在设计动态规划方法的时候,要考虑从一个状态到后继状态的转移会造成什么影响。
特点
构造题一个很显著的特点就是高自由度,也就是说一道题的构造方式可能有很多种,但是会有一种较为简单的构造方式满足题意。
看起来是放宽了要求,让题目变的简单了,但很多时候,正是这种高自由度导致题目没有明确思路而无从下手。
构造题另一个特点就是形式灵活,变化多样。并不存在一个通用解法或套路可以解决所有构造题,甚至很难找出解题思路的共性。
例题
例一:
构造一组
\(x,y,z\)
,使得对于给定的
\(n\)
,满足
\(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \dfrac{2}{n}\)
解题思路:
显然
\(n, n + 1, n(n + 1)\)
为一组合法解。特殊地,当
\(n = 1\)
时,无解,这是因为
\(n + 1\)
与
\(n(n + 1)\)
此时相等。
至于构造思路是怎么产生的,大概就是观察样例加上一点点数感了吧。此题对于数学直觉较强的人来说并不难。
例二:
\(\text{Task1}\)
:试判断能否构造并构造一个长度为
\(n\)
的
\(1\dots n\)
的排列,满足其
\(n\)
个前缀和在模
\(n\)
的意义下互不相同
\(\text{Task2}\)
:试判断能否构造并构造一个长度为
\(n\)
的
\(1\dots n\)
的排列,满足其
\(n\)
个前缀积在模
\(n\)
的意义下互不相同
解题思路:
对于
\(\text{task1}\)
:
当
\(n\)
为奇数时,无法构造出合法解;
当
\(n\)
为偶数时,可以构造一个形如
\(n, 1, n - 2, 3, \cdots\)
这样的数列。
首先,我们可以发现
\(n\)
必定出现在数列的第一位,否则
\(n\)
出现前后的两个前缀和必然会陷入模意义下相等的尴尬境地;
然后,我们考虑构造出整个序列的方式:
考虑通过构造前缀和序列的方式来获得原数列,可以发现前缀和序列两两之间的差在模意义下不能相等,因为前缀和序列的差分序列对应着原来的排列。
因此我们尝试以前缀和数列在模意义下为
\]
这样的形式来构造这个序列,不难发现它完美地满足所有限制条件。
对于
\(\text{task2}\)
:
当
\(n\)
为除
\(4\)
以外的合数时,无法构造出合法解
当
\(n\)
为质数或
\(4\)
时,可以构造一个形如
\(1, \dfrac{2}{1}, \dfrac{3}{2}, \cdots, \dfrac{n - 1}{n - 2}, n\)
这样的数列
先考虑什么时候有解:
显然,当
\(n\)
为合数时无解。因为对于一个合数来说,存在两个比它小的数
\(p,q\)
使得
\(p \times q \equiv 0 \pmod n\)
,如
\((3 \times 6) \% 9 = 0\)
。那么,当
\(p, q\)
均出现过后,数列的前缀积将一直为
\(0\)
,故合数时无解。特殊地,我们可以发现
\(4 = 2 \times 2\)
,无满足条件的
\(p, q\)
,因此存在合法解。
我们考虑如何构造这个数列:
和
\(\text{task1}\)
同样的思路,我们发现
\(1\)
必定出现在数列的第一位,否则
\(1\)
出现前后的两个前缀积必然相等;而
\(n\)
必定出现在数列的最后一位,因为
\(n\)
出现位置后的所有前缀积在模意义下都为
\(0\)
。分析题目给出的几组样例以后发现,所有样例中均有一组合法解满足前缀积在模意义下为
\(1, 2, 3, \cdots, n\)
,因此我们可以构造出上文所述的数列来满足这个条件。那么我们只需证明这
\(n\)
个数互不相同即可。
我们发现这些数均为
\(1 \cdots n - 2\)
的逆元
\(+ 1\)
,因此各不相同,此题得解。
例三:
给定一个整数
\(N\)
,试构造一个节点数为
\(N\)
无向图。令节点编号为
\(1\ldots N\)
,要求其满足以下条件:
- 这是一个简单连通图。
- 存在一个整数
\(S\)
使得对于任意节点,与其相邻节点的下标和为
\(S\)
。
保证输入数据有解。
解题思路:
通过分析
\(n = 3, 4, 5\)
的情况,我们可以找到一个构造思路。
构造一个完全
\(k\)
分图,保证这
\(k\)
部分和相等。则每个点的
\(S\)
均相等,为
\(\dfrac{(k - 1)\sum_{i = 1}^{n}i}{k}\)
。
如果
\(n\)
为偶数,那么我们可以前后两两配对,即
\(\{1, n\}, \{2, n - 1\} \cdots\)
如果
\(n\)
为奇数,那么我们可以把
\(n\)
单拿出来作为一组,剩余的
\(n - 1\)
个两两配对,即
\(\{n\}, \{1, n - 1\}, \{2, n - 2\}\cdots\)
这样构造出的图在
\(n \ge 3\)
时连通性易证,在此不加赘述。
此题得解。
搜索
\(\text{Update: 2024 - 07 - 24}\)
简介
搜索,也就是对状态空间进行枚举,通过穷尽所有的可能来找到最优解,或者统计合法解的个数。
搜索有很多优化方式,如减小状态空间,更改搜索顺序,剪枝等。
搜索是一些高级算法的基础,在
\(\text{OI}\)
中,纯粹的搜索往往也是得到部分分的手段,但可以通过纯粹的搜索拿到满分的题目非常少。
习题
DFS
先举一个例子:
把正整数
\(n\)
分解为
\(3\)
个不同的正整数,如
\(6 = 1 + 2 + 3\)
,排在后面的数必须大于等于前面的数,输出所有方案。
这个问题很简单,直接三层循环暴力就能解决:
for(int i = 1; i <= n; i ++)
for(int j = i + 1; j <= n; j ++)
for(int k = j + 1; k <= n; k ++)
if(i + j + k == n) cout << n << " = " << i << " + " << j << " + " << k << "\n";
但如果是把正整数
\(n\)
分为
\(m\)
个不同的数,那么单纯的循环就解决不了了,总不能写
\(m\)
层循环吧。
这时就要用到递归搜索了即
\(\text{DFS}\)
。
该类搜索算法的特点在于,将要搜索的目标分成若干「层」,每层基于前几层的状态进行决策,直到达到目标状态。
考虑上述问题,即将正整数
\(n\)
分解成小于等于
\(m\)
个正整数之和,且排在后面的数必须大于等于前面的数,并输出所有方案。
设一组方案将正整数
\(n\)
分解成
\(k\)
个正整数
\(a_1, a_2, \ldots, a_k\)
的和。
我们将问题分层,第
\(i\)
层决定
\(a_i\)
。则为了进行第
\(i\)
层决策,我们需要记录三个状态变量:
\(n-\sum_{j=1}^i{a_j}\)
,表示后面所有正整数的和;以及
\(a_{i-1}\)
,表示前一层的正整数,以确保正整数递增;以及
\(i\)
,确保我们最多输出
\(m\)
个正整数。
为了记录方案,我们用 arr 数组,第 i 项表示
\(a_i\)
. 注意到 arr 实际上是一个长度为
\(i\)
的栈。
int m, arr[103]; // arr 用于记录方案
void dfs(int n, int i, int a) {
if(n == 0) {
for (int j = 1; j <= i - 1; ++j) printf("%d ", arr[j]);
printf("\n");
}
if(i <= m) {
for(int j = a; j <= n; ++j) {
arr[i] = j;
dfs(n - j, i + 1, j);
}
}
}
// 主函数
scanf("%d %d", &n, &m);
dfs(n, 1, 1);
BFS
\(\text{BFS}\)
是图论中的一种遍历算法,详见下文。
\(\text{BFS}\)
在搜索中也很常用,将每个状态对应为图中的一个点即可。
Meet in the middle
\(\text{Meet in the middle}\)
也称双向搜索。
算法的基本思路就是从状态图上的起点和终点同时开始
\(\text{DFS}\)
或
\(\text{BFS}\)
。
如果发现搜索的两端相遇了,那么可以认为是获得了可行解。
双向
\(\text{BFS}\)
的过程:
将开始结点和目标结点加入队列 q
标记开始结点为 1
标记目标结点为 2
while(队列 q 不为空) {
从 q.front() 扩展出新的 s 个结点
如果 新扩展出的结点已经被其他数字标记过
那么 表示搜索的两端碰撞
那么 循环结束
如果 新的 s 个结点是从开始结点扩展来的
那么 将这个 s 个结点标记为 1 并且入队 q
如果 新的 s 个结点是从目标结点扩展来的
那么 将这个 s 个结点标记为 2 并且入队 q
}
性质
暴力搜索的复杂度往往是指数级的,而改用
\(\text{Meet in the middle}\)
算法后复杂度的指数可以减半,即
\(O(a^b) \to O(a^{\frac{b}{2}})\)
。
启发式搜索
定义
启发式搜索(英文:
\(\text{heuristic search}\)
)是一种在普通搜索算法的基础上引入了启发式函数的搜索算法。
启发式函数的作用是基于已有的信息对搜索的每一个分支选择都做估价,进而选择分支。简单来说,启发式搜索就是对取和不取都做分析,从中选取更优解或删去无效解。
例题
题目大意:
有
\(N\)
种物品和一个容量为
\(W\)
的背包,每种物品有重量
\(w_i\)
和价值
\(v_i\)
两种属性,要求选若干个物品(每种物品只能选一次)放入背包,使背包中物品的总价值最大,且背包中物品的总重量不超过背包的容量。
解题思路:
我们写一个估价函数
\(f\)
,可以剪掉所有无效的
\(0\)
枝条(就是剪去大量无用不选枝条)。
估价函数
\(f\)
的运行过程如下:
我们在取的时候判断一下是不是超过了规定体积(可行性剪枝);在不取的时候判断一下不取这个时,剩下的药所有的价值 + 现有的价值是否大于目前找到的最优解(最优性剪枝)。
示例代码:
#include <algorithm>
#include <cstdio>
using namespace std;
const int N = 105;
int n, m, ans;
struct Node {
int a, b; // a 代表时间,b 代表价值
double f;
} node[N];
bool operator<(Node p, Node q) { return p.f > q.f; }
int f(int t, int v) { // 计算在当前时间下,剩余物品的最大价值
int tot = 0;
for (int i = 1; t + i <= n; i++)
if (v >= node[t + i].a) {
v -= node[t + i].a;
tot += node[t + i].b;
} else
return (int)(tot + v * node[t + i].f);
return tot;
}
void work(int t, int p, int v) {
ans = max(ans, v);
if (t > n) return; // 边界条件:只有 n 种物品
if (f(t, p) + v > ans) work(t + 1, p, v); // 最优性剪枝
if (node[t].a <= p) work(t + 1, p - node[t].a, v + node[t].b); // 可行性剪枝
}
int main() {
scanf("%d %d", &m, &n);
for (int i = 1; i <= n; i++) {
scanf("%d %d", &node[i].a, &node[i].b);
node[i].f = 1.0 * node[i].b / node[i].a; // f 为性价比
}
sort(node + 1, node + n + 1); // 根据性价比排序
work(1, m, 0);
printf("%d\n", ans);
return 0;
}
A*
定义
\(A^*\)
搜索算法(英文:
\(A^* \text{search algorithm}\)
,
\(A^*\)
读作
\(\text{A-star}\)
),简称
\(A^*\)
算法,是一种在图形平面上,对于有多个节点的路径求出最低通过成本的算法。它属于图遍历(英文:
\(\text{Graph traversal}\)
)和最佳优先搜索算法(英文:
\(\text{Best-first search}\)
),亦是
\(\text{BFS}\)
的改进。
过程
定义起点
\(s\)
,终点
\(t\)
,从起点(初始状态)开始的距离函数
\(g(x)\)
,到终点(最终状态)的距离函数
\(h(x)\)
,
\(h^{\ast}(x)^1\)
,以及每个点的估价函数
\(f(x) = g(x) + h(x)\)
。
\(A^*\)
算法每次从优先队列中取出一个
\(f\)
最小的元素,然后更新相邻的状态。
如果
\(h\leq h*\)
,则
\(A^*\)
算法能找到最优解。
上述条件下,如果
\(h\)
满足三角形不等式,则
\(A^*\)
算法不会将重复结点加入队列。
当
\(h=0\)
时,
\(A^*\)
算法变为
\(\text{Dijkstra}\)
;当
\(h=0\)
并且边权为
\(1\)
时变为
\(\text{BFS}\)
。
例题
八数码
。
题目大意:
在
\(3\times 3\)
的棋盘上,摆有八个棋子,每个棋子上标有
\(1\)
至
\(8\)
的某一数字。棋盘中留有一个空格,空格用
\(0\)
来表示。空格周围的棋子可以移到空格中,这样原来的位置就会变成空格。给出一种初始布局和目标布局(为了使题目简单,设目标状态如下),找到一种从初始布局到目标布局最少步骤的移动方法。
123
804
765
解题思路:
\(h\)
函数可以定义为,不在应该在的位置的数字个数。
容易发现
\(h\)
满足以上两个性质,此题可以使用
\(A^*\)
算法求解。
参考代码:
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
#include <set>
using namespace std;
const int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
int fx, fy;
char ch;
struct matrix {
int a[5][5];
bool operator<(matrix x) const {
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
if (a[i][j] != x.a[i][j]) return a[i][j] < x.a[i][j];
return false;
}
} f, st;
int h(matrix a) {
int ret = 0;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
if (a.a[i][j] != st.a[i][j]) ret++;
return ret;
}
struct node {
matrix a;
int t;
bool operator<(node x) const { return t + h(a) > x.t + h(x.a); }
} x;
priority_queue<node> q; // 搜索队列
set<matrix> s; // 防止搜索队列重复
int main() {
st.a[1][1] = 1; // 定义标准表
st.a[1][2] = 2;
st.a[1][3] = 3;
st.a[2][1] = 8;
st.a[2][2] = 0;
st.a[2][3] = 4;
st.a[3][1] = 7;
st.a[3][2] = 6;
st.a[3][3] = 5;
for (int i = 1; i <= 3; i++) // 输入
for (int j = 1; j <= 3; j++) {
scanf(" %c", &ch);
f.a[i][j] = ch - '0';
}
q.push({f, 0});
while (!q.empty()) {
x = q.top();
q.pop();
if (!h(x.a)) { // 判断是否与标准矩阵一致
printf("%d\n", x.t);
return 0;
}
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
if (!x.a.a[i][j]) fx = i, fy = j; // 查找空格子(0号点)的位置
for (int i = 0; i < 4; i++) { // 对四种移动方式分别进行搜索
int xx = fx + dx[i], yy = fy + dy[i];
if (1 <= xx && xx <= 3 && 1 <= yy && yy <= 3) {
swap(x.a.a[fx][fy], x.a.a[xx][yy]);
if (!s.count(x.a))
s.insert(x.a),
q.push({x.a, x.t + 1}); // 这样移动后,将新的情况放入搜索队列中
swap(x.a.a[fx][fy], x.a.a[xx][yy]); // 如果不这样移动的情况
}
}
}
return 0;
}
\(k\)
短路
。
按顺序求一个有向图上从结点
\(s\)
到结点
\(t\)
的所有路径最小的前任意多(不妨设为
\(k\)
)个。
解题思路:
很容易发现,这个问题很容易转化成用
\(A^*\)
算法解决问题的标准程式。
初始状态为处于结点
\(s\)
,最终状态为处于结点
\(t\)
,距离函数为从
\(s\)
到当前结点已经走过的距离,估价函数为从当前结点到结点
\(t\)
至少要走过的距离,也就是当前结点到结点
\(t\)
的最短路。
就这样,我们在预处理的时候反向建图,计算出结点
\(t\)
到所有点的最短路,然后将初始状态塞入优先队列,每次取出
\(f(x) = g(x) + h(x)\)
最小的一项,计算出其所连结点的信息并将其也塞入队列。当你第
\(k\)
次走到结点
\(t\)
时,也就算出了结点
\(s\)
到结点
\(t\)
的
\(k\)
短路。
由于设计的距离函数和估价函数,每个状态需要存储两个参数,当前结点
\(x\)
和已经走过的距离
\(v\)
。
我们可以在此基础上加一点小优化:由于只需要求出第
\(k\)
短路,所以当我们第
\(k + 1\)
次或以上走到该结点时,直接跳过该状态。因为前面的
\(k\)
次走到这个点的时候肯定能因此构造出
\(k\)
条路径,所以之后再加边更无必要。
参考代码:
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int maxn = 5010;
const int maxm = 400010;
const double inf = 2e9;
int n, m, k, u, v, cur, h[maxn], nxt[maxm], p[maxm], cnt[maxn], ans;
int cur1, h1[maxn], nxt1[maxm], p1[maxm];
double e, ww, w[maxm], f[maxn];
double w1[maxm];
bool tf[maxn];
void add_edge(int x, int y, double z) { // 正向建图函数
cur++;
nxt[cur] = h[x];
h[x] = cur;
p[cur] = y;
w[cur] = z;
}
void add_edge1(int x, int y, double z) { // 反向建图函数
cur1++;
nxt1[cur1] = h1[x];
h1[x] = cur1;
p1[cur1] = y;
w1[cur1] = z;
}
struct node { // 使用A*时所需的结构体
int x;
double v;
bool operator<(node a) const { return v + f[x] > a.v + f[a.x]; }
};
priority_queue<node> q;
struct node2 { // 计算t到所有结点最短路时所需的结构体
int x;
double v;
bool operator<(node2 a) const { return v > a.v; }
} x;
priority_queue<node2> Q;
int main() {
scanf("%d%d%lf", &n, &m, &e);
while (m--) {
scanf("%d%d%lf", &u, &v, &ww);
add_edge(u, v, ww); // 正向建图
add_edge1(v, u, ww); // 反向建图
}
for (int i = 1; i < n; i++) f[i] = inf;
Q.push({n, 0});
while (!Q.empty()) { // 计算t到所有结点的最短路
x = Q.top();
Q.pop();
if (tf[x.x]) continue;
tf[x.x] = true;
f[x.x] = x.v;
for (int j = h1[x.x]; j; j = nxt1[j]) Q.push({p1[j], x.v + w1[j]});
}
k = (int)e / f[1];
q.push({1, 0});
while (!q.empty()) { // 使用A*算法
node x = q.top();
q.pop();
cnt[x.x]++;
if (x.x == n) {
e -= x.v;
if (e < 0) {
printf("%d\n", ans);
return 0;
}
ans++;
}
for (int j = h[x.x]; j; j = nxt[j])
if (cnt[p[j]] <= k && x.v + w[j] <= e) q.push({p[j], x.v + w[j]});
}
printf("%d\n", ans);
return 0;
}
注:对于
\(k\)
短路问题,原题已经可以构造出数据使得
\(A^*\)
算法无法通过,故本题思路仅供参考,
\(A^*\)
算法非正解,正解为可持久化可并堆做法。
参考资料与注释
\(^1\)
: 此处的
\(h\)
意为
\(\text{heuristic}\)
。详见
启发式搜索 - 维基百科
和
\(A^* \text{search algorithm - Wikipedia}\)
的 Bounded relaxation 一节。

