Transformer
在计算机视觉任务中表现出了令人鼓舞的性能，包括图像超分辨率（
SR
）。然而，流行的基于
Transformer
的
SR
方法通常采用具有二次计算复杂度的窗口自注意力机制，导致固定的小窗口，限制了感受野的范围。论文提出了一种将基于
Transformer
的
SR
网络转换为分层
Transformer
（
HiT-SR
）的通用策略，利用多尺度特征提升
SR
性能，同时保持高效设计。具体而言，首先用扩展的分层窗口替代常用的固定小窗口，以聚合不同尺度的特征并建立长距离依赖关系。考虑到大窗口所需的密集计算，进一步设计了一种具有线性复杂度的空间通道相关方法，以窗口大小高效地从分层窗口中收集空间和通道信息。大量实验验证了
HiT-SR
的有效性和效率，改进版本的
SwinIR-Light
、
SwinIR-NG
和
SRFormer-Light
在参数、
FLOPs
和速度方面取得了最先进的
SR
结果（约
7
倍）。

来源：晓飞的算法工程笔记 公众号，转载请注明出处

论文: HiT-SR: Hierarchical Transformer for Efficient Image Super-Resolution

Introduction

图像超分辨率（
SR
）是一项经典的低级视觉任务，旨在将低分辨率（
LR
）图像转换为具有更好视觉细节的高分辨率（
HR
）图像。如何解决不适定的
SR
问题引起了数十年的广泛关注。许多流行的方法采用卷积神经网络（
CNN
）来学习
LR
输入与
HR
图像之间的映射。尽管已取得显著进展，但基于
CNN
的方法通常侧重于通过卷积利用局部特征，往往在聚合图像中的长距离信息方面表现不足，从而限制了基于
CNN
的
SR
性能。

视觉
Transformer
的最新发展为建立长程依赖关系提供了一种有前景的解决方案，这为许多计算机视觉任务（包括图像超分辨率）带来了好处。在流行的基于
Transformer
的
SR
方法中，一个重要的组件是窗口自注意力（
W-SA
）。通过将局部性引入自注意力，
W-SA
机制不仅更好地利用了输入图像中的空间信息，还减轻了处理高分辨率图像时的计算负担。然而，目前的基于
Transformer
的
SR
方法通常采用固定的小窗口尺寸，例如
SwinIR
中的
\(8\times8\)
。将感受野限制在单一尺度，阻碍了网络收集多尺度信息，如局部纹理和重复模式。此外，
W-SA
对窗口大小的二次计算复杂度也使得在实际中扩大感受野变得不可承受。

为了减轻计算开销，以往的尝试通常减少通道数以支持大窗口，例如
ELAN
中的
group-wise
多尺度自注意力（
GMSA
）的通道分割和
SRFormer
中
permuted
自注意力块（
PSA
）的通道压缩。然而，这些方法不仅面临空间信息与通道信息之间的权衡，而且对窗口大小仍然保持二次复杂性，限制了窗口扩展（在
ELAN
中最大为
\(16\times16\)
，在
SRFormer
中为
\(24\times24\)
，而在论文的方法中则可达到
\(64\times64\)
及更大）。因此，如何在保持计算效率的同时有效聚合多尺度特征，仍然是基于
Transformer
的
SR
方法面临的一个关键问题。

为此，论文开发了一种通用策略，将流行的基于
Transformer
的
SR
网络转换为高效图像超分辨率的层级
Transformer
（
HiT-SR
）。受到多尺度特征聚合在超分辨率任务中成功的启发，论文首先提出用扩展的层级窗口替换
Transformer
层中的固定小窗口，使得
HiT-SR
能够利用逐渐增大感受野的信息丰富的多尺度特征。为了应对处理大窗口时
W-SA
计算负担的增加，论文进一步设计了一种空间-通道相关（
spatial-channel correlation
，
SCC
）方法，以高效聚合层级特征。具体而言，
SCC
由一个双特征提取（
dual feature extraction
，
DFE
）层组成，通过结合空间和通道信息来改善特征投影，还有空间和通道自相关（
S-SC
和
C-SC
）方法，以高效利用层级特征。其计算复杂度与窗口大小呈线性关系，更好地支持窗口扩展。此外，与传统的
W-SA
采用硬件效率较低的
softmax
层和耗时的窗口平移操作不同，
SCC
直接使用特征相关矩阵进行变换，并使用层级窗口进行感受野扩展，从而在保持功能性的同时提升了计算效率。

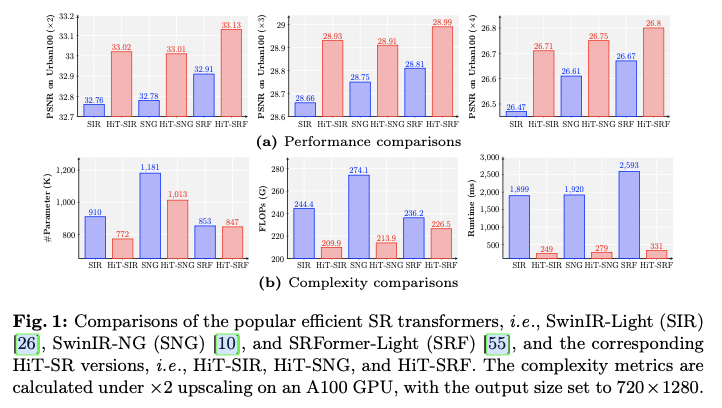
总体而言，论文的主要贡献有三个方面：

  1. 提出了一种简单而有效的策略，即
    HiT-SR
    ，将流行的基于
    Transformer
    的超分辨率方法转换为层级
    Transformer
    ，通过利用多尺度特征和长距离依赖关系来提升超分辨率性能。

  2. 设计了一种空间-通道相关方法，以高效利用空间和通道特征，其计算复杂度与窗口大小呈线性关系，从而实现对大层级窗口的利用，例如
    \(64\times64\)
    窗口。

  3. 将
    SwinIR-Light
    、
    SwinIR-NG
    和
    SRFormer-Light
    转换为
    HiT-SR
    版本，即
    HiT-SIR
    、
    HiT-SNG
    和
    HiT-SRF
    ，取得了更好的性能，同时参数和
    FLOPs
    更少，并实现了约
    7
    倍的速度提升。

Method

Hierarchical Transformer

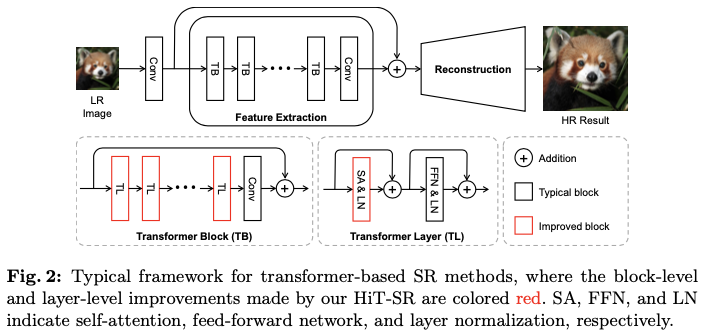
如图
2
所示，流行的基于
Transformer
的超分辨率框架通常包括卷积层，从低分辨率输入图像
\(I_{LR} \in \mathbb{R}^{3\times H\times W}\)
中提取浅层特征
\(F_{S} \in \mathbb{R}^{C\times H\times W}\)
，特征提取模块通过
Transformer
块（
TBs
）聚合深层图像特征
\(F_{D} \in \mathbb{R}^{C\times H\times W}\)
，以及重建模块从浅层和深层特征恢复高分辨率图像
\(I_{HR} \in \mathbb{R}^{3\times sH\times sW}\)
（
\(s\)
表示放大因子）。在特征提取模块中，
TBs
通常是由级联的
Transformer
层（
TLs
）和后续的卷积层构成，其中每个
TL
包括自注意力（
SA
）、前馈网络（
FFN
）和层归一化（
LN
）。由于自注意力的计算复杂度与输入大小呈二次关系，因此在
TL
中通常采用窗口划分来限制自注意力的作用于局部区域，这被称为窗口自注意力（
W-SA
）。尽管
W-SA
缓解了计算负担，但其感受野被限制在较小的局部区域，从而阻碍了超分辨率网络利用长距离依赖关系和多尺度信息。

为了高效聚合层级特征，论文提出了一种通用策略，将上述超分辨率框架转换为层级
Transformer
。如图
2
所示，主要在两个方面进行了改进：

  1. 在块级别对不同的
    TLs
    应用层级窗口，而不是对所有
    TLs
    使用固定的小窗口大小，从而使
    HiT-SR
    能够建立长距离依赖关系并聚合多尺度信息。
  2. 为了克服大窗口带来的计算负担，用一种新颖的空间-通道关联（
    SCC
    ）方法替代
    TLs
    中的
    W-SA
    ，这种方法更好地支持以线性计算复杂度进行窗口缩放。

基于上述策略，
HiT-SR
不仅通过利用层级特征获得了更好的性能，还得益于
SCC
保持了计算效率。

Block-Level Design: Hierarchical Windows

在块级别，为不同的
TLs
分配层级窗口，以收集多尺度特征。给定一个基础窗口大小
\(h_{B}\times w_{B}\)
，为第
\(i\)
个
TL
设置窗口大小
\(h_i\times w_i\)
为

\[\begin{equation}
h_i = \alpha_i h_{B},\quad w_i = \alpha_i w_{B},
\end{equation}
\]

其中
\(\alpha_i>0\)
是第
\(i\)
个
TL
的层级比率。

  • Expanding Windows

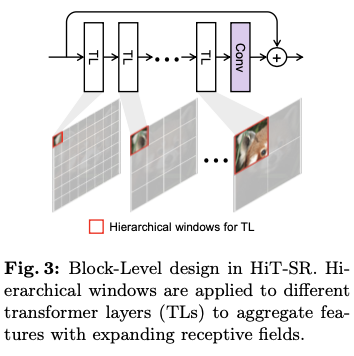
为了更好地聚合层级特征，采用一种扩展策略来安排窗口。如图
3
所示，首先在初始层使用小窗口大小，从局部区域收集最相关的特征，然后逐渐扩大窗口大小，以利用从长距离依赖中获得的信息。

之前的方法通常对固定的小窗口应用平移和掩码操作以扩大感受野，但这些操作在实践中耗时且效率低下。与它们相比，论文的方法直接利用级联的
TLs
形成一个层级特征提取器，使得小到大的感受野在保持整体效率的同时得以实现。
HiT-SR
方法相较于原始模型具有约
7
倍的速度提升，并且性能更佳。

Layer-Level Design: Spatial-Channel Correlation

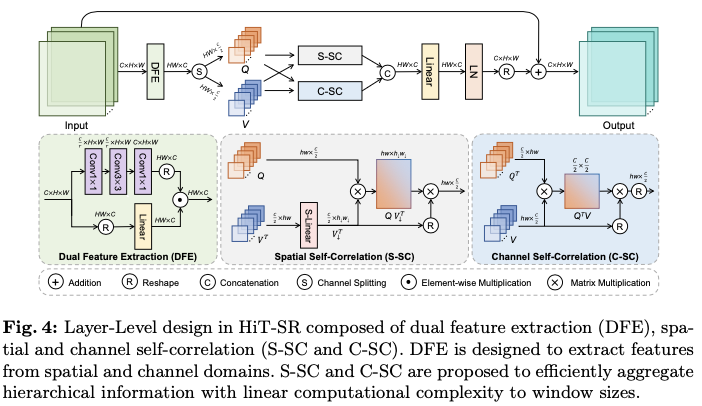
在层级水平上，论文提出了空间-通道相关性（
SCC
），以高效利用来自层级输入的空间和时间信息。如图
4
所示，
SCC
主要由双特征提取（
DFE
）、空间自相关（
S-SC
）和通道自相关（
C-SC
）组成。此外，与常用的多头策略不同，
S-SC
和
C-SC
应用了不同的相关头策略，以更好地利用图像特征。

  • Dual Feature Extraction

线性层通常用于特征投影，只提取通道信息而忽略了空间关系的建模。相反，论文提出了带有双分支设计的双特征提取（
DFE
），以利用来自两个领域的特征。如图
4
所示，
DFE
由一个卷积分支来利用空间信息和一个线性分支来提取通道特征组成。给定输入特征
\(X \in \mathbb{R}^{C\times H\times W}\)
，
DFE
的输出计算为

\[\begin{equation}
\begin{aligned}
&\operatorname{DFE}(X) = X_{ch} \odot X_{sp},\quad \text{with}
\\
X&_{ch} = \operatorname{Linear}(X),\ X_{sp} = \operatorname{Conv}(X),
\end{aligned}
\end{equation}
\]

其中，
\(\odot\)
表示逐元素相乘。
reshape
的通道特征
\(X_{ch} \in \mathbb{R}^{HW\times C}\)
和空间特征
\(X_{sp} \in \mathbb{R}^{HW\times C}\)
分别通过线性层和卷积层捕获。在空间分支中，使用一个沙漏结构堆叠三层卷积层，并将隐藏维度按比例
\(r\)
减小以提高效率。最后，空间特征和通道特征通过相乘相互作用，生成
DFE
输出。

与通过线性投影预测查询、键和值的标准
SA
方法不同，将键与值等同，因为它们都反映了输入特征的内在属性，仅通过对
DFE
输出进行拆分来生成查询
\(Q\in \mathbb{R}^{HW\times \frac{C}{2}}\)
和值
\(V \in \mathbb{R}^{HW\times \frac{C}{2}}\)
，如图
4
所示。

\[\begin{equation}
[Q, V] = \operatorname{DFE}(X),
\end{equation}
\]

这减少了由于键生成引起的信息冗余。然后，根据分配的窗口大小将查询和键划分为不重叠的窗口，例如，对于第
\(i\)
个
TL
，有
\(Q_i,\ V_i\in \mathbb{R}^{h_{i}w_{i}\times \frac{C}{2}}\)
（为了简化，省略了窗口的数量），并使用划分后的查询和值进行后续的自相关计算。

  • Spatial Self-Correlation

与
W-SA
相比，
S-SC
以高效的方式聚合空间信息。考虑到层级化策略中扩展的窗口大小，首先通过在空间维度上应用线性层（称为
S-Linear
）自适应地总结不同
TL
中值
\(V_i\)
的空间信息，即，

\[\begin{equation}
V_{\downarrow,i}^T = \operatorname{S-Linear}_{i}(V_i^T),
\end{equation}
\]

其中
\(V_{\downarrow,i}\in \mathbb{R}^{h_\downarrow w_\downarrow \times \frac{C}{2}}\)
表示投影后的值，具有

\[\begin{equation}
\left[h_\downarrow, w_\downarrow \right]= \left\{
\begin{array}{ll}
\left[h_i, w_i\right], & \text { if } \alpha_i \leq 1, \\
\left[h_B, w_B\right], & \text { if } \alpha_i > 1.
\end{array}\right.
\end{equation}
\]

因此，
HiT-SR
能够从大窗口中总结高层信息，即
\(\alpha_i> 1\)
，同时保留小窗口中的细粒度特征，即
\(\alpha_i\leq 1\)
。随后，基于
\(Q_i\)
和
\(V_{\downarrow,i}\)
计算
S-SC
，如下所示：

\[\begin{equation}
\operatorname{S-SC}(Q_i, V_{\downarrow,i}) = \left(\frac{Q_i V_{\downarrow,i}^T}{D} + B\right)\cdot V_{\downarrow,i},
\end{equation}
\]

其中
\(B\)
表示相对位置编码，常数分母
\(D=\frac{C}{2}\)
用于归一化。与标准的
W-SA
相比，
S-SC
在效率和复杂性上显示出优势：

  1. 利用相关图而不是注意力图来聚合信息，去掉了在硬件上效率低下的
    softmax
    操作，以提高推理速度。
  2. S-SC
    支持大窗口，具有线性的计算复杂度与窗口大小相关。假设输入包含
    \(N\)
    个窗口，每个窗口在
    \(\mathbb{R}^{hw\times C}\)
    空间中，那么
    W-SA
    和
    S-SC
    所需的
    mult-add
    操作数量分别为：

\[\begin{equation}
\begin{aligned}
&\operatorname{Mult-Add}(\operatorname{W-SA})= 2NC(hw)^2,
\\
&\operatorname{Mult-Add}(\operatorname{S-SC})= 2NCh_\downarrow w_\downarrow hw,
\end{aligned}
\end{equation}
\]

其中前者与窗口大小
\(hw\)
成平方关系。由于
\(h_\downarrow w_\downarrow\)
受到固定基准窗口大小
\(h_B w_B\)
的上限限制，
S-SC
的计算复杂性与窗口大小成线性关系，从而有利于窗口的放大。

  • Channel Self-Correlation

除了空间信息，论文进一步设计了
C-SC
以从通道域中聚合特征，如图
4
所示。给定第
\(i\)
个
TL
中的分区查询和数值，
C-SC
的输出为：

\[\begin{equation}
\operatorname{C-SC}(Q_i, V_i) = \frac{Q_i^T V_i}{D_i} \cdot V^T_i,
\end{equation}
\]

其中分母
\(D_i = h_i w_i\)
。与当前普遍采用的转置注意力进行通道聚合相比，
C-SC
利用层级化窗口，并利用丰富的多尺度信息来提升超级分辨率 (
SR
) 性能。在计算复杂性方面，在
\(\mathbb{R}^{N\times hw \times C}\)
空间中的输入下，
C-SC
所需的
mult-add
操作数量为：

\[\begin{equation}
\operatorname{Mult-Add}(\operatorname{C-SC}) = 2N C^2 hw
\end{equation}
\]

结合公式
7
和
9
，空间-通道相关性的复杂度保持与窗口大小成线性关系，如表
1
所示，使得可扩展窗口能够充分利用层级信息。

  • Different Correlation Head

多头策略通常在自注意力 (
SA
) 中被采用，以从不同的表示子空间中聚集信息，并且在处理空间信息时表现出了良好的性能。然而，在处理通道信息时，多头策略反而限制了通道信息聚合的感受野，即每个通道只能与有限的一组其他通道进行交互，这导致了次优的表现。

为了解决这个问题，论文提议在
S-SC
中应用标准的多头策略，但在
C-SC
中使用单头策略，从而实现全面的通道交互。因此，
S-SC
可以通过多头策略利用来自不同通道子空间的信息，而
C-SC
则可以通过层级化窗口利用来自不同空间子空间的信息。

Experiments and Analysis

  • Implementation Details

将
HiT-SR
策略应用于流行的超级分辨率 (
SR
) 方法
SwinIR-Light
，以及最近的最先进的
SR
方法
SwinIR-NG
和
SRFormer-Light
，对应于本文中的
HiT-SIR
、
HiT-SNG
和
HiT-SRF
。为了公平地验证有效性和适应性，控制每种方法转换为
HiT-SR
版本所需的更改最小，并且对所有
SR Transformer
应用相同的超参数设置。

具体而言，遵循
SwinIR-Light
的原始设置，将所有
HiT-SR
改进模型的
TB
数量、
TL
数量、通道数量和头数量分别设置为
4
、
6
、
60
和
6
。基础窗口大小
\(h_{B}\times w_{B}\)
设置为广泛采用的值，即
\(8\times8\)
，并且将每个
TB
中的
6
个
TL
的层级化比例设置为
\([0.5, 1, 2, 4, 6, 8]\)
。

对
HiT-SIR
、
HiT-SNG
和
HiT-SRF
应用相同的训练策略。所有模型均基于
PyTorch
实现，并在
\(64\times64\)
的图像块大小和
\(64\)
的批量大小下训练
500K
次迭代。模型优化采用
\(L_1\)
损失和
Adam
优化器 (
\(\beta_1=0.9\)
和
\(\beta_2=0.99\)
)。将初始学习率设置为
\(5\times10^{-4}\)
，并在 [
250K
,
400K
,
450K
,
475K
] 次迭代时将其减半。在模型训练过程中，我们还随机利用
90
°、
180
° 和
270
° 的旋转以及水平翻转进行数据增强。

  • Result



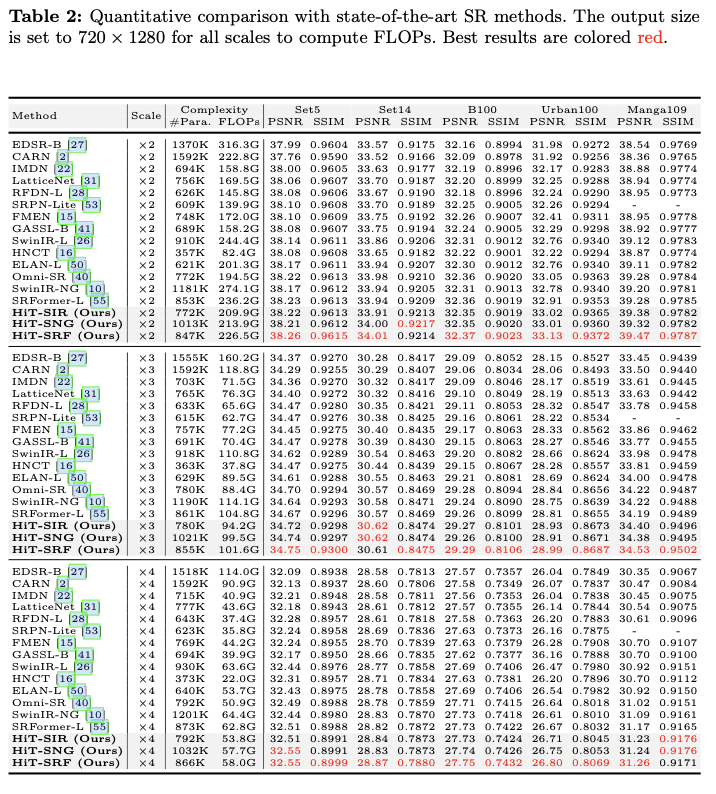
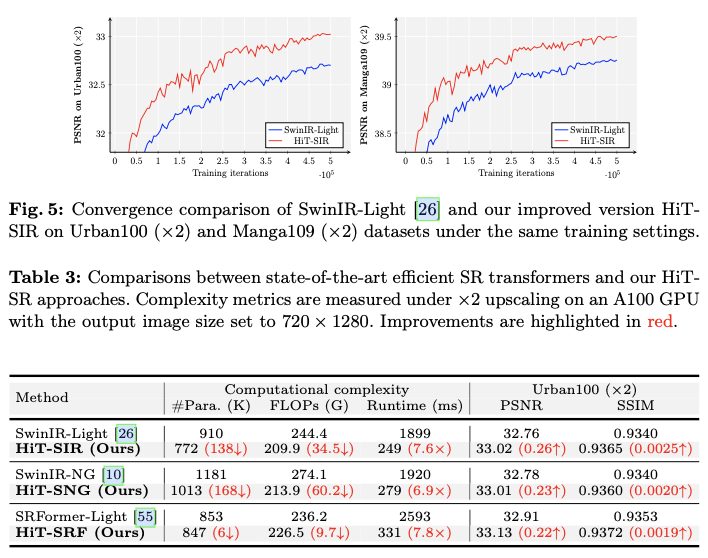
如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】

work-life balance.

标签: none

添加新评论