门罗币隐私保护之隐形地址
主页
微信公众号:密码应用技术实战
博客园首页:
https://www.cnblogs.com/informatics/
GIT地址:
https://github.com/warm3snow
简介
从2009年比特币的诞生,区块链技术已经发展了十多年,区块链技术的应用也从最初的数字货币扩展到金融、供应链、医疗、物联网等多个领域。区块链技术的核心是去中心化、不可篡改、匿名性等特性,其中匿名性是区块链技术的重要特性之一,它可以保护用户的隐私,防止用户的交易信息被泄露。在区块链技术中,匿名地址是用户的重要身份标识,用户可以通过匿名地址进行资产托管、资产转账等操作,而不用暴露自己的真实身份。
在比特币中过,用户可以通过私钥生成公钥,再通过公钥生成比特币地址,然后通过比特币地址进行交易,而不用暴露自己的真实身份。虽然比特币地址(如:1BvBMSEYstWetqTFn5Au4m4GFg7xJaNVN2)具有一定的匿名性,但是比特币地址是公开的,通过大数据手段,可以将该地址相关的交易信息进行关联,只要有一个交易地址被关联到了用户的真实身份,那么用户的所有交易信息都会被暴露,因此比特币匿名性较差。
随着区块链技术的发展,区块链用户隐私的研究也逐渐增多,其中Zcash、Monero等匿名币的研究较为深入,它们通过零知识证明、环签名、隐形地址等技术,实现了更好的匿名性和用户隐私。本文及系列文章将重点介绍
门罗币
的隐私保护技术,如:隐形地址、环签名、机密交易等。
术语介绍
椭圆曲线定义
椭圆曲线(Elliptic Curve)是一种数学曲线,它的一般代数表达形式为:
\]
其中,
\(a, b\)
是椭圆曲线的参数,
\((x, y)\)
是椭圆曲线上的点。
在密码学中,椭圆曲线通常定义在有限域
\(F_p\)
上, 其中
\(p\)
是一个大素数。此时,
\(x\)
和
\(y\)
的取值范围是
\(0\)
到
\(p-1\)
。具体来说,
\(x\)
和
\(y\)
都是有限域
\(F_p\)
中的元素,满足椭圆曲线方程,这样的方程我们也称为
有限域上的椭圆曲线
。构造在椭圆曲线上的密码学我们称为
椭圆曲线密码学
,英文缩写为ECC(Elliptic Curve Cryptography)。
有限域上的椭圆曲线有以下几个重要的性质:
- 单位元
:椭圆曲线上的单位元
\(O\)
是一个特殊的点,它是椭圆曲线上的无穷远点,单位元
\(O\)
是椭圆曲线上的一个特殊点,它满足
\(P + O = P\)
,
\(P - P = O\)
,
\(O + O = O\) - 逆元
:椭圆曲线上的逆元是指给定一个点
\(P\)
,求解满足
\(Q = -P\)
的点
\(Q\)
,其中
\(Q\)
是椭圆曲线上的另一个点 - 点加
:椭圆曲线上的点加法是指给定两个点
\(P, Q\)
,
\(P \neq Q\)
, 求解它们的和
\(R = P + Q\)
, 其中
\(R\)
是椭圆曲线上的另一个点 - 生成元
:椭圆曲线上的生成元是指给定一个点
\(G\)
,通过不断地对
\(G\)
进行倍乘运算,可以得到椭圆曲线上的所有点 - 倍乘
:椭圆曲线上的点倍乘是指给定一个点
\(P\)
和一个整数
\(k\)
,求解满足
\(Q = kP = \sum_{i=1}^{k}P\)
的点
\(Q\)
,其中
\(Q\)
是椭圆曲线上的另一个点
离散对数困难问题
是指在有限域的椭圆曲线上,给定椭圆曲线上的一个点
\(P\)
和另一个点
\(Q\)
,求解满足
\(Q = aG\)
的
\(a\)
值。(该问题是一个困难问题,目前没有有效的解决方案,也是椭圆曲线加密算法的安全基础)
匿名性定义
隐私和匿名是电子现金最重要的方面。与传统银行不同的是,区块链交易(或者说点对点支付)旨在不依赖于第三方。特别是,T. Okamoto 和 K. Ohta 描述了理想电子现金的几个标准,其中包括“隐私:交易双方的关系必须对任何人不可追踪”。根据他们的描述,完全匿名的电子现金模型必须满足的两个属性:
- 不可追踪性
(Untraceability):对于每一笔 incoming 交易,所有可能的发送者都是等概率的。这意味着,对于任何两个 incoming 交易,无法证明它们是由同一个人发送的。 - 不可链接性
(Unlinkability):对于任何两笔 outgoing 交易,无法证明它们是发送给同一个人的。即对于任何两个 outgoing 交易,无法证明它们是由同一个人收款的。
不幸的是,比特币并不满足不可追踪性要求。由于网络参与者之间发生的所有交易都是公开的,任何交易都可以明确地追溯到唯一的来源和最终收款者。即使两个参与者以间接方式交换资金,经过精心设计的路径查找方法也会揭示出来源和最终收款者。
虽然比特币可以提供不可链接性,但是它并不是默认的。用户必须小心地处理他们的地址,以确保不会在不同的交易中使用相同的地址。这是因为,如果两个交易都使用相同的地址,那么这两个交易就可以被链接在一起,从而揭示出用户的身份。
术语定义
- 公私钥对:公私钥对常见于非对称密码算法,在这些算法中,使用的密钥包含公钥和私钥。公钥公开,用于加密或签名验证;私钥保密,用于解密或签名。常见的非对称密码算法有RSA、ECC等。如在椭圆曲线中,
\(Q = aG\)
,其中
\(Q\)
是公钥,
\(a\)
是私钥 - 用户公私钥对/密钥对:用户公私钥对用
\((a, Q)\)
表示,其中
\(a\)
是用户的私钥,
\(Q\)
是用户的公钥。其中
\((a, Q)\)
被称为标准的椭圆曲线密钥对 - 门罗币用户密钥对:在门罗币中,用户密钥对包含两个标准的椭圆曲线密钥对
\((a, A)\)
和
\((b, B)\)
,不是一般性,后文中称
\((a, b)\)
为用户私钥,称
\((A, B)\)
为用户公钥
门罗币之隐形地址
在比特币和以太坊等经典区块链系统中,用户可以在不同交易中使用不同的地址来保证交易的不可链接性
比特币交易模型
如下:
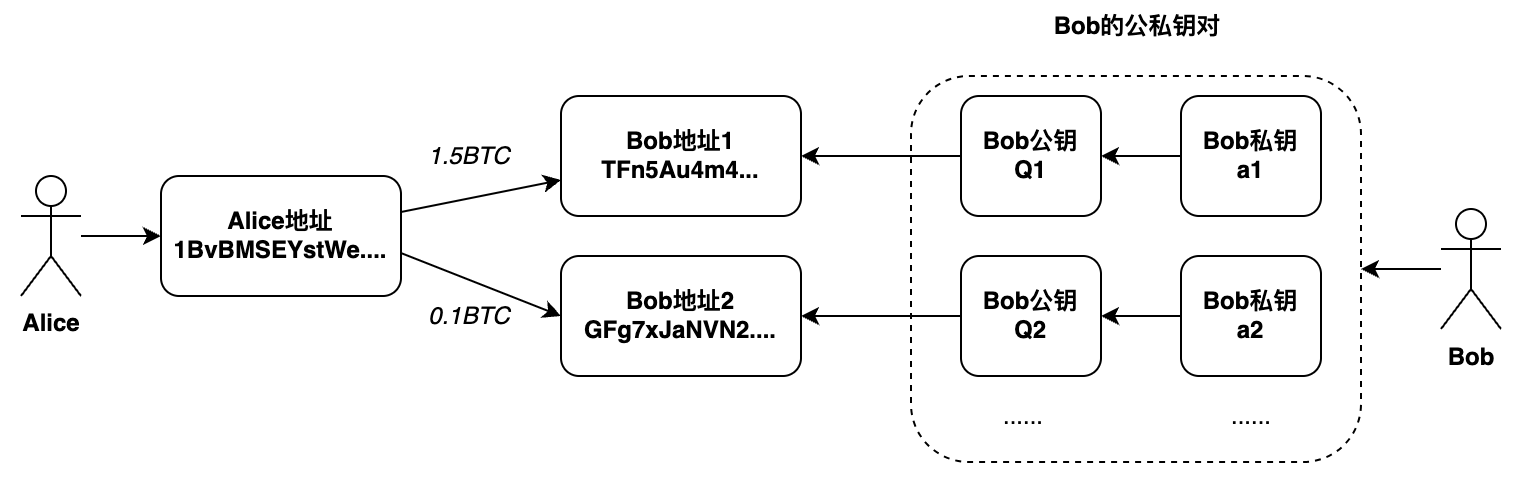
以上图为例,在比特币网络中,当Alice在给Bob进行2次转账时,使用了Bob不同的地址,对应不同的公私钥对。比特币交易具有如下特点:
- 为了保证用户的隐私,Bob需要每次生成一个新的比特币地址(对应新的公私钥对),这样可以保证每次交易的地址不同,从而保证交易的隐私性
- 比特币钱包需要维护一个地址池,每次生成一个新的地址,就需要将该地址加入到地址池中,这样会增加钱包的存储空间
- 由于钱包存储空间有限,限制了用户生成地址的数量,从而不可避免导致在不同交易中使用相同的地址,无法保证地址的不可链接性
- 不同的地址之间相互独立,无法关联,能够保证交易的不可链接性,从而保证用户的隐私性
门罗币使用了一种匿名地址技术,称为
隐形地址(stealth address)
,隐身地址与实际收款人的用户唯一公私钥绑定,但只有发送方和收款方知道两者之间的关联。对于用户的每一笔转账交易,收款方可以使用不同的隐形地址,从而保证了用户交易的
不可链接性
门罗币交易模型
如下:
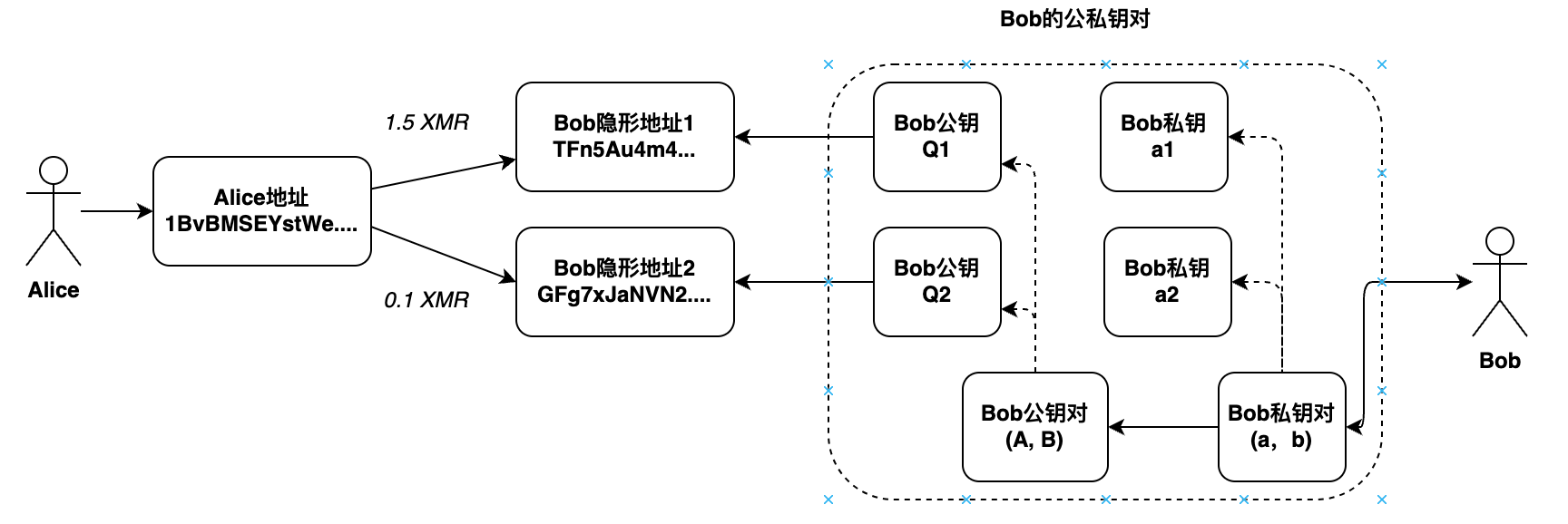
以上图为例,在门罗币网络中,当Alice在给Bob进行2次转账时,使用了Bob不同的地址,对应不同的公私钥对,但这些不同的公私钥对都是由相同的密钥对派生得到。门罗币交易具有如下特点:
- 门罗币用户只需要维护两个标准的公私钥对
\((a, A)\)
和
\((b, B)\)
,在每次收款时,基于用户的公私钥对生成一个隐形地址,用于收款。如:
\(Q_1\)
和
\(Q_2\)
是基于用户公私钥对生成的临时公钥,对应私钥为
\(a_1\)
和
\(a_2\) - 隐形地址不需要事先生成和本地存储,只需要在收款时,基于用户的公私钥对生成一个隐形地址即可,降低了钱包的存储空间
- 基于用户公私钥对可以生成多个隐形地址,每个隐形地址之间不可关联,从而保证了用户的隐私性
门罗币中的隐形地址是通过用户的公私钥对
\((a, A)\)
和
\((b, B)\)
生成的,通常用
\((a, b)\)
表示用户的私钥,用
\((A, B)\)
表示用户的公钥。隐形地址主要应用在门罗币
生成交易
和
接收交易
中,下面我们分别介绍隐形地址的生成和验证过程。
生成交易(转账)
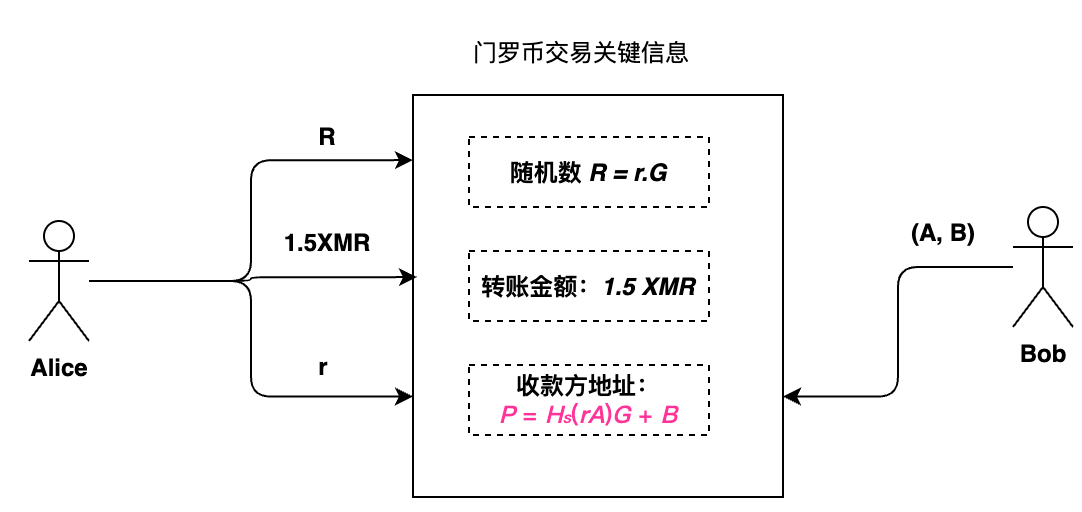
- Alice要向Bob转账, Alice首先生成随机数
\(r\)
, 并计算
\(R = rG\)
,作为交易的一部分 - Alice补充转账金额,如图中为
\(1.5 XMR\)
, 表示Alice向Bob转账
\(1.5\)
个门罗币 - Bob私下提供给Alice自己的公钥
\((A, B)\) - Alice基于Bob的公钥生成一个隐形地址
\(P = H_s(rA)G + B\)
, 其中
\(H_s\)
是哈希函数,
\(G\)
是椭圆曲线上的生成元 - Alice对交易信息
\((R, 1.5XMR, P)\)
进行签名,生成签名
\(S\)
,并将
\((R, 1.5XMR, P, S)\)
发送到门罗币网络中
值得注意的是,隐形地址
\(P\)
的随机性是由
\(r\)
决定的,而
\(r\)
是Alice生成的随机数,只有Alice知道,因此隐形地址的安全性依赖于Alice生成
\(r\)
的安全性
接收交易(收款)
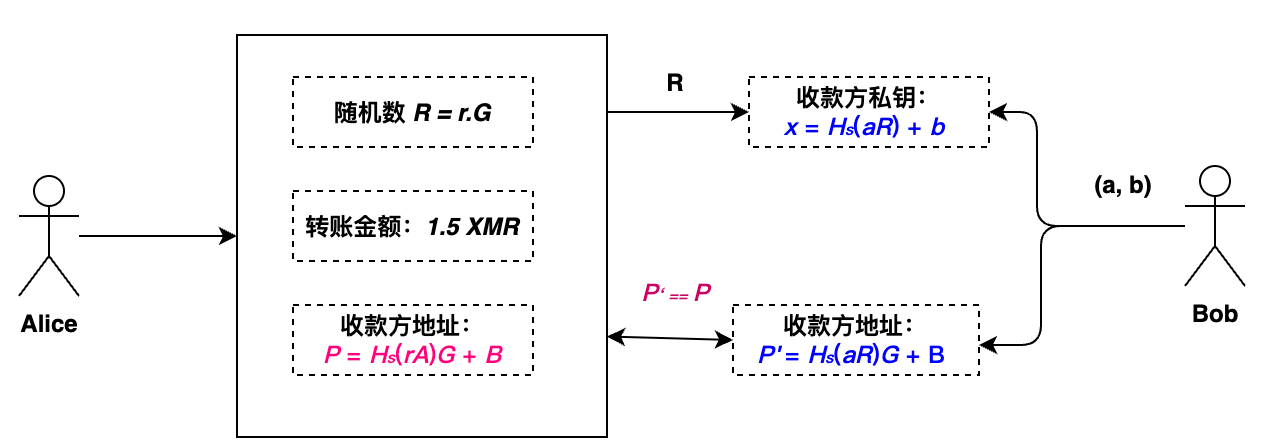
- Bob在区块链上查询到Alice的交易信息
\((R, 1.5XMR, P, S)\)
,并验证签名的有效性 - Bob基于自己的密钥
\((a, B)\)
,计算
\(P^{'} = H_s(aR)G + B\)
,并验证
\(P \stackrel{?}{=} P^{'}\)
,如果验证通过,则表示该交易是Bob的收款交易 - 同时当Bob需要花费该笔交易时,Bob可以使用自己的密钥
\((a, b)\)
,计算
\(x = H_s(aR) + b\)
,并使用
\(x\)
作为签名私钥,从而授权该交易
收款隐私性和正确性验证
- 隐私性:需要注意的是,由于只有Bob知道自己的私钥
\((a)\)
,因此只有Bob能够计算出
\(H_s(aR)\)
,从而计算出
\(P^{'}\)
,因此只有Bob能够确认该交易是自己的收款交易,保证了用户隐私性 - 正确性验证如下:
\]
\]
\]
\]
\]
因此,
\(P^{'} = P\)
,验证通过,表示Bob能够正确验证该交易是自己的收款交易
支出正确性验证
Bob要能够花费该笔资产,需要保证自己有
\(P\)
对应的私钥。Bob可以根据自己的私钥
\((a, b)\)
,计算
\(x = H_s(aR) + b\)
支出正确性验证如下:
\]
\]
\]
\]
\]
\]
因此,
\(P = xG\)
,表示
\(x\)
是
\(P\)
对应的私钥,Bob可以使用
\(x\)
作为签名私钥,从而授权对应资产的支出
视图密钥和支出密钥
从Bob收款和支出的过程中,我们可以看到Bob收款时只需要用到
\((a, B)\)
, 而支出时需要用到
\((a, b)\)
,按照使用场景,一般将
\((a, B)\)
称为
视图密钥
,将
\((a, b)\)
称为
支出密钥
- 视图密钥:用于收款,可以公开给监管结构或第三方,第三方可以通过视图密钥查看用户的交易记录,但是由于不知道全部的私钥
\((a, b)\)
,因此无法花费用户的资产 - 支出密钥:用于支出,只有用户自己知道,用于花费用户的资产
门罗币的隐形地址技术,为监管机构提供了一种有效的监管手段,既保护了用户的隐私,又满足了监管机构的监管需求。因此,在不少数字货币友好的国家和地区也开始尝试在主权数字货币中引入门罗币的隐形地址技术。
结语
隐形地址技术是门罗币的核心技术之一,实现了用户的隐私保护和监管需求。本文简单介绍了比特币和门罗币的交易模型,并详细介绍了门罗币的隐形地址技术,包括隐形地址的生成和验证过程。希望通过本文的介绍,读者能够了解门罗币的隐形地址技术,以及隐形地址技术的应用场景和优势。
下一篇文章将介绍门罗币的环签名技术,环签名技术是门罗币的另一个核心技术,它通过环签名技术,实现了交易的不可追踪性。