一文彻底弄清Redis的布隆过滤器

布隆过滤器（Bloom Filter）是一种空间效率极高的数据结构，用于快速判断一个元素是否在集合中。它能够节省大量内存，但它有一个特点：可能存在误判，即可能会认为某个元素存在于集合中，但实际上不存在；而对于不存在的元素，它保证一定不会误判。布隆过滤器适合在对存储空间要求极为严格，同时能接受少量误判的应用场景中使用。

1. 布隆过滤器的工作原理

布隆过滤器的核心思想是使用多个
哈希函数（Hash Functions）
和一个位数组（Bit Array）。其操作过程如下：

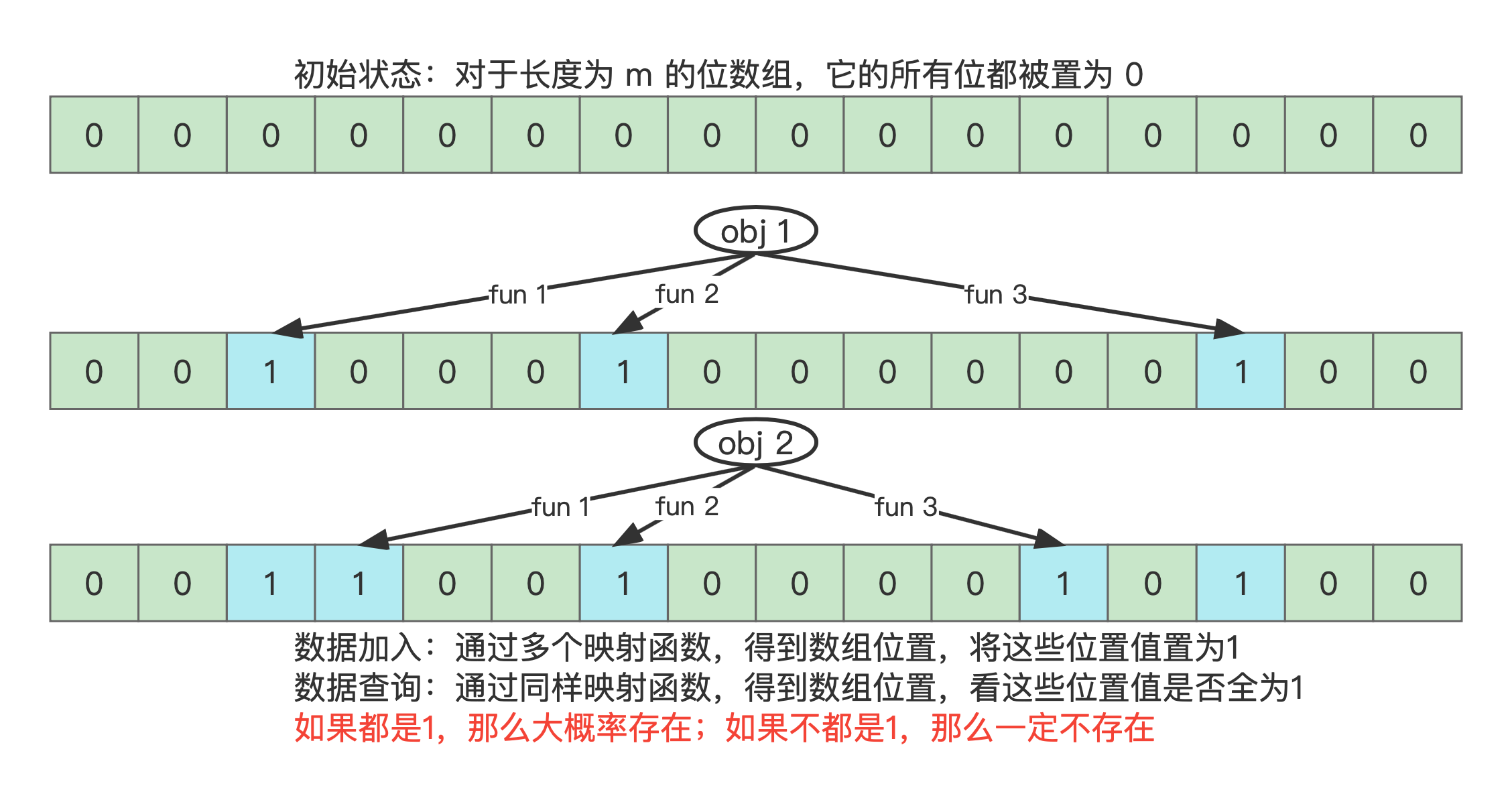
1.1 插入元素

• 当插入一个元素时，布隆过滤器会使用多个不同的哈希函数对该元素进行哈希计算，得到多个哈希值（位置索引），并将这些哈希值对应的位数组位置设置为
  1
  。
• 例如，一个元素经过 3 个哈希函数后，得到了 3 个不同的位置，布隆过滤器就在这 3 个位置上将位数组的值设为
  1
  。

1.2 查询元素

• 查询某个元素时，布隆过滤器会使用相同的哈希函数对该元素进行哈希计算，得到多个位置。如果所有这些位置的位都为
  1
  ，则布隆过滤器认为这个元素
  可能存在
  ；如果任意一个位置的位为
  0
  ，则可以确定这个元素
  一定不存在
  。

1.3 特点

• 可能存在误判
  ：布隆过滤器有可能出现误判，查询一个不存在的元素时，有小概率会因为位数组中的某些位被其他元素设为
  1
  ，而误认为这个元素存在。
• 不会漏判
  ：如果某个元素不存在，布隆过滤器一定不会误判其存在，即布隆过滤器查询某个元素是否存在时，若判断不存在，结果是可靠的。

2. 布隆过滤器的组成部分

2.1 位数组（Bit Array）

位数组是布隆过滤器的核心数据结构。它是一个长度为
m
的数组，每个位置上只能存储
0
或
1
。初始时，位数组中所有位置的值都为
0
。在插入元素时，哈希函数根据元素值生成若干个位置索引，并将这些索引对应的位设为
1
。

2.2 哈希函数（Hash Functions）

布隆过滤器使用多个哈希函数（通常是独立的哈希函数）来对元素进行哈希操作。每个哈希函数会生成一个不同的位数组索引，用于确定元素的存储位置。

• 选择的哈希函数应当具有较好的均匀性，确保哈希值能够均匀分布在位数组上，减少冲突。

2.3 哈希函数的数量（k 值）

k
表示用于每个元素的哈希函数的个数。哈希函数数量越多，误判的概率越低，但查询和插入的复杂度会增加。因此，
k
的数量一般选择一个合适的中间值，以在查询性能和误判率之间取得平衡。

2.4 位数组的长度（m 值）

m
是位数组的长度，位数组越长，误判率越低，但需要占用的内存也更多。因此，位数组的长度应该根据实际的业务需求和内存开销进行权衡设计。

3. 布隆过滤器的误判率

布隆过滤器的误判率是指在查询时，布隆过滤器错误地认为一个不存在的元素存在于集合中的概率。误判率随着集合中插入的元素数量的增加而增加，主要受到以下几个因素的影响：

• 位数组长度（m）
  ：位数组越长，误判率越低。
• 哈希函数数量（k）
  ：哈希函数数量适中时误判率最低，但数量过多会使得误判率增加。
• 元素数量（n）
  ：插入的元素越多，误判率越高，因为位数组中被设置为
  1
  的位越来越多，哈希函数的碰撞机会增大。

布隆过滤器的误判率计算公式如下： p=(1−e−k⋅nm)kp = \left( 1 - e^{- \frac{k \cdot n}{m}} \right)^kp=(1−e−mk⋅n)k

• p
  是误判率；
• k
  是哈希函数的数量；
• n
  是插入的元素数量；
• m
  是位数组的长度。

4. 布隆过滤器的优缺点

4.1 优点

• 高效的空间利用率
  ：布隆过滤器可以用较小的空间存储大量数据，尤其在元素数量很大时，它可以显著节省内存。
• 查询和插入操作的时间复杂度很低
  ：无论插入还是查询，布隆过滤器的时间复杂度都是 O(k)，即与哈希函数的数量成线性关系，速度非常快。
• 适合大规模数据过滤
  ：对于海量数据的存在性判断，布隆过滤器非常高效，适合在需要快速判断某个元素是否存在的场景中使用。

4.2 缺点

• 存在误判
  ：布隆过滤器可能会误判一个元素存在，即判断结果可能为“假阳性”（False Positive），这意味着虽然布隆过滤器认为某个元素存在，但实际上它并不存在。布隆过滤器不适合用于需要精准判断的场景。
• 无法删除元素
  ：布隆过滤器无法直接删除元素，因为哈希函数将多个元素映射到同一位数组位置，删除某个元素可能会导致其他元素的哈希结果失效。虽然有
  计数布隆过滤器
  （Counting Bloom Filter）可以支持删除操作，但其实现更加复杂。

5. 布隆过滤器的典型应用场景

5.1
缓存穿透防护

• 布隆过滤器最常见的应用之一就是防止

  缓存穿透

  。在 Redis 缓存场景中，用户请求的数据可能在缓存和数据库中都不存在，如果不加以防护，这些请求会直接打到数据库。通过布隆过滤器，可以在请求前判断元素是否可能存在于数据库中，从而减少无效的数据库查询。

  
  
  • 场景：
    一个电商系统中，用户可能会频繁查询一些并不存在的商品 ID。布隆过滤器可以用来存储所有合法商品 ID，在查询前进行判断，如果布隆过滤器中不存在，则可以直接返回空结果，而不必查询数据库和缓存。

5.2
垃圾邮件过滤

• 布隆过滤器可以用于垃圾邮件系统，用来快速判断某个电子邮件地址或 IP 是否在黑名单列表中。由于布隆过滤器的高效性，可以极大提高垃圾邮件检测的速度，并节省内存资源。

5.3
大数据去重

• 在大规模数据处理场景中，布隆过滤器可以用来检测某个元素是否已经出现过，从而实现去重操作。它特别适用于对内存要求严格的系统中，比如分布式爬虫系统中需要去重的 URL 处理。

5.4
数据库和存储系统

• 布隆过滤器被广泛应用于数据库和存储系统中，用于减少不必要的磁盘 I/O 操作。例如：
  
  • HBase
    使用布隆过滤器来加快查找速度，避免不必要的磁盘读取。
  • Cassandra
    使用布隆过滤器来判断某个 SSTable 是否包含某个键，从而减少磁盘扫描次数。

6. 布隆过滤器的扩展

6.1
计数布隆过滤器（Counting Bloom Filter）

计数布隆过滤器是一种支持删除操作的布隆过滤器。与标准布隆过滤器不同的是，计数布隆过滤器的位数组中的每个位置不再是二进制的
0
和
1
，而是一个计数器。当插入一个元素时，多个哈希函数对应的位上的计数器增加；当删除一个元素时，计数器相应减少。

计数布隆过滤器的缺点是需要更多的存储空间（因为每个位置是一个计数器），但它允许删除元素，这使得它适用于动态更新的场景。

6.2
分布式布隆过滤器

在大规模分布式系统中，布隆过滤器可以扩展为
分布式布隆过滤器
，即将位数组分布在多个节点上，并且每个节点负责一部分位数组的存储和哈希计算。这样可以提高系统的可扩展性，适应更大规模的数据集。

总结

布隆过滤器是一种空间效率极高的数据结构，适用于需要快速判断某个元素是否存在的场景，尤其适用于防止缓存穿透、垃圾邮件过滤、大数据去重等场景。虽然它存在一定的误判率，但其出色的空间效率和查询性能使其成为许多大规模应用中的重要工具。