来源：晓飞的算法工程笔记 公众号，转载请注明出处

论文: Exploring the Benefit of Activation Sparsity in Pre-training

创新点

  • 研究了激活属性在预训练过程中的变化，发现
    Transformer
    在大多数预训练过程中表现出稀疏激活，同时激活相关性随着训练的进行而不断演变。
  • 提出了可切换的稀疏-密集学习（
    Switchable Sparse-Dense Learning
    ，
    SSD
    ），在预训练过程中自适应地在基于专家混合（
    Mixtures-of-Experts
    ,
    MoE
    ）稀疏训练和传统的密集训练之间切换，充分利用稀疏训练的效率，避免了稀疏训练的静态激活相关性。
  • 与密集训练相比，
    SSD
    在相同模型规模下实现了可比的性能，并降低了预训练成本。
  • 使用
    SSD
    训练的模型可以直接作为
    MoE
    模型用于稀疏推理，并且在推理速度上可实现与密集模型相同的性能，速度提升可达
    \(2\times\)
    。

内容概述

预训练的
Transformer
本质上具有稀疏激活的特征，即每个
token
只有一小部分神经元被激活。尽管稀疏激活在后训练（推理）方法中得到了探索，但其在预训练中的潜力仍未被发掘。

论文研究了
Transformer
在预训练过程中的激活情况，发现模型在预训练的早期阶段变得稀疏激活，随后在这种稀疏状态中稳定下来。尽管这表明稀疏激活是一个普遍现象，但激活模式仍然是动态的：对于某个输入，被激活的神经元集合在不同的预训练阶段之间存在变化。因此，针对预训练的稀疏训练方法应该适应激活模式的变化。

基于这些观察，论文提出了可切换稀疏-密集学习（
Switchable Sparse-Dense Learning
，
SSD
），利用稀疏激活现象加速
Transformer
的预训练，并提高推理效率。

SSD
包含两种训练阶段：

  • 原始的密集训练，有助于激活模式的演变。
  • 稀疏训练，旨在在激活模式稳定之后有效优化模型参数。

在整个预训练过程中，
SSD
在这两个阶段之间切换。具体而言，当激活稀疏性增加并且激活模式变得稳定时，通过将密集模型转换为稀疏激活专家混合模型（
Sparsely-activated Mixture-of-Experts
，
SMoE
）来切换到稀疏训练，从而有效近似原始密集模型。此外，最终的密集模型熟悉稀疏计算形式，这对后续的稀疏推理是有利的。

与传统的密集训练相比，
SSD
在相同模型大小和更少的预训练成本下实现了可比的性能，在
FLOPs
上实现了高达
\(1.44\times\)
的加速。此外，使用
SSD
预训练的模型可以作为
SMoE
模型进行推理，而无需任何额外训练，同时将前馈网络的推理时间减少了高达
\(2\times\)
，且性能与密集预训练模型相当。

SSD

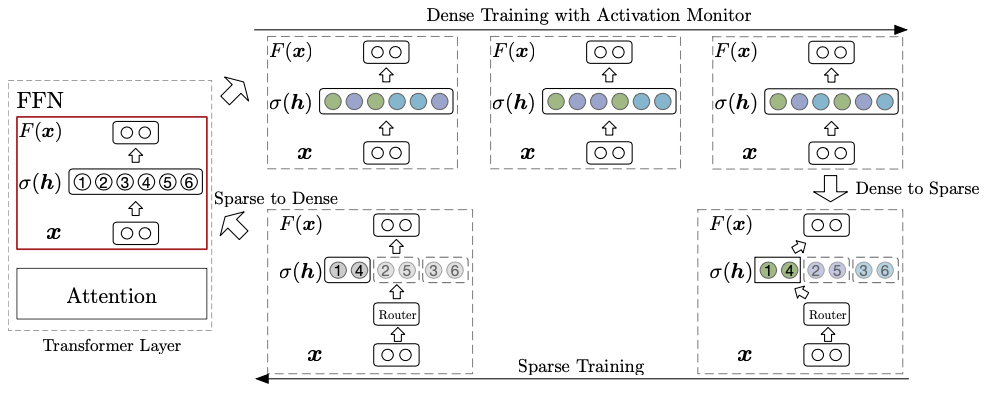
SSD
专注于加速
Transformer
中的前馈网络（通常占总计算量的
60%
以上），通过在预训练阶段切换稀疏和密集模式实现加速。

  1. 在稀疏计算下，模型被转换为
    SMoE
    模型，相较于其原始形式，计算成本更低。稀疏激活使得
    SMoE
    模型能够模拟原始模型，从而在效率和效果之间取得平衡。
  2. 在密集计算期间，所有模型参数都被计算和优化，以实现更好的性能。

最终模型恢复为密集配置，以充分利用模型容量。此外，最终模型也适配稀疏计算，可以直接用于高效的稀疏推理，而无需任何额外的训练。

在密集计算中，前馈网络（
FFNs
）通过以下方式计算：

\[\begin{equation}
\small
\text{FFN}({\mathbf{x}}) = {\mathbf{W}}_o \sigma({\mathbf{W}}_i {\mathbf{x}} + {\mathbf{b}}_i) + {\mathbf{b}}_o,
\end{equation}
\]

在稀疏计算中，前馈网络（
FFNs
）被均分为
\(N\)
个专家，并以
SMoE
的方式进行计算，

\[\begin{equation}
\small
\text{FFN}_{\text{SMoE}}({\mathbf{x}}) = \sum_{n=1}^N \alpha_n {\mathbf{W}}_{o,n} \sigma({\mathbf{W}}_{i,n} {\mathbf{x}}),
\end{equation}
\]

使用门控网络来评估每个专家对于给定输入
\({\mathbf{x}}\)
的重要性，选择重要性分数最高的
\(K\)
个专家来计算输出。未被选择的专家的
\(\alpha_n\)
被设置为
\(0\)
。

密集转换为稀疏

  • 神经元聚类

使用平衡的
k-means
聚类将
\({\mathbf{W}}_i\)
的行（每一行代表一个特定神经元）聚类成
\(N\)
组，假定具有相似权重的神经元更可能被同时激活。

基于聚类结果
\({\mathbf{s}} \in \mathbb{R}^{d_{\text{ff}}}\)
，其中包含每个神经元的相应专家索引，将权重矩阵
\({\mathbf{W}}_i, {\mathbf{W}}_o\)
分割为
\(N\)
个子矩阵
\({\mathbf{W}}_{i,n}, {\mathbf{W}}_{o,n}\)
。

为了使转换更平滑，使用前一个
checkkpoint
的聚类中心作为当前
checkkpoint
聚类的初始化。这个简单的策略通常提供更好的结果，小于随机初始化中心的簇内平方和（
WCSS
）。

为了避免局部最优（特别是训练早期），进行两次聚类，一次使用随机初始化，另一次使用来自前一个
checkkpoint
的初始化，并选择更好的结果。形式上，第
\(j\)
次
checkkpoint
的聚类结果
\({\mathbf{s}}_j\)
由以下公式计算：

\[\begin{equation}
\small
{\mathbf{s}}_{j} = \min_{{\mathbf{s}} \in \{f({\mathbf{W}}_i), f({\mathbf{W}}_i, {\mathbf{s}}_{j-1})\}} \text{WCSS}({\mathbf{W}}_i, {\mathbf{s}}),
\end{equation}
\]

其中
\(f({\mathbf{W}}_i)\)
和
\(f({\mathbf{W}}_i, s_{j-1})\)
分别是使用随机初始化和来自前一个
checkkpoint
的初始化的聚类结果。

  • 专家选择

使用输入
\({\mathbf{x}}\)
与聚类中心之间的相似性作为重要性评分，以选择前
\(K\)
个专家。形式上，第
\(n\)
个专家的重要性评分由以下公式计算：

\[\begin{equation}
\small
\alpha_n = {\mathbf{x}}^\top {\mathbf{c}}_n,\quad{\mathbf{c}}_n = \frac{N}{d_{\text{ff}}} \sum_{m=1}^{\frac{d_{\text{ff}}}{N}} {\mathbf{W}}_{i,n}^m,
\end{equation}
\]

其中
\({\mathbf{W}}_{i,n}^m\)
是
\({\mathbf{W}}_{i,n}\)
的第
\(m\)
行，而
\({\mathbf{c}}_n\)
是第
\(n\)
个专家的聚类中心。

  • 转换时机

通过监控激活模式的变化以确定过渡时间，其中激活模式的相似性反映了激活模式的变化速率，当激活稀疏度较高且激活模式稳定时进行转换。

具体而言，设定一个阈值
\(\tau\)
，当两个连续
checkkpoint
之间的激活模式相似性大于
\(\tau\)
时切换到稀疏训练。

稀疏转换为密集

SMoE
模型的性能往往落后于具有相同参数的稠密模型，为了最优地利用模型容量并避免稀疏计算形式的过拟合，在训练期间战略性地多次回归到稠密训练。

当
\(K=N\)
时，
SMoE
计算与稠密计算是一致的，因此过渡到稠密计算是平滑的。通过连接所有专家的权重矩阵来进行此转换，从而获得稠密权重矩阵，同时忽略门控网络。

这个过渡使得全参数优化成为可能，有效缓解了稀疏训练引起的表示崩溃问题，并促进了激活模式的演变。

  • 转换时机

为了实现可控的速度比率，建议保持稀疏训练步骤与所有训练步骤之间的常数比率
\(r\)
。此外，为了确保最终模型可以进行稠密使用，在训练结束时采用稠密训练。

主要实验



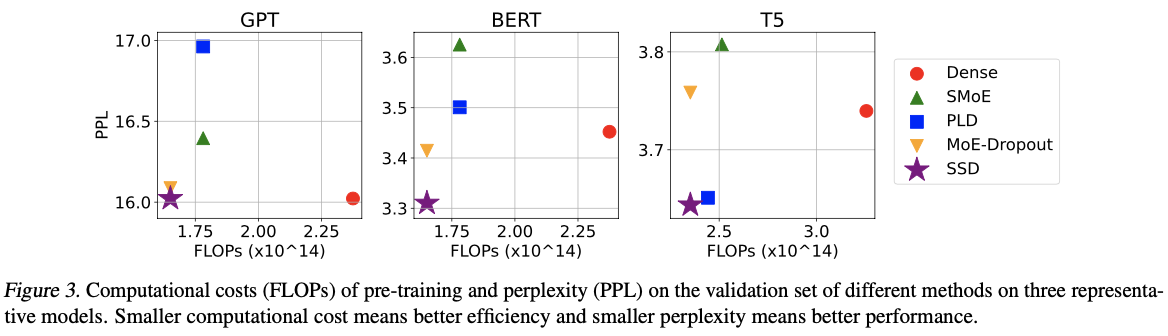
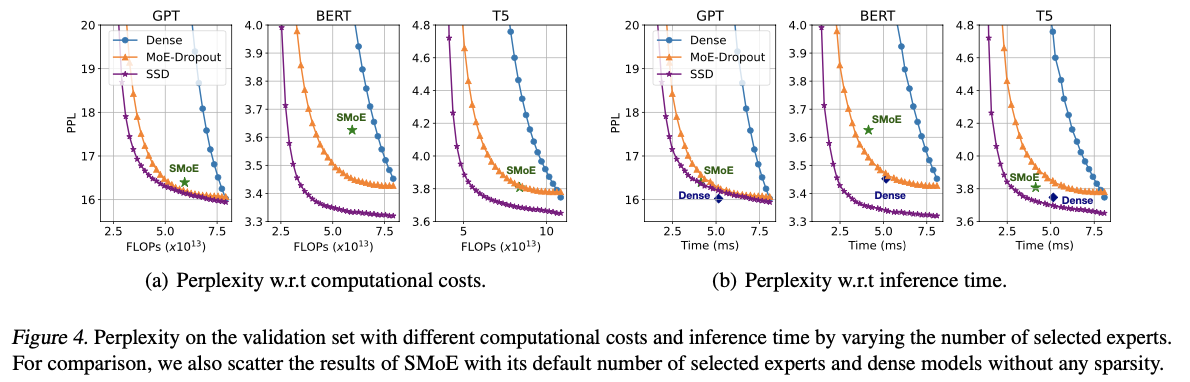
如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】

work-life balance.

标签: none

添加新评论