题目：请你来实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数。

01
、手动处理每个字符法

最简单的方法永远是脑海中第一个想到的方法，也是最暴力的方法，而这一题我们只需要安装题目要求一个一个字符处理即可，其实整个解法相当简单。

我们梳理一下解题思路，大致可分为以下三步：

（1）处理开头空格，通过while循环把开头的所有空格都去除掉；

（2）处理正负符号，判断是否包含+/-号，并做下标记；

（3）处理数字，首先判断当前字符是否为数值，如果是则计算出其值，并且检测是否溢出，在未溢出的情况下，通过x*10+digit的方式累计结果；

（4）最后根据正负号返回正确结果。

具体代码如下：

//解法 1：手动处理每个字符（经典解法）
public static int MyAtoi1(string s)
{
    //结果
    var result = 0;
    //当前处理字符索引
    var index = 0;
    //标记正负数
    var sign = 1;
    //字符串长度
    var length = s.Length;
    //去除开头的空格
    while (index < length && s[index] == ' ')
    {
        //处理下一个字符
        index++;
    }
    //处理正负符号
    if (index < length && (s[index] == '+' || s[index] == '-'))
    {
        //标记正负数
        sign = s[index] == '-' ? -1 : 1;
        //处理下一个字符
        index++;
    }
    //转换数字字符为数字
    while (index < length && char.IsDigit(s[index]))
    {
        //计算当前字符数值
        var digit = s[index] - '0';
        //检查是否溢出
        if (result > (int.MaxValue - digit) / 10)
        {
            return sign == 1 ? int.MaxValue : int.MinValue;
        }
        //累积当前字符至结果中
        result = result * 10 + digit;
        //处理下一个字符
        index++;
    }
    //返回结果
    return sign * result;
}

02
、正则表达式法

还有一种比较简洁的方式，可以直接通过正则表达式匹配出满足条件的字符，然后再通过BigInteger.TryParse进行类型转换，之所以选择BigInteger类型是因为其他值类型都可能导致溢出情况。

根据上一题的解题思路，我们来尝试一步一步用正则表达式实现。

首先需要匹配开头的空白字符。

^：表示一个锚点，匹配字符串的开头；

\s：表示特殊字符，匹配空白字符，包括空格、制表符、换行符等；

*：表示量词，表示其前面元素可以出现零次或多次；

因此可以通过^\s*来实现字符串开头的空格处理。

[]：定义一个字符类，表示匹配方括号中的任意一个字符；

+-：表示加号和减号，即正数和负数符号；

？：表示量词，表示其前面元素可以出现零次或一次；

因此可以通过[+-]?来实现匹配正负号。

\d：表示匹配一个数字字符，范围为0-9；

+：表示量词，表示其前面元素可以出现一次或多次；

因此可以通过\d+来实现连续数字字符匹配。

下面看看具体实现代码：

//解法 2：正则表达式法
public static int MyAtoi2(string s)
{
    //使用正则表达式匹配符合要求的部分
    //^\s*：表示匹配字符串开头的零个或多个空白字符（空格、制表符等）。
    //[+-]?：表示符号（+ 或 -）可选。
    //\d+：表示一个或多个数字。
    var match = System.Text.RegularExpressions.Regex.Match(s, @"^\s*[+-]?\d+");
    //匹配成功，并且可以转换为数值
    if (match.Success && BigInteger.TryParse(match.Value, out var result))
    {
        //大于int最大值
        if (result > int.MaxValue)
        {
            return int.MaxValue;
        }
        //小于int最小值
        if (result < int.MinValue)
        {
            return int.MinValue;
        }
        //返回结果
        return (int)result;
    }
    return 0;
}

03
、状态机法

此题还有一种经典解法，即状态机法，状态机的核心思想是在一组有限的状态中，并通过输入触发状态之间的转移。

我们以此题为例，假设在处理字符串的过程中，一直存在一个状态state，而每次处理的当前字符则可以触发当状态state转移到下一个状态state1，如此我们只需要枚举出所有state和当前字符关于state1的映射关系即可。

我们可以建立如下图所示状态机：

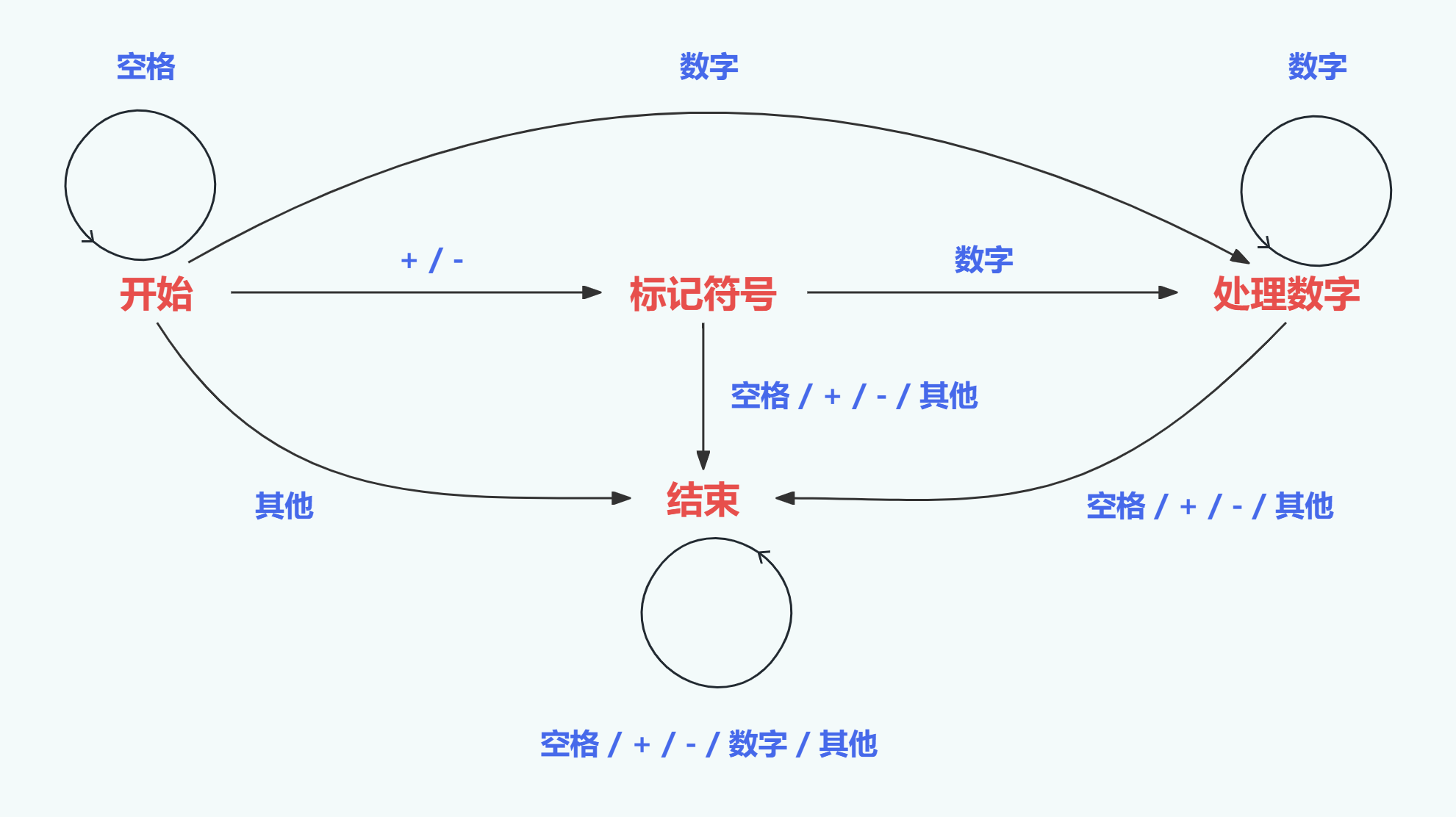
如上图，如果当前state为“开始”，并且当前字符为“空格”，则state1为“开始”，如果当前字符为“数字”，则state1为“处理数字”，以此类推，而state1则会绝对当前字符具体的处理方法。

我们也可以用以下表格来表示这个状态机：

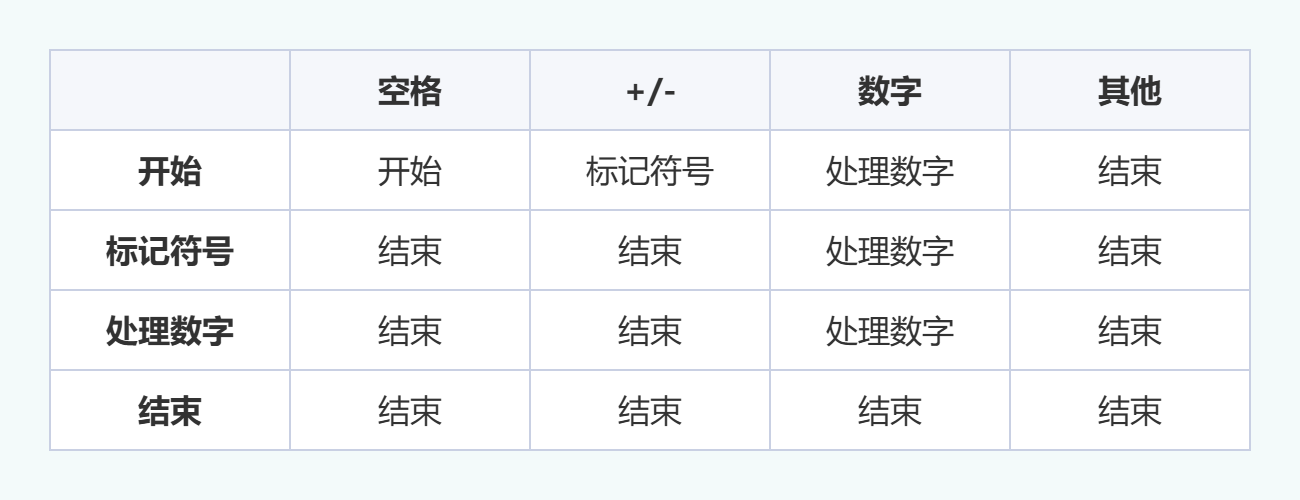
有了状态机状态关系映射表，我们就可以进行代码实现了，其逻辑也很简单，大致分为以下四步：

（1）构建状态机状态表；

（2）获取当前字符对应状态；

（3）通过状态转移确定当前字符处理逻辑；

（4）对要处理的字符串进行遍历处理得到最终结果；

具体实现代码如下：

//解法 3：状态机法
public int MyAtoi3(string s)
{
    Automaton automaton = new Automaton();
    return automaton.Atoi(s);
}
public class Automaton
{
    //0:"开始"状态
    private const int Start = 0;
    //1:"标记符号"状态
    private const int Signed = 1;
    //2:"处理数字"状态
    private const int InNumber = 2;
    //3:"结束"状态
    private const int End = 3;
    //符号:1为正数，0为负数
    private int _sign = 1;
    //数值结果
    private long _answer = 0;
    //记录当前处理状态
    private int _state = Start;
    //状态表
    private readonly Dictionary<int, int[]> _table = new Dictionary<int, int[]>()
    {
        {Start,new int[]{ Start, Signed, InNumber, End}},
        {Signed,new int[]{ End, End, InNumber, End}},
        {InNumber,new int[]{ End, End, InNumber, End}},
        {End,new int[]{ End, End, End, End}},
    };
    //处理当前字符
    private void Handle(char c)
    {
        //获取当前状态
        var currentState = GetState(c);
        //转移状态
        _state = _table[_state][currentState];
        switch (_state)
        {
            //处理数字
            case InNumber:
                _answer = _answer * 10 + c - '0';
                //溢出判断
                _answer = _sign == 1 ? Math.Min(_answer, int.MaxValue) : Math.Min(_answer, -(long)int.MinValue);
                break;
            //处理正负号
            case Signed:
                _sign = c == '+' ? 1 : -1;
                break;
            case Start:
            case End:
                break;
        }
    }
    //获取当前字符对应状态
    private static int GetState(char c)
    {
        //空格
        if (char.IsWhiteSpace(c))
        {
            return Start;
        }
        //正负号
        if (c == '+' || c == '-')
        {
            return Signed;
        }
        //数字
        if (char.IsDigit(c))
        {
            return InNumber;
        }
        //其他
        return End;
    }
    //字符串转换为整数
    public int Atoi(string s)
    {
        var length = s.Length;
        for (int i = 0; i < length; ++i)
        {
            Handle(s[i]);
        }
        return (int)(_sign * _answer);
    }
}

注
：测试方法代码以及示例源码都已经上传至代码库，有兴趣的可以看看。
https://gitee.com/hugogoos/Planner