强化学习算法中的log_det_jacobian —— 概率分布的仿射变换(Bijector)
相关:
https://colab.research.google.com/github/google/brax/blob/main/notebooks/training_torch.ipynb
之前写过一篇同主题的文章,后来发现这个文章中有一些问题,不过也有些不好改动,于是就新开一篇来进行更正和补充!!!
之前版本:
https://www.cnblogs.com/xyz/p/18564777
之所以之前版本有一些问题,其主要原因是其中的很多推理都是使用ChatGPT完成的,后来又遇到其他关于log_det_jacobian的算法,于是就重新遇到了相关问题,这时候通过查看相关资料发现ChatGPT的生成的理论推理有一些问题,但是出现的问题又十分不好察觉,于是就有了本篇。
要想知道log_det_jacobian是个什么东西,首先需要知道Bijector是什么。
A bijector is a function of a tensor and its utility is to transform one distribution to another distribution. Bijectors bring determinism to the randomness of a distribution where the distribution by itself is a source of stochasticity. For example, If you want a log density of distribution, we can start with a Gaussian distribution and do log transform using bijector functions. Why do we need such transformations, the real world is full of randomness and probabilistic machine learning establishes a formalism for reasoning under uncertainty. i.e A prediction that outputs a single variable is not sufficient but has to quantify the uncertainty to bring in model confidence. Then to sample complex random variables that get closer to the randomness of nature, we seek the help of bijective functions.
简单来说就是对一个分布进行变换,比如X服从高斯分布,y=tanh(x),那么Y服从什么分布呢,Y的概率密度如何计算,Y分布如何抽样,可以说Bijector就是指分布的变换,而log_det_jacobian就是在分布变换时计算概率密度所需要用到的。
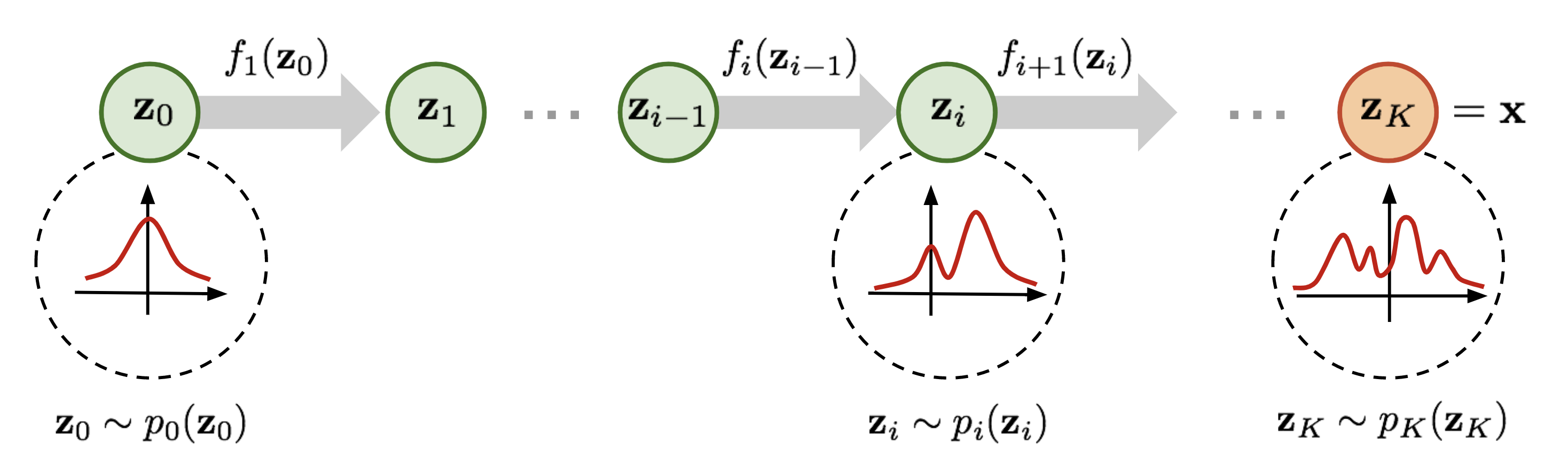
各个深度学习框架都针对机器学习中的这种概率分布变换的Bijector提供单独的计算方法,如:
paddle中的:
paddle.distribution.Transform
相关:
https://www.paddlepaddle.org.cn/documentation/docs/en/api/paddle/distribution/Transform_en.html


mindspore中的:
mindspore.nn.probability.distribution.TransformedDistribution
相关:

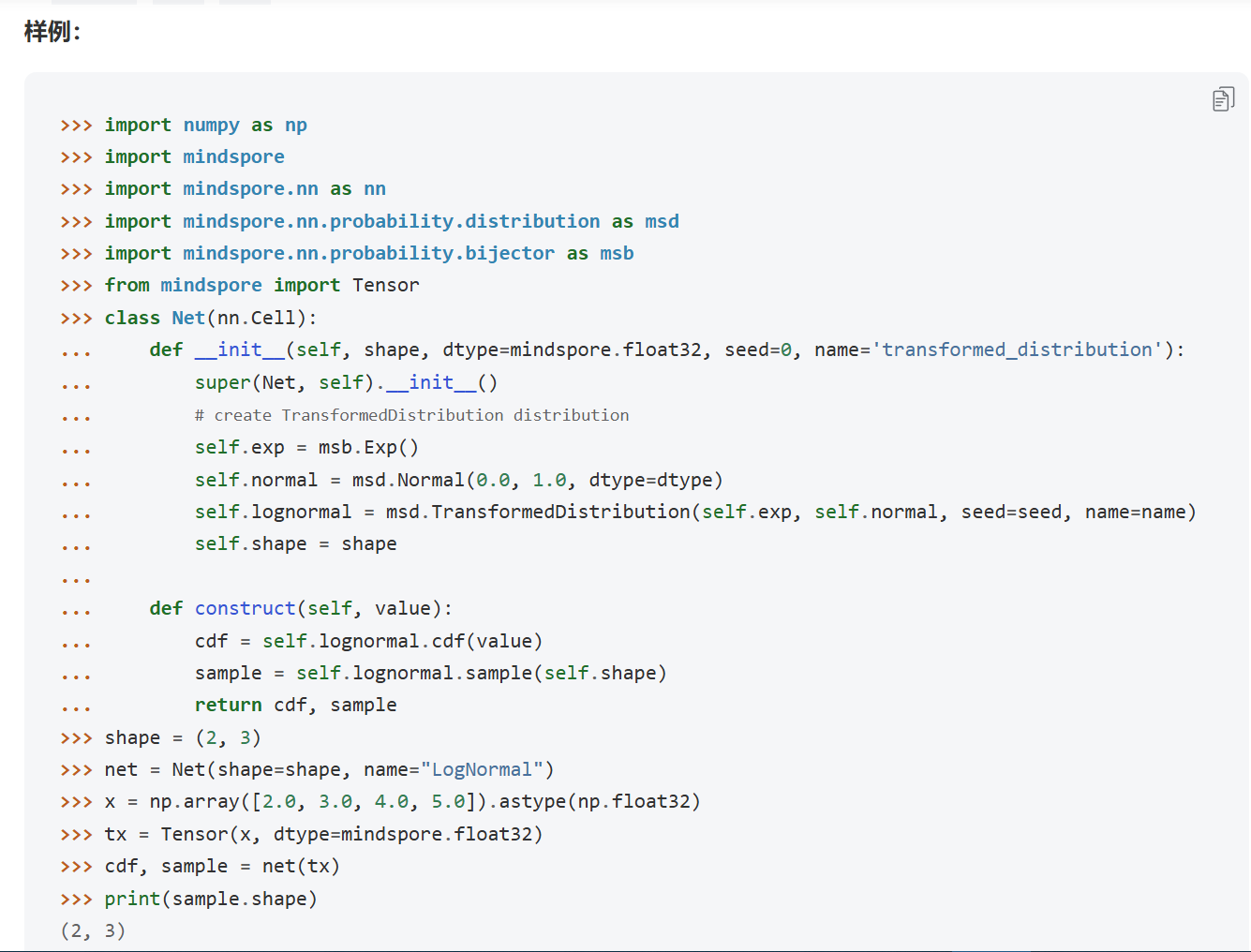
概率分布的仿射变换(Bijector)后的概率计算:
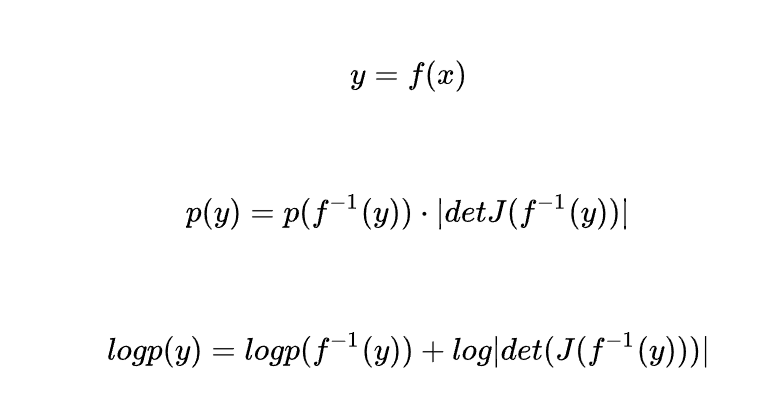
log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))
= log( tanh'(x) )
关于tanh函数的特性:

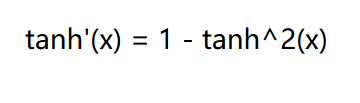
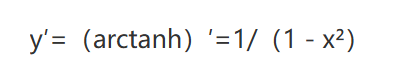
下图来自:
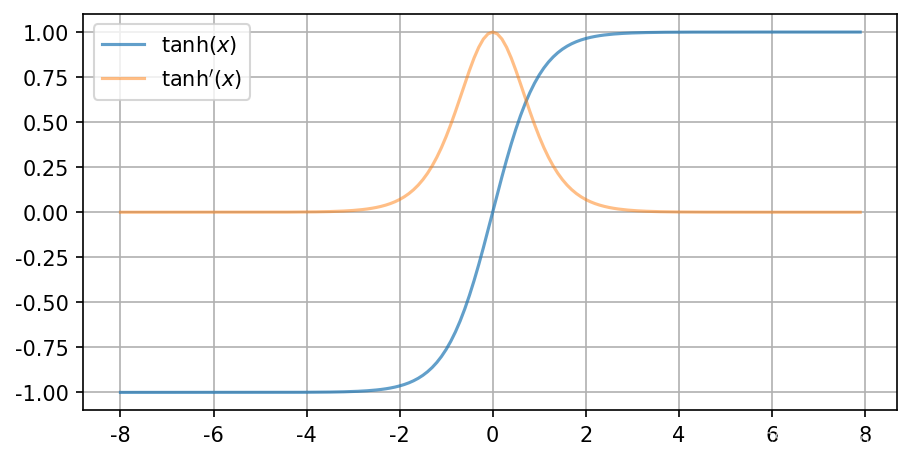
高斯函数的信息熵求解公式:

各个深度学习框架中的Probability模块的
不足之处
:
可以说在这个领域TensorFlow Probability (TFP)是最为功能强大和全面的,也是最为公认和广泛使用的,虽然我不喜欢用TensorFlow搞deep learning,但是必须要承认搞probability的深度学习的话还是用这个TensorFlow的TFP貌似更稳妥。
虽然Probability模块的可以自动实现分布变换后的概率密度,采样(sample),logP的计算,但是对于一些其他的计算其实支持并不是很好,如信息熵的计算,因为比如像信息熵这样的计算并不能由Probability模块自动获得,而是需要人为的设置,比如高斯分布的信息熵,这个就是需要人为手动的为不同的分布进行计算,因此可以说Probability模块并不能解决所有的分布变换后的新的统计量的计算,还是有一些需要手动推导计算公式并进行硬编码的,也或者是采用其他的近似的计算方法来解决。
相关: