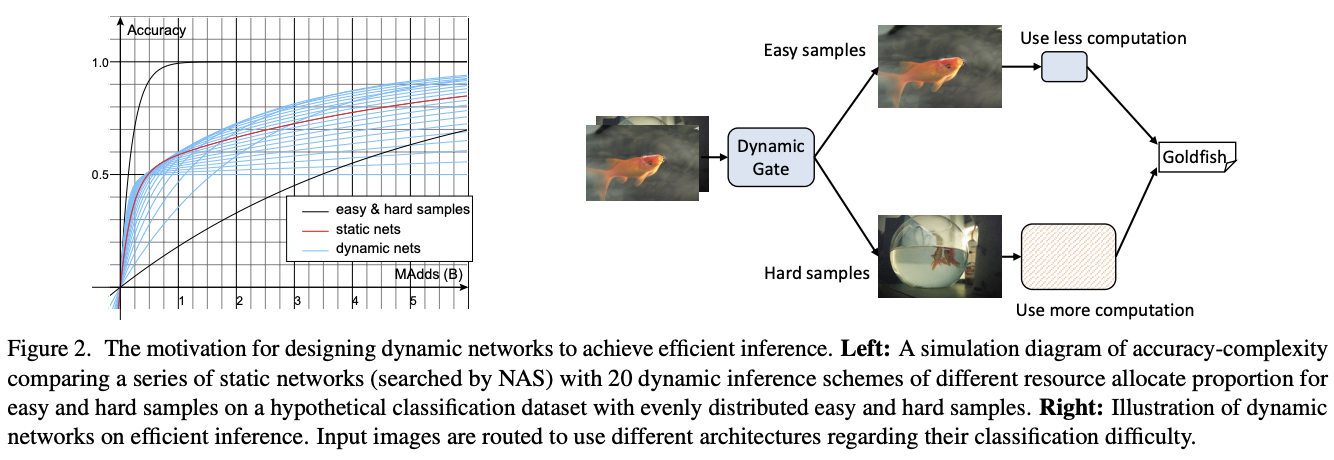
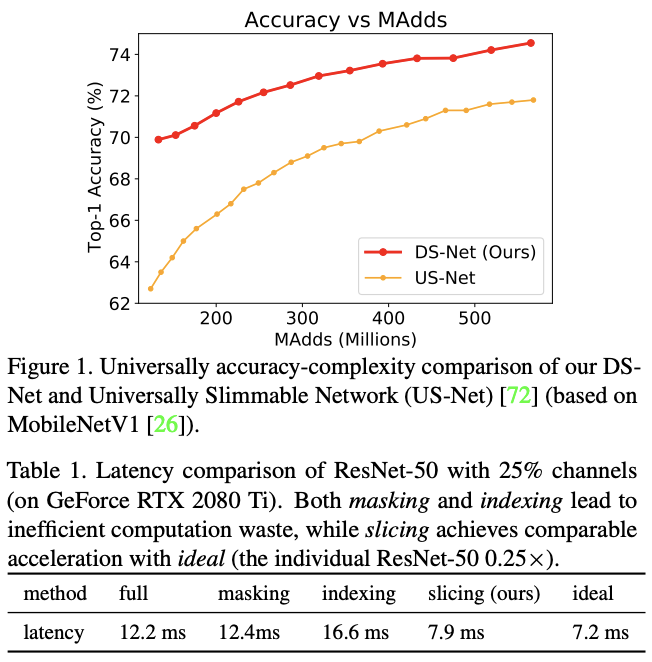
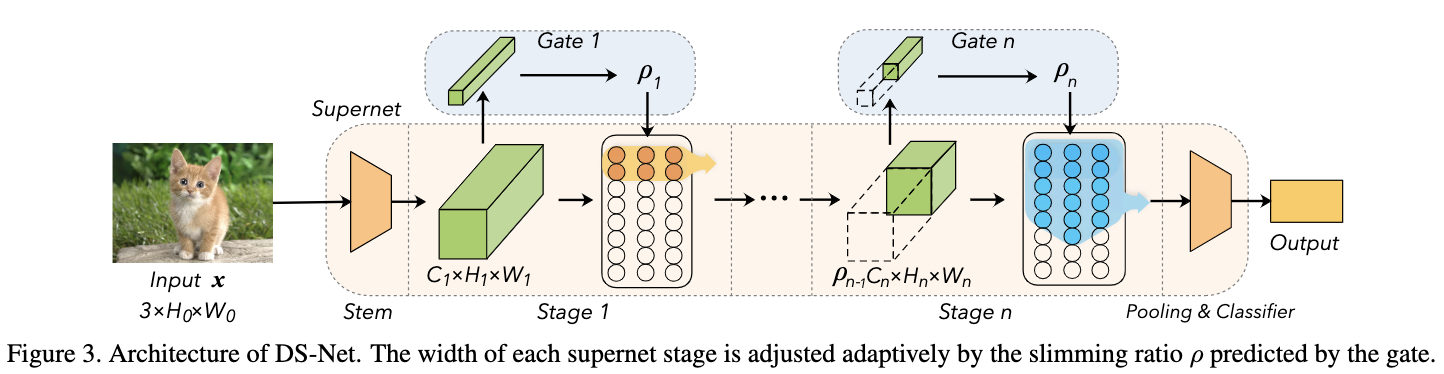
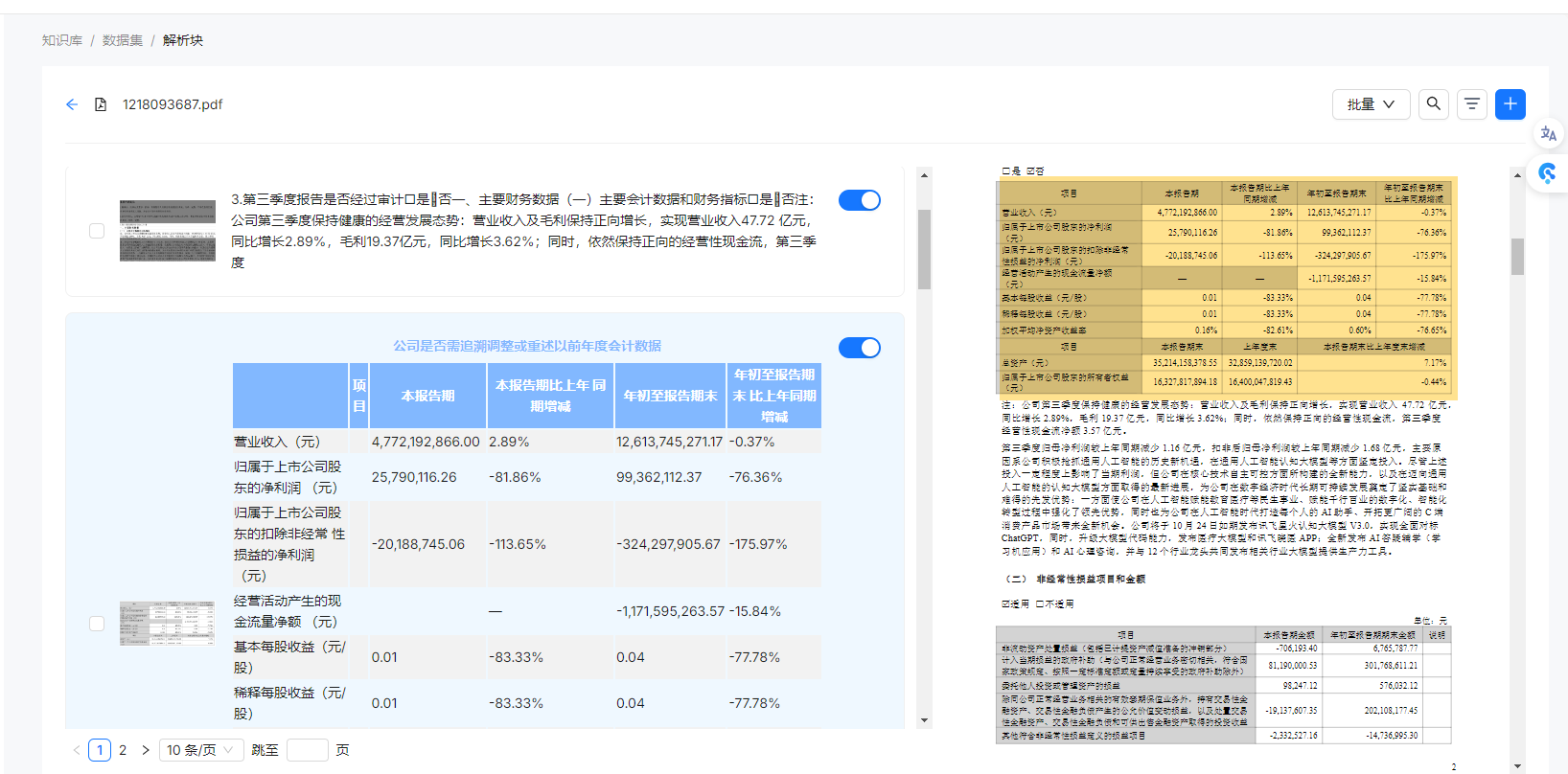
2. 支持向量机
对偶优化
拉格朗日乘数法可用于解决带条件优化问题,其基本形式为:
\[\begin{gather}
\min_w f(w),\\
\mathrm{s.t.} \quad \cases{g_i(w)\le 0,\\ h_i(w)=0.}
\end{gather}
\]
该问题的拉格朗日函数为
\[L(w,\alpha,\beta)=f(w)+\sum_{i}\alpha_ig_i(w)+\sum_j\beta_j h_j(w),
\]
定义
\[\begin{gather}
\mathcal{P}(w)=\max_{\alpha\ge 0,\beta} L(w,\alpha,\beta),\\
\mathcal{D}(\alpha,\beta)=\min_w L(w,\alpha,\beta),
\end{gather}
\]
容易看出,若
\(w\)
打破了原问题的某个限制条件,则
\(\mathcal P(w)=+\infty\)
,否则
\(\mathcal P(w)=f(w)\)
,因此原始问题可以表示为
\(\min_w\mathcal P(w)\)
;对应地,对偶问题可以表示为
\(\max_{\alpha\ge 0,\beta}\mathcal D(\alpha,\beta)\)
,也就是
\[\begin{gather}
\text{Primal: }\min_w\max_{\alpha\ge0,\beta} L(w,\alpha,\beta);\\
\text{Dual: }\max_{\alpha\ge 0,\beta}\min_w L(w,\alpha,\beta).
\end{gather}
\]
这就是原始问题对应的对偶问题,从上面可以得到原始问题与对偶问题最优解之间的关系:
\[d^*=\max_{\alpha\ge 0,\beta}\min_wL(w,\alpha,\beta)\le \min_w\max_{\alpha\ge 0,\beta}L(w,\alpha,\beta)=p^*.
\]
一般不能肯定原始问题与对偶问题具有相同的解,然而已有证明表明在一定条件下原始问题与对偶问题具有同一组解
\((w^*,\alpha^*,\beta^*)\)
,使得
\(p^*=d^*=L(w^*,\alpha^*,\beta^*)\)
,并且这组解满足KKT条件:
\[\begin{aligned}
\frac{\partial}{\partial w}L(w^*,\alpha^*,\beta^*)&=0;\\
\frac{\partial}{\partial\beta_j}L(w^*,\alpha^*,\beta^*)&=0,\quad \forall j;\\
\alpha_i^*g_i(w^*)&=0,\quad \forall i;\\
g_i(w^*)&\le 0,\quad \forall i;\\
\alpha_i^*&\ge 0,\quad \forall i.
\end{aligned}
\]
其中,第三条
\(\alpha_i^*g_i(w^*)=0\)
被称为互补松弛性.
支持向量机的优化目标
支持向量机的训练集
\(D=\{(x_i,y_i)\}\)
中,
\(y_i\in\{1,-1\}\)
,正例标签为
\(1\)
,负例标签为
\(-1\)
. 在几何直观上,支持向量机试图找到一个超平面
\(w'x+b=0\)
,使得所有样本在正确分类的前提下,所有点到超平面的直线距离的最小值最大.
- 由于
\(y_i\in\{1,-1\}\)
,故样本被正确分类意味着
\(y_i(w'x_i+b)>0\)
.
- 对任意点
\(x_i\)
,点到超平面
\(w'x+b=0\)
的距离为
\(d=\frac{|w'x_i+b|}{\|w\|}\)
.
- 支持向量机的目的是让所有样本被正确分类的同时,最大化所有点到超平面的最小距离.
综合以上三点,支持向量机意图找到一个
\(\gamma >0\)
作为所有点到超平面的最小距离,并最大化这个
\(\lambda\)
,因此支持向量机的初始优化问题是
\[\begin{gather}
\max\gamma >0,\\
\mathrm{s.t.}\quad \frac{y_i(w'x_i+b)}{\|w\|}\ge \gamma.
\end{gather}
\]
此时约束条件是非凸的,令
\(\gamma :=\frac{\gamma}{\|w\|}\)
,上述问题就转化成
\[\begin{gather}
\max \frac{\gamma}{\|w\|},\\
\mathrm{s.t.}\quad y_i(w'x_i+b)\ge \gamma.
\end{gather}
\]
此时目标函数是非凸的,然而
\((w,b)\)
作为超平面的参数可以进行伸缩变换,且问题的解
\((w,b,\gamma)\)
在目标函数和约束条件上均是齐次的,这就使得任意一组解
\((w,b,\gamma)\)
都可以等效为
\((\frac{w}{\gamma},\frac{b}{\gamma},1)\)
,即设定
\(\gamma\equiv1\)
不会影响解的存在,因此可以在问题的形式中隐去参数
\(\gamma\)
,最后将目标函数等效变换,就得到SVM原始问题:
\[\begin{gather}
\max\frac{1}{\|w\|}\iff\min \frac{1}{2}\|w\|^2,\\
\mathrm{s.t.}\quad y_i(w'x_i+b)\ge 1,\quad \forall i\in\{1,\cdots,n\}.
\end{gather}
\]
现在求其对偶问题. 此问题的拉格朗日函数是
\[L(w,b,\alpha)=\frac{1}{2}\|w\|^2+\sum_{i=1}^{n}\alpha_i(1-y_i(w'x_i+b)).
\]
对偶问题即
\(\max_{\alpha\ge 0}\min_{w,b} L(w,b,\alpha)\)
,要计算
\(\min_{w,b}L(w,b,\alpha)\)
需对
\(w,b\)
求偏导,并令偏导数等于
\(0\)
,即
\[\begin{aligned}
\frac{\partial L}{\partial w}=w-\sum_{i=1}^{n}\alpha_i y_ix_i=0&\implies w=\sum_{i=1}^{n}\alpha_iy_ix_i;\\
\frac{\partial L}{\partial b}=-\sum_{i=1}^{n}\alpha_iy_i=0&\implies \sum_{i=1}^{n}\alpha_iy_i=0.
\end{aligned}
\]
将
\(w=\sum_{i=1}^{n}\alpha_iy_ix_i\)
代回
\(L(w,b,\alpha)\)
,再结合
\(\sum_{i=1}^{n}\alpha_iy_i=0\)
以及
\(\alpha_i\ge 0\)
的条件,就得到对偶问题为
\[\begin{gather}
\max f(\alpha)= \sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j(x_i'x_j)\\
\mathrm{s.t.}\quad \cases{
\alpha_i\ge 0,\quad \forall i\ge 0,\\
\sum_{i=1}^{n}\alpha_iy_i=0.
}
\end{gather}
\]
线性不可分情形
线性不可分情形下,原始问题不可解,即不可能满足对所有样本都有
\(y_i(wx_i+b)\ge 1\)
,因此软间隔SVM对每个样本考虑一个容错
\(\xi_i\ge 0\)
,允许样本在一定程度上违背分类原则,但相应地在目标函数中施加惩罚,优化问题就产生如下变化:
\[\begin{gathered}
\min_{w,b} \frac{1}{2}\|w\|^2,\\
\mathrm{s.t.}\quad y_i(w'x_i+b)\ge 1.
\end{gathered}\implies
\begin{gathered}
\min_{w,b,\xi}\frac{1}{2}\|w\|^2+C\sum_{i=1}^{n}\xi_i,\\
\mathrm{s.t.}\quad \cases{y_i(w'x_i+b)\ge 1-\xi_i, \\
\xi_i\ge 0.}
\end{gathered}
\]
这里引入了超参数
\(C\)
表示对分类错误的容忍程度,
\(C\)
代表惩罚力度,
\(C=+\infty\)
时软间隔SVM就退化为硬间隔SVM. 同样求其对偶问题,拉格朗日函数是
\[L(w,b,\xi,\alpha,r)=\frac{1}{2}\|w\|^2+C\sum_{i=1}^{n}\xi_i-\sum_{i=1}^{n}\alpha_i(\xi_i+y_i(w'x_i+b)-1)-\sum_{i=1}^{n}r_i\xi_i,
\]
对偶问题是
\(\max_{\alpha\ge 0,r\ge 0}\min_{w,b,\xi}L(w,b,\xi,\alpha,r)\)
要求
\(\min_{w,b,\xi}(\alpha,r)\)
,就对
\(w,b,\xi\)
求偏导并令之等于
\(0\)
,得到
\[\begin{aligned}
\frac{\partial L}{\partial w}=w-\sum_{i=1}^{n}\alpha_iy_ix_i=0&\implies w=\sum_{i=1}^{n}\alpha_iy_ix_i,\\
\frac{\partial L}{\partial b}=-\sum_{i=1}^{n}\alpha_iy_i=0&\implies \sum_{i=1}^{n}\alpha_iy_i=0,\\
\frac{\partial L}{\partial \xi_i}=C-\alpha_i-r_i=0&\implies \alpha_i+r_i=C,\quad \forall i,
\end{aligned}
\]
将
\(w=\sum_{i=1}^{n}\alpha_iy_ix_i\)
代入到
\(L(w,b,\xi,\alpha,r)\)
中,并结合
\(\sum_{i=1}^{n}\alpha_iy_i=0\)
和
\(\alpha_i+r_i=C\)
的约束条件,就得到对偶问题
\[\begin{gather}
\max_{(\alpha,r)\ge 0}\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_jx_i'x_j,\\
\mathrm{s.t.}\quad \cases{\sum_{i=1}^{n}\alpha_iy_i=0,\\
\alpha_i\ge 0,\\
r_i\ge 0,\\
\alpha_i+r_i=C}\implies \cases{\sum_{i=1}^{n}\alpha_iy_i=0,\\
0\le \alpha_i\le C.}
\end{gather}
\]
可以看到,软间隔SVM相比硬间隔SVM,它们的对偶问题优化目标一致,唯一区别在于为每一个
\(\alpha_i\)
添加了上界
\(C\)
,因此仅在求解时有些许区别.
原始问题与对偶问题的关联
现在根据原始问题推导得到对偶问题,并且假定已经了解对偶问题的解法. 然而最终回到问题本身,还是要找到对应的分组超平面
\((w,b):w'x+b=0\)
,因此需要了解原始问题与对偶问题的关联.
首先,讨论的前提是原始问题与对偶问题同解,对支持向量机而言,已有证明表明这一条件是成立的,即原始问题与对偶问题共享拉格朗日函数的一组解,记作
\((w^*,b^*,\alpha^*[,\xi^*,r^*])\)
(中括号内是软间隔SVM独有的变量),且KKT条件也成立,这意味着互补松弛性
\(\alpha_i^*g_i(w^*)=0\)
对任何样本
\(i\)
都成立.
在上述前提下,考虑下面的几个问题:
- 互补松弛性
\(\alpha_i^*g_i(w^*)=0\)
意味着什么?
- 求得对偶问题的解
\(\alpha^*\)
后如何回推分类超平面
\((w^*,b^*)\)
?
- 如何利用优化后的支持向量机
\((w^*,b^*,\alpha^*)\)
判别样本点?
首先,第一个问题中,互补松弛性成立表明对每个样本
\(i\)
,都有
\(\alpha_i^*g_i(w^*)=0\)
,回到问题定义上,
\(\alpha_i\ge 0\)
是对偶问题中约束条件
\(g_i(w^*)\le 0\)
即
\(y_i(w_ix+b)\ge 1-\xi_i\)
的对应系数,既然
\(\alpha_i\ge 0\)
且
\(g_i(w^*)\le 0\)
,那么要使
\(\alpha_i^*g_i(w^*)=0\)
,就必须满足
\(\alpha_i^*=0\)
或
\(g_i(w^*)=0\)
. 而
\(\alpha\)
是通过对偶问题求解直接获得的,并且与每个样本对应,因此对每个样本,必定满足下面两个条件中的至少一个(硬间隔SVM中不含
\(\xi_i\)
):
- \(\alpha_i^*=0\)
,此时
\(y_i(w'x_i+b)> 1-\xi_i\)
,这样的样本称为非支持向量,它经过
\(\xi_i\)
调节后落在分隔超平面的间隔外.
- \(\alpha_i^*>0\)
,此时
\(y_i(w'x_i+b)=1-\xi_i\)
,这样的样本称为支持向量,它经过
\(\xi_i\)
调节后落在分隔超平面的间隔上.
实际数据集中,非支持向量的数量总是远多于支持向量,即大多数样本总是落在分隔超平面以外,支持向量的数量相对较少,但只有它们对分类器产生实质影响,因此分类器才被称为支持向量机. 为什么说只有支持向量会实质上地影响分类器,要看第二个问题与第三个问题,下面用
\(SV\)
表示支持向量(support vector)所构成的集合.
第二个问题,即如何根据
\(\alpha^*\)
反推
\((w^*,b^*)\)
,这由优化过程中的偏导条件可得. 注意到令
\(\frac{\partial L}{\partial w}=0\)
时得到了
\(w=\sum_{i=1}^{n}\alpha_iy_ix_i\)
,这正是最优解所满足的条件,即
\[w^*=\sum_{i=1}^{n}\alpha_i^*y_ix_i,
\]
进一步地,因为当且仅当样本为支持向量时
\(\alpha_i^*>0\)
,即对大多数样本有
\(\alpha_i^*=0\)
,这部分样本对
\(w^*\)
没有贡献,也就是
\[w^*=\sum_{i\in SV}\alpha_i^*y_ix_i.
\]
接下来考虑
\(b^*\)
,同样根据互补松弛性,当且仅当样本为支持向量时成立
\(y_i(w'x_i+b^*)=1-\xi_i\)
,因此对每个支持向量,如果能求得
\(\xi_i\)
的值就能得到
\(b^*\)
的值. 注意到当
\(\alpha_i<C\)
时
\(r_i>0\)
,从而
\(\xi_i=0\)
,因此只要能够找到一个
\(\alpha_i\in (0,C)\)
,就能通过计算得到
\(b^*=y_i-(w^*)'x_i\)
(注意到
\(\frac{1}{y_i}=y_i\)
). 往往可以对所有这样的样本做一个平均以平滑,即
\[b^*=\frac{1}{|\{i:0<\alpha_i<C\}|}\sum_{i:0<\alpha_i<C}\left(y_i-\sum_{j\in SV}\alpha_j^*y_jx_j'x_i \right),
\]
特别对硬间隔支持向量机,此时在正负样本中都必定存在一个支持向量,落在超平面间隔上,从而
\[\begin{gather}
\min_{i:y_i=1}w'x_i+b^*=1,\\
\max_{i:y_i=-1}w'x_i+b^*=-1,\\
b^*=-\frac{\min_{i:y_i=1}(w'x_i)+\max_{i:y_i=-1}(w'x_i)}{2}.
\end{gather}
\]
最后一个问题即如何判别样本,这个问题相对简单,因为训练集中正样本总满足
\((w^*)'x_i+b^*\ge 1\)
,负样本总满足
\((w^*)'x_i+b^*\le -1\)
,
\(\xi_i\)
是针对特殊情况的补偿,因此在模型使用时不需考虑,未知样本
\(x_0\)
的分类就是
\[\hat{y}_0=\mathrm{sign}\left((w^*)'x_0+b^* \right)=\mathrm{sign}\left(\sum_{i\in SV}\alpha_i^*y_ix_i'x_0+b^* \right).
\]
可以看到,求解完毕的支持向量机中,无论是参数表示还是模型使用,均只与支持向量有关.
核技巧
线性不可分时,除了能使用软间隔SVM以外,还可以用特征映射
\(\varphi(\cdot)\)
将样本
\((x_i,y_i)\)
映射到高维
\((\varphi(x_i),y_i)\)
,因为高维空间中的数据更系数,线性可分的可能性也更大. 然而,
\(\varphi(\cdot)\)
往往是形式未知、维度极高甚至是无限维的,在这种情形下,核技巧(kernel trick)提供了一种绕开
\(\varphi(\cdot)\)
的计算,不显式地计算转化后的数据集
\(\varphi(x_i)\)
,也能在转化后的高维空间中使用支持向量机的方法.
先回顾支持向量机应用于非特征映射数据集时的步骤:
- 构建对偶问题求解,在
\(\sum_{i=1}^{n}\alpha_iy_i=0\)
且
\(\alpha_i\in[0,C]\)
的情况下求解
\(\max_{\alpha}\left(\sum_{i}\alpha_i-\frac{1}{2}\sum_{i,j}\alpha_i\alpha_jy_iy_j(x_i'x_j) \right)\)
.1.
- 得到最优解
\(\alpha\)
后,找到一个
\(\alpha_k\in (0,C)\)
,反推
\(b=y_k-\sum_{i}\alpha_iy_i(x_i'x_k)\)
.
- 得到分割超平面
\(\sum_i\alpha_iy_i(x_i'x)+b=0\)
,判别新样本
\(y_0=\mathrm{sign}(\sum_{i}\alpha_iy_i(x_i'x_0)+b)\)
.
注意到上面的过程中,有意地隐去了
\(w\)
的计算,因为不论在模型表示还是样本归类中,都不需要显式地得到
\(w\)
的具体值;并且,任何出现了样本特征
\(x\)
的地方,总是以内积
\(x_i'x_j\)
的形式出现. 这说明,即使使用了特征映射
\(\varphi(\cdot)\)
,也不必显式地得到每个样本
\(x\)
对应的高维特征
\(\varphi(x)\)
,但是对任意样本对
\((x_i,x_j)\)
,它们的内积
\(\varphi(x_i)'\varphi(x_j)\)
却是必要的.
因此,核技巧不显式地求解
\(\varphi(\cdot)\)
,而是用一个对称二元函数
\(\kappa:(\mathbb{R}^{d},\mathbb{R}^{d})\mapsto \mathbb{R}\)
定义了内积:
\(\kappa(x_i,x_j)=\varphi(x_i)'\varphi(x_j):=\langle x_i,x_j\rangle\)
,这样,将核技巧运用于支持向量机就可以将上面的步骤直接改写为:
- 构建对偶问题求解,在
\(\sum_{i=1}^{n}\alpha_iy_i=0\)
且
\(\alpha_i\in[0,C]\)
的情况下求解
\(\max_{\alpha}\left(\sum_{i}\alpha_i-\frac{1}{2}\sum_{i,j}\alpha_i\alpha_jy_iy_j\langle x_i,x_j\rangle \right)\)
.
- 得到最优解
\(\alpha\)
后,找到一个
\(\alpha_k\in (0,C)\)
,反推
\(b=y_k-\sum_{i}\alpha_iy_i\langle x_i,x_k\rangle\)
.
- 得到分割超平面
\(\sum_i\alpha_iy_i\langle x_i,x\rangle+b=0\)
,判别新样本
\(y_0=\mathrm{sign}(\sum_{i}\alpha_iy_i\langle x_i,x_0\rangle+b)\)
.
综上所述,核技巧就是在不使用特征映射
\(\varphi(\cdot)\)
的显式表达的同时,利用内积完成了特征映射所需要达到的目标,使得用户不需要考虑如何变换样本的特征,只需尝试不同的核函数即可. 常用的核函数有:
- 线性核:
\(\kappa( x_i, x_j)= x_i' x_j\)
.
- 多项式核:
\(\kappa( x_i, x_j)=( x_i' x_j)^{d}\)
.
- 高斯核:
\(\kappa( x_i, x_j)=\exp(-\frac{\| x_i- x_j\|^2}{2\sigma^2})\)
.
- 拉普拉斯核:
\(\kappa( x_i, x_j)=\exp(-\frac{\| x_i- x_j\|}{\sigma})\)
.
- Sigmoid核:
\(\kappa( x_i, x_j)=\tanh(\beta x_i' x_j+\theta)\)
.
甚至核函数的形式也不是必要的,只要有办法得到每一个样本对的核函数值即可,因此在训练过程中,传入一个核矩阵
\(K\in\mathbb{R}^{n\times n}\)
代表样本对的核函数值,并在使用过程中传入样本
\(x_0\)
的同时,传入一个向量
\(k_0\in\mathbb{R}^{n}\)
代表
\(x_0\)
与所有训练样本的核函数值,就可以等效地作为核函数使用.
不过,由于核函数本身是特征映射内积的替代,所以核函数本身需要满足一定的条件. Mercer表明任何半正定函数都可以作为核函数使用,半正定函数指的是对任意数据集
\((x_1,\cdots,x_n)\)
,核函数
\(\kappa\)
诱导的矩阵
\(K\in\mathbb{R}^{n\times n}:K_{ij}=\kappa(x_i,x_j)\)
都是对称半正定的. 即使传入核矩阵
\(K\)
代替核函数,那么
\(K\)
本身也要是对称半正定矩阵,并且加入训练样本后,它与其他样本构成的核向量也要在增广意义下是对称半正定的.
SMO算法
最后进入到求解对偶问题的算法,常使用SMO(序列最小优化)算法对SVM的对偶问题进行求解,其思想是在对偶问题的
\(n\)
个变量中每次只选择两个进行优化,通过约束
\(\sum_{i=1}^{n}\alpha_iy_i=0\)
,固定
\(n-2\)
个变量使得每次优化只有一个
\(\alpha_i\)
可以自由变化,因此可以通过求梯度的方式直接优化.
对软间隔SVM,令
\(K_{ij}=\langle x_i,x_j\rangle\)
即
\(x_i,x_j\)
的核函数值,目标是最大化
\[\max_{\alpha}\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i,j}\alpha_i\alpha_jy_iy_jK_{ij},
\]
现选择变量对
\((\alpha_1,\alpha_2)\)
优化并将其他变量用无关值
\(C\)
代替,那么约束变为
\(\alpha_1y_1+\alpha_2y_2=\zeta\)
,目标就变成
\[\begin{aligned}
&\quad \max_{\alpha_1,\alpha_2} W(\alpha_1,\alpha_2)\\&=\alpha_1+\alpha_2-\frac{1}{2}\left(\alpha_1^2K_{11}+\alpha_2^2K_{22}+2\alpha_1\alpha_2y_1y_2K_{12}\right)\\
&\quad -\left(\alpha_1y_1\sum_{j=3}^{n}\alpha_jy_jK_{1j}+\alpha_2y_2\sum_{j=3}^{n}\alpha_jy_jK_{2j}\right)+C.
\end{aligned}
\]
再将约束条件:
\(\alpha_2=\zeta y_2-\alpha_1y_1y_2\)
代入,并令
\(\sum_{j=3}^{n}\alpha_jy_jK_{ij}=v_i(i=1,2)\)
,就得到关于
\(\alpha_1\)
的一元二次优化问题
\[\begin{aligned}
&\quad W(\alpha_1)\\
&=-\frac{1}{2}\left(\alpha_1^2K_{11}+(\zeta y_2-\alpha_1y_1y_2)^2K_{22}+2\alpha_1(\zeta y_2-\alpha_1y_1y_2)y_1y_2K_{12} \right)\\
&\quad +\alpha_1+\zeta y_2-\alpha_1(y_1y_2)-\alpha_1y_1v_1-(\zeta y_2-\alpha_1y_1y_2)y_2v_2+C\\
&=-\frac{1}{2}\left(\alpha_1^2K_{11}+\alpha_1^2K_{22}+\zeta^2K_{22}-2\alpha_1\zeta y_1K_{22}+2\zeta y_1\alpha_1K_{12}-2\alpha_1^2K_{12} \right)\\
&\quad +\alpha_1+\zeta y_2-\alpha_1(y_1y_2)-\alpha_1y_1v_1-\zeta v_2+\alpha_1y_1v_2+C\\
&=\left(K_{12}-\frac{1}{2}K_{11}-\frac{1}{2}K_{22} \right)\alpha_1^2\\
&\quad +\left(\zeta y_1K_{22}-\zeta y_1K_{12}+1-y_1y_2-y_1v_1+y_1v_2 \right)\alpha_1\\
&\quad +C+\zeta y_2-\zeta v_2-\frac{1}{2}\zeta^2K_{22}.
\end{aligned}
\]
令
\(\frac{\partial W(\alpha_1)}{\partial \alpha_1}=0\)
就得到
\(\alpha_1\)
应满足的条件为
\[\alpha_1(K_{11}+K_{12}-2K_{12})=y_1(\zeta K_{12}-\zeta K_{22}+y_1-y_2-v_1+v_2),
\]
在求得
\(\zeta\)
、
\(v_1\)
和
\(v_2\)
的同时,已经可以计算得到
\(\alpha_1\)
、
\(\alpha_2\)
的值. 注意,在软间隔SVM中还需要满足
\(\alpha_1\in[0,C]\)
与
\(\alpha_2\in[0,C]\)
,并结合约束
\(\alpha_1y_1+\alpha_2y_2=\zeta\)
. 这里分两种情况:
- \(y_1\ne y_2\)
时,约束变为
\(\alpha_1-\alpha_2=k\)
,其中
\(k\)
的正负性未知,因此
\(\max(0,k)\le\alpha_1\le\min(C,C+k)\)
.
- \(y_1=y_2\)
时,约束变为
\(\alpha_1+\alpha_2=k\)
,其中
\(k\)
与
\(C\)
的大小关系未知,因此
\(\max(0,k-C)\le\alpha_1\le \min(C,k)\)
.
- 对
\(k\)
的求值,注意到参数更新前后始终有
\(\alpha_1y_1+\alpha_2y_2=\zeta\)
且
\((y_1,y_2)\)
不变,因此可以直接用更新前的参数计算
\(k\)
.
- 得到的上下界同时适用于
\(\alpha_1\)
和
\(\alpha_2\)
,若求得的
\(\alpha_1,\alpha_2\)
超出此边界,则进行矩形修剪.
上述形式还可以继续化简,注意对
\(\alpha^\text{new}\)
和
\(\alpha^\text{old}\)
作区分. SVM对样本
\(x\)
的预测为
\(f(x)=\sum_{i=1}^{n}\alpha_i^\text{old}y_i\langle x_i,x\rangle +b\)
,因此
\[\begin{aligned}
v_1&=f(x_1)-\alpha_1^\text{old}y_1K_{11}-\alpha_2^\text{old}y_2K_{12}-b,\\
v_2&=f(x_2)-\alpha_1^\text{old}y_1K_{12}-\alpha_2^\text{old}y_2K_{22}-b,\\
v_1-v_2&=f(x_1)-f(x_2)-\alpha_1^\text{old}y_1(K_{11}-K_{12})-\alpha_2^\text{old}y_2(K_{12}-K_{22}),
\end{aligned}
\]
再将
\(\alpha_2=\zeta y_2-\alpha_1y_1y_2\)
代入(此式子对
\(\alpha^\text{new}\)
和
\(\alpha^\text{old}\)
均成立),就得到
\[\begin{aligned}
v_1-v_2&=f(x_1)-f(x_2)-\alpha_1^\text{old}y_1(K_{11}-K_{12})-(\zeta -\alpha_1^\text{old} y_1)(K_{12}-K_{22})\\
&=f(x_1)-f(x_2)-\alpha_1^\text{old}y_1(K_{11}+ K_{22}-2K_{12})-\zeta(K_{12}-K_{22})
\end{aligned}
\]
将其带回
\(\frac{\partial W(\alpha_1)}{\partial \alpha_1}\)
得到
\[\begin{aligned}
&\quad \alpha_1^\text{new}(K_{11}+K_{12}-2K_{12})\\
&=y_1(y_1-y_2-(f(x_1)-f(x_2)-\alpha_1^\text{old}y_1(K_{11}+K_{12}-2K_{12})))\\
&=y_1\left(y_1-f(x_1)-(y_2-f(x_2)) \right)+\alpha_1^\text{old}(K_{11}+K_{12}-2K_{12}),
\end{aligned}
\]
令
\(E_i=f(x_i)-y_i\)
为旧模型在第
\(i\)
个样本上的预测误差,就有
\[\alpha_1^\text{new}=\alpha_1^\text{old}-\frac{y_1(E_1-E_2)}{K_{11}+K_{12}-2K_{12}},
\]
上式略过了一些繁琐参数(如
\(C\)
、
\(\zeta\)
)的计算,形式美观,但应用上依赖于旧模型
\(f(\cdot)\)
,这意味着每次更新参数后需要得到新的模型,即需要对
\(b\)
进行更新. 注意到,至少有一个
\(\alpha_i\)
不在边界
\([0,C]\)
上时
\(x_i\)
是支持向量,此时有
\[y_i\sum_{j=1}^{n}\alpha_j^\text{new}y_j\langle x_j,x_i\rangle+b^\text{new}=1\implies b^\text{new}=1-y_i\sum_{j=1}^{n}\alpha_j^\text{new} y_i\langle x_j,x_i\rangle.
\]
若两个
\(\alpha_i\)
经更新后均不在边界上,则通过两个
\(x_i\)
计算得到的
\(b^\text{new}\)
相等;若两个
\(\alpha_i\)
经更新后均在边界上,则取用这两个样本计算得到的
\(b\)
的中点作为
\(b^\text{new}\)
.
综上,给出SMO算法更新软间隔SVM的含代数步骤:
- 随机选择一对样本对应的变量作为更新变量
\((\alpha_i,\alpha_j)\)
.
- 令
\(E_k=f(x_k)-y_k\)
为旧SVM的预测误差,计算无修剪的更新值
\(\alpha_i^\text{new}=\alpha_i^\text{old}-\frac{y_i(E_i-E_j)}{K_{ii}+K_{jj}-2K_{ij}}\)
.
- 求
\(\alpha_i^\text{new}\)
的修剪上下限:若
\(y_i\ne y_j\)
则约束为
\(\alpha_i-\alpha_j=k\)
,因此
\(L=\max(0,\alpha_i^\text{old}-\alpha_j^\text{old})\)
,
\(H=\min(C,C+\alpha_i^\text{old}-\alpha_j^\text{old})\)
;若
\(y_i=y_j\)
则约束为
\(\alpha_i+\alpha_j=k\)
,因此
\(L=\max(0,\alpha_i^\text{old}+\alpha_j^\text{old}-C)\)
,
\(H=\min(C,\alpha_i^\text{old}+\alpha_j^\text{old})\)
.
- 修剪解:将
\(\alpha_i^\text{new}\)
修剪至
\([L,H]\)
之间,并根据
\(\alpha_i^\text{old}y_i+\alpha_j^\text{old}y_j=\alpha_i^\text{new}y_i+\alpha_j^\text{new}y_j\)
得到
\(\alpha_j^\text{new}\)
.
- 更新
\(b\)
:若
\(\alpha_i^\text{new}\)
和
\(\alpha_j^\text{new}\)
中至少有一个是支持向量(设为
\(i\)
),则更新
\(b^\text{new}=1-y_i\sum_{j}\alpha_j^\text{new}y_jK_{ji}\)
;若二者均不是支持向量,则依然用此法计算两个
\(b\)
,取它们的平均作为
\(b^\text{new}\)
.
- 循环上述步骤,取不同的更新变量对进行更新.
SVM分类的建议代码实现
下面给出了使用SMO算法训练SVM分类器的具体实现,这里使用了随机抽选的方式选择每次更新的变量对
\((\alpha_i,\alpha_j)\)
,并且使用内积核函数,指定
\(C=+\infty\)
代表一个硬间隔分类器. 模型对一个人造数据集合真实数据集
breast_cancer
都有较为不错的分辨能力,需注意要对模型标签进行
\(\{-1,1\}\)
化,同时这里还对特征进行归一化以防止数值溢出.
import numpy as np
from sklearn.datasets import load_breast_cancer
class SVM:
def __init__(self, X, y, kernel=None):
self.X = np.array(X)
self.y = np.array(y) # {-1, 1}
if not kernel:
kernel = np.dot
self.kernel = kernel
self.n_samples, self.dim = self.X.shape
self.alpha = np.zeros(self.n_samples)
self.b = 0
def fit(self, max_iter=10000, C=float('inf')):
for k in range(max_iter):
i, j = np.random.choice(self.n_samples, 2, replace=False)
Ei = self.predict(self.X[i]) - self.y[i]
Ej = self.predict(self.X[j]) - self.y[j]
eta = self.kernel(self.X[i], self.X[i]) + self.kernel(self.X[j], self.X[j]) - 2 * self.kernel(self.X[i], self.X[j])
alpha_i_unclipped = self.alpha[i] - self.y[i] * (Ei-Ej) / eta
alpha_i_clipped, alpha_j_clipped = 0, 0
if self.y[i] == self.y[j]:
K_constant = self.alpha[i] + self.alpha[j]
lower_bound = max(0, K_constant - C)
upper_bound = min(C, K_constant)
alpha_i_clipped = self.__clip(alpha_i_unclipped, lower_bound, upper_bound)
alpha_j_clipped = K_constant - alpha_i_clipped
else:
K_constant = self.alpha[i] - self.alpha[j]
lower_bound = max(0, K_constant)
upper_bound = min(C, C + K_constant)
alpha_i_clipped = self.__clip(alpha_i_unclipped, lower_bound, upper_bound)
alpha_j_clipped = alpha_i_clipped - K_constant
self.alpha[i], self.alpha[j] = alpha_i_clipped, alpha_j_clipped
if self.alpha[i] > 0 and self.alpha[i] < C:
self.b = self.__calculate_b(i)
elif self.alpha[j] > 0 and self.alpha[j] < C:
self.b = self.__calculate_b(j)
else:
self.b = (self.__calculate_b(i) + self.__calculate_b(j)) / 2.0
def __clip(self, alpha, L, H):
if alpha < L:
return L
elif alpha > H:
return H
else:
return alpha
def __calculate_b(self, ind):
return 1 - self.y[ind] * np.dot(self.y * self.alpha, self.kernel(self.X, self.X[ind]))
def predict(self, x):
x = np.array(x)
if len(x.shape) == 1:
return self.b + np.sum(self.alpha * self.y * self.kernel(self.X, x))
elif len(x.shape) == 2:
return self.b + np.dot(self.alpha * self.y, self.kernel(self.X, x.T))
def predict_label(self, x):
y_pred = self.predict(x)
return np.sign(y_pred)
def acc(pred, label):
return (pred == label).mean()
np.random.seed(0)
d = 5; n = 200
X_syn = [np.random.multivariate_normal(mean=np.random.normal(size=d), cov=np.identity(d) / 5, size=(100,)) for i in range(2)]
X_syn = np.vstack(X_syn)
y_syn = np.repeat([-1, 1], 100)
clf = SVM(X_syn, y_syn)
clf.fit()
print(f'acc = {acc(clf.predict_label(X_syn), y_syn)}')
df = load_breast_cancer()
X_real, y_real = df['data'], df['target']
X_real = (X_real - X_real.mean(0)) / X_real.std(0)
y_real = y_real * 2 - 1
clf_real = SVM(X_real, y_real, kernel=np.dot)
clf_real.fit()
print(f'acc of breast cancer = {acc(clf_real.predict_label(X_real), y_real)}')