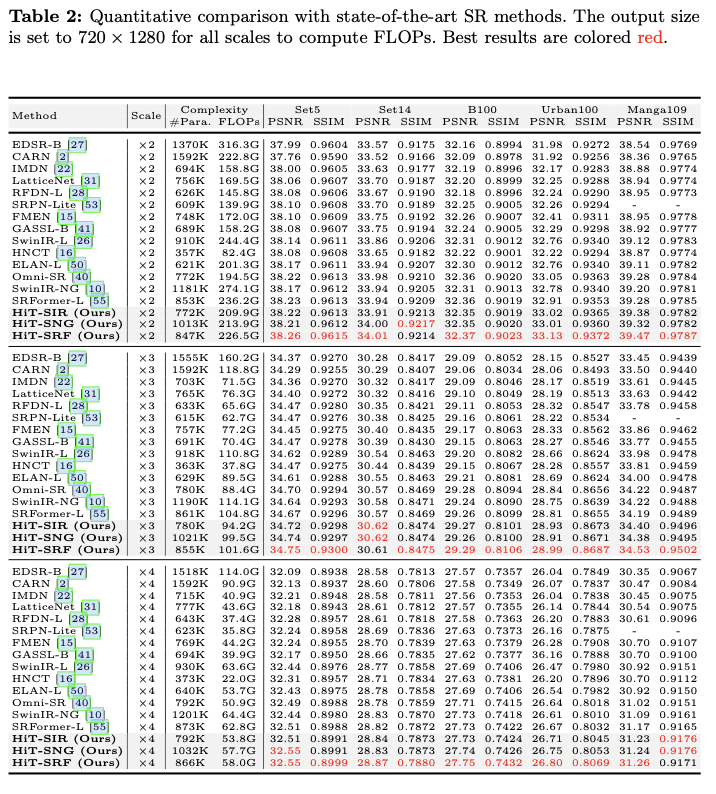
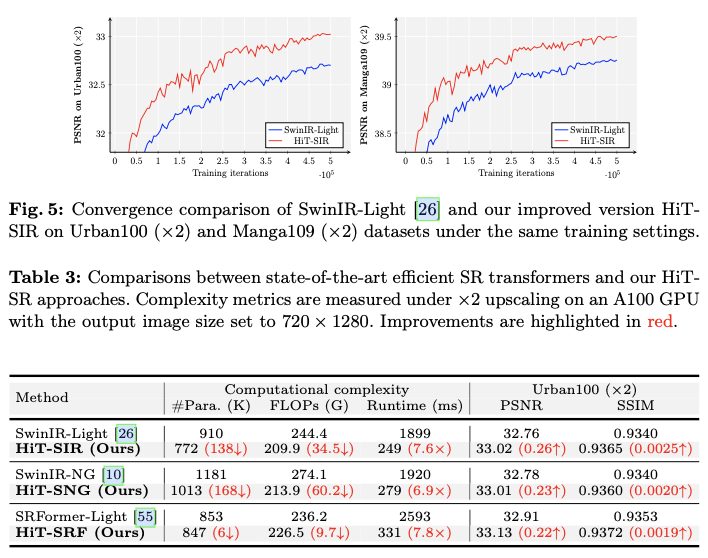
一、前言
本文介绍一下Kafka赫赫有名的组件Purgatory,相信做Kafka的朋友或多或少都对其有一定的了解,至少是听过它的名字。那它的作用是什么呢,用来解决什么问题呢?官网confluent早就有文章对其做了阐述
这里简单总结一下:Purgatory是用来存储那些处于临时或等待状态的请求,这些请求可能某些条件未被满足,而被临时管理了起来。在这些条件满足后,或者请求超时后,这些请求会被Purgatory高效回调,继而继续执行后续逻辑
这里聊个题外话,为什么Kafka要给其取名“炼狱”呢?以下可以看一下百科对其的释义
在教会的传统中,炼狱是指人死后精炼的过程,是将人身上的罪污加以净化,是一种人经过死亡而达到圆满的境界(天堂)过程中被净炼的体验
相信Purgatory在这里更强调的是临时,另外还有诸如Reaper(死神)等的命名,可见Kafka原作者们还是很有文艺范的 :)
二、演化
关于Purgatory组件的形成,并不是一蹴而就的,它至少经历了2个大版本的迭代。
- 版本一:在Kafka 0.8版本及以前,使用的是第一版,这个版本的核心是严重依赖了JUC的延迟队列(
java.util.concurrent.DelayQueue
)。然而放入Purgatory中的这些延迟任务,大多数的时候,并不会真正等到时间超时。例如acks=all的这种case,假设默认的超时时间为1秒,即需要在1秒钟之内将数据同步给所有的follower,leader将数据放入Purgatory后便开始了回调等待,但大多数情况,可能几十ms数据便同步完并执行回调结束本次异步操作,然而存在于延迟队列
DelayQueue
中的请求并不能真正被删除,它只能在真正超时的时候(1秒后),才能被发现并删除。因此白白占用昂贵的内存资源是一个弊端,而且存在一些性能上的问题,对于entry的增加、修改时间复杂度也达到了log(N)
- 版本二:而在之后的版本中,Kafka对其做了优化,引入了优秀的设计 Hierarchical Timing Wheel(多层时间轮)的概念,不仅能够立即将已完成的任务删除,而且使其性能飙升,几乎达到了常量O(1)的程度,关于具体的版本演练及性能测试可以参看官网文章
不过文章中对很多细节并没有展开,也没有源码级流程的讲解,这也是本文诞生的初衷,接下来我们会对Purgatory有一个全方位的介绍,包括其设计理念及源码分析。另:源码均来自于当前社区最新的trunk分支,也就是不久后的4.0.0的release分支,考虑到Purgatory已经相当稳定成熟,因此在当前trunk分支至4.0.0并不会有大的变动
三、整体业务流程
为了对Purgatroy扮演的角色有一个全局的概念,我们以Consumer的
Join Group
来举例说明。Join Group要做的事情也非常简单,它需要协调多个Consumer在某个时间窗口内,尽量快速调用Join Group接口,在此,后续的结果分两种情况考虑
- 所有的Consumer在时间窗口内均调用了Join Group后,Coordinator开始制定分区分配策略
- 在时间窗口结束的时候,只有一部分Consumer调用了Join Group,Coordinator便将那些没有调用Join Group剔除,只对这些调用了Join Group的Consumer开始制定分配策略
假设现在没有Purgatory组件,我们实现起来的话,流程可能如下:
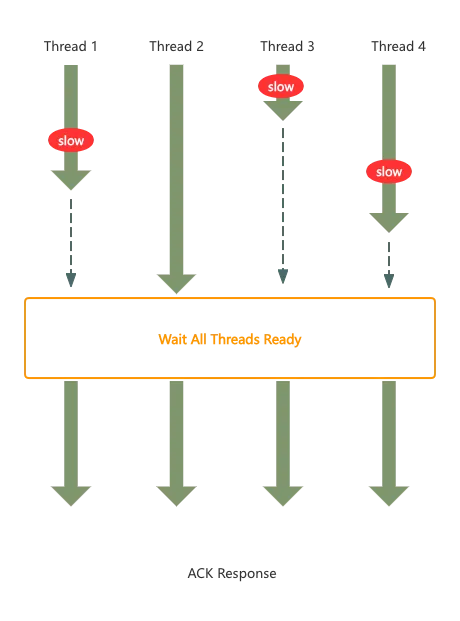
假定4个线程在时间窗口内都到达了,但是到达的前后顺序不一致。线程2已到达,线程1、线程3、线程4都还在路上,因此线程2一直处于挂起状态,即便是有新的任务到达,线程2也无法进行响应处理,且对应线程2的占用一直要等到ack response后,才能释放出来,
效率低下
而图中“Wait All Threads Ready”组件如何实现呢?其实可以使用JDK的CyclicBarrier或Semaphore或CountDownLatch均可实现,但不是本文要讨论的重点,不再展开
Purgatory如何实现呢?它在整个流程中扮演了一个什么角色呢
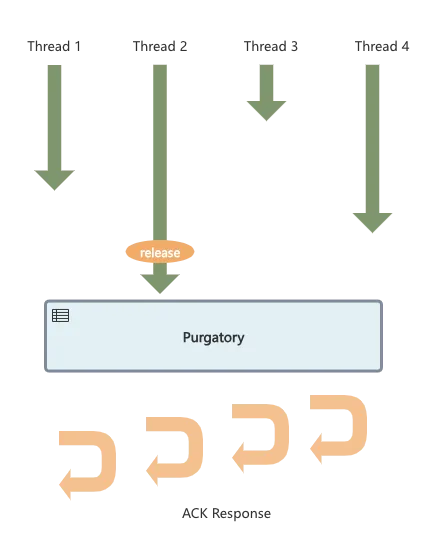
首先流程上还是4个线程先后过来调用接口,但区别在于,已经到达的线程只需要将自己已经receive的消息(包含回调、超时等基础数据)给到Purgatory即可,而后这个线程将会被释放,它可以去处理其他任务。而后续的操作则会由Purgatory来接管,包括判断条件是否满足、窗口是否超时,一旦其中一个条件满足,Purgatory将执行回调,挨个对这些请求进行ack response
知道了Purgatory在整体流程中扮演的角色,接下来我们就要对这个组件内部实现的细节进行展开了
四、Purgatory组成
我们还是先提供一张Purgatory运作的流程图
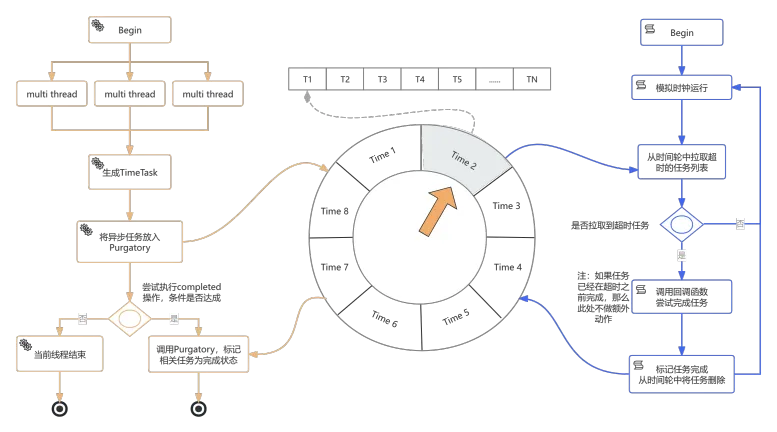
4.1、业务线程
业务线程,对应上图左侧部分的流程。所谓业务线程,即使用Purgatory组件作为暂存请求的线程,例如Join Group、Producer ACKS=all等,虽然业务线程调用Purgatory的代码非常简单,只有一行,拿Join Group举例:
rebalancePurgatory.tryCompleteElseWatch(delayedRebalance, Seq(groupKey))
但在Purgatory内部却做了很多事儿:
- 首先尝试去完成调用,如果所有条件均已满足,那么当前任务直接成功,也就不需要与时间轮交互了
- 如果条件不满足,则会将任务存储在时间轮
- 如果用户设置了key,同时还会对同key的TimeTask进行监听
- 其实就是对同key的任务做批量操作,比如一起取消,后文还会提及
可见业务线程只负责向时间轮中写入数据,那时间轮中的数据什么时候被清除呢?这就要涉及另外一个核心线程ExpiredOperationReaper
4.2、收割线程
在Purgatory的内部还存在一个独立的线程ExpiredOperationReaper,我们可以将其翻译为收割线程或清理线程,它的作用是实时扫描那些已经过期的任务,并将其从时间轮中移除。它的定义如下
/**
* A background reaper to expire delayed operations that have timed out
*/
private class ExpiredOperationReaper extends ShutdownableThread(
"ExpirationReaper-%d-%s".format(brokerId, purgatoryName),
false) {
override def doWork(): Unit = {
advanceClock(200L)
}
}
这里需要注意的是,收割线程只是一个独立的单线程,它的作用只是去实时找出那些已经过期的任务,并将后续的回调逻辑扔给线程池,继而继续扫描,由此可见其任务并不繁重
这里简单提一下“回调线程池”,由上文我们知道线程将任务交给Purgatory后便结束使命了,后续的触发均有这个“回调线程池”中的线程来执行的,这个线程池定义如下
this.taskExecutor = Executors.newFixedThreadPool(1,
runnable -> KafkaThread.nonDaemon(SYSTEM_TIMER_THREAD_PREFIX + executorName, runnable));
可见它是一个单线程的,且固定线程数的线程池。为什么要设置为单线程呢?如果某个应用的回调阻塞了,那岂不是所有线程池中的回调均会阻塞吗?
的确是这样,不过考虑到这个线程池做的工作只是回调,一般是网络发送模块,数据其实都是已经准备好的,TPS响应是非常快的,因此通常也不会成为瓶颈
由上文可知,不论是业务线程还是收割线程,其与时间轮均有密不可分的关系
五、时间轮(Timing Wheel)
不论是延迟任务的管理、存储、移除等核心操作,均是由时间轮来完成,因此时间轮是整个Purgatory中的最核心组件。此处我们再明确一下Purgatory与时间轮的关系,时间轮只是Purgatory中的一个子概念,是为了让Purgatory更高效、性能更快而提炼出的一个内部组件
5.1、数据结构
时间轮的数据结构也相对简单,由一个轮子+双向链表组成
轮子:
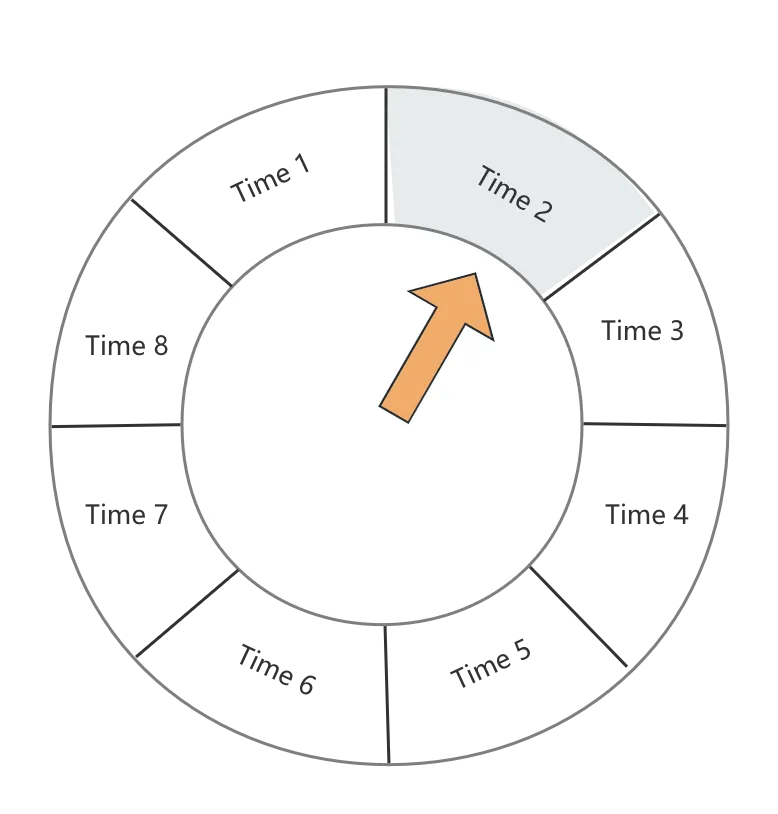
双向列表:

轮子+双向列表的结构便为:
之所以设计双向链表的方式,主要是Task的新增跟删除是一件非常频繁的事儿,我们的数据结构要能确保高效地处理这些请求,而双向循环链表则能够保证任意一个Task节点的新增与删除都能维持O(1)的时间复杂度,因此可谓是不二之选
5.2、Task添加与移除
具体的Task添加与删除的过程是什么样呢?我们举个例子来说明:
假定我现在时间轮的粒度为10秒钟,即每10秒一个格子
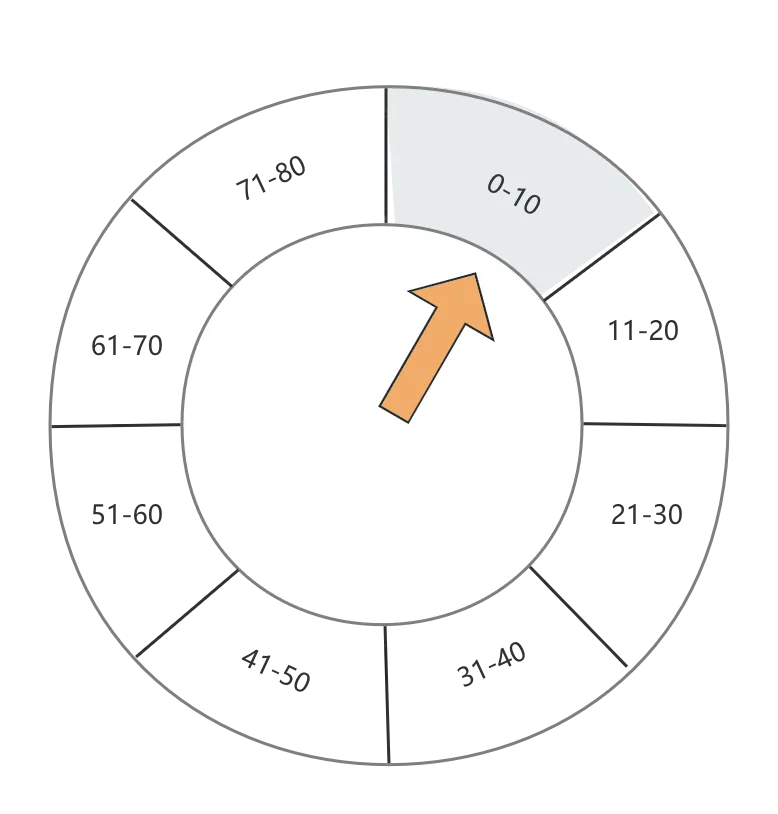
现在来了一个任务,这个任务Task1要在第35秒被触发,此时我们找到第4个时间格,将这个任务放在这里
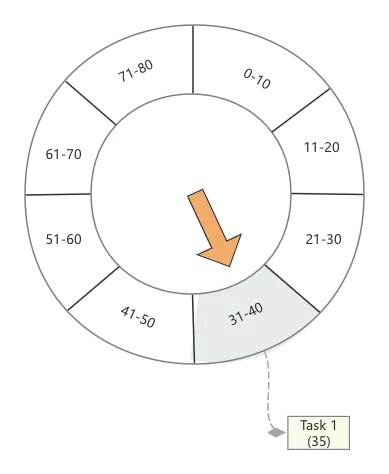
接着又来了2个任务,分别在36、38秒被触发,那么同样它们将会被放在第4个时间格中
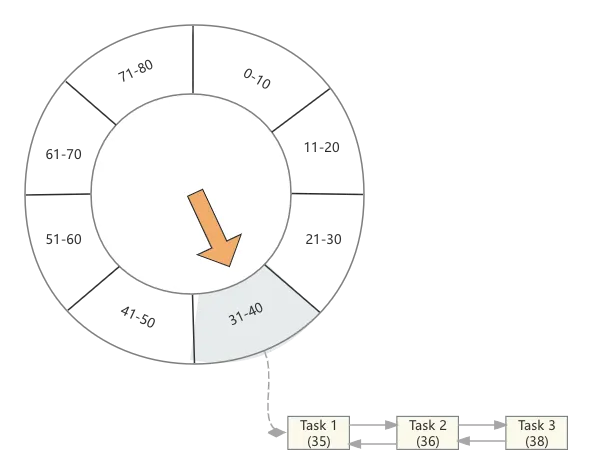
同理,不难想象,如果又来了几个任务,它们的触发时间分别为12、18、69、62、65、53、54,那么时间轮将会变为如下
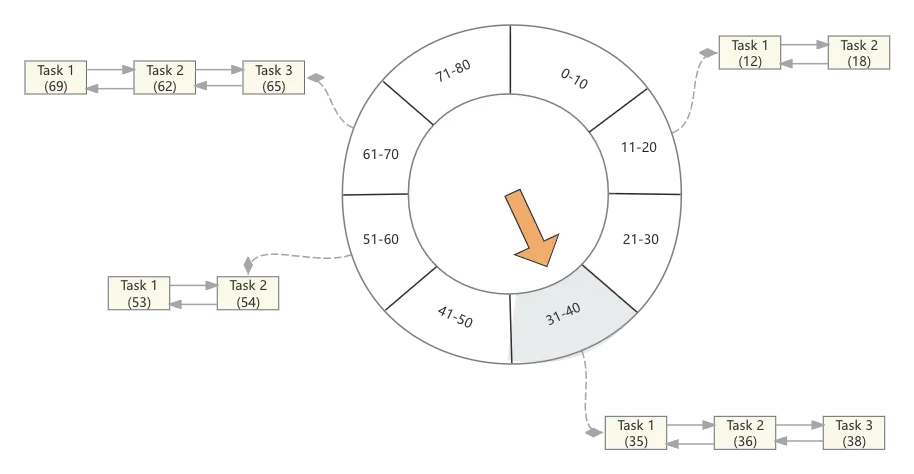
如果来个延迟时间是100秒的任务呢?其实这块就涉及到多级时间轮了
至于任务的移除,参照双向链表删除节点即可
5.3、多级时间轮
5.3.1、基础定义
多级时间轮,顾名思义,即有很多个层级的时间轮,越往上,粒度越粗,理论上只要内存够大,时间轮可以存储无限大小的延迟任务。下图展示了一个2级时间轮:
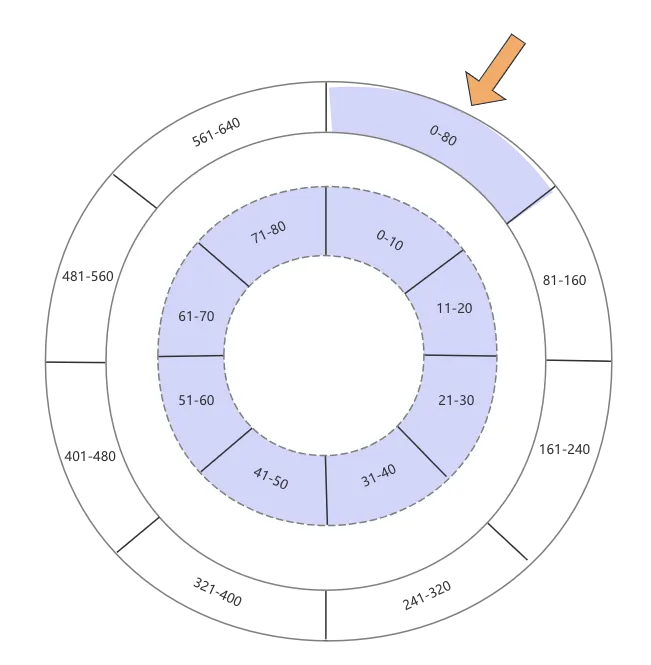
- 内层时间轮:时间粒度是10秒钟,每个时间轮有8个格子,因此内层的时间轮可以存储0-80秒的任务
- 外层时间轮:时间粒度是80秒钟,同样也是有8个格子,外层的时间轮则可以存储0-640秒的任务
其实每个外层时间轮的一个格子,均对应一个内层时间轮,只不过上图没有呈现出这一点,因此,接上文,如果我们要存储一个100秒的任务时,当前时间轮发现越界了,它会无脑向上抛,直到找到能接住这个超时时间的时间轮,上层时间轮的跨度更大,因此100秒的任务会落在“81-160”这个格子上。虽然更上层的时间轮承接了这个任务,但其实处理这个任务的最终还将会是最细粒度的时间轮,也就是将来在“81-160”这个格子对应的内层时间轮会最终接受这个任务并触发回调,这点我们在“时钟模拟”章节再展开
因此其实我们不用在意到底Purgatory会有多少个层级的时间轮,理论上它可能是无限大的,我们只需要知道最细粒度的时间轮的步长+个数,后面的轮子构成都可以推导出来。那Kafka设定的最细粒度的轮子步长跟个数分别是多少呢?这个答案藏在org.apache.kafka.server.util.timer.SystemTimer类的构造方法中
public SystemTimer(String executorName) {
this(executorName, 1, 20, Time.SYSTEM.hiResClockMs());
}
可见,最细粒度的时间步长为1ms,个数为20,由此可推导出一个表格
层级 |
步长 |
个数 |
最长时间 |
1 |
1ms |
20 |
20ms |
2 |
20ms |
20 |
400ms |
3 |
400ms |
20 |
8s |
4 |
8s |
20 |
160s (2分40秒) |
5 |
160s |
20 |
3200s (53分20秒) |
6 |
3200s |
20 |
64000s (17时46分40秒) |
可见到了第6层,延时时长已经到达了17个小时,而Kafka一般的case,可能到第4层就足矣;而从整体看,时间轮最细粒度精确到了1ms,且可以接收理论上无限长的定时任务,真可谓是神器了。不过这里也存有一点疑问,那就是粒度做的这么细,性能方面是不是存在问题?这点我们在后文也会涉及
5.3.2、Task添加
这节梳理一下在多级时间轮下,Task的添加与移除操作,关于Task的添加,一言以蔽之就是如果目标Task超过当前时间轮的最大时间范围,那么直接抛给上级时间轮;还是那上文举个例子,假如时间轮收到一个700秒后执行的延迟任务
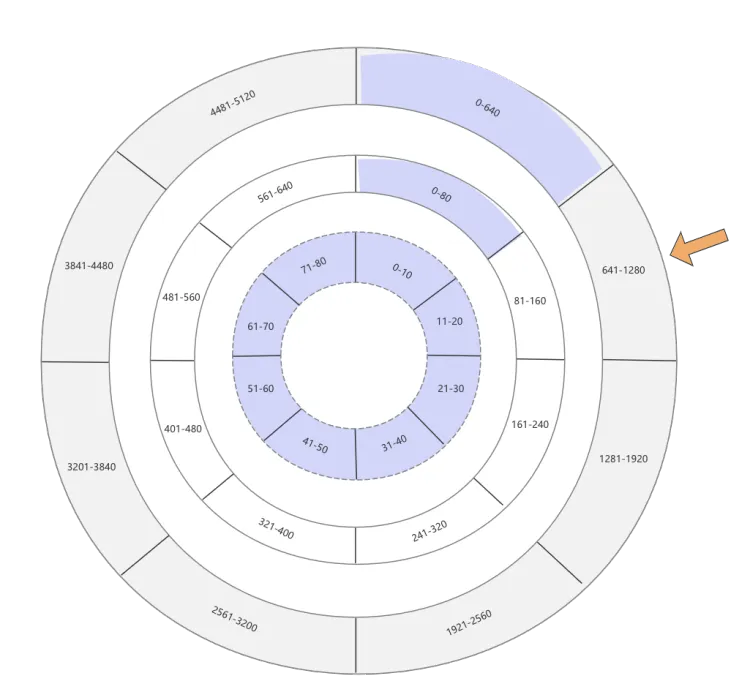
一级时间轮,也就是最细粒度的时间轮,范围是0-80秒,无法存放,那么向上抛送;
二级时间轮收到这个任务后,发现超时时间是700秒,而自己的范围则是0-640,依旧无法存放,继续向上抛送
三级时间轮收到任务后依然检查自己能接收的时间范围,发现是0-5120秒,700秒在自己的范围内,继而计算700秒任务应该落在哪个格子,最终其被存放在641-1280这个格子中
总结:任务的添加总是先交给最细粒度的时间轮,而后层层上报,直到找到能承接这个Task的轮子后便将其存放在对应的格子中
5.3.2、Task移除
常规情况下,一个处于高Level的Task,在还没有真正过期时,它的移除动作就是将其放入更细粒度的时间轮中,还是以上图中的例子来说明
- 现在700秒的Task被放在三级时间轮的"641-1280"这个格子(TaskList)中,这个格子将在640秒过期
- 现在时钟刚过640秒,"641-1280"这个格子被推出,发现其中有1个700秒超时的任务,但是其还没有真正超时,因为当前的时间是640秒
- 而后这个任务将会被重新加入时间轮,因为时钟已经过了640秒,因此此时的一级、二级时间轮均发生了变化,二级时间轮被替换为如下,因此当前任务会被放入641-720格子中
- 641-720
- 721-800
- 801-880
- 881-960
- 961-1040
- 1041-1120
- 1121-1200
- 1201-1280
- 而641-720格子对应的一级时间轮如下,700秒任务对应的格子为691-700,因此在后续的时钟模拟中,真正要等到691-700这个格子被唤醒才能调用
- 641-650
- 651-660
- 661-670
- 671-680
- 681-690
- 691-700
- 701-710
- 711-720
5.4、时钟模拟
接下来就是非常重要的一步,Purgatory要模拟时钟往前推进时间,从而触发相关任务被唤醒
5.4.1、java.util.concurrent.DelayQueue
在真正开始介绍时钟模拟前,我们需要先铺垫一个关键的JUC包下的类java.util.concurrent.DelayQueue,整个时钟模拟在很大程度上依赖这个延迟队列的能力。DelayQueue有如下几个核心方法:
- put (java.util.concurrent.Delayed delayed) 将一个延迟对象放入延迟队列中
- offer (java.util.concurrent.Delayed delayed) 同 put
- poll() 将会一直阻塞, 直到返回一个已经过期的延迟对象,不过如果当前的延迟队列中没有数据,将会直接返回null
- poll(long timeout, TimeUnit unit) 功能与poll() 相似,只不过当前方法加入了超时限定,且如果延迟队列为空的话,也不会立即返回null,而是等待超时
因为DelayQueue只接受java.util.concurrent.Delayed对象,此对象的定义如下
/**
* A mix-in style interface for marking objects that should be
* acted upon after a given delay.
*
* <p>An implementation of this interface must define a
* {@code compareTo} method that provides an ordering consistent with
* its {@code getDelay} method.
*
* @since 1.5
* @author Doug Lea
*/
public interface Delayed extends Comparable<Delayed> {
/**
* Returns the remaining delay associated with this object, in the
* given time unit.
*
* @param unit the time unit
* @return the remaining delay; zero or negative values indicate
* that the delay has already elapsed
*/
long getDelay(TimeUnit unit);
}
可见是一个接口,如果使用的话,我们需要定义一个延迟类,并实现这个接口。我们可以写一个延迟队列的小例子来个直观感受
public class DelayedQueueExample {
public static void main(String[] args) throws InterruptedException {
DelayQueue<DelayedItem> delayQueue = new DelayQueue<>();
delayQueue.put(new DelayedItem(2000));
delayQueue.put(new DelayedItem(5000));
delayQueue.offer(new DelayedItem(6000));
while (!delayQueue.isEmpty()) {
DelayedItem delayedItem = delayQueue.poll(200, TimeUnit.MILLISECONDS);
if (delayedItem != null) {
System.out.println("delayedItem content : " + delayedItem);
} else {
System.out.println("DelayedItem is null");
}
}
}
private static class DelayedItem implements Delayed {
private final long expirationTime;
public DelayedItem(long delayTime) {
this.expirationTime = System.currentTimeMillis() + delayTime;
}
@Override
public long getDelay(TimeUnit unit) {
long diff = expirationTime - System.currentTimeMillis();
return unit.convert(diff, TimeUnit.MILLISECONDS);
}
@Override
public int compareTo(Delayed other) {
if (this.getDelay(TimeUnit.MILLISECONDS) < other.getDelay(TimeUnit.MILLISECONDS)) {
return -1;
}
if (this.getDelay(TimeUnit.MILLISECONDS) > other.getDelay(TimeUnit.MILLISECONDS)) {
return 1;
}
return 0;
}
}
}
上述例子中,我们往延迟队列中放入了3条数据,它们需要处理延迟请求的时间分别是2秒、5秒、6秒,当调用poll()方法时,可以精确在对应的时间收到该请求的回调,当然这块的高效得益于Doug Lea大神的JUC包
有同学可能会说,既然JUC的延迟队列都能把这些事儿做了,还要时间轮做什么用呢?自然延迟队列是有它自己问题的,参看“演化”模块
5.4.2、延迟对象
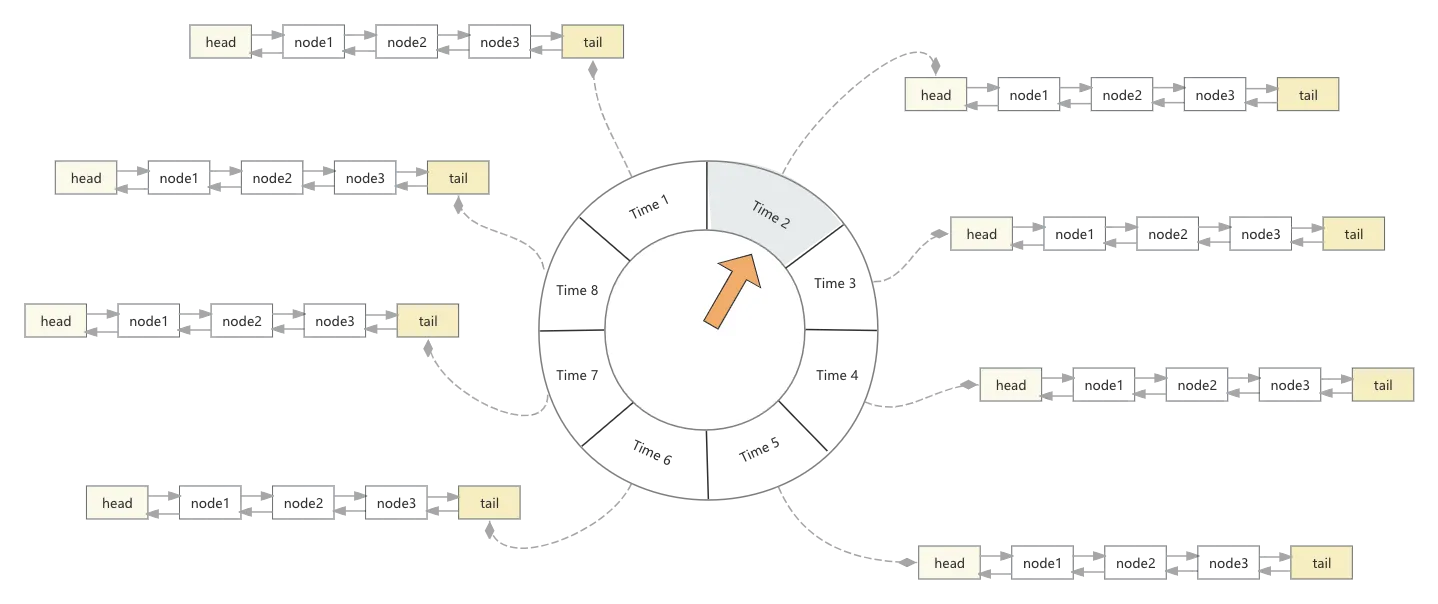
那放入延迟队列java.util.concurrent.DelayQueue的元素是这些延迟Task吗?答案是否定的,因为这些任务一旦放入延迟队列,那它的删除就会成为负担,而且带来大量内存的占用(其实Purgatory的第一版就是这样设计的),其实这里延迟队列的元素是时间轮中的双向循环列表,如下图
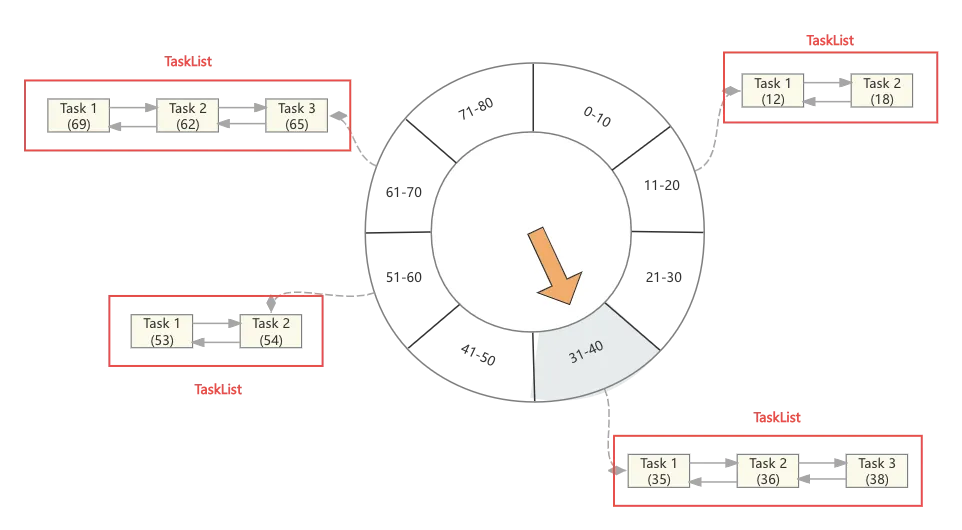
这里关于任务的添加与删除,站在延迟队列的角度再讨论一下
- 当Task加入到时间轮中的一个空格子中时,此时会创建一个TaskList对象,当然这个TaskList的双向链表中只有一个元素,而后这个TaskList被加入延迟队列
- 当Task加入一个有数据的格子中时,直接将这个Task加入TaskList的链表中,因为这个TaskList已经托付给延迟队列管理,因此此时不涉及延迟队列操作
- 当某个Task需要删除时,直接找到对应的TaskList,将其从链表中移除
- 当TaskList超时,被延迟队列唤起,此时这些Task将会被依次处理,而如果TaskList中的链表为空,则直接跳过
这样不仅完美避开了对延迟队列中元素删除的操作,而且完美解决了OOM的问题,且元素的新增、删除时间复杂度均为O(1)
5.4.3、Tick
模拟时钟推进使用的线程即为上文提到的收割线程,方法的入口为
kafka.server.DelayedOperationPurgatory#advanceClock
,当然这里处理的均是已经超时的请求,因此如果所有的操作均没有超时,那收割线程实际没有需要处理的业务
其实关于Tick操作的核心就是调用延迟队列的poll操作,用来获取那些已经超时的TimerTaskList
TimerTaskList bucket = delayQueue.poll(timeoutMs, TimeUnit.MILLISECONDS);
不过这个Tick的粒度是时间轮的每一个格子,因此它与Task的频率是不一致的,通常一个格子中可能包含了多个Task,这些Task如果在时间上确实超时了,那么会真正业务回调,如果没有超时,将重新加入时间轮
5.5、Watch Key
所谓Watch Key,通常是将一组生命周期相关的数据设置同一个key,这样在条件达成后,可将这组任务统一回调,不论是成功还是取消
例如当执行Group的Join操作时,预期会有10个consumer调用Join接口,然后每个consumer调用接口时,均带上watch key参数(这里的watch key可以设置为group name),只要发现调用这个key的数量满10个后,便可以将这10个延迟请求统一回调,同时将其从时间轮中删除
六、源码分析
我们将上图关键部分标记出相关类
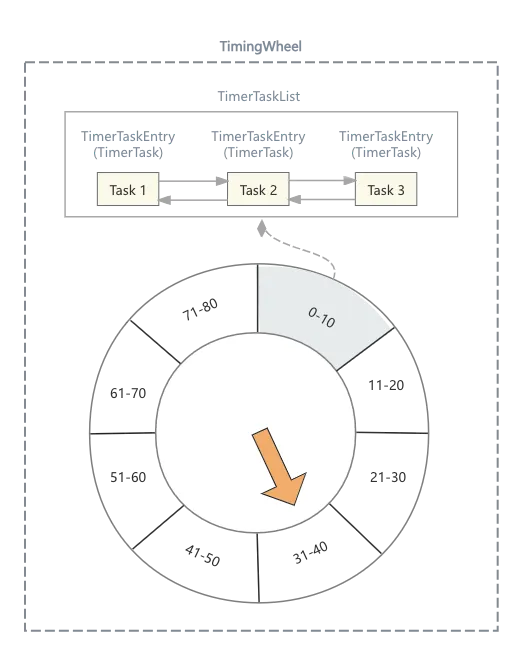
- 首先整个时间轮对应的类为
org.apache.kafka.server.util.timer.TimingWheel
- 时间轮上每个格子对应的类为
org.apache.kafka.server.util.timer.TimerTaskList
- 每个格子中链表中的元素对应的类为
org.apache.kafka.server.util.timer.TimerTaskEntry
- 每个元素中需要存储TimerTask,这个类为抽象类,也是需要用户自己去实现的
org.apache.kafka.server.util.timer.TimerTask
其实通过这张图,我们对Purgatory涉及的类便有了全貌的了解,这里主要了解的是TimerTask,因为其他类均被包装在Purgatory组件内部,不需要继承,也不涉及改动。TimerTask的定义如下
public abstract class TimerTask implements Runnable {
private volatile TimerTaskEntry timerTaskEntry;
public final long delayMs;
}
这两个属性也较好理解
- timerTaskEntry:它与TimerTask其实就是1:1的关系,同样在TimerTask中也有TimerTaskEntry的引用
- delayMs:延迟时间,也就该任务将来被触发调用的时间
然而仅仅有这个类还是不够的,还需要在一些关键操作时,对相关接口进行回调,例如onComplete、onExpiration等。因此Kafka涉及了TimerTask的子类DelayedOperation
abstract class DelayedOperation(delayMs: Long,
lockOpt: Option[Lock] = None)
extends TimerTask(delayMs) with Logging {
private val completed = new AtomicBoolean(false)
// Visible for testing
private[server] val lock: Lock = lockOpt.getOrElse(new ReentrantLock)
/*
* Force completing the delayed operation, if not already completed.
* This function can be triggered when
*
* 1. The operation has been verified to be completable inside tryComplete()
* 2. The operation has expired and hence needs to be completed right now
*
* Return true iff the operation is completed by the caller: note that
* concurrent threads can try to complete the same operation, but only
* the first thread will succeed in completing the operation and return
* true, others will still return false
*/
def forceComplete(): Boolean = {
if (completed.compareAndSet(false, true)) {
// cancel the timeout timer
cancel()
onComplete()
true
} else {
false
}
}
/**
* Check if the delayed operation is already completed
*/
def isCompleted: Boolean = completed.get()
/**
* Call-back to execute when a delayed operation gets expired and hence forced to complete.
*/
def onExpiration(): Unit
/**
* Process for completing an operation; This function needs to be defined
* in subclasses and will be called exactly once in forceComplete()
*/
def onComplete(): Unit
/**
* Try to complete the delayed operation by first checking if the operation
* can be completed by now. If yes execute the completion logic by calling
* forceComplete() and return true iff forceComplete returns true; otherwise return false
*
* This function needs to be defined in subclasses
*/
def tryComplete(): Boolean
/**
* Thread-safe variant of tryComplete() and call extra function if first tryComplete returns false
* @param f else function to be executed after first tryComplete returns false
* @return result of tryComplete
*/
private[server] def safeTryCompleteOrElse(f: => Unit): Boolean = inLock(lock) {
if (tryComplete()) true
else {
f
// last completion check
tryComplete()
}
}
/**
* Thread-safe variant of tryComplete()
*/
private[server] def safeTryComplete(): Boolean = inLock(lock)(tryComplete())
/*
* run() method defines a task that is executed on timeout
*/
override def run(): Unit = {
if (forceComplete())
onExpiration()
}
}
所有的业务类均需要继承DelayedOperation并重写相关方法,相关逻辑不再赘述
总结:以上只是分析了Purgatory的设计思路及大致流程,还有很多多线程并发相关的性能操作,Kafka均处理的非常漂亮,本文不能枚举,读者有兴趣可以参照文章过一遍源码,相信大有裨益