来源：晓飞的算法工程笔记 公众号，转载请注明出处

论文: Straightforward Layer-wise Pruning for More Efficient Visual Adaptation

创新点

  • 提出了一种针对
    PETL
    模型的剪枝方法
    SLS
    （
    Straightforward Layer-wiSe Pruning method
    ），证明在下游数据集与预训练数据集之间存在显著差距时，
    PETL
    转移后的模型中存在大量冗余参数。
  • 提出了一种直观的特征级分析方法，为评估结构剪枝参数的重要性提供了一种新的视角。
  • SLS
    在
    VTAB-1k
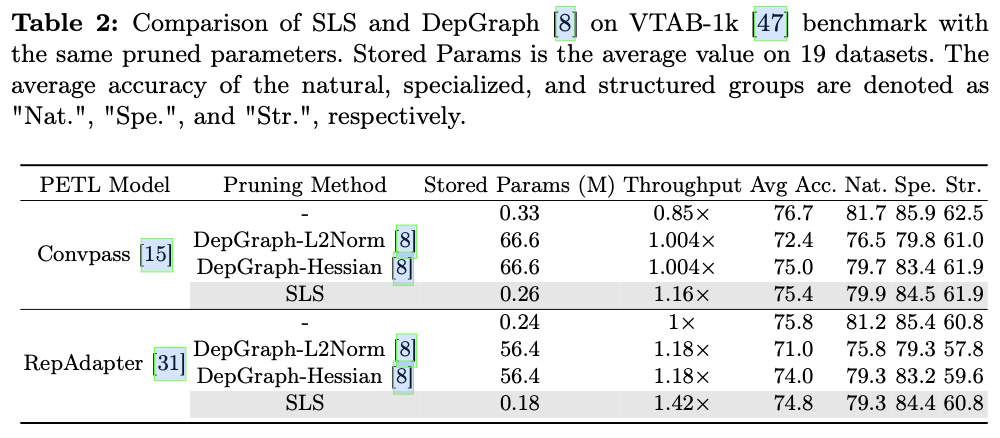
    基准测试中，使用相同的剪枝参数数量，以简单的策略在模型存储、准确性和速度上超越了当前主流的结构剪枝方法
    DepGraph
    。

内容概述

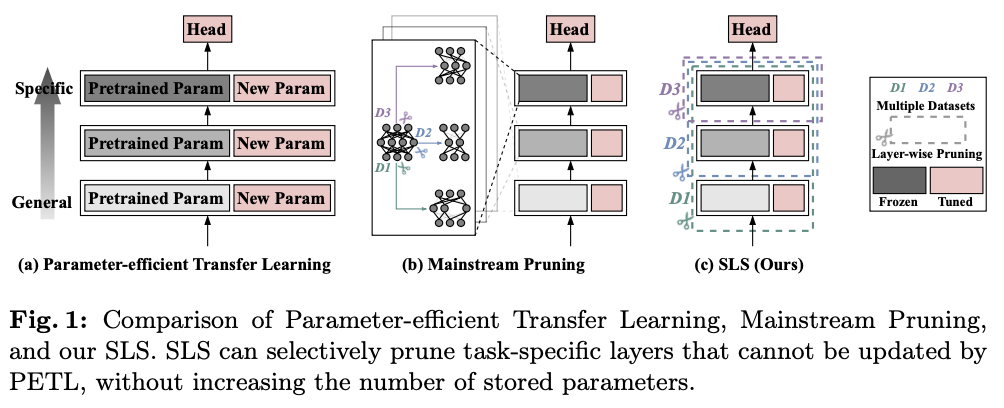
参数高效迁移学习（
PETL
）旨在使用有限的参数调整大型预训练模型。虽然大多数
PETL
方法在训练过程中仅更新添加或选择的参数并冻结预训练权重，但因为
PETL
难以回传梯度调整顶层的参数，往往会导致冗余的模型结构。结构剪枝有效降低了模型冗余，但常见的剪枝方法通常会导致存储参数的过度增加，因为不同剪枝率和数据会产生不同的剪枝结构。

针对存储参数量的问题，论文提出了一种直接的层级剪枝方法
SLS
（
Straightforward Layer-wiSe Pruning method
），用于剪枝
PETL
模型。
SLS
通过从特征角度评估每一层的参数，并利用聚类度量通过
t-SNE
获得的低维空间中的聚类现象来评估当前层参数，
SLS
促进了基于信息的剪枝决策。逐层剪枝专注于存储剪枝索引，解决了存储量的问题。

值得注意的是，主流的逐层剪枝方法可能不适合评估
PETL
转移模型中层的重要性，因为大多数参数是预训练的，并且与下游数据集的相关性有限。与最先进的
PETL
方法进行的比较分析表明，剪枝模型在模型吞吐量和准确性之间实现了显著的平衡。此外，
SLS
有效减少了由于不同剪枝结构而产生的存储开销，同时在与传统剪枝方法相比时提升了剪枝模型的准确性和速度。

SLS

以往的研究表明，较低层通常捕捉一般特征，而较高层则专注于特定特征。基于这一理解以及在
PETL
模型中冻结预训练网络参数的局限性，论文认为当下游数据分布与预训练数据分布之间存在显著差异时，
PETL
转移的模型深层将包含大量冗余参数。于是论文打算动态识别并剪除这些冗余参数。为了确保剪枝过程的有效性，必须满足以下关键标准：

  1. 保持与
    PETL
    转移方法相同的存储参数数量。

  2. 预测冗余参数而无需额外的训练。

相关算法

  • 降维算法
    t-SNE
    ：给定一组
    \(d\)
    维输入特征
    \(X=\{x_1,x_2,...,x_n\}\in \mathbb{R}^{n\times d}\)
    ，为
    \(X\)
    计算一组
    \(s\)
    维嵌入，记作
    \(Y=\{y_1,y_2,...,y_n\}\in \mathbb{R}^{n\times s}\)
    。其中
    \(s\ll d\)
    ，通常为
    2
    或
    3
    以便于可视化。首先使用联合概率来度量输入
    \(X\)
    中
    \(x_i\)
    和
    \(x_j\)
    之间的相似性，随后调整随机初始化
    \(Y\)
    ，使
    \(Y\)
    元素之间的相似性与
    \(X\)
    对应元素之间的相似性一致。

  • 聚类算法指标
    SC_Index
    (
    Silhouette Coefficient Index
    )：给定一组聚类结果
    \(X=\{x_1,x_2,...,x_n\}\)
    ，对于某一点
    \(x_i\)
    ，定义
    \(a(i)\)
    为其所在聚类中剩余点与
    \(x_i\)
    之间的平均距离，
    \(b(i)\)
    为
    \(x_i\)
    与最近聚类中所有点之间的平均距离。


    \[\begin{equation}
    \bar{s}=\frac{1}{n}\sum_{i=1}^n\frac{b(i)-a(i)}{\max(a(i),b(i))}
    \end{equation}
    \]

层级剪枝不会增加存储参数数量

SLS
的预测不涉及额外的参数引用，采用基于现有特征的聚类方法预测剪枝层索引表示为
\(Index_j\)
直接进行剪枝。因此，通过
SLS
剪枝的模型不会产生任何额外的存储开销。

根据各层的中间特征做出剪枝决定

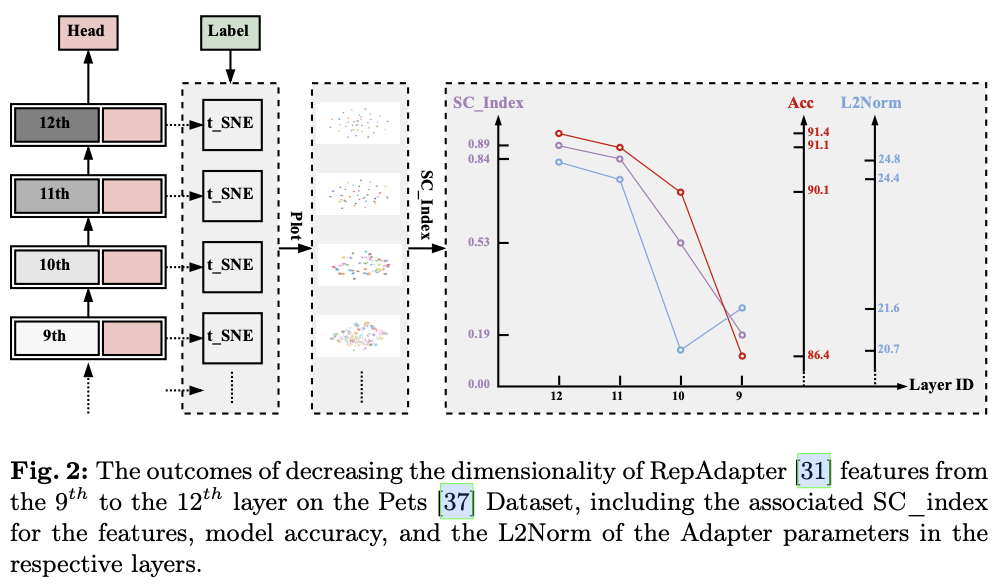
使用降维特征的聚类程度
SC_Index
来评估层特征，该方法不引入额外的监督训练。如图
2
所示，在适当的设置下，模型中当前层的分类准确率与降维特征的
SC_Index
之间存在明显的相关性。

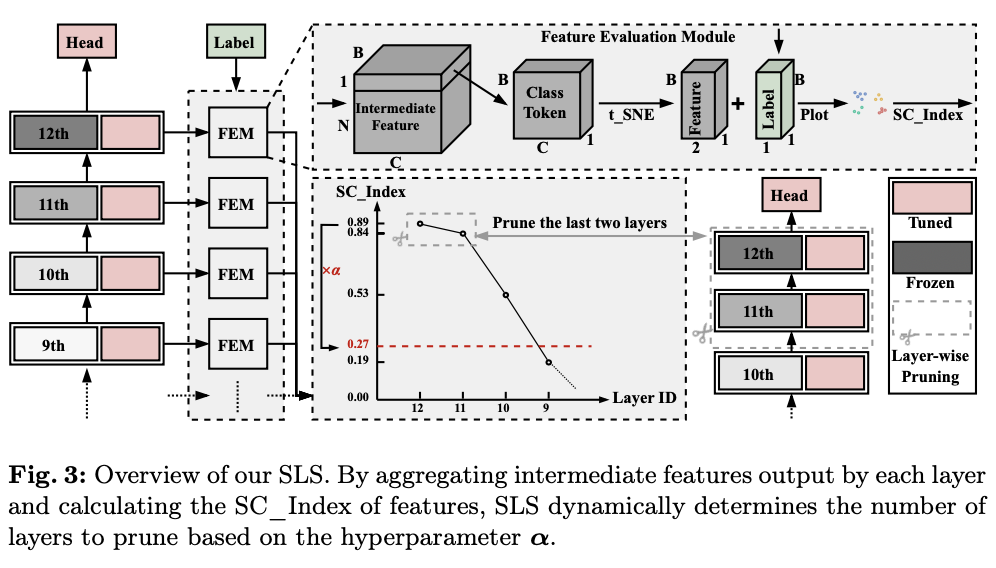
论文提出了特征评估模块 (
FEM
) 来评估来自层
\(L_i\)
的特征。如图
3
所示，
FEM
从层
\(L_i\)
的输出
\([x_i,e_i]\)
中提取
cls_token
\(x_i\)
来表示当前特征，使用
t-SNE
算法将
\(x_i\)
降维到
\(x_i' \in \mathbb{R}^{B\times2}\)
。随后，通过结合对应于当前输入的标签
\(\in \mathbb{R}^{B\times1}\)
，得到一个具有
\(p\)
个类别的聚类结果
\(C\)
，其中
\(p\)
是当前数据集中的类别数量。最后，计算与
\(C\)
对应的值
\(a(i)\)
和
\(b(i)\)
，确定当前层特征的评估值
\(SC\_index_i\)
。

对于一个具有
\(N\)
层的模型，设
\(\mathbf{\alpha}\)
为一个超参数，控制
SLS
剪枝的程度。当前数据集上剪枝层数的阈值
\(T\)
定义为

\[\begin{equation}
\label{eq11}
T=\mathbf{\alpha} \times SC\_Index_N
\end{equation}
\]

在模型的剪枝过程中，从最高层向下遍历。当第
\(i^{th}\)
层特征的评估值
\(SC\_Index_i\)
低于阈值
\(T\)
时，停止遍历循环，并剪掉从
\(i+2\)
到
\(N\)
的层。这一设计的动机在于，当第
\(i^{th}\)
层特征的评估值低于与顶部层特征评估相比的某个阈值时，分类头将无法有效地区分当前特征。因此，
\({i+1}^{th}\)
层的输出特征是分类头能够很好地区分的最低层，剪掉从
\(i+1\)
向下的层会对模型的性能产生显著影响。

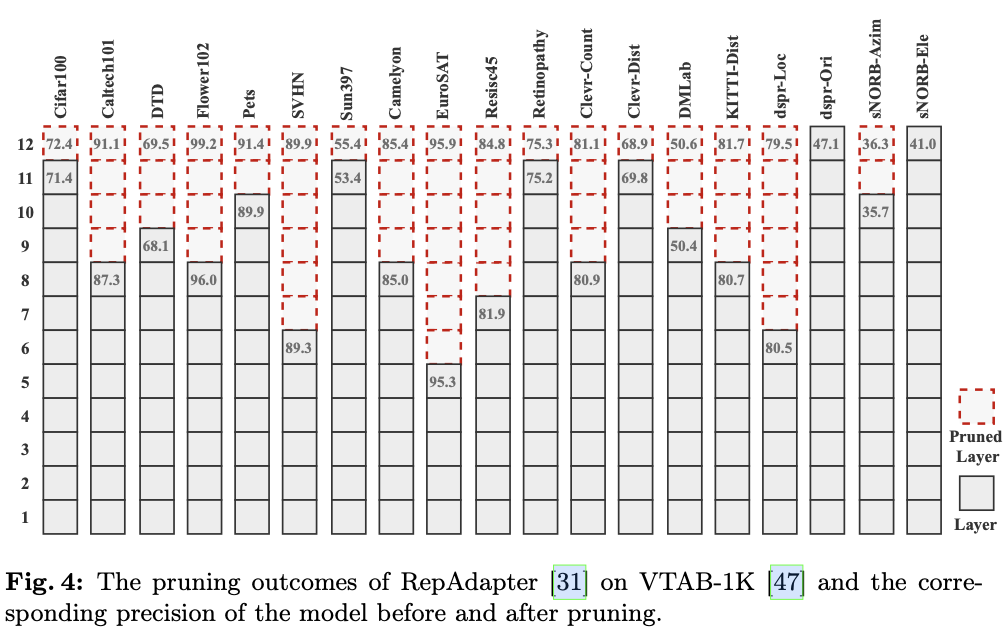
主要实验结果



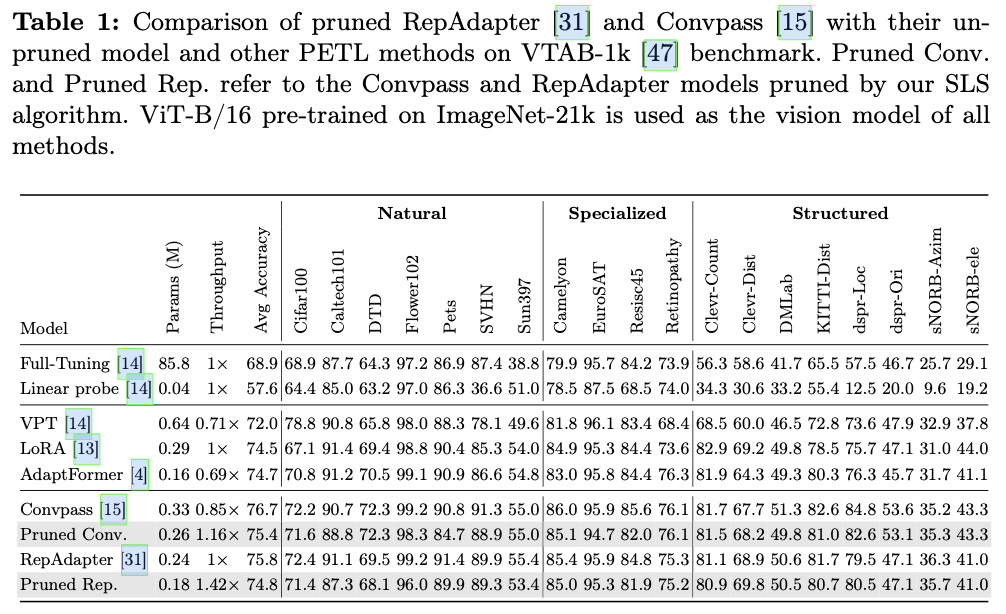
如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】

work-life balance.

标签: none

添加新评论